Динамическое программирование представляет собой математический аппарат, разработанный для решения некоторого класса задач математического программирования путем их разложения на относительно небольшие и, следовательно, менее сложные задачи. Специфика метода динамического программирования состоит в том, что для отыскания оптимального управления планируемая операция разделяется на ряд последовательных шагов или этапов. Соответственно и сам процесс планирования операции становится многошаговым и развивается последовательно, от этапа к этапу, причем каждый раз оптимизируется управление только на одном шаге. Динамическое программирование — это планирование дальновидное, с учетом перспективы
Некоторые операции естественно распадаются на этапы, в других это деление приходится вводить искусственно. Примером «естественно многоэтапной» операции может служить планирование работы предприятия на некоторый период времени, состоящий из нескольких хозяйственных лет или кварталов.
Динамическое программирование — это вычислительный метод для решения задач управления определенной структуры, когда задача с переменными представляется как многошаговый процесс принятия решений и на каждом шаге определяется экстремум функции только от одной переменной. n
Знакомство с методом динамического программирования
Процесс динамического программирования разворачивается от конца к началу. Сначала делаются различные предположения о том, чем кончился предпоследний шаг, и для каждого из них выбирается управление на последнем. Затем делаются различные предположения о том, чем кончился предпредпоследний шаг, т. е. рассматриваются различные состояния системы на третьем от конца шаге и выбирается управление на втором от концы шаге так, чтобы оно вместе в уже выбранным управлением на последнем шаге обеспечивало наилучший эффект на двух последних шагах, и так далее, вплоть до первого от начала шага, с которого начинался процесс.
Принцип искать всегда оптимальное продолжение процесса относительно того состояния, которое достигнуто в данный момент, принято называть принципом оптимальности.
Состояние на каждом шаге характ-ся некоторой переменной величиной, кот. называется параметром состояния. Наилучший эффект на данном этапе вместе с уже рассмотренными шагами хар-ся функцией состояния. Решение конкретной задачи методом динамич. программирования сводится к выбору параметра состояния, составлению ф-ии состояния и рекурентных соотношений, связывающих ф-ии состояния для двух соседних последовательных этапов, и их применению для выбора оптимального управления.
18. Матричные игры с нулевой суммой, смысл коэффициентов платежной матрицы, примеры матричных игр.
В экономике и управлении часто встречаются ситуации, в которых сталкиваются две или более стороны, преследующие различные цели, причем результат, полученный каждой из сторон при реализации определенной стратегии зависит от действий других сторон. Такие ситуации называются конфликтными. Например: аукцион, спортивные состязания, парламентские выборы (при наличии нескольких кандидатов), карточная игра.
Рассмотрим конфликт двух участников с противоположными интересами. Математической моделью такого конфликта является игра с нулевой суммой. Участники игры называются игроками. Стратегией игрока называется осознанный выбор одного из множества возможных вариантов его действий.
Рассмотрим конечные игры, в которых множества стратегий игроков конечны; стратегии первого игрока пронумеруем от 1 до m, а стратегии второго игрока — от 1 до n.
Если первый игрок выбрал свою i -ю стратегию, а второй игрок — свою j -ю стратегию, то результатом такого совместного выбора будет платеж второго игрока первому. Таким образом, игра с нулевой суммой однозначно определяется матрицей, которая называется платежной. Строки этой матрицы соответствуют стратегиям первого игрока, а столбцы — стратегиям второго игрока.
Игра происходит партиями. Партия игры состоит в том, что игроки одновременно называют свой выбор: первый игрок называет некторый номер строки матрицы, а второй — некоторый номер столбца этой матрицы. После этого происходит «расплата». Пусть, например, первый игрок назвал номер i, а второй — j. Тогда второй игрок платит первому сумму. На этом партия игры заканчивается. Если aij>0, то это означает, что при выборе первым игроком i -й стратегии, а вторым — j -й стратегии выигрывает первый игрок.
Цель каждого игрока — выиграть как можно большую сумму в результате большого числа партий. Стратегия называется чистой, если выбор игрока неизменен от партии к партии.
При любой стратегии первого игрока, второй игрок будет выбирать стратегию обеспечивающий ему наибольший выигрыш, поэтому с точки зрения первого игрока надо выбирать такую стратегию, при которой второй игрок, действуя разумно заплатит наибольшую сумму. Такая стратегия первого игрока называется максиминной, а величина  =max min aij называется нижней ценой игры.
=max min aij называется нижней ценой игры.
Аналогично (с точки зрения второго игрока) определяется верхняя цена игры 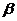 = min max a ij и соответствующая ей минимаксная стратегия второго игрока. То есть, принимая свою минимаксную стратегию второй игрок проиграет не больше
= min max a ij и соответствующая ей минимаксная стратегия второго игрока. То есть, принимая свою минимаксную стратегию второй игрок проиграет не больше  .
.
В общем случае имеет место неравенство α≤β, если же α=β, то говорят, что игра имеет седловую точку, общее значение и β называется при этом ценой игры.
При этом стратегии игроков, соответствующие седловой точке, называются оптимальными чистыми стратегиями, так как эти стратегии являются наиболее выгодными сразу для обоих игроков.
Смешанной стратегией первого игрока называется вектор 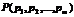 , где все
, где все 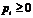 , а
, а  . При этом
. При этом 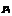 — вероятность, с которой первый игрок выбирает свою i -ю стратегию. Аналогично определяются смешанные стратегии
— вероятность, с которой первый игрок выбирает свою i -ю стратегию. Аналогично определяются смешанные стратегии 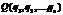 второго игрока. Чистая стратегия также подпадает под определение смешанной — если все вероятности равны нулю, кроме одной, равной единице.
второго игрока. Чистая стратегия также подпадает под определение смешанной — если все вероятности равны нулю, кроме одной, равной единице.
Пусть игроки – Первый и Второй, играют в матричную игру с матрицей 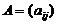 . Пусть стратегия Первого есть
. Пусть стратегия Первого есть  , а Второго –
, а Второго –  . Тогда выигрыш Первого есть случайная величина (с.в.)
. Тогда выигрыш Первого есть случайная величина (с.в.)  с рядом распределения:
с рядом распределения:

Если игроки применяют свои смешанные стратегии P (p1, p2,…pm)и Q (q1, q2,…qn) соответственно, Выигрыш первого: выигрыш aij
Вероятность pi qj.
То есть первый игрок с вероятностью pi gj. выигрывает aij.. Математическое ожидание выигрыша первого игрока равно М(P,Q)= 
 pi qj aij есть средний выигрыш.
pi qj aij есть средний выигрыш.





 =max min aij называется нижней ценой игры.
=max min aij называется нижней ценой игры.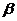 = min max a ij и соответствующая ей минимаксная стратегия второго игрока. То есть, принимая свою минимаксную стратегию второй игрок проиграет не больше
= min max a ij и соответствующая ей минимаксная стратегия второго игрока. То есть, принимая свою минимаксную стратегию второй игрок проиграет не больше  .
.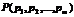 , где все
, где все 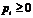 , а
, а  . При этом
. При этом 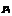 — вероятность, с которой первый игрок выбирает свою i -ю стратегию. Аналогично определяются смешанные стратегии
— вероятность, с которой первый игрок выбирает свою i -ю стратегию. Аналогично определяются смешанные стратегии 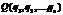 второго игрока. Чистая стратегия также подпадает под определение смешанной — если все вероятности равны нулю, кроме одной, равной единице.
второго игрока. Чистая стратегия также подпадает под определение смешанной — если все вероятности равны нулю, кроме одной, равной единице.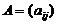 . Пусть стратегия Первого есть
. Пусть стратегия Первого есть  , а Второго –
, а Второго –  . Тогда выигрыш Первого есть случайная величина (с.в.)
. Тогда выигрыш Первого есть случайная величина (с.в.)  с рядом распределения:
с рядом распределения:

 pi qj aij есть средний выигрыш.
pi qj aij есть средний выигрыш.

