Теорема о достаточном условии оптимальности решений пары двойственных задач: Если  и
и 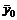 - допустимые решения пары двойственных задач, для которых выполняется равенство
- допустимые решения пары двойственных задач, для которых выполняется равенство  , то
, то  и
и 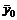 - оптимальные решения соответствующих задач.
- оптимальные решения соответствующих задач.
Согласно этой теореме, план производства продукции и вектор оценок ресурсов является оптимальным, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.
43.Сформулировать и доказать первую основную теорему двойственности. В чем состоит экономическое содержание первой основной теоремы двойственности?
Если одна из двойственных задач имеет оптимальное решение, то двойственная ей задача также имеет оптимальное решение, причем экстремумы целевых функций равны, т.е. 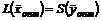 .
.
Если одна из двойственных задач не имеет оптимального решения, то другая задача также не имеет оптимального решения, причем если одна из задач не имеет оптимального решения из-за неограниченности целевой функции, то другая из-за несовместности системы ограничений.
 Д-во: Пусть существует оптимальное решение х* прямой задачи, тогда оптимальное базисное решение расширенной задачи лп существует и имеет вид:
Д-во: Пусть существует оптимальное решение х* прямой задачи, тогда оптимальное базисное решение расширенной задачи лп существует и имеет вид:
Где B* - оптимальная базисная матрица.
Оптимальное значение функции цели расширенной задачи равно
 . Но поскольку коэффициенты функции цели при дополнительных переменных расширенной задачи равны нулю, то это значение является одновременно и оптимальным значением целевой функции первоначальной задачи:
. Но поскольку коэффициенты функции цели при дополнительных переменных расширенной задачи равны нулю, то это значение является одновременно и оптимальным значением целевой функции первоначальной задачи: 
Докажем теперь, что существует оптимальное решение двойственной задачи P*/ Для этого докажем что решение двойственной задачи  допустимо, а затем то, что оно оптимально. В самом деле, поскольку решение
допустимо, а затем то, что оно оптимально. В самом деле, поскольку решение  оптимальное базисное решение расширенной задачи, то для него все симплекс-разности неположительны
оптимальное базисное решение расширенной задачи, то для него все симплекс-разности неположительны  . Но поскольку
. Но поскольку  то
то  . В первоначальной нумерации матрица неА и цены неС расширенной задачи имеют следующую структуру: неА=(А,Em) неС=(с,0). В соответствии с данной структурой неравенства
. В первоначальной нумерации матрица неА и цены неС расширенной задачи имеют следующую структуру: неА=(А,Em) неС=(с,0). В соответствии с данной структурой неравенства  разделяются на 2 части:
разделяются на 2 части: 
И  , поэтому Ро допустимое решение двойственной задачи. Кроме того, в соответствии с
, поэтому Ро допустимое решение двойственной задачи. Кроме того, в соответствии с  , поэтому согласно теореме о достаточном условии оптимельности решений пары двойственных задач лп Po является оптимельным решением. Пусть теперь целевая функция прямой задачи не ограничена. Предположим, что двойственная задача имеет допустимое решение Р тогда по основному неравенству теории двойственности значения функции цели для всех допустимых решений прямой задачи были бы ограничены сверху величиной рb, но это противоречит тому. Что ф-я цели не ограничена, поэтому двойственная задача не имеет решения.
, поэтому согласно теореме о достаточном условии оптимельности решений пары двойственных задач лп Po является оптимельным решением. Пусть теперь целевая функция прямой задачи не ограничена. Предположим, что двойственная задача имеет допустимое решение Р тогда по основному неравенству теории двойственности значения функции цели для всех допустимых решений прямой задачи были бы ограничены сверху величиной рb, но это противоречит тому. Что ф-я цели не ограничена, поэтому двойственная задача не имеет решения.
Экономическое содержание первой основной теоремы двойственности ЛП таково. В терминах оценок она может быть сформулирована следующим образом: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения минимальных оценок ресурсов, причем цена продукта, полученного реализацией оптимального плана, совпадает с суммарной оценкой имеющихся ресурсов.
44.Сформулировать и доказать вторую основную теорему двойственности. В чем состоит экономическое содержание второй основной теоремы двойственности?
Для того чтобы допустимые решения исходной  и двойственной
и двойственной 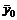 задач являлись оптимальными решениями соответствующих задач двойственной пары необходимо и достаточно выполнение следующих условий:
задач являлись оптимальными решениями соответствующих задач двойственной пары необходимо и достаточно выполнение следующих условий:
Т.е. если какое-либо нер-во системы ограничений одной из задач не обращается в точное равенство оптимальным решением этой задачи, то соответствующая компонента оптимального решения двойственной задачи должна быть равна 0. Если же какая-либо компонента оптимального решения положительна, то соотв-ее ей ограничение в двойственной задаче должно быть обращено в точное равенство.
Другими словами: 1)если хj0>0,то  aijyi0=cj; 2)если
aijyi0=cj; 2)если  aijyi0>cj, то xj0=0; 3)если yi0>0, то
aijyi0>cj, то xj0=0; 3)если yi0>0, то  aijxj0=bi; 4)если
aijxj0=bi; 4)если  aijxj0<bi,то yi0=0. j=
aijxj0<bi,то yi0=0. j=  , i=
, i= 
Если по оптимальному плану расход i-того ресурса < его запасов, то оценка этого ресурса=0. Если же оценка>0, то расход этого ресурса равен его запасу. Таким образом, дефицитный (полностью используемый по оптимальному плану) ресурс имеет положительную оценку в двойственной задаче, а недефицитный – нулевую оценку.
С точки зрения пр-ва: если оценка ресурсов, расходуемых по j-ой технологии больше цены продукта, то j-ая технология не применяется (xj=0). Если же по некот. плану j-ая технология применяется (xj>0), то оценка ресурсов, расходуемых по данной технологии, равна цене продукта.
Док-во:
Оптимальные решения Х* и Y* как допустимые решения удовлетворяют следующим неравенствам:  . Умножим первое из них на Y*, а второе на X*, тогда
. Умножим первое из них на Y*, а второе на X*, тогда  . Поскольку Y*B=CX*, то левые части неравенства равны и каждая равна нулю:
. Поскольку Y*B=CX*, то левые части неравенства равны и каждая равна нулю:
 . В развёрнутой форме
. В развёрнутой форме  ;
;  , что и требовалось доказать
, что и требовалось доказать
45. Сформулировать и доказать третью основную теорему двойственности. В чем состоит экономическое содержание третьей основной теоремы двойственности?
Пусть дана пара двойственных несимметричных задач:
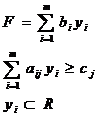

(i=1,m), (j=1,n)
Предположим, что мы решили исходную задачу:
 Zmax=Z0(X0)
Zmax=Z0(X0)

Тогда предположим, что – оптимальное решение 2ой задачи.
 Теорема: значения переменных Yi0 в оптимальном решении двойств. Задачи представляют собой оценки правых частей bi системы ограничений исходной задачи на величину максимума целевой функции:
Теорема: значения переменных Yi0 в оптимальном решении двойств. Задачи представляют собой оценки правых частей bi системы ограничений исходной задачи на величину максимума целевой функции:
Доказательство:
Экон.смысл: двойственная оценка ресурса – это приращение прибыли, приходящейся на единицу приращения этого ресурса. Здесь речь идет лишь о достаточно малых приращениях ресурсов, так как изменение величины 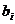 в некоторый момент вызовет изменение оценок
в некоторый момент вызовет изменение оценок  . Оценки позволяют выявить направление мероприятий по расшивке узких мест производства (ресурсы с положительной двойственной оценкой), обеспечивающих получение наибольшего экономического эффекта.
. Оценки позволяют выявить направление мероприятий по расшивке узких мест производства (ресурсы с положительной двойственной оценкой), обеспечивающих получение наибольшего экономического эффекта.
Из 2-ой и 3-ей теорем следует, что часть ресурсов, у которых двойственные оценки будут отличны от 0, необходимо будет пополнять для продолжения выпуска продукции. Недостающие ресурсы должны быть пополнены, причем в оптимальном количестве.



 и
и  - допустимые решения пары двойственных задач, для которых выполняется равенство
- допустимые решения пары двойственных задач, для которых выполняется равенство  , то
, то 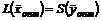 .
. Д-во: Пусть существует оптимальное решение х* прямой задачи, тогда оптимальное базисное решение расширенной задачи лп существует и имеет вид:
Д-во: Пусть существует оптимальное решение х* прямой задачи, тогда оптимальное базисное решение расширенной задачи лп существует и имеет вид: . Но поскольку коэффициенты функции цели при дополнительных переменных расширенной задачи равны нулю, то это значение является одновременно и оптимальным значением целевой функции первоначальной задачи:
. Но поскольку коэффициенты функции цели при дополнительных переменных расширенной задачи равны нулю, то это значение является одновременно и оптимальным значением целевой функции первоначальной задачи: 
 допустимо, а затем то, что оно оптимально. В самом деле, поскольку решение
допустимо, а затем то, что оно оптимально. В самом деле, поскольку решение  оптимальное базисное решение расширенной задачи, то для него все симплекс-разности неположительны
оптимальное базисное решение расширенной задачи, то для него все симплекс-разности неположительны  . Но поскольку
. Но поскольку  . В первоначальной нумерации матрица неА и цены неС расширенной задачи имеют следующую структуру: неА=(А,Em) неС=(с,0). В соответствии с данной структурой неравенства
. В первоначальной нумерации матрица неА и цены неС расширенной задачи имеют следующую структуру: неА=(А,Em) неС=(с,0). В соответствии с данной структурой неравенства 
 , поэтому Ро допустимое решение двойственной задачи. Кроме того, в соответствии с
, поэтому Ро допустимое решение двойственной задачи. Кроме того, в соответствии с  , поэтому согласно теореме о достаточном условии оптимельности решений пары двойственных задач лп Po является оптимельным решением. Пусть теперь целевая функция прямой задачи не ограничена. Предположим, что двойственная задача имеет допустимое решение Р тогда по основному неравенству теории двойственности значения функции цели для всех допустимых решений прямой задачи были бы ограничены сверху величиной рb, но это противоречит тому. Что ф-я цели не ограничена, поэтому двойственная задача не имеет решения.
, поэтому согласно теореме о достаточном условии оптимельности решений пары двойственных задач лп Po является оптимельным решением. Пусть теперь целевая функция прямой задачи не ограничена. Предположим, что двойственная задача имеет допустимое решение Р тогда по основному неравенству теории двойственности значения функции цели для всех допустимых решений прямой задачи были бы ограничены сверху величиной рb, но это противоречит тому. Что ф-я цели не ограничена, поэтому двойственная задача не имеет решения. aijyi0=cj; 2)если
aijyi0=cj; 2)если  , i=
, i= 
 . Умножим первое из них на Y*, а второе на X*, тогда
. Умножим первое из них на Y*, а второе на X*, тогда  . Поскольку Y*B=CX*, то левые части неравенства равны и каждая равна нулю:
. Поскольку Y*B=CX*, то левые части неравенства равны и каждая равна нулю: . В развёрнутой форме
. В развёрнутой форме  ;
;  , что и требовалось доказать
, что и требовалось доказать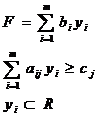

 Zmax=Z0(X0)
Zmax=Z0(X0)
 Теорема: значения переменных Yi0 в оптимальном решении двойств. Задачи представляют собой оценки правых частей bi системы ограничений исходной задачи на величину максимума целевой функции:
Теорема: значения переменных Yi0 в оптимальном решении двойств. Задачи представляют собой оценки правых частей bi системы ограничений исходной задачи на величину максимума целевой функции: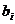 в некоторый момент вызовет изменение оценок
в некоторый момент вызовет изменение оценок  . Оценки позволяют выявить направление мероприятий по расшивке узких мест производства (ресурсы с положительной двойственной оценкой), обеспечивающих получение наибольшего экономического эффекта.
. Оценки позволяют выявить направление мероприятий по расшивке узких мест производства (ресурсы с положительной двойственной оценкой), обеспечивающих получение наибольшего экономического эффекта.

