Не имеет решения?
Имеет уравнение, являющееся линейной комбинацией каких-либо других уравнений системы?
1) Если в процессе решения появляется уравнение вида 0*х1+0*х2+…+0*хn=bi, где bi¹0, то это означает, что система несовместна, т.е. не имеет решения
2) Если в процессе решения левая и правая части i ур-я обращаются в 0, т.е.0=0 Þ данное ур-е явл линейной комбинацией ур-й входящих в эту систему, в этом случае это ур-е исключается из всей системы
По каким правилам при нахождении неотрицательных решений СЛАУ выбирается разрешающая неизвестная и разрешающее уравнение?
Решение (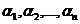 ) системы называют неотрицательным, если все его компоненты αj неотрицательны.
) системы называют неотрицательным, если все его компоненты αj неотрицательны.
Если правые части всех уравнений полученных систем окажутся неотрицательными, то соответствующие базисные решения также будут неотрицательными. Следовательно, чтобы получить неотрицательные базисные решения СЛАУ, надо научиться вести процесс исключения неизвестных так, чтобы свободные члены всех уравнений на всех этапах этого процесса оставались неотрицательными. Для этого следует руководствоваться следующими правилами: 1)Если в СЛАУ имеются отрицательные свободные члены, то все такие уравнения необходимо умножить на (-1); 2) В качестве разрешающей неизвестной можно принять любую неизвестную, при которой есть хоть один положительный коэффициент, а затем в качестве разрешающего уравнения следует взять то уравнение, которое соответствует наименьшему среди отношений свободных членов уравнений к соответствующим положительным коэффициентам при выбранной неизвестной в этих уравнениях.
Может случиться, что указанное минимальное отношение достигается при нескольких значениях индекса. Тогда любое из соответствующих им уравнений можно принять за разрешающее. Принято говорить в этом случае, что рассматриваемая СЛАУ является вырожденной.
СЛАУ не будет иметь ни одного неотрицательного решения, если в процессе симплексных преобразований в ней появится уравнение, в котором свободный член строго положителен, а среди коэффициентов при неизвестных нет ни одного положительного.
Преобразования системы в соответствии с этими правилами называются симплекс-преобразованиями системы.
7. Дайте определения:
Разрешающей неизвестной,
Разрешающего уравнения,
Базисной и свободной переменной,
Базисного и общего решения.
Разрешающая неизвестная- неизвестная в СЛАУ с коэффициентом отличным от нуля,которую собираемся исключить из всех уравнений системы, кроме r-го уравнения(разрешающего).
Разрешающее уравнение – уравнение, содержащее разрешающую неизвестную, а остальные уравнения этой системы ее не содержат.
Переменные, коэффициенты при которых образуют минор, отличный от нуля (базисный минор), называются базисными переменными (x1, x2, …, xr), переменные присутствующие только в одном уравнении системы с коэффициентом 1. Остальные переменные xr+1, …, xn называются свободными.
Общее решение- выражения базисных неизвестных через свободные вида
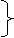 X1=h1-g1,m+1 - …- g1nxn,
X1=h1-g1,m+1 - …- g1nxn,
Xm = gm,m+1xm+1 - … - gmnxn
Среди частных решений системы выделяются базисное, отвечающее нулевым значениям свободных неизвестных: X1 = h1, x2 = h2, …, xm = hm, xm+1 = 0, …,Xn = 0
8. Матрица A = 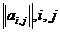 = 1,2,3. Разложите определитель
= 1,2,3. Разложите определитель 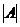 по элементам второго столбца.
по элементам второго столбца.
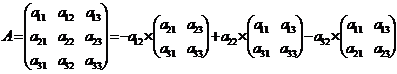
9. Дайте определения ранга матрицы размером т*n. Определите ранг матрицы (матрица задана)

Полезно иметь ввиду, что ранг матрицы не изменяется от элементарных преобразований. Под элементарными преобразованиями понимаются:
1) замена строк столбцами, а столбцов соответствующими строками;
2) перестановка строк матрицы;
3) вычеркивание строки, все элементы которой равны нулю;
4) умножение какой-либо строки на число, отличное от нуля;
5) прибавление к элементам одной строки соответствующих элементов другой строки.
Пример на определение ранга матрицы:
Нахождение ранга матрицы с помощью вычисления всех ее миноров требует слишком большой вычислительной работы. Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений.
Элементарные преобразования матриц:
1) перестановка строк или столбцов;
2) умножение строки или столбца на число отличное от нуля;
Постановка общей задачи математического программирования. Основные понятия
Задачу линейного программирования нередко формулируют как задачу минимизации или максимизации линейной формы L=c1x1+c2x2+...cnxn (1) при ограничениях x1≥0, x2≥0,...xn≥0 и
∑ aijxj≤bi, i=1,2,...m1,
∑ aijxj=bi, i= m1+1, m1+2,...m2,
∑ aijxj≥bi, i= m2+1, m2+2,...m.
Такую запись называют общей задачей линейного программирования.
Обозначим через А матрицу системы линейных уравнений:
а11x1 + a12x2 + … a1nxn = b1
а21x1 + a22x2 + … a2nxn = b2 (2)
А =.....
аm1x1 + am2x2 + … amnxn = bm.
Через X и B – матрицы-столбцы (векторы) неизвестных и свободных членов:
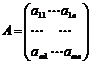 ,
, 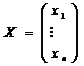 ,
, 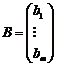
а также введем в рассмотрение n-мерный вектор C = (с1 … сn), компонентами которого служат коэффициенты линейной формы (1), и n-мерный нуль-вектор 0 (0, 0, …, 0). Тогда линейную форму можно рассматривать как скалярное произведение L=CX (3), систему линейных уравнений (2) заменить одним матричным уравнением AX=B (4), а условия x1≥0, x2≥0,...xn≥0 записать в виде X≥ 0 (5). Поэтому часто основную задачу линейного программирования кратко записывают как задачу минимизации(максимизации) линейной формы (3) при линейных ограничениях (4) и (5).
Основные понятия в теории графов: Дуги, вершины в ориентированном и неориентированном графе. Примеры применения теории графов в экономике.
Граф-это совокупность двух множеств: множества Х, элементы которого называют вершинами, и множества У упорядоченных пар вершин, элементы которого называют дугами или ребрами. Если отрезки, соединяющие вершины графа, имеют направления, то граф называется ориентированным, а сами отрезки — дугами. Если же отрезки не имеют направления, то граф называется неориентированным, и в этом случае говорят, что вершины графа соединены ребрами.
Применение в экономике: задача выбора кратчайшего пути от пункта производства до пункта конечного потребления, задача выбора схемы подключения домов к системе кабельного телевидения, при которой общая длина всех участков минимальна, задача определения максимального объема информации, который можно передать от определенного отправителя к конкретному получателю, с учетом пропускных способностей каналов и узлов системы передачи данных.
20. Экономический смысл двойственной задачи к модели оптимального планирования производства. Математическая модель задачи определения расчетных оценок ресурсов
Теория двойственности является центральной частью всего ЛП. Она имеет богатое экономическое содержание.
В рамках модели ЛП предприятия должна существовать внутренняя система оценки ресурсов, используемых им в процессе производства. Эти оценки связаны с технологическими особенностями данного производственного процесса, характеризуемыми матрицей условий A, со структурой и количеством ресурсов, отпущенных для производственного потребления, описываемых вектором B, а также со структурой внешних цен, на основе которых получается вектор прибылей C. Эти оценки называют расчетными оценками ресурсов. Расчетную оценку единицы ресурса не следует отождествлять с той ценой, по которой предприятию был отпущен этот ресурс. Последняя отражает общественно необходимые затраты на производство единицы ресурса, а расчетная цена показывает только сравнительную ценность этого ресурса на данном предприятии в данных конкретных условиях.
В зависимости от вида исходной задачи линейного программирования различают симметричные и несимметричные пары двойственных задач.
Если система ограничений исходной задачи состоит из неравенств и на все переменные хj наложено условие неотрицательности, то исходная задача и составленная по определенному правилу двойственная задача образуют симметричную пару двойственных задач.
Пусть исходная задача имеет вид: найти наибольшее значение функции
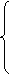
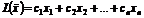
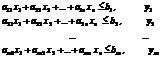
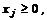
Правило составления двойственных задач
1. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная y i, где 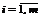 .
.
2. Составляется целевая функция 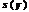 , коэффициентами которой будут свободные члены системы ограничений исходной задачи, а цель задачи меняется на противоположную:
, коэффициентами которой будут свободные члены системы ограничений исходной задачи, а цель задачи меняется на противоположную:
 (1)
(1)
3. Составляется система ограничений двойственной задачи, при этом матрица из коэффициентов системы ограничений исходной задачи транспонируется, знак неравенства меняется на противоположный, свободными членами будут являться коэффициенты из целевой функции исходной задачи:
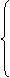
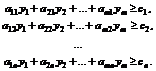 (2)
(2)
4. Переменные y i в двойственной задаче также неотрицательны, т.е.
 . (3)
. (3)
Если двойственную задачу принять за исходную и по данному правилу составить двойственную задачу, то получим исходную задачу. Понятие двойственности является взаимным.
В несимметричном случае двойственная задача составляется по тем же правилам, что и в случае симметричной пары, но если двойственная переменная поставлена в соответствие ограничению уравнения, то эта переменная свободна по знаку.
Постановка и математическая модель транспортной задачи, в которой суммарные запасы продукции меньше суммарных запросов на нее. Записать правила сведения такой модель к замкнутой задаче и записать полученную замкнутую модель транспортной задачи.
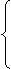 Если
Если 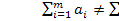 , то транспортная задача является незамкнутой. Пусть
, то транспортная задача является незамкнутой. Пусть 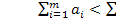 , т.е. суммарные запасы продукции меньше суммарных потребностей в ней и математическая модель открытой ТЗ имеет вид: найти наименьшее значение функции L=
, т.е. суммарные запасы продукции меньше суммарных потребностей в ней и математическая модель открытой ТЗ имеет вид: найти наименьшее значение функции L= 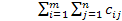 min при ограничениях:
min при ограничениях: 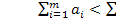 ,
,
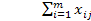 , j=1,…,n,
, j=1,…,n,
 =
=  , i=1,…,m
, i=1,…,m
 , i=1,…,m; j=1,…,n.
, i=1,…,m; j=1,…,n.
Если безразлично, какой из потребителей недополучит продукцию, то ТЗ сводится к закрытой замкнутой модели путём введения дополнительного фиктивного (m+1)-ого поставщика с запасом продукции, равным 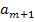 =
= 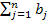 -
- 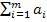 . При этом значения тарифов
. При этом значения тарифов 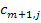 полагаем равными нулю, что обеспечивает равенство целевых функций исходных и соответствующих им вспомогательных задач. В итоге получаем замкнутую модель ТЗ. Математическая модель ТЗ: найти план перевозок X=(
полагаем равными нулю, что обеспечивает равенство целевых функций исходных и соответствующих им вспомогательных задач. В итоге получаем замкнутую модель ТЗ. Математическая модель ТЗ: найти план перевозок X=( 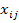 ), i=1,2,…,m; j=1,2,…,n, минимизирующий общую стоимость всех перевозок L=
), i=1,2,…,m; j=1,2,…,n, минимизирующий общую стоимость всех перевозок L= 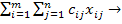 min при условии, что из любого пункта производства вывозится весь продукт:
min при условии, что из любого пункта производства вывозится весь продукт: 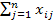 =
= 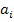 , i=1,2,…,m и любому потребителю доставляется необходимое количество груза:
, i=1,2,…,m и любому потребителю доставляется необходимое количество груза: 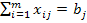 , j=1,2,…,n, причём по смыслу задачи
, j=1,2,…,n, причём по смыслу задачи 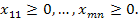 Решаем её, находим оптимальный план. При этом значения
Решаем её, находим оптимальный план. При этом значения 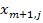 в решении вспомогательной задачи будут обозначать величину неудовлетворённого спроса j-ого потребителя.
в решении вспомогательной задачи будут обозначать величину неудовлетворённого спроса j-ого потребителя.
Постановка и математическая модель транспортной задачи, в которой суммарные запасы продукции больше суммарных запросов на нее. Записать правила сведения такой задачи к замкнутой и записать полученную замкнутую модель транспортной задачи.
Пусть 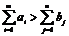 , т е суммарные запасы продукции больше суммарных потребностей в ней. Если безразлично, у кого из поставщиков останутся излишки продукции, то решение такой несбалансированной задачи сводится к решению замкнутой транспортной задачи путем введения дополнительного фиктивного (n-1)го потребителя, запросы которого составляют
, т е суммарные запасы продукции больше суммарных потребностей в ней. Если безразлично, у кого из поставщиков останутся излишки продукции, то решение такой несбалансированной задачи сводится к решению замкнутой транспортной задачи путем введения дополнительного фиктивного (n-1)го потребителя, запросы которого составляют
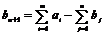
Значение сi, n+1 полагаем равным нулю и решаем вспомогательную задачу с n+1 потребителем и m поставщиками. При этом продукция xi,n+1 , планируемая для перевозки к фиктивному потребителю, остается на i-м складе.
Записать математическую модель замкнутой транспортной задачи, составить двойственную к ней задачу и записать условия второй основной теоремы двойственности для получения пары взаимодвойственных задач линейного программирования.
Транспортная задача,в которой суммарные запасы продукции поставщиков = суммарным запросам потребителей, называется сбалансированной, закрытой или замкнутой.В этом случае удовлетворение запросов всех потребителей возможно, если от каждого поставщика вывозится вся продукция, а каждому потребителю продукция доставляется в количестве, соответствующем его запросам. Очевидно,что математической моделью закрытой транспортной задачи будет следующая задача ЛП:
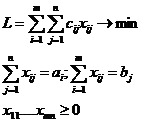 (1.3);(1,4)
(1.3);(1,4)
Отметим 2 важных свойства задачи ():
1)задача всегда имеет решение
2)ранг матрицы коэффициентов системы уравнений равен m+n-1.
Дохода?
Не имеет решения?
имеет уравнение, являющееся линейной комбинацией каких-либо других уравнений системы?
1) Если в процессе решения появляется уравнение вида 0*х1+0*х2+…+0*хn=bi, где bi¹0, то это означает, что система несовместна, т.е. не имеет решения
2) Если в процессе решения левая и правая части i ур-я обращаются в 0, т.е.0=0 Þ данное ур-е явл линейной комбинацией ур-й входящих в эту систему, в этом случае это ур-е исключается из всей системы





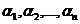 ) системы называют неотрицательным, если все его компоненты αj неотрицательны.
) системы называют неотрицательным, если все его компоненты αj неотрицательны.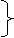 X1=h1-g1,m+1 - …- g1nxn,
X1=h1-g1,m+1 - …- g1nxn,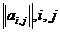 = 1,2,3. Разложите определитель
= 1,2,3. Разложите определитель 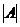 по элементам второго столбца.
по элементам второго столбца.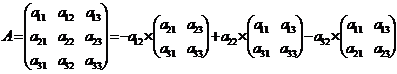

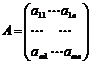 ,
, 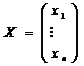 ,
, 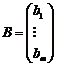
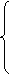
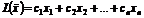
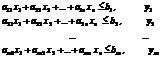
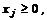
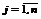
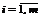 .
.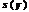 , коэффициентами которой будут свободные члены системы ограничений исходной задачи, а цель задачи меняется на противоположную:
, коэффициентами которой будут свободные члены системы ограничений исходной задачи, а цель задачи меняется на противоположную: (1)
(1)
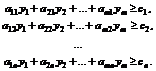 (2)
(2) . (3)
. (3) Если
Если 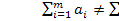 , то транспортная задача является незамкнутой. Пусть
, то транспортная задача является незамкнутой. Пусть 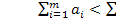 , т.е. суммарные запасы продукции меньше суммарных потребностей в ней и математическая модель открытой ТЗ имеет вид: найти наименьшее значение функции L=
, т.е. суммарные запасы продукции меньше суммарных потребностей в ней и математическая модель открытой ТЗ имеет вид: найти наименьшее значение функции L= 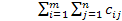 min при ограничениях:
min при ограничениях: 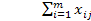 , j=1,…,n,
, j=1,…,n, =
=  , i=1,…,m
, i=1,…,m , i=1,…,m; j=1,…,n.
, i=1,…,m; j=1,…,n.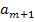 =
= 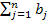 -
- 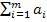 . При этом значения тарифов
. При этом значения тарифов 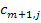 полагаем равными нулю, что обеспечивает равенство целевых функций исходных и соответствующих им вспомогательных задач. В итоге получаем замкнутую модель ТЗ. Математическая модель ТЗ: найти план перевозок X=(
полагаем равными нулю, что обеспечивает равенство целевых функций исходных и соответствующих им вспомогательных задач. В итоге получаем замкнутую модель ТЗ. Математическая модель ТЗ: найти план перевозок X=( 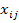 ), i=1,2,…,m; j=1,2,…,n, минимизирующий общую стоимость всех перевозок L=
), i=1,2,…,m; j=1,2,…,n, минимизирующий общую стоимость всех перевозок L= 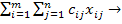 min при условии, что из любого пункта производства вывозится весь продукт:
min при условии, что из любого пункта производства вывозится весь продукт: 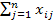 =
= 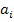 , i=1,2,…,m и любому потребителю доставляется необходимое количество груза:
, i=1,2,…,m и любому потребителю доставляется необходимое количество груза: 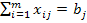 , j=1,2,…,n, причём по смыслу задачи
, j=1,2,…,n, причём по смыслу задачи 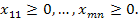 Решаем её, находим оптимальный план. При этом значения
Решаем её, находим оптимальный план. При этом значения 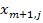 в решении вспомогательной задачи будут обозначать величину неудовлетворённого спроса j-ого потребителя.
в решении вспомогательной задачи будут обозначать величину неудовлетворённого спроса j-ого потребителя.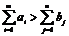 , т е суммарные запасы продукции больше суммарных потребностей в ней. Если безразлично, у кого из поставщиков останутся излишки продукции, то решение такой несбалансированной задачи сводится к решению замкнутой транспортной задачи путем введения дополнительного фиктивного (n-1)го потребителя, запросы которого составляют
, т е суммарные запасы продукции больше суммарных потребностей в ней. Если безразлично, у кого из поставщиков останутся излишки продукции, то решение такой несбалансированной задачи сводится к решению замкнутой транспортной задачи путем введения дополнительного фиктивного (n-1)го потребителя, запросы которого составляют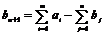
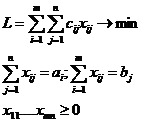 (1.3);(1,4)
(1.3);(1,4)

