Применяя метод сечений, легко убедиться, что крутящий момент во всех поперечных сечениях бруса одинаков: 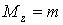 . Выразим его через касательные напряжения, возникающие в поперечном сечении. При этом учтем, что в любой точке поперечного сечения касательное напряжение направлено перпендикулярно к радиусу, проведенному в эту точку (рис.7.8).
. Выразим его через касательные напряжения, возникающие в поперечном сечении. При этом учтем, что в любой точке поперечного сечения касательное напряжение направлено перпендикулярно к радиусу, проведенному в эту точку (рис.7.8).
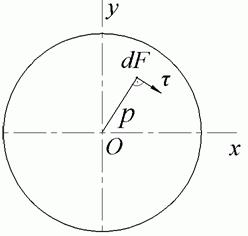
Рис.7.8. Касательное напряжение
Такое направление напряжений следует из характера деформации: при повороте произвольного поперечного сечения (рис.7.7) каждая его точка (кроме лежащей на оси бруса) перемещается по дуге окружности, концентричной контуру сечения. Иными словами, направление этого перемещения, а значит и возникающего в этой точке касательного напряжения, перпендикулярно соответствующему радиусу (рис.7.9).

Рис.7.9. Направление перемещения и касательного напряжения
Элементарная касательная сила, приходящаяся на площадку  , равна
, равна  , а ее момент относительно оси
, а ее момент относительно оси  (точки О):
(точки О):

Суммируя эти элементарные моменты, получаем следующее выражение для крутящего момента:
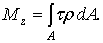
| (7.4)
|
Хотя крутящий момент может рассматриваться как известная величина (определяется с помощью метода сечений через заданные внешние моменты), использовать выражение (7.4) для вычисления касательных напряжений невозможно, так как закон их распределения по поперечному сечению пока неизвестен. Для выяснения этого закона рассмотрим более подробно вопрос о деформациях.
Выделим часть бруса двумя бесконечно близкими поперечными сечениями (рис.7.7). Будем считать выделенную часть бруса защемленной в сечении I (рис.7.9), что вполне допустимо, так как нас интересуют ее деформации, а не перемещения в пространстве как твердого тела. Точка В, взятая на контуре сечения II, в результате его поворота на угол  перейдет в положение
перейдет в положение 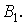 Деформация сдвига соответствующего элемента бруса (торец этого элемента, лежащий в сечении II, зачернен) характеризуется углом сдвига
Деформация сдвига соответствующего элемента бруса (торец этого элемента, лежащий в сечении II, зачернен) характеризуется углом сдвига 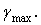 Из прямоугольного треугольника
Из прямоугольного треугольника  , учитывая, что
, учитывая, что  , и в силу малости деформаций
, и в силу малости деформаций 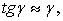 получаем
получаем
 Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса
Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса 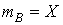 (рис.7.9), и повторяя те же рассуждения, имеем
(рис.7.9), и повторяя те же рассуждения, имеем
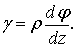
| (7.5)
|
Применяя закон Гука для сдвига (  ), получаем следующее выражение для касательного напряжения
), получаем следующее выражение для касательного напряжения

| (7.6)
|
Подставляя (7.6) в (7.4), получаем 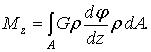
При интегрировании по площади поперечного сечения величина  постоянна и, так же как и G, может быть вынесена за знак интеграла:
постоянна и, так же как и G, может быть вынесена за знак интеграла:
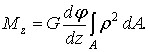
| (7.7)
|
Интеграл, входящий в выражение (7.7), представляет собой полярный момент инерции сечения  (см. раздел 2), следовательно,
(см. раздел 2), следовательно,

откуда
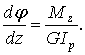
| (7.8)
|
Подставим (7.8) в (7.6):
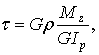
или окончательно
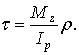
| (7.9)
|
Формула (7.9) позволяет определить величину касательного напряжения в любой точке поперечного сечения. Из этой формулы следует, что касательные напряжения распределены вдоль любого радиуса сечения по линейному закону.
Эпюры касательных напряжений для круглого сплошного и кольцевого поперечных сечений показаны на рис.7.10.
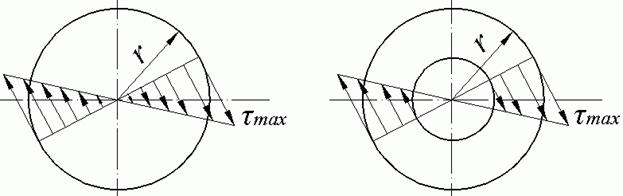
Рис.7.10
В точках, равноудаленных от центра сечения, напряжения одинаковы. Наибольшего значения касательные напряжения достигают в точках контура поперечного сечения. Они могут быть определены путем подстановки в (7.9) вместо 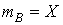 его наибольшего значения, т. е.
его наибольшего значения, т. е.  :
:

Величина 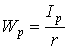 представляет собой полярный момент сопротивления (см. раздел 2), следовательно, получим следующее выражение для максимального касательного напряжения:
представляет собой полярный момент сопротивления (см. раздел 2), следовательно, получим следующее выражение для максимального касательного напряжения:





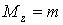 . Выразим его через касательные напряжения, возникающие в поперечном сечении. При этом учтем, что в любой точке поперечного сечения касательное напряжение направлено перпендикулярно к радиусу, проведенному в эту точку (рис.7.8).
. Выразим его через касательные напряжения, возникающие в поперечном сечении. При этом учтем, что в любой точке поперечного сечения касательное напряжение направлено перпендикулярно к радиусу, проведенному в эту точку (рис.7.8).

 , равна
, равна  , а ее момент относительно оси
, а ее момент относительно оси  (точки О):
(точки О):
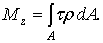
 перейдет в положение
перейдет в положение 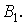 Деформация сдвига соответствующего элемента бруса (торец этого элемента, лежащий в сечении II, зачернен) характеризуется углом сдвига
Деформация сдвига соответствующего элемента бруса (торец этого элемента, лежащий в сечении II, зачернен) характеризуется углом сдвига 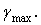 Из прямоугольного треугольника
Из прямоугольного треугольника  , учитывая, что
, учитывая, что  , и в силу малости деформаций
, и в силу малости деформаций 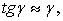 получаем
получаем Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса
Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса 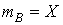 (рис.7.9), и повторяя те же рассуждения, имеем
(рис.7.9), и повторяя те же рассуждения, имеем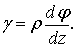
 ), получаем следующее выражение для касательного напряжения
), получаем следующее выражение для касательного напряжения
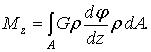
 постоянна и, так же как и G, может быть вынесена за знак интеграла:
постоянна и, так же как и G, может быть вынесена за знак интеграла: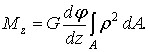
 (см. раздел 2), следовательно,
(см. раздел 2), следовательно,
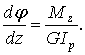
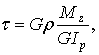
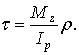

 :
:
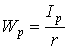 представляет собой полярный момент сопротивления (см. раздел 2), следовательно, получим следующее выражение для максимального касательного напряжения:
представляет собой полярный момент сопротивления (см. раздел 2), следовательно, получим следующее выражение для максимального касательного напряжения:


