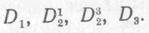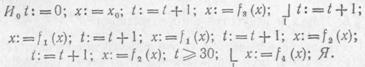Мы видим, что идея алгоритмизации процессов для человечества не нова. Она уже ставилась в отдельных областях человеческой деятельности и решалась. Но при этом она не была осознана как проблема алгоритмизации. Этот важный шаг был совершен человечеством лишь после появления ЭВМ и довольно значительного развития идей программирования. Естественно, что и идея универсального языка, удобного для алгоритмизации пр< це.сов, возникла в тесной связи с развитием языков программирования.
В 1953 г. известный советский математик А. А. Ляпунов сформировал понятие оператора в теории программирования, пользуясь которым от алгоритма, описывающего некоторый процесс, удобно переходить к программе ЭВМ. Первоначально операторный метод применялся как некоторый этап программирования. В несколько видоизмененном виде он и сейчас применяется для тех же целей. Дальнейшее развитие операторного метода оказало глубокое влияние на развитие как методов программирования, так и методов алгоритмизации.
Операторами называются описания функционально однородных этапов изучаемого процесса. Операторы делятся на действующие, логические и варьирующие. Действующие операторы определяют изменения, происходящие в объектах. Именно они передают существо описываемого процесса. Логические операторы представляют собой описание условий, от которых зависит направление процесса. Наконец, варьирующие операторы — это операторы, предусматривающие изменения вспомогательных величин, называемых параметрами. Обычно параметры являются либо номерами изменяемых объектов, имеющих одинаковые имена, либо номерами операторов, почему-либо объединенных в одну группу; так что изменение параметров означает либо переход от одних объектов к другим, либо выбор некоторого оператора из группы операторов. Кроме указанных трех типов операторов, существуют еще операторы перехода, указывающие порядок выполнения операторов первых трех типов; их называют знаками перехода. Действующие операторы обозначаются символами D1 D10, D20 и т. д. Если действующий оператор зависит от параметров, например i, j, то он обозначается знаками 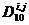 ,
, 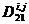 и т. п.
и т. п.
Варьирующие операторы обычно сами не зависят от параметров, но изменяют значения параметров; их обозначают символами V5(i), V10 (i, j), указывая в скобках наименования параметров, которые они изменяют (варьируют).
Логические операторы обозначают буквой Р, снабженной снизу номером, а сверху индексами, обозначающими параметры (если эти операторы зависят от параметров), так что для обозначения логических операторов применяют знаки Р5, 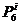 ,
, 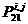 и т. п.
и т. п.
Знаки перехода обозначают в виде полускобок, снабженных числовым индексом:
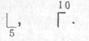
Кроме перечисленных, применяют знак, указывающий начало процесса (И0), конец процесса (Я, Я7, Я10 и т. д.) и так называемый знак приема управления, имеющий вид правой нижней полускобки, снабженной числовым индексом. Он может соответствовать как верхнему, так и нижнему знаку перехода. Соответствие определяется равенством числовых индексов. Выглядит знак приема управления так:
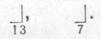
После логического оператора должны стоять два знака перехода — один верхний (случай «да»), другой — нижний (случай «нет»), после нелогического — один знак перехода: нижний.
Описанием процесса является строка операторов и знаков перехода. При этом знаки перехода от какого-либо оператора к оператору, непосредственно за ним следующему, подразумеваются, но не пишутся. После каждого нелогического оператора, включая и знак начала, может быть только один знак перехода (явный или воображаемый). После знака конца процесса знаков перехода быть не может. Знак начала и знак конца процесса тоже называют операторами.
Если между двумя операторами стоит знак приема управления, то его присутствие не отделяет операторы друг от друга. Строка
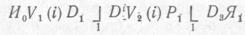
может служить описанием некоторого процесса. Оно может
быть таким:
1. Оператор V1 (i) задает начальное значение параметра, например i=l.
2. Выполняется оператор D1.
3. Выполняется оператор 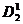 .
.
4. Оператор V2(i) изменяет значение параметра. Например, делает его равным i=3.
5. Оператор P1 проверяет некоторое условие. Допустим, ответ получился отрицательный. Тогда управление передается знаком перехода оператору, стоящему после знака приема управления
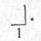
6. Выполняется оператор 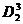 .
.
7. Оператор V2 (i) снова меняет значение параметра. Например, делает его i = 10.
8. Оператор P1 проверяет соответствующее условие. Допустим, что теперь получен ответ «да». Должен выполняться верхний знак перехода. Его нет. Значит, он воображаемый.
9. Выполняется оператор D3.
10. Процесс окончен, так как далее следует оператор Я1
Итак, в соответствии с нашим истолкованием строки операторов, был выполнен процесс
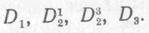
Само собой разумеется, что смысл операторов должен быть задан.
Первым этапом процесса алгоритмизации является построение строки операторов, описание которых осуществлено неформально. Например, оно может быть сделано на естественном, но достаточно точном языке.
Полученная при этом схема процесса называется его логической схемой. Блок-схема является частным случаем логической схемы, конечно, если она построена с соблюдением правил определения операторов.
Следующим этапом описания процесса является формальное описание каждого оператора. При этом логическая схема превратится в запись алгоритма на языке логических схем.
Язык логических схем фактически является целым семейством языков, так как применяемые в нем символы объектов и операций не имеют раз и навсегда заданного смысла. Придавая им конкретный смысл, мы получим одну из конкретных реализаций языка логических схем.
В основе способа точного описания операторов лежит следующая идея. Процесс рассматривают как некоторуь последовательность изменений состояний некоторой системы объектов. Объекты обозначаются буквами (или буквами с индексами), играющими роль их имен. Если это существенно, одним из объектов считается время. Считается, что каждый объект остается в одном и том же состояние до тех пор, пока его не изменит один из действующих операторов. Операторы могут не только изменять состояния объектов и значения параметров, но и создавать новые объекты и параметры.
В начале процесса ряд объектов находится в некоторой начальном состоянии. Каждый действующий оператор пред ставляет собой последовательность формул вида
y:= f(x, y, z,...).
Такая формула означает, что результат выполнения операции f над значениями (состояниями) объектов х, у, z,... нужно считать новым значением (состоянием) объекта у, указанного в левой части формулы.
Если в формулах указаны буквы, снабженные буквенными индексами, то перед выполнением операции всем индексам нужно придать значения соответствующих этим индексам параметров.
Аналогично записываются варьирующие операторы, с той разницей, что в них фигурируют математические операции, поскольку значениями параметров являются целые неотрицательные числа.
Логические операторы записываются в виде отдельных выражений р(х,у,z,...), обозначающих различные условия.
После того как операторы указанным способом описаны, делают одно из двух. Либо в логической схеме каждый оператор заменяют его описанием, либо в конце логической схемы в квадратных скобках выписывают так называемые расшифровки всех операторов. Каждая расшифровка состоит из знака, обозначающего оператор, и написанных вслед за этим знаком формул, представляющих его смысл[28].
В рамках данной книги автор не может дать более точного описания языка логических схем. Все же следует попытаться привести какой-либо очень простой, но достаточно ясный пример его применения. Предположим, что необходимо описать движения человека, совершающего простейшие гимнастические упражнения, известные под названием физической зарядки.
В данном случае объектами, состояниями которых определяется процесс, являются внутреннее время (время, отсчет которого начинается с момента начала процесса) и человек, совершающий физическую зарядку. Состояниями человека будем считать различные его позы, а под операциями будем понимать движения, приводящие к изменениям поз. Пусть f1 означает движение обеими руками впереди корпуса снизу вверх, при котором угол, образуемый руками и корпусом, изменяется на 90°; операция f 2 означает движение обеими руками вниз и в разные стороны так, что обе руки и корпус остаются в одной плоскости, а угол между каждой рукой и корпусом изменяется на 90°. Каждая операция считается применимой лишь к такой позе, находясь в которой человек способен совершить соответствующее движение (например, если человек стоит, разведя руки в стороны на уровне плеч, то операция f1 неприменима). Символом f 3 обозначим операцию, заключающуюся в сжатии (из естественного положения) кистей обеих рук в кулаки, а символом f 4 — обратную ей операцию, в результате которой кисти принимают естественное положение с полусогнутыми пальцами.
Обозначим время буквой t, человека в произвольной позе — буквой х, а того же человека, стоящего в стойке «смирно»,— буквой х0. Нетрудно прочесть следующую запись и представить себе изображенный ею процесс:
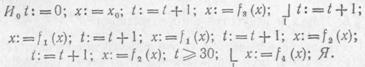
Описываемый процесс состоит в том, что человек х в момент t = 0 принимает позу х0 (стойку «смирно»), в момент t = 1 он сжимает руки в кулаки. После этого в момент t = 2 он поднимает их перед собой до уровня плеч, готом в момент t=3 еще раз поднимаем их перед собой (теперь обе руки протянуты вверх); далее, в момент t = 4 руки разводятся в обе стороны до уровня плеч; далее, в момент t — 5 они опускаются вниз. Затем, если t<30, процесс повторяется, начиная с подъема рук снизу вверх впереди себя на 90°. Если в момент выполнения логического оператора окажется, что время больше или равно 30, то кисти рук расслабляются, и процесс считается оконченным. Если нужна большая точность, то операции могут быть заданы с помощью рисунков или серий рисунков.
Читатель, конечно, понял, что подобным образом можно описать и более сложные процессы. Например, можно описать известный танец маленьких лебедей из балета «Лебединое озеро». Это значит, что, построив достаточно совершенные роботы, мы могли бы их заставить исполнять даже балетные номера. Качество исполнения будет зависеть от точности задания операций и, конечно, от качества и внешнего вида роботов.
Программную модель процесса мы получим, заменяя объекты процесса их математическими образами, а операции, фигурирующие в описании процесса, выполненном на языке логических схем, соответствующими математическими операциями. Нужно только, чтобы каждому еозмож-ному состоянию объекта соответствовало определенное состояние (или значение) его математической модели.
В описанном процессе физзарядки человек находится всегда в одном из пяти состояний, для получения которых задано 4 операции (не считая тождественной операции, использованной в операторе х:= лг0). Следовательно, человека, выполняющего описанное гимнастическое упражнение, можно было бы представить в виде переменной, которая в начальный момент имеет состояние, изображаемое числом 0, а затем в течение некоторого времени пробегает значения 1,2,3,4,5, 2,3,4,5, 2,3,4,5, 2,3,4,5, 2,3,4,5, 2,3,4,5, 2,3,4,5, 2,3,4,5, 1.





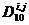 ,
, 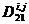 и т. п.
и т. п.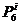 ,
, 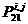 и т. п.
и т. п.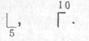
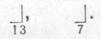
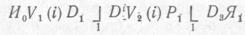
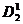 .
.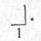
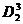 .
.