Исследование тупиков (клинчей)

Исследуя поведение коллективов алгоритмов, нужно выяснить, что произойдет, если какой-либо критический шаг некоторого а-фрагмента окажется невыполнимым? От­вет на этот вопрос несложен. В такой ситуации безрезуль­татно становится не только тот частный процесс, которому принадлежит невыполнимый критический шаг, но и все частные процессы, содержащие критические шаги а-фраг­мента, со специальными номерами, большими, чем у невыполнимого критического шага. Совокупный процесс при этом безрезультатно оборвется, хотя некоторые из частных процессов могут и завершиться. Описанное явление харак­теризуют словами «совокупный процесс зашел в тупик» или «некоторые частные процессы вошли в клинч» («клинч» — это широко известное словечко из боксерского жаргона). Будем коротко говорить (хотя это и неточно): произошел тупик (клинч).

Каковы же могут быть причины тупика? Существуют три такие причины: 1) в критическом фрагменте может отсутст­вовать зафиксированный в нем критический шаг (несколь­ко критических шагов); 2) существуют два критические ша­га такие, что первый предшествует второму, а второй пред­шествует первому; 3) при выполнении совокупного процес­са возникают запреты таких критических шагов, за кото­рыми следуют критические шаги, снимающие запреты из числа указанных. Рассмотрим подробнее каждую из ука­занных причин.

1) Коллектив алгоритмов, при совокупном выполнении которого имеются пропуски критических шагов, называет­ся открытым в отличие от остальных коллективов, назы­ваемых закрытыми. При выполнении открытого коллекти­ва возможно внешнее вмешательство в его функциониро­вание (чтение несобственного элемента или и чтение, и запись). Поэтому тупики, связанные с пропуском критиче­ского шага, называются устранимыми извне. Открытые кол­лективы алгоритмов можно применять при создании слож­ных автоматов и роботов.

Примером открытого коллектива может служить сле­дующая пара алгоритмов, исходными данными для кото­рой являются таблицы типа табл. 9 (в которых а=1). Алгоритм 1. 1) Сделать а— 2. Перейти к п. 2.

2) Увеличить x на 1. Перейти к п. 3.

3) Если а=1, то перейти к п. 4, иначе перейти к п. 3.

4) Увеличить у на 1. Перейти к п. 5.

5) Сделать а=0. Конец.

Алгоритм 2. 1) Возвести значение г в квадрат. Пе­рейти к п. 2.

2) Если а=0, то перейти к п. 3, иначе перейти к п. 2.

3) Считать, что у*z является новым значением г. Перейти к п. 4.

4) Сделать а равным 1. Конец.

Если этот коллектив алгоритмов применить к табл. 9, то оба алгоритма остановятся, причем операнд примет вид, изображенный на табл. 13. Равенство величины а числу 2

является признаком возможности внешнего вмешательства. Допустимо изменение значений как у, так и а. Как только мы придадим а значение 0 или значение 1, коллектив снова начнет работать и больше ничего в операнде менять нельзя. Предположим, что величину у мы менять не стали. Тогда, если сделать а=0, то выполнение коллектива приведет к результату, показанному на табл. 14, если же сделать а= 1,

то будет получен результат, приведенный на табл. 15. Вполне естественно, что от характера вмешательства зави­сит получаемый результат.

2) Существование двух критических шагов таких, что каждый из них является предшествующим для другого, ча­ще всего связано с наличием ошибки. Впрочем, возможно, что при одном исходном данном тупик, связанный с «конф­ликтом порядков», возникает, а при другом — не возникает. Во всяком случае, если для какого-нибудь исходного данного он возник, то при всяком повторном применении коллектива к этому исходному данно­му он будет всегда возникать, и сово­купный процесс будет всегда безре­зультатно обрываться. Поэтому тупи­ки этого рода называют абсолютными. Поясним возникновение абсолют­ного тупика на простом примере. Предположим, что коллектив двух ал­горитмов выполняется для некоторого операнда и что в операнде имеется два несобственных элемента аир. Предпо­ложим, что выполнение алгоритмов протекает так, как это показано на схеме, приведенной на рис. 18. На этой схеме каждый част­ный процесс изображен в виде ориентированного отрезка, на котором выделены точки, являющиеся изображениями шагов. Пометками 1_αи 2 _αуказан специальный порядок двух шагов, принадлежащих α-фрагменту, а пометками 1 _βи 2 _β — специальный порядок шагов, принадлежащих р-фрагменту. Штриховые стрелки указывают следование шагов, обуслов­ленное наличием специального порядка. Легко видеть, что шаг 2_αпредшествует шагу 1_β в первом частном процессе, а шаг 1 _α предшествует шагу 2_β в β-фрагменте. Таким обра­зом, шаг 2_α является предшествующим для шага 2_β. Но вместе с тем, аналогично рассуждая, мы убеждаемся, что также шаг 2_β предшествует шагу 2_α. Ясно, что первый процесс остановится перед тем, как выполнять шаг 2_α, а второй про­цесс остановится перед тем, как выполнять шаг 2_β.

При большем числе критических фрагментов и большем числе алгоритмов в коллективе возможны более сложные конфигурации абсолютных тупиков (клинчей).

3) Еще более интересное явление мы обнаруживаем, анализируя совокупные процессы, при наличии в них одно­именных «плавающих» критических фрагментов. Два одно­именных критических фрагмента (связанных с одним и тем же несобственным элементом) называются плавающими друг относительно друга, если в совокупном процессе нет нн одного частного процесса, который содержал бы крити­ческий шаг одного, предшествующий критическому шагу со специальным номером 0 другого из упомянутых фрагментов.

Имея дело с плавающими одноименными фрагментами, можно говорить о «захвате» одним из них соответствующе­го несобственного элемента, так как коль скоро один из них начал выполняться, то критические шаги остальных ока­зываются запрещенными и запрет будет снят не раньше» чем закончится выполнение фрагмента, захватившего не­собственный элемент. При этом запрещенные фрагменты мешают выполнению и регулярных шагов, расположенных в частных процессах между их критическими шагами. Удоб­но ввести термин (критическая) зона, понимая под ним совокупность всех шагов некоторого фрагмента и всех ос­тальных шагов, расположенных в частных процессах между шагами, принадлежащими фрагменту. Критическую зону, соответствующую α-фрагменту, будем коротко называть α -зоной. Как и фрагменты, зоны могут плавать друг отно­сительно друга.

В терминах плавающих критических зон нам не трудно пояснить механизм возникновения тупиков, связанных с явлением запрета. На рис. 19 схематически изображен со­вокупный процесс выполнения коллектива трех алгоритмов, в котором имеются две плавающие α -зоны и две плавающие β-зоны, причем 1-я α-зона пересекается с 1-й β-зоной, несколько предшествуя ей, а вторая α-зона пересекается со 2-й β-зоной, несколько отставая от нее. Области А и Б совокупного процесса, заштрихованные на схеме, играют особую роль. Если в обе эти области «вошли» частные про­цессы, то неминуемо наступает тупик. Если же одна из этих областей оказалась «пройденной» хотя бы одним процессом раньше, чем в другую «вошел» хотя бы один процесс, то ту­пик не наступит. При повторных применениях коллектива

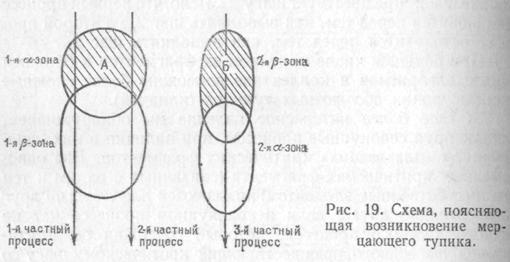
алгоритмов к одному и тому же исходному данному тупик может иногда возникать, а иногда может не возникать (в зависимости от не поддающихся учету воздействий, влияю­щих на соотношение скоростей протекания частных про­цессов). Такого рода тупики называются мерцающими.

Конфигурация мерцающего тупика может быть значи­тельно сложнее, чем описанная. Наконец, нужно иметь в виду, что тупики всех трех видов могут между собой соче­таться, создавая очень сложную картину.

Заканчивая наше краткое исследование коллективов ал­горитмов, заметим, что коллективы алгоритмов безусловно являются алгоритмами в интуитивном смысле, во всяком случае, если входящие в них одиночные алгоритмы не слиш­ком сложны. Но насколько объекты, изучаемые аналити­ческой теорией алгоритмов, сложнее тех избранных алго­ритмов, которые рассматриваются логическими теориями!

Заметим, что понятие коллектива алгоритмов является расширением понятия алгоритма. Одиночный алгоритм мож­но считать частным случаем коллектива (в котором n =1)-Значит такой «коллектив» может быть и открытым. Но как же с однозначностью? Для открытых коллективов однознач­ность надо понимать в обобщенном виде. Если исходным данным считать не только операнд, но совокупность операнда и тех последовательностей, члены которых вводились извне в несобственные элементы операнда, то результат окажется однозначно от них зависящим.