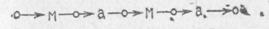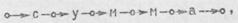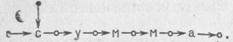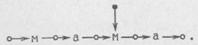Если мы хотим употреблять термин «язык программ», а это нам нужно, чтобы считать программы алгоритмами, мы должны допускать возможность очень сложной структуры предложений языка. Автор думает, что полезность трактовки программ для ЭВМ как алгоритмов уже не вызывает у читателя сомнений, и потому не будет второй раз ее обосновывать.
Читатель помнит, что программа, размещенная в машине, состоит из команд, среди которых присутствуют и команды перехода, причем связь между командами программы установлена с помощью команд перехода и определенного размещения команд в оперативной памяти. Все эти связи можно проследить и в программе, написанной на бумаге.
В последнем случае вместо особого способа размещения команд мы имеем (даже более наглядный) способ обозначения их связей с помощью собственных адресов (и, конечно, команд перехода).
Анализируя программы, мы видим, что основным строительным материалом для них являются символы (в теории алгоритмов мы их называли буквами). Из этих букв образованы более сложные конструкции (элементы кода программы: адреса и код операций), являющиеся словами. Эти слова объединены в системы, называемые командами. Причем даже в составе команды каждое из указанных слов сохраняет свою индивидуальность. Команды можно считать словами, о разделении которых на более простые слова задана информация. Но это неудобно, так как равносильно тому, что каждая команда имеет к себе «примечание». Лучше считать команду структурной, образованной не непосредственно из букв, а из более простых слов. Приказ имеет аналогичную, но еще более усложненную структуру. Наконец, программа на бумаге есть некоторая конструкция, образованная из приказов. Можно считать, что любая программа построена с помощью элементов трех видов: букв, связей, которые могут связывать буквы и еще некоторые другие объекты (чуть ниже мы их назовем), и оболочек, которые могут «облекать» (объединять в одно целое) конструкции, полученные с помощью связей из букв или из простых конструкций, заключенных в оболочки (именно эти объекты мы имели в виду несколько выше). Те объекты, которые могут быть связаны связями, будем называть конструктивными элементами. Таким образом, заключая некоторую конструкцию в оболочку, мы тем самым превращаем ее в конструктивный элемент, из которого можно образовывать более сложную конструкцию.
Приведенное описание несколько туманно. Сформулируем его более точно в виде следующих пунктов.
1. Конструктивным элементом является либо отдельная буква, либо конструкция, заключенная в оболочку.
2. Конструкцией называется либо пустое множество, либо несколько конструктивных элементов, связанных несколькими связями так, что «способности» связей к связыванию полностью использованы (связи насыщены), а любые два конструктивных элемента можно соединить цепочкой из конструктивных элементов и связей (конструктивные элементы связаны).
Нужно точнее пояснить, что мы понимаем под буквами,
оболочками и связями.
Буквы — это применяемые нами символы, которые в процессе их использования уже нельзя делить на части или как-либо деформировать.
Оболочки являются подобием скобок. По существу, открывающая и закрывающая скобки, рассматриваемые вместе, являются не чем иным, как оболочкой, облекающей некоторую строку символов. Нам пришлось пойти на такое видоизменение скобок в связи с тем, что среди конструкций мы будем допускать более сложные, чем цепочки букв или других конструктивных элементов.
Наконец, связи — это условные знаки, обозначающие взаимодействие между конструктивными элементами. Понятие связи так же естественно, как и понятие буквы. Связи мы постоянно наблюдаем, хотя до сих пор не говорили о них.
В слове «мама» присутствуют три вида связей, которые в своей совокупности образуют связи следования букв. В этом слове связи не изображены никакими символами. Они переданы особым расположением букв. Тем не менее они там есть. Если ввести символы для обозначения связей следования букв, обозначив их соответственно через  и
и  , то слово «мама» следует представить в виде
, то слово «мама» следует представить в виде
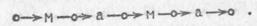
Здесь  означает «одноместную» связь, называемую начинающей, знак
означает «одноместную» связь, называемую начинающей, знак 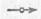 означает «двухместную» связь, называемую продолжающей.
означает «двухместную» связь, называемую продолжающей.
Наконец, знак  означает «одноместную» связь, называемую заканчивающей.
означает «одноместную» связь, называемую заканчивающей.
Однобуквенное слово «а» (союз) имеет вид: 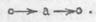
В нем нет продолжающих связей, но есть начинающая и заканчивающая.
Мы, говоря о связях, иногда будем их обозначать особыми знаками, иногда будем передавать особым способом расположения конструктивных элементов, но всегда будем иметь в виду их наличие.
Читателю следует обратить внимание на то, что, фиксируя и учитывая наличие связей, мы начинаем глубже понимать структуру предложении языка, начинаем в ряде случаев улавливать различия, которые без учета связей остаются незаметными. Например, буква «а» и слово 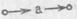 являются конструкциями различного вида. Не замечая связей, мы не замечаем и этого различия. В некоторых случаях подобное различие бывает существенным.
являются конструкциями различного вида. Не замечая связей, мы не замечаем и этого различия. В некоторых случаях подобное различие бывает существенным.
Кроме связей следования букв, нам очень знакомы (и одновременно очень незнакомы) многие другие связи. Например, введем обозначения  для начинающей, продолжающей и заканчивающей связи между словами. В фразе «Мама идет» присутствуют такие связи.
для начинающей, продолжающей и заканчивающей связи между словами. В фразе «Мама идет» присутствуют такие связи.
…
бы речь шла о наручниках, с помощью которых человека можно сковать сослоном. Здесь была бы связь второго ранга и второго жанра («ветви» связи были бы различны). Ремни, висящие во многих автобусах и предназначенные для того, чтобы стоящий пассажир во время движения за них держался, можно считать связями второго ранга и второго жанра. При этом одна ветвь «связывает» автобус, а другая «связывает» пассажира.
Итак, теперь мы имеем достаточно ясно представление о связях. Подчеркнем только еще раз, что если два конструктивных элемента связаны ветвями одинакового жанра какой-либо связи, то невозможно отличить, какая из ветвей соответствует любому из них. Обмен между ними одинаковыми ветвями не вызвал бы никаких перемен.
Оболочку можно считать особым видом буквы. Если некоторая конструкция заключена в оболочку, то удобно считать, что каждый конструктивный элемент этой конструкции связан некоторой связью с оболочкой. Эти связи мы для упрощения явно не указываем, но можем сказать, каковы они: они все одинаковы, так что оказать предпочтение тому или другому из конструктивных элементов они не позволяют. Кроме того, эти связи имеют второй ранг и второй жанр и всегда одинаково подключены к оболочке именно своими ветвями первого жанра.
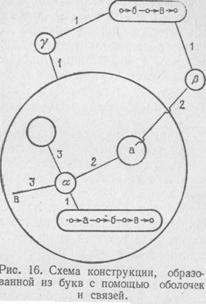
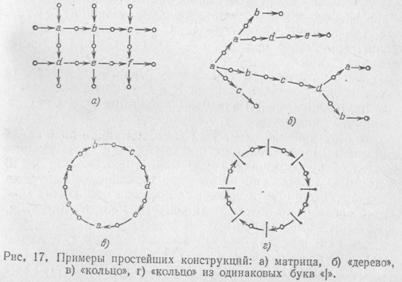
Если какой-либо конструктивный элемент является конструкцией, облеченной в оболочку, то связи, которые его связывают «в целом», своими ветвями «подключены» к его оболочке. Мы допустим расширение понятия конструкции, если скажем, что после того, как конструкция получена способом, описанным в ее определении выше, можно наложить на нее еще некоторое количество связей, «проникающих» сквозь оболочки ее конструктивных элементов на какую угодно глубину. То, что получится, снова будем называть конструкцией и допускать в качестве строительного материала для более сложных конструкций. Заметим только, что если все связуемые элементыкакой-либо связи находятся внутри некоторой оболочки, то считается, что она сама тоже находится внутри этой оболочки. На рис. 16 приведена схема конструкции, образованной из букв с помощью оболочек и связей. На этом рисунке α, β, γ— имена связей, кроме того, показаны связи следования букв, имена которых не обозначены. Замкнутые линии изображают собой оболочки. Одна из оболочек, связанная ветвью жанра 3 связи α, облекает собой пустую конструкцию. Связь β проникает ветвью второго ранга через две оболочки, На практике обычно встречаются менее замысловатые конструкции, чем показанная на рис. 16, например, «деревья» и «кольца», образованные с помощью связей следования из букв, матрицы и т. п. Эти виды конструкций пояснены на рис. 17.
В некоторых случаях удобно ограничить класс рассматриваемых конструкций. С этой целью задают алфавит букв, алфавит (перечень) связей и знак, являющийся обозначением оболочки. При этом алфавиты считают не только перечнями, но учитывают и порядок расположения в них перечисляемых элементов. Другими словами, алфавиты можно считать словами, но по отношению к «языку» рассматриваемых конструкций будем их считать метасловами (т. е. словами, принадлежащими метаязыку).
Условным обозначением класса конструкций является запись (А, В, Σ), в которой А — алфавит букв, В — алфавит связей, Σ — символ, говорящий о возможности применения оболочек. В конкретных случаях вместо А и В могут быть записаны в виде слов конкретные алфавиты, а символ Σ всегда будет включаться без всякой конкретизации.
§ 4. Формальные грамматики
Вернемся к описанию языков. Считается, что предложениями языков могут быть любые конструкции, описанные в предыдущем параграфе. Уже одним этим расширяется понятие языка. Как уже сказано, синтаксис языка не должен зависеть от его семантики. Термин «предложение» сохраним и для формальных языков. Мы не накладываем запретов ни на какие формы синтаксиса, но для того чтобы всегда быть уверенными в том, что мы располагаем именно формальным языком, потребуем, чтобы существовала (т. е. могла бы быть построена) формальная грамматика, имеющая определенную каноническую форму. Американский лингвист А. Хомский предложил следующую форму грамматики. Для описания синтаксиса языка-объекта задается алфавит букв этого языка, затем алфавит вспомогательных символов, называемых нетерминальными (буквы первого алфавита при этом называют терминальными символами), затем — конечный набор синтаксических правил и, наконец, однобуквенное слово, образованное из нетерминального символа. Условно это передают в виде обозначения (А, С, R, σ), где А — алфавит языка-объекта, С — нетерминальный алфавит, R — набор правил, σ — указанная выше нетерминальная буква.
Каждое правило в грамматике Хомского имеет вид подстановки Р → Q, в которой Р и Q — слова в алфавите АС (получающемся соединением алфавитов А и С). Подстановки, применяемые А. Хомским, не являются марковскими подстановками (см. § 3 гл. 4) и вообще не являются однозначными операциями преобразования конструкций. Объектом преобразования для таких подстановок могут быть только слова, но применение подстановки допускает произвол. Если преобразуемое слово имеет несколько вхождений слова Р, то подстановка допускает замену любого из этих вхождений правой частью формулы.
Так как, вообще говоря, число вхождений Р в разные слова неограниченно, то можно считать, что каждая подстановка представляет собой бесконечное множество операций замены словом Q: 1) первого вхождения P; 2) второго вхождения Р;...; п) п -го вхождея P и т.д.Выполнение подстановки заключается в выполнении произвольной операции из перечисленных. Однако подстановку можно рассматривать и как конечное множество определенных операций, выполняемых в различных сочетаниях. Дальнейшее изучение подстановок мы производить не станем, поскольку эта проблема для нас особого интереса не представляет. Разъясним только способ порождения формального языка с помощью грамматики Хомского. Предложение языка получим, если применим к однобуквенному слову σ одну из подстановок. Если результат не содержит нетерминальных символов, предложение языка уже получено; если же содержит, то применяем опять одну из подстановок, и т.д. Говорят, что предложение языка выводится из начального слова σ с помощью правил, входящих в состав R, - набора синтаксических правил грамматики Хомского. Аналогично выводится другое предложение и т.д. Грамматики Хомского нас не удовлетворяют по друм причинам. Во-первых, их возможности слишком ограничены, так как с их помощью можно построить только язык, предложениями которого являются слова. Во-вторых, способ порождения языка, избранный Хомским, является слишком искусственным и для нас непривычным. Ни одна знакомая нам грамматика ни одного из естественных языков не имеет вида грамматики Хомского. Обычно предложения языка строят из более простых конструкций и в конце концов все предложения получаются из некоторых элементарных конструкций, называемых морфемами. Остановимся и мы на такой форме порождающих грамматик.
Предположим, что заданы алфавиты букв и связей и знак оболочек, из которых будут построены предложения языка-объекта, т.е. считаем, что известен класс (A, B, Σ) конструкций, с которыми нам придется иметь дело при построении языка. Далее, допустим, что задано конечное число простейших конструкций, множество которых назовем базой языка и обозначим буквой Б. Элементы этого множества называются морфемами. Предположим, что задан алфавит С символов, с помощью которых записываются синтаксические правила. Эти правила у нас всегда будут иметь вид цепочек из символов, т.е. слов. Поэтому специально оговаривать наличие алфавита связей, нужного для записи правил, мы не станем. Алфавит С должен содержать символы четырех видов, попарно различные между собой и не совпадающие с символами, участвующими в конструкциях класса (A, В, Σ). Символы первого вида применяются как индивидуальные имена морфем. Символы второго вида будем применять в качестве групповых имен получаемых конструкций. Символы третьего вида играют роль функциональных знаков и являются именами операций. Наконец, символы четвертого вида играют вспомогательную роль: это скобки, запятые, знаки равенства и знаки «точка с запятой» или заменяющие их символы.
Каждое синтаксическое правило будет иметь либо вид
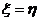 ,
,
где η— имя морфемы, ξ — групповое имя, либо вид
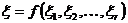 ,
,
где ξ — групповое имя, ξ1, ξ2, …, ξr —- групповые имена или имена морфем, f — функциональный знак, r — ранг операции, именем которой является f.
Рангом операции называется число величин, которые участвуют в качестве исходных данных при выполнении операции. Например, среди известных нам операций lg x — операция первого ранга, sin х и  — тоже; х + у и х: у — операции второго ранга. Можно считать, что выражение x+y*z задает некоторую операцию третьего ранга.
— тоже; х + у и х: у — операции второго ранга. Можно считать, что выражение x+y*z задает некоторую операцию третьего ранга.
Будем считать, что грамматика задана, если заданы все перечисленные алфавиты, база языка и набор синтаксических правил описанного вида, а также выделено одно из групповых имен (буква), играющее роль группового имени всех конструкций, являющихся предложениями языка. Такую грамматику будем называть индуктивной порождающей грамматикой, в отличие от грамматик, подобных грамматикам Хомского, в которых предложения языка выводятся из слова о и которые поэтому можно назвать дедуктивными.
Итак, индуктивная грамматика задана, если указан класс конструкций (А, В, Σ), подмножеством которого является определяемый язык, база Б языка, являющаяся конечным подмножеством этого класса, алфавит С для записи синтаксических правил, набор R синтаксических правил и буква σ, являющаяся групповым именем предложений языка.
Порождение предложений языка осуществляют так: выбирают несколько формул, в правых частях которых стоят имена морфем. С помощью этих правил придают значение некоторым групповым именам (стоящим в указанных формулах слева от знака равенства). Затем произвольно выбирают формулы, для которых групповые имена, стоящие в правых частях, уже имеют значения; над этими значениями выполняют операции, указанные в формулах; процесс продолжают до тех пор, пока в левой части применяемой формулы не окажется буква σ. Полученная при этом конструкция, являющаяся значением имени σ, является одним из предложений языка. Процесс может на этом закончиться (если мы того желаем) или продолжиться далее, если имеется правило, в правой части которого присутствует буква σ. Тогда он будет продолжаться до тех пор, пока в левой части применяемой формулы не встретится снова символ σ, и т. д.
Если для какого-либо языка построена некоторая порождающая грамматика индуктивного типа, то будем говорить, что данный язык (без учета семантики) является формальным. В теории формальных языков доказана следующая теорема.
Теорема. Любой язык, порождаемый грамматикой Хомского, является формальным языком (без учета семантики), т. е. для такого языка всегда можно построить индуктивную порождающую грамматику.
Интересно отметить следующую теорему.
Теорема. Конечное множество различных между собой предложений естественного языка является формальным языком (без учета семантики), т. е. для него можно построить грамматику индуктивного типа.
Доказательство этой теоремы очень просто, а ее результат имеет большое практическое значение. Приведем это доказательство. Предположим, что нам задано конечное множество предложений естественного языка, например, в виде списка. Пусть это будут Р1, Р2, …, PN. Просматривая эти предложения, мы можем отобрать все буквы, присутствующие в них; в число букв в общем случае попадут и знаки препинания, и пробелы. Перечень этих букв будет искомым алфавитом А. Связи следования составят алфавит В. Алфавит С образуем из букв «;», «=», «а» и всех символов Р1, Р2, …, PN (считаем, что они отличаются от букв в А, друг от друга и от букв «;», «=», «а»). Теперь напишем N синтаксических правил:
σ = Р1; σ = Р2; …; σ = PN.
Базой считаем совокупность предложений, обозначенных символами Pi. Читатель видит, что индуктивная грамматика построена и, следовательно, конечное множество предложений естественного языка является формальным языком (без учета семантики).
Прием построения формального языка путем составления перечня предложений является простейшим случаем так называемой формализации естественного языка. При.! этом, отбирая предложения, необходимо следить за тем, чтобы каждое из них обладало единственным смыслом; мы, получим формальный язык, наделенный семантикой.
Обратим внимание на сам способ задания языка, примененный в данном случае: язык представлен в виде перечня предложений, оформленных как список. Такой список является частным случаем таблицы. Возможны более сложные таблицы, задающие формальные языки. Об одной из них — тезаурусе — мы расскажем в следующем параграфе.
Мы познакомились с табличной формой задания формального языка. Табличная форма с успехом используется для построения формальных языков, применяемых при описании исходных данных многих задач, решаемых на ЭВМ (в тех случаях, когда эти исходные данные не являются числами).
Нотация Бекуса. Тезаурусы
В 1958 г. на русский язык было переведено описание алгоритмического языка лгол-58, составленное с помощью особых синтаксических правил, получивших название формул Бекуса. Способ описания формального языка с помощью формул Бекуса называется нормальной формой или нотацией Бекуса.
Рассмотрим частный случай порождающей индуктивной грамматики, в котором применяемыми конструкциями являются слова, а операциями, имена которых присутствуют в синтаксических правилах, являются так называемые операции соединения слов. Обозначим эти операции временно символами S1(P), S2(P1, Р2), S3(P1, P2. P3), …, Si(P1, Р2, ..., Pi), где Р, P1, Р2,..., Рi — произвольные слова. Сущность этих операций заключается в следующем. Операция S1(P) является тождественной операцией. Для нее справедливо равенство
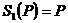 .
.
Например S1(мама)=мама.
Для операции S2(P1, P2) справедливо условие
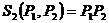 .
.
т. е. ее результатом является новое слово, получаемое путем приписывания елов Р2 к слову Р1. Например, S2 (экстра, алгоритм) = экстраалгоритм.
Вообще, для Si(P1, P2, …, Рi) справедливо условие
Si(P1, P2, …, Pi)=P1P2…Pi.
В описанном частном случае запись синтаксических правил индуктивной грамматики можно видоизменить (не изменяя их смысла) следующим образом.
1. Во всех синтаксических правилах знак «=», отделяющий левую часть от правой, заменим знаком «:: =», который читается как «по определению есть».
2. Во всех правилах имена морфем заменим самими морфемами. Это можно сделать, так как морфемы являются словами (пустыми, однобуквенными или многобуквенными).
3. Если имеется несколько формул, в левых частях которых стоят одинаковые групповые имена, то заменим эти несколько формул одной, имеющей такую же левую часть, а в правой части содержащей записи всех правых частей указанных формул, разделенные знаками «|». Эти знаки читаются как «или». Данное видоизменение синтаксических формул не обязательно. Новая формула рассматривается как сокращенная запись вошедших в нее старых формул.
4. Пользуясь тем, что результат выполнения операции Si соединения можно получить из ее записи путем отбрасывания функциональной буквы Si, скобок и разделяющих аргументы запятых, отбросим в правых частях синтаксических правил знаки Si, знаки «(», «)», «,».
5. Наконец, условимся об особом выборе символов, являющихся групповыми именами. В качестве таких символов будем брать фразу на естественном языке, заключенную в угловые скобки. Такая фраза в угловых скобках является одним целым и неизменяемым знаком — метасимволом.
Заметим, что в языке-объекте и в используемом естественном языке не должны применяться буквы «:: =», «|». «<«, «>» или сочетания букв, одинаковые с символом:: =,
Полученная нами совокупность синтаксических правил и составляет нотацию Бекуса, а каждое правило называется формулой Бекуса.
Приведем пример описания формального языка с помощью нотации Бекуса. Ставить внутри формул знаки переноса или после них знаки препинания нельзя!
Как известно, десятичная система счисления является формальным языком. Ее алфавит содержит десять букв, обычно называемых арабскими цифрами. Будем считать, что базу языка составляют десять морфем, каждая из которых является однобуквенным словом. Для обозначения группового имени «морфема» используем метасимвол «(цифра)». Итак, приводим формулы Бекуса:
<ненуль>::= 1|2|3|4|5|6|7|8|9
<цифра>::=0 | <ненуль>
<строка цифр>::= <цифра> | <строка цифр> <цифра>
<неотрицательное целое число>::= <цифра> | <ненуль>
<строка цифр>
Эти четыре формулы Бекуса дают полное описание десятичной системы счисления. Покажем, как с помощью этих формул можно порождать различные записи чисел. В силу первой и второй формул 1, 2, 7, 0 являются цифрами. В силу третьей формулы 001207 является строкой цифр, а в силу второй формулы 5 является ненулем. Наконец, в силу четвертой формулы 5001207 является неотрицательным целым числом.
Формулы Бекуса очень удобны для описания формальных языков. Но, к сожалению, они пригодны только для языков, предложениями которых являются конструкции, называемые словами. Кроме того, даже среди таких языков они пригодны далеко не для всяких.
Есть очень простые слова, которые невозможно описать с помощью формул Бекуса. Например, к их числу относятся «спаренные числа»; чтобы написать такое число, нужно сперва написать какое угодно число, а затем к нему приписать в точности такое же число. Спаренными числами являются 88, 9191, 235235 и т. п. К сожалению, формула Бекуса
<спаренное число>::= <неотрицательное целое число> <неотрицательное целое число>
не является описанием спаренных чисел, так как наряду со спаренными числами дает и многие другие.
Несмотря на ограниченные возможности нотации Бекуса, она настолько удобна, что ею довольно часто пользуются. Мы с вами, читатель, тоже будем ее применять и потому постараемся ее запомнить. Вот еще пример описания с ее помощью несложного языка:
<цифра>::=0|1|2|3|4|5|6|7|8|9
<буква> ::=А|В|C|D|E|F|G|Н|I|J|K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z
<идентификатор>::= <буква> | <идентификатор> <буква> | <идентификатор> <цифра>
С помощью указанных трех формул определена синтаксическая структура, называемая идентификатором. В ряде языков программирования такие конструкции применяются в качестве имен переменных величин и некоторых других элементов программ.
В конце предыдущего параграфа мы говорили о том, что конечное множество предложений естественного языка представляет собой, без учета семантики, формальный язык. Такой формальный язык можно описать с помощью формул Бекуса. Еще один вид его описания называют тезаурусом; его мы упоминали в предыдущем параграфе[23]. В простейшем случае тезаурус — это список упомянутых предложений. В более сложном случае тезаурус представляет собой перечень некоторых текстов, каждому из которых придана дополнительная, так называемая грамматическая информация. Эта структура тезауруса применяется в тех случаях, когда список предложений очень велик. Мы поясним его на небольшом списке, чтобы передать только самую суть этого способа описания формального языка.
Представим себе, что множество предложений естественного языка содержит такие фразы, как: текстильное производство, текстильная фабрика, текстильное изделие, текстиль, ткань, токарный станок, токарная работа и т. д. В тезаурус можно включить тексты, разбив их на группы и указав между ними связи (см. табл. 7).
Таблица 7

Чтобы получить предложения языка, нужно войти в тезаурус. Если мы остановимся на позиции 1, то прочитаем текст «изделие» и узнаем, что с ним связана позиция 10. В позиции 10 прочитаем текст «текстильн» и информацию* 21 —1,2, которая означает, что за «текстильн» следует содержимое позиции 21 и затем текст «изделие» (цифра 1 во второй части информации).
В итоге получаем предложение «текстильное изделие».
Знак  означает пробел. Знак * означает «данный текст» (в этом примере «текстильн»). Числа означают номера позиций. Если два числа разделены запятой, то из них должно быть выбрано то, которое является номером позиции, от которой был совершен переход к данной позиции. В графе «смысловые связи» у нас указана лишь подчиненность понятий. Запись «2>3» значит, что понятие «производство» старше понятия «работа».
означает пробел. Знак * означает «данный текст» (в этом примере «текстильн»). Числа означают номера позиций. Если два числа разделены запятой, то из них должно быть выбрано то, которое является номером позиции, от которой был совершен переход к данной позиции. В графе «смысловые связи» у нас указана лишь подчиненность понятий. Запись «2>3» значит, что понятие «производство» старше понятия «работа».
Под номером 5 в тезаурусе стоят 2 термина «текстиль» и «ткань». Эти термины считаются синонимами (что, собственно, относится уже к смысловым связям).
Реально применяемые тезаурусы могут быть значительно сложнее того, который описан в качестве примера. В тезаурусе, кроме указанных сведений, нередко содержатся «отсылки» к массивам информации и программам, позволяющим получить «смысловую» информацию, связанную с текстами, включенными в тезаурус.
Логическая теория алгоритмов ограничивается языками, предложения которых, как символьные конструкции, являются словами. При этом можно учитывать только буквы, не упоминая о связях. Однако это ничего не упрощает, потому что предполагает у человека наличие способностей опознавания слов, расчленения их на буквы, что порождает опасность разночтения, и преобразования всевозможных символьных конструкций в слова (и обратно). Правда, иногда переход к словам не очень труден. Например, любой типографский текст превращается в слово, если к классу букв отнести все литеры, включая и пробелы.
Привлекая связи и допуская символьные конструкции большой сложности, аналитическая теория алгоритмов предъявляет меньшие требования к неформальным способностям человека, хотя и приводит к кажущемуся усложнению понятия формального языка.
Г л а в а 8
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ТЕОРИИ
АЛГОРИТМОВ
§ 1. Что такое операция?
В предыдущей главе, при определении понятия формальной грамматики, было использовано понятие операции, а в параграфе, посвященном нотации Бекуса, применялись конкретные операции: операции соединения слов.
Понятие операции тесно связано с понятием алгоритма, и поэтому следует считать, что в гл. 7 мы «забежали» вперед. В этом нет беды. Можно считать, что мы пока условно определили понятие формальной грамматики (а значит, и порождаемого ею языка). После точного разъяснения смысла слова «операция» станет точным и строгим это «условное» определение.
Уже в самом начале гл. 1 было сказано о некоторых операциях, выполняемых в соответствии с требованиями алгоритма. Но тогда еще точный смысл этого слова был не нужен. Если никак не ограничить смысл слова «операция», то останется неясным и смысл слова «формальный язык»
и слова «алгоритм».
Итак, что же такое операция? Исходным данным для операции может быть либо отдельная конструкция (при этом говорят, что операция имеет первый ранг), либо набор, образованный из конструкций (в этом случае говорят, что операция имеет ранг г). Принято считать, что каждая операция имеет постоянный, всегда один и тот же ранг. Кроме того, положим, что операция однозначна. Каждому исходному данному она ставит в соответствие единственный
определенный результат.
Мы будем допускать два вида операций: простейшие, основные операции, определение которых не входит в компетенцию теории алгоритмов, и более сложные, «производные» операции, получаемые методами теории алгоритмов. Простейшие операции назовем натуральными. Каждая из них должна быть тщательно разъяснена. Понятие производной операции свяжем с расширенным понятием алгоритма.
Итак, операциями будем называть либо натуральные операции, либо объявленные операциями и получившие обозначения отображения исходных данных на искомые результаты, для реализации которых существуют (уже получены) алгоритмы.
Это определение требует, чтобы каждый раз, когда нужна новая операция, сначала был построен определяющий ее алгоритм, затем совершен акт ее объявления операцией и, наконец, в некотором формальном языке присвоено ей имя.
Объявление новой операции является абстрактным аналогом следующей конкретной ситуации. В реальной жизни очень часто, имея некоторую машину, разрабатывают для нее определенную программу. При эксплуатации этой программы убеждаются, что ее приходится очень часто применять. Тогда разрабатывают новую ЭВМ, в которой ранее полученная для старой ЭВМ программа реализована уже аппаратурно и новой машиной выполняется за один такт. Еще один убедительный пример объявления новой операции в реальной практической области приведем позже, когда познакомимся с математическим обеспечением ЭВМ.
Натуральные операции
Прежде чем описывать конкретные натуральные операции, нужно поговорить о возможных исходных данных и результатах.
К первой группе отнесем натуральные операции, исходными данными для которых являются слова или наборы слов, а результатами — отдельные слова. Группу этих операций назовем группой слово-слово.
В эту группу войдут четыре следующие операции.
1. Аннигиляция. Сущность аннигиляции состоит в том, что если ее применить к однобуквенному слову, то в качестве результата будет получено пустое слово. К многобуквенным словам эту операцию применить нельзя. Для таких исходных данных она не определена и никакого результата не дает. Для обозначения аннигиляции введем знак 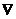 .
.
2. Генерация противоположна аннигиляции. Эта операция применима к пустому слову и в качестве результата дает однобуквенное слово. Но различных однобуквенных слов столько же, сколько различных букв. Поэтому операций такого вида много. Если αнекоторая буква, то ей отвечает так называемая α -генерация. Для такой операции введем обозначение hα. К непустым словам α-генерация неприменима и для них никакого результата не дает.
3. Одноместная операция соединения слов (описана в § 5 гл. 7). Будучи применена к произвольному слову, эта операция в качестве результата дает то же слово. Эту операцию будем обозначать S1(P), где P — слово.
4. Двухместная операция соединения слов (описана в § 5 гл. 7). Эта операция, будучи применена к упорядоченному набору из двух слов, в качестве результата дает слово, которое получится, если к первому слову (после его конца) приписать второе слово. Эту операцию обозначим S2(P1, Р2), где P1 и Р2 — слова.
Ко второй группе натуральных операций, называемой группой слово-квазислово, отнесем операции, для которых исходными данными являются слова, а результатами — квазислова (см. ниже), и операции, для которых исходными данными являются квазислова, а результатами — слова.
Квазисловом будем называть конструкцию, отличающуюся от слова тем, что одна из ее букв связана дополни тельной связью первого ранга, которая отличается как от начинающей, так и от заканчивающей связи следования и называется выделяющей связью. Поясним понятие квазислова примерами. Слово «мама» имеет структуру
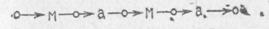
Из этого слова можно получить четыре различных квазислова:

Таким образом, квазислово — это слово с одной выделенной в нем буквой. В обыденной жизни, имея слово и рассматривая в нем определенную его букву, мы фактически имеем дело с квазисловом.
В группу слово-квазислово входят следующие две операции.
5.Нахождениеначала слова. Обозначим чту операцию символом * (звездочка). Она применима к любому непустому слову и преобразует его в квазислово, в котором выделена начальная буква. К пустому слову эта операция неприменима и для него не дает никакого результата. Если применить операцию нахождения начала к слову
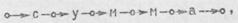
то результатом будет квазислово
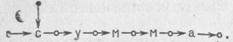
6. Отключение — операция, противоположная предыдущей. Она применима к любому квазислову и в качестве результата дает соответствующее ему слово. Иными словами, эта операция уничтожает в квазислове выделяющую связь и тем самым превращает его в обычное слово. Обозначим эту операцию знаком X. Эту операцию мы производим, когда в рассматриваемом слове перестаем особо рассматривать одну из его букв.
Третья группа операций называется квазислово-квазислово. В нее входит пять натуральных операций.
7. Операция продвижения вправо. Обозначим ее символом →. Заключается она в том, что от заданного квазислова она ведет к квазислову, в котором выделена буква, непосредственно следующая за той, которая была выделена в исходном данном. Например, применяя продвижение вправо к квазислову
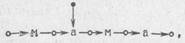
получим квазислово
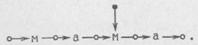
К квазислову, в котором выделена последняя буква (или, образно говоря, в котором рассматривается конец), эта операция неприменима и для него никакого результата не дает.
8. Операция продвижения влево; обра





 и
и  , то слово «мама» следует представить в виде
, то слово «мама» следует представить в виде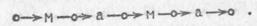
 означает «одноместную» связь, называемую начинающей, знак
означает «одноместную» связь, называемую начинающей, знак 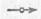 означает «двухместную» связь, называемую продолжающей.
означает «двухместную» связь, называемую продолжающей. означает «одноместную» связь, называемую заканчивающей.
означает «одноместную» связь, называемую заканчивающей.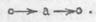
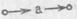 являются конструкциями различного вида. Не замечая связей, мы не замечаем и этого различия. В некоторых случаях подобное различие бывает существенным.
являются конструкциями различного вида. Не замечая связей, мы не замечаем и этого различия. В некоторых случаях подобное различие бывает существенным. для начинающей, продолжающей и заканчивающей связи между словами. В фразе «Мама идет» присутствуют такие связи.
для начинающей, продолжающей и заканчивающей связи между словами. В фразе «Мама идет» присутствуют такие связи.

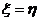 ,
,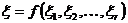 ,
, — тоже; х + у и х: у — операции второго ранга. Можно считать, что выражение x+y*z задает некоторую операцию третьего ранга.
— тоже; х + у и х: у — операции второго ранга. Можно считать, что выражение x+y*z задает некоторую операцию третьего ранга.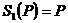 .
.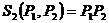 .
.
 означает пробел. Знак * означает «данный текст» (в этом примере «текстильн»). Числа означают номера позиций. Если два числа разделены запятой, то из них должно быть выбрано то, которое является номером позиции, от которой был совершен переход к данной позиции. В графе «смысловые связи» у нас указана лишь подчиненность понятий. Запись «2>3» значит, что понятие «производство» старше понятия «работа».
означает пробел. Знак * означает «данный текст» (в этом примере «текстильн»). Числа означают номера позиций. Если два числа разделены запятой, то из них должно быть выбрано то, которое является номером позиции, от которой был совершен переход к данной позиции. В графе «смысловые связи» у нас указана лишь подчиненность понятий. Запись «2>3» значит, что понятие «производство» старше понятия «работа».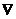 .
.