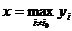§ 1. Арифметизация математики
Одна из причин, побудивших заняться теорией алгоритмов, нам уже известна. Это — «подозрительность» математиков в связи с накоплением упорно не поддающихся решению задач на нахождение алгоритмов. О второй причине читатель узнает в данной главе.
Еще древнегреческий математик Пифагор (580—500 гг. до н. э.) ввел ныне общеизвестный дедуктивный метод, сущность которого заключается в том, что из небольшого числа исходных утверждений, называемых аксиомами и принятых без доказательства, все остальные утверждения математики выводятся с помощью правил логики. Первым дошедшим до нас письменным документом, содержащим изложение одной из ветвей математики (геометрии) с помощью дедуктивного метода, является знаменитый труд Евклида (III в. до н. э.) «Начала». С тех пор постепенно математика по своей структуре стала противоположна всем другим естественнонаучным дисциплинам, имеющим эмпирический характер.
До середины XIX столетия никто не сомневался в истинности математических результатов, залогом чего считали истинность аксиом и правильность рассуждений, построенных по законам логики. Исследования Н. И. Лобачевского, Л. Бойаи и Б. Римана показали, что аксиомы нельзя считать истинами, не требующими доказательства. Собственно, и до этого одну из аксиом Евклида (пятую, утверждающую, что через точку, лежащую вне прямой, можно провести одну и только одну прямую, параллельную данной) многие математики считали не столь очевидной, как другие аксиомы[10]. Было предпринято немало попыток доказать эту аксиому как теорему, опираясь на другие, но безуспешно. Такую же попытку предпринял и Н. И. Лобачевский. Его идея состояла в том, чтобы заменить пятую аксиому противоположным ей утверждением[11] и прийти в результате этого к противоречию (доказательство от противного). Вместо противоречия была получена новая геометрия, известная теперь под названием геометрии Лобачевского.
Упомянутые исследования геометрии интересны сами по себе, но особенно они важны тем, что сокрушили веру в истинность аксиом и заставили задуматься над тем, что же является фундаментом математики. После того как Р. Декарт открыл метод координат, стали думать, что таким фундаментом может служить арифметика. Метод координат позволил геометрические объекты представить с помощью чисел. Например, точку плоскости можно рассматривать как пару чисел (являющихся ее координатами при некотором выборе системы координат). Прямую можно определить, указав какие-нибудь не совпадающие между собой две точки, лежащие на этой прямой (две пары чисел), и т. п. При таком подходе все геометрические утверждения могут быть пересказаны в виде утверждений о некоторых системах чисел.
При этом оказалось, что нет надобности отдельно рассматривать натуральные числа, целые отрицательные числа, дроби, действительные числа, комплексные числа. Можно свести все вопросы к рассмотрению только натуральных чисел и некоторых отношений между ними. Например, дробь можно рассматривать как совокупность числителя и знаменателя, т. е. как пару натуральных чисел, определенным образом связанных. Так, дробь 2/3 будет обозначаться (2,3), где скобки указывают на наличие упомянутого отношения. Относительные числа можно тоже рассматривать как лары натуральных чисел таких, что разность между первым и вторым элементами пары равна изображаемому этой парой числу. Например, числа 0, 5 и —5 можно представить в виде пар ((2,2)), ((7,2)) и ((3,8)) и т. д. Мы не будем подробнее останавливаться на приемах, позволяющих любые числа изображать в виде систем натуральных чисел. Заметим только, что эти приемы позволяют и геометрию пересказать в терминах натуральных чисел. Такое сведение различных теорий чисел и геометрии к теории натуральных чисел (т. е. арифметике) называется их арифметизацией. Была также доказана возможность полной арифметизации математического анализа и теории функций. Известный французский математик Ж. Пуанкаре на Втором международном математическом конгрессе даже заявил: «Теперь в математике остаются только целые числа и конечные или бесконечные системы целых чисел. Математика полностью арифметизирована ».
Возможность арифметизации вовсе не означает отказ от всех других понятий математики, а лишь убеждает нас в том, что фундаментом математики может служить арифметика.
Теория множеств
В результате арифметизации многие математические понятия выражаются через различные системы натуральных чисел, которые могут быть и бесконечными. Например, произвольное действительное число нельзя представить в виде конечной системы натуральных чисел. Чтобы в этом убедиться, достаточно рассмотреть общеизвестное я (отношение длины окружности к ее диаметру). При очень грубых расчетах берут вместо я десятичное число 3,14. Но при более точных расчетах нужно брать более близкое к нему десятичное число, скажем, 3,141592653, которое, однако, тоже не равно самому л. Короче говоря, п можно рассматривать только как бесконечное множество натуральных чисел, например, как последовательность натуральных чисел, соответствующих его цифрам, сохраняющимся при переходе к все более и более точным приближениям.
Разработанная немецким математиком Г. Кантором в 1874—1897 гг. теория множеств оказалась той научной дисциплиной, которая давала единые методы для изучения конечных и бесконечных систем предметов.
Основным объектом этой теории является множество. Говорят, что понятие множества относится к числу простейших и может быть только разъяснено, но не определено. Можно говорить о множестве людей, находящихся в некотором помещении, о множестве звезд в галактике, называемой Млечным Путем, о множестве букв, составляющих данную строку, о множестве натуральных чисел и т. п. Предметы, входящие в состав множеств, называются их элементами. Теория множеств изучает те свойства множеств, которые не зависят от свойств их элементов.
На первый взгляд, понятие множества кажется очень естественным и действительно простым. В своей практике люди испокон веков имели дело с различными множествами конкретных, а иногда и абстрактных предметов. Например, пастухи имели дело со стадами, строители — с кучами песка, охотник — с лесами, математики — с бесконечным рядом натуральных чисел. Но понятие множества в теории множеств столь обще и абстрактно, что из него выводимы все понятия математики.
Здесь автор позволит себе совсем немного пофилософствовать. В результате многовекового естественного отбора нервная система человека и высших животных сложилась так, что окружающий мир воспринимается ею как состоящий из отделенных друг от друга предметов. Это свойство нервной системы целесообразно и экономно. Благодаря ему животные, располагающие сравнительно простой нервной системой, находят пищу и спасаются от нападений других животных. Это свойство было унаследовано и человеком, от его животных предков. Понадобились века и тысячелетия для того, чтобы люди узнали, что в действительности мир более сложен, чем воспринимаемая ими совокупность предметов. В то же время разделение мира на предметы в какой-то мере отражает его объективные закономерности. Наш язык настолько приспособлен к выражению различных суждений именно о предметах, что автор испытывает определенные затруднения, стараясь объяснить существо понятия «предмет», не пользуясь для этого тем же понятием.
Восприятие мира как системы предметов связано с определенным актом абстрагирования, совершаемым нашей нервной системой бессознательно. Это абстрагирование имеет две стороны: 1) слабые влияния частей предмета на другие предметы (и их определенные части) либо не обнаруживаются (остаются незамеченными, как бы не переступают порога чувствительности нашего организма), либо не учитываются; 2) более сильные влияния частей предмета принимаются за влияние всего предмета в целом; при этом они либо суммируются, либо осредняются.
Сказанное можно пояснить вульгарным примером. Встречая определенного человека, я его воспринимаю как некоторый «предмет», влияние которого на меня заключается в том, что он мне что-то говорит и как-то действует, например, пожимает мне руку, если мы друзья, или наносит мне удар, если мы боксеры на ринге. Но мои чувства не воспринимают многих «частей» этого конкретного «предмета», например, наличия в его организме гриппозного вируса и влияния этого «предмета» на меня, заключающегося в том, что его органы дыхания выделяют этот вирус, и в результате контакта с этим «предметом» я заражаюсь гриппом.
Абстракцию, в результате которой некоторая часть мира признается нами за отдельный предмет, будем называть абстракцией предмета.
Познавая внутреннее строение предметов и их взаимодействие между собой и другими частями мира, мы каждый раз снова и снова совершаем эту же абстракцию, по отношению к более «мелким» частям мира.
Понятие множества связано с новой абстракцией. Объединяя предметы в множество и создавая тем самым новый предмет, мы игнорируем все свойства множества, зависящие от свойств входящих в него предметов, кроме свойств отличаться от всех других множеств, если в нем есть хотя бы один элемент, не содержащийся в другом множестве, или если в нем нет хотя бы одного элемента, присутствующего в другом множестве. Далее, мы не учитываем никаких связей между элементами и влияний их друг на друга, сохраняя за ними только свойство быть самостоятельными, различными между собой. Зато считается, что каждый элемент связан с содержащим его множеством отношением включения или, если угодно, связью включения, чего в действительности может и не быть. Это отношение в математике обозначают символом  . Запись а
. Запись а  А означает, что а является элементом множества А, входит в это множество.
А означает, что а является элементом множества А, входит в это множество.
Наряду с игнорированием влияния свойств элементов на свойства множества, теория множеств разрешает приписывать каким угодно предметам свойство быть элементами некоторого множества. Например, наша точка зрения на звезды как на предметы не дает нам никаких указаний на наличие каких-либо связей между звездами первой величины, которые позволили бы их объединить в один предмет. Тем не менее рассмотрение множества звезд первой величины вполне допустимо. Точно так же не вызывает возражений множество находящихся на земле людей, у которых на правой руке почему-либо нет указательного пальца, или множество собак, у которых отрублены хвосты, и т. п.
При объединении каких-либо элементов в множество требуется, чтобы эти элементы отличались друг от друга, но вовсе не считается необходимым, чтобы они существовали одновременно. Никакого возражения не вызывает, например, множество трех объектов пространства-времени, первым из которых является автор данных строк, существовавший вчера, вторым — он же сегодня, а третьим — он завтра. Сами множества тоже могут быть элементами новых множеств.
Как видит читатель, абстракция множества совершенно отлична от абстракции предмета. На этом наше философское отступление кончается.
Идея множества была, конечно, известна и до Г. Кантора. Г. Кантор нашел способ сравнивать между собой множества. Избранный им способ сравнения двух множеств заключается в установлении взаимно однозначного соответствия между их элементами. Этот способ представляет собой как бы объединение элементов одного множества в пары с элементами другого множества, причем так, что каждый элемент входит в одну-единственную пару.
Если для множеств А и В удается осуществить взаимно однозначное соответствие, то по определению эти множества равномощны. Для конечных множеств их рав-номощность означает, что они имеют одинаковые количества элементов.
Равномощность множеств нельзя смешивать с их равенством. Множества называются равными, если каждый элемент одного из них является также элементом и другого. Например, если за обеденным столом собрались все члены вашей семьи и нет никого постороннего, то можно утверждать, что множество людей, собравшихся за столом, и множество людей, являющихся членами вашей семьи, равны. Конечно, они и равномощны. Но некоторые равно-мощные множества никак нельзя признать равными. К их числу, например, относятся какое-либо множество из пяти людей и какое-либо множество из пяти собак.
Ради удобства вводится понятие пустого множества, т. е. множества, не содержащего ни одного элемента. Все пустые множества считаются равными. Кроме того, вводится в рассмотрение одноэлементное множество, состоящее из единственного элемента. В результате абстракции множества одноэлементное множество оказывается не тем же самым предметом, каким является его элемент.
Интересно заметить, что еще в 1638 г. Г. Галилей обнаружил, что можно установить взаимно однозначное соответствие между натуральными числами и их квадратами, если выписывать одну под другой две строки (одновременно), включая в первую натуральные числа и тут же под ними во второй записывая квадраты этих чисел. Получается
0 1 2 3 4 5 6 7 8...
0 1 4 9 16 25 36 49 64...
Г. Галилей расценил это как парадокс, демонстрирующий нам, что квадратов «столько же», сколько и натуральных чисел, в то время как квадратов «гораздо меньше», чем всех натуральных чисел. Г. Кантор усмотрел в примере Г. Галилея равномощность множества натуральных чисел и множества их квадратов.
Из того факта, что все квадраты являются натуральными числами, но не все натуральные числа являются квадратами, следует, что множество квадратов является правильной частью [12] множества натуральных чисел. Если N означает множество натуральных чисел, a Q — множество их квадратов, то можно записать Q  N, что значит: q - правильная часть множества N. Заметим, что ни один элемент множества не считается его частью, так что знаки
N, что значит: q - правильная часть множества N. Заметим, что ни один элемент множества не считается его частью, так что знаки  и
и  имеют совершенно разный смысл.
имеют совершенно разный смысл.
Из примера Г. Галилея Г. Кантор сделал вывод, что некоторые множества могут быть равномощны своим правильным частям. Ни одно конечное множество не обладает таким свойством. Оно присуще только бесконечным множествам.
Натуральный ряд в теории множеств принят за эталон некоторого класса бесконечных множеств. Любое множество, равномощное натуральному ряду, называется счетным.
Итак, мы знаем уже конечные множества и счетные множества. Есть ли еще какие-нибудь? Оказывается, есть. Рассмотрим множество всех действительных чисел, каждое из которых больше нуля, но меньше единицы. С помощью специального приема, изобретенного Г. Кантором, можно доказать, что множество действительных чисел несчетно. Предположим противное, т. е. что мы сумели установить взаимно однозначное соответствие между действительными числами и натуральными числами. Говорят, что нам удалось действительные числа перенумеровать. Запишем эти числа в столбец в порядке номеров. Как известно, каждое действительное число из нашего множества имеет конечное либо бесконечное множество знаков после запятой. Можно считать, что количество знаков после запятой в записи каждого действительного числа бесконечно, так как в противном случае мы могли бы справа приписать сколько угодно нулей.
Предположим, что у нас получится следующий столбец действительных чисел:
0,5010203…
0,1020705…
0,0216973…
0,2329793…
0,2332750…
Составим еще одно число (назовем его b), у которого целая часть равна нулю, а i -я (i =1, 2,...) цифра после запятой либо на единицу больше i-й цифры после запятой i-ro действительного числа, либо, если это невозможно (потому что при сложении получается 10), равна нулю.
Другими словами, каждая цифра числа b получается из цифры, стоящей на диагонали нашей «таблицы цифр», увеличением на 1 (с отниманием 10, если получится двузначный результат). В нашем конкретном случае мы получим бесконечную строку цифр 0,61208...
Такая строка является записью действительного числа. Это число не равно ни одному из перенумерованных нами действительных чисел, так как его первая цифра после запятой не равна первой цифре после запятой первого числа, его вторая цифра не равна второй цифре второго числа и т. д. От каждого действительного числа это число заведомо отличается хотя бы одной цифрой.
Мы вели рассуждения исходя из условия, что все действительные числа нашего множества перенумерованы и в порядке номеров расположены в столбец. Но в результате этих рассуждений мы получили действительное число Ь, принадлежащее нашему множеству и не равное ни одному из перенумерованных (т. е. не имеющее номера). Мы пришли к противоречию. Остается сделать только один вывод: неверно, что наше множество действительных чисел счетно, оно несчетно.
Множества, равно мощные множеству действительных положительных чисел, не превосходящих единицы, называют множествами мощности континуума, или континуальными.
Кардинальные числа
Теория множеств позволяет сделать очень интересное обобщение понятия числа. Условимся мощностью конечного множества называть наибольшее натуральное число, которое будет использовано при нумерации его элементов, т. е. при установлении взаимно однозначного соответствия с последовательными числами 1, 2, 3,..., принадлежащими натуральному ряду. При этом мощности равномощных конечных множеств оказываются равными, что подтверждает естественность нового термина.
Множеству всех натуральных чисел поставим в соответствие некоторую мощность, которую будем обозначать символом N. Ее же будем считать мощностью каждого множества, равномощного множеству натуральных чисел (т. е. каждому счетному множеству). Будем, наконец, считать, что множеству положительных действительных чисел, не превосходящих единицы, соответствует некоторая мощность К, которая является мощностью также каждого континуального множества.
Если каждое множество, являющееся правильной частью множества М, а также само множество М называть подмножествами множества М, можно доказать теорему:
Если М — конечное множество мощности п, то множество всех его подмножеств (считаемых элементами этого нового множества) имеет мощность 2n (имеются в виду только попарно неравные между собой подмножества).
Мы не будем приводить доказательства этой теоремы, подтвердим ее только примером. Пусть множество М состоит из элементов а1, а2, а3 и, следовательно, имеет мощность 3. Его подмножествами будут три одноэлементных множества { a 1}, { a 2}, { а3 }, три двухэлементных множества { а 1, а 2}, { а 1, а 3}, { a 2, а3 }, одно трехэлементное множество { а1, а 2, а 3} и одно пустое множество { }. Их ровно восемь, а это значит, что мощность множества, для которого они являются элементами, равна 23.
Обратим внимание на способ обозначения множеств, которым мы пользовались. Мы перечисляли элементы множества и заключали их в фигурные скобки. Множество подмножеств множества М можно было обозначить так:
{{ }, { а1 }, { a 2, { a 3}, { a 1. a 2}, { a 1, а3 }, { а 2, а 3}, { a 1, а 2, а 3}}. По аналогии с мощностями конечных множеств условимся мощность множества всех (не равных между собой) подмножеств бесконечного множества обозначать символом 2т, если мощность исходного множества т. Доказано, что K=2N. При этом 2К будет равно  .
.
Мы не знаем, все ли возможные мощности могут быть обозначены с помощью введенных обозначений, но это пока для нас и неважно. Будем только считать, что для каждого множества (а значит, и для всех равномощных ему множеств) существует некоторая мощность.
Остается «установить порядок» между мощностями. Делается это так. Полагают, что мощности равиомощных множеств равны. Это условие уже выполнено. Далее, считают, что мощность множества M1 (обозначим ее m1) меньше мощности множества М2 (обозначим ее m2), если M1 равномощно некоторому подмножеству множества М2, причем М 2не равномощно ни одному подмножеству множества M1. Это записывают так:
m1<m2.
Наконец считают, что mt больше тг и пишут т1>тг, если сформулированное выше условие при взаимной замене M1на M2 окажется верным. Итак, теперь каждое множество характеризуется своей мощностью, и любые две мощности находятся в одном из трех перечисленных отношений.
Новая характеристика множества — его мощность — чем-то напоминает число, а для конечных множеств совпадает с числом. Это позволило ввести термин кардинальное число.
Кардинальным числом (элементов) множества М называется его мощность т. Все натуральные числа содержатся среди кардинальных, но существуют кардинальные числа, не являющиеся натуральными. Г. Кантор доказал следующие две теоремы.
Теорема 1. Для любого кардинального числа т справедливо неравенство m<2m.
Теорема 2. Мощность т' подмножества множества, имеющего мощность т, удовлетворяет неравенству т' ≤ т.
Теперь мы достаточно углубились в теорию множеств для того, чтобы суметь описать те «подземные толчки», которые потрясли математику в конце XIX — начале XX в.
Антиномии
В то время, когда А. Пуанкаре провозгласил, что математика обрела, наконец, надежный фундамент, сама арифметика пошатнулась из-за того, что в теории множеств были обнаружены противоречия (парадоксы), вошедшие в историю математики под названием антиномий.
Парадокс Кантора (обнаружен в 1899 г.). Пусть М — множество всех множеств. Обозначим его кардинальное число буквой т. В силу теоремы 1 кардинальное число множества его подмножеств 2т удовлетворяет условию 2m>m.
С другой стороны, множество М есть множество всех множеств. Его подмножества являются множествами и, значит, являются элементами М, а их множество, следовательно, является подмножеством множества М. Тогда в силу теоремы 2 должно иметь место неравенство 2т ≤ т.
Полученные два неравенства противоречат друг другу. В этом и проявляется парадокс (антиномия) Кантора.
Для создания парадоксальной ситуации мы привлекли к рассмотрению очень своеобразное множество всех множеств. Для него характерно то, что оно является своим собственным элементом, т. е. обладает свойством М  М. Возникает законное сомнение — а возможно ли это? Может быть, таких множеств не бывает? Оказывается, бывают и даже среди не очень сложных. Множество коров не может быть своим собственным элементом, потому что оно не корова. Но рассмотрим следующие два примера.
М. Возникает законное сомнение — а возможно ли это? Может быть, таких множеств не бывает? Оказывается, бывают и даже среди не очень сложных. Множество коров не может быть своим собственным элементом, потому что оно не корова. Но рассмотрим следующие два примера.
1. Известно, что акционерами могут быть любые юридические лица, юридическими же лицами являются отдельные граждане и акционерные общества. Если некое акционерное общество X скупило часть собственных акций, то X является как множеством акционеров, так и собственным акционером, т. е. удовлетворяет условию Х£Х. Ничего противоречивого или невозможного в этом нет.
2. Для построения еще одного примера представим себе, что у нас есть библиотека, и в ней мы решили создать разделы (т. е. выделить множества книг). Для этого будем для каждого раздела составлять каталог и оформлять его в виде книги. Каждый каталог определяет некоторое множество книг. Очевидно, каталог может содержать в себе данные о самом себе. Такой каталог будем называть самоназывающимся, а каждый каталог, который не содержит сведений о самом себе, несамоназывающимся. Любой самоназывающийся каталог, с одной стороны, является книгой, а с другой — определяет множество книг (при абстрактном подходе говорят — является множеством книг), в которое сам входит.
Существование множеств, содержащих самих себя в качестве элементов, еще не парадоксально. Но вместе с некоторыми другими условиями оно может приводить к возникновению парадокса.
Кардинальное число является некоторой количественной характеристикой множества. Введем и мы такую характеристику для книг и каталогов.
Каждая книга в нашей библиотеке имеет цену, проставленную на ее переплете. Будем эту цену считать количественной характеристикой книги. Установим правило, согласно которому оценка каталога производится так: определяется максимальная цена книги из числа указанных в каталоге и прибавляется к этой величине 1 рубль. Это и будет цена каталога. Если обозначить цены указанных в каталоге книг через y1, y2, …, yi, …, yn,а цену каталога через х, то можно написать формулу для оценки каталога:
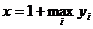 .
.
Теперь нам легко создать парадоксальную ситуацию.
Парадокс оценки каталогов. Директор библиотеки, узнав о большом числе каталогов в его библиотеке, принял решение создать раздел всех каталогов. Новый каталог был довольно быстро составлен, а вот с определением его цены произошла заминка. Для определения этой цены каталогизатор поступил так: если
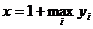
то при любом i имеем x≥1+yi. Но одна из книг, указанных в каталоге, есть сам этот каталог; значит, его цена может быть подставлена в последнюю формулу, что даст неравенство х^1+х.
Найти такую цену х, которая удовлетворяла бы последнему условию, каталогизатор никак не мог. Тогда директор сказал: «Очевидно, каталог всех каталогов такая дорогая вещь, что оценить его невозможно. Давайте ликвидируем в библиотеке раздел каталогов, а каждый каталог включим в тот раздел, который в нем описан». К удивлению директора, после этого сразу все каталоги перестали поддаваться оценке.
Как директор разрешил парадокс оценки каталогов? Очень просто. Не математическими, а административными средствами. Он предложил вместо правила
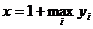
применить правило
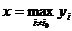
(i0 — номер каталога в нем самом).
Каталогизатор стал возражать, мотивируя тем, что за составление каталога ему положена плата, равная цене, проставляемой на каталоге. Предлагаемое директором изменение способа оценки каталогов уменьшит его заработок на столько рублей, сколько он составит каталогов. Но директор не смутился. Он издал приказ, по которому для каталогов была установлена новая оценка
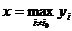
но за каждый составленный каталог составителю полагается премия в сумме 1 рубль, после чего цена каталога должна быть увеличена на 1 рубль.
Мы привели здесь новое правило оценки каталогов для того, чтобы показать, что парадокс возникает только При определенных способах приписывания множествам числовых характеристик.
Парадокс Рассела (открыт в 1902 г.). Если парадокс Кантора возникает для множества, которое содержит себя в качестве своего элемента, то парадокс Рассела связан с множествами, не содержащими себя в качестве своих элементов. Для удобства будем множество, не содержащее себя в качестве элемента, называть обычным, а множество, содержащее себя в качестве элемента,— необычным.
Парадоксальным является множество всех обычных и только обычных множеств. Чтобы в этом убедиться, проверим, является ли оно само обычным или необычным. Сперва предположим, что оно обычное. Но тогда, будучи множеством всех обычных множеств, оно содержит и себя. Стало быть, оно необычное. Предположив, что оно обычное, мы получили противоречие.
Но, может быть, оно необычное, и дело с концом? Проверим. Если оно необычное, то, будучи множеством только обычных, оно себя в качестве элемента не содержит, а значит, является обычным. Опять противоречие.
Интересно, что парадокс Рассела может возникнуть и для каталогов, которыми мы уже пользовались для построения парадокса Кантора.
Парадоксальным оказывается каталог всех несамоназывающихся и только несамоназывающихся каталогов. Он не может быть самоназывающимся (содержать сведения о самом себе), так как является каталогом только несамоназывающихся каталогов. Точно так же он не может быть и несамоназывающимся, так как при этом не содержал бы сведений о себе (несамоназывающемся), но должен был бы содержать.
Парадокс брадобрея. Парадокс Рассела можно сформулировать без привлечения понятия множества. Представим себе, что один из солдат оказался по профессии парикмахером. Узнав об этом, командир полка приказал ему брить всех тех и только тех, кто сам себя не бреет. Все было хорошо, пока не пришло время побрить самого себя. Оказалось, что побрить себя нельзя, так как приказано брить только тех, кто себя не бреет; не брить себя тоже нельзя, потому что приказано брить всех, кто себя не бреет.
Не кажется ли читателю, что положение брадобрея подобно положению юноши, решившего купить костюм, цена которого меньше 50 рублей (потому что это дешевый костюм) и больше 150 рублей (потому что это хороший костюм)? Разница лишь в том, что условия для покупки костюма всегда противоречивы (не зависят от объекта покупки), а условия, при которых следует брить, не всегда: их противоречивость или непротиворечивость зависит от объекта бритья.
Выводы из антиномий
Открытие антиномий потрясло математику и математиков как землетрясение. Их наличие, и при этом в такой области, как теория множеств (и логика, потому что парадокс брадобрея имеет логический характер), заставило опасаться того, что многие результаты, полученные в математике, тоже противоречивы. Можно было ожидать, что в дальнейшем будут появляться еще новые парадоксы. Все в математике стало казаться неустойчивым, потому что самый ее фундамент дал трещину.
Нужно сказать, что математики реагировали на землетрясение по-разному. Одни стали во всем сомневаться. Известный математик Ю. Дедекинд после опубликования антиномии Рассела на некоторое время прекратил публикацию своих работ. Математик Г. Фреге кончал в это время издание своего большого труда, подготовке которого он посвятил десять лет жизни. В первой же фразе послесловия он говорит, что фундамент построенного им здания поколеблен парадоксом Рассела. А. Пуанкаре, о котором мы уже говорили, изменил свое отношение к теории множеств. Были, конечно, и такие математики, которые на открытие антиномий никак не реагировали и бездумно продолжали применять теорию множеств, правда, в той ее части, в которой не обнаружено антиномий. Этих математиков обычно называют последователями классицизма. Но многие математики стали искать пути устранения противоречий.
Некоторые полагали, что противоречия возникают благодаря дефектам самой логики и стали пересматривать именно ее.
Другие предполагали, что парадоксы возникают из-за некорректности понятия множества, и занялись поиском такого определения множества, которое было бы свободно от внутренних противоречий.
Третьи — получившие название формалистов — пришли к выводу, что математика должна быть аксиоматизирована, а затем все теоремы совершенно формально доказаны. При этом возник вопрос о формальном языке для математики, таком, чтобы с аксиомами, изложенными на нем, можно было поступать как с определенными комбинациями символов. Доказательство теорем при этом принимало вид переработки исходных аксиом с помощью правил вывода в новые комбинации символов — теоремы. Эти математики разработали новую дисциплину — теорию математического вывода, называемую метаматематикой.
Четвертые усмотрели причину кризиса математики в том, что ряд математических объектов и методов являются неконструктивными. Разъясним последнюю точку зрения.
В теории множеств допускаются «готовые» бесконечные множества, уже существующие, уже завершенные. Завершенное бесконечное множество называют актуально бесконечным. Расходуя ограниченное количество ресурсов на каждом шаге, имеющем фиксированную длительность, построить такое множество ни реально, ни потенциально нельзя. Проверить, обладают ли все элементы такого множества каким-либо свойством, тоже нельзя, так как никакая ограниченная скорость проверки не дает возможности охватить их все. Другое дело, потенциально бесконечное, или потенциально осуществимое множество. Такое множество в каждый момент конечно, но есть прием, позволяющий добавить к нему всегда еще несколько (а потом еще несколько, и еще несколько, и так далее и, значит, сколько угодно) элементов. Анализ элементов такого множества можно провести исследованием правила, которое позволяет получать все новые и новые элементы этого «конструктивного» множества.
Актуально бесконечное множество, будучи недоступно ни построению, ни проверке, обязывает нас слепо доверять тем правилам логики, с помощью которых мы определили свойства его элементов. Указанные правила логики не основываются ни на каких фактах, доступных проверке, во всяком случае в смысле их правильности для актуально бесконечных множеств. Значит, говорят математики, придерживающиеся этой четвертой точки зрения, всей части теории множеств, имеющей деле с актуальной бесконечностью, доверять нельзя.
Будучи едины в своем отношении к актуальной бесконечности и в своем требовании конструктивности, сторонники четвертой точки зрения неодинаково решают вопрос о том, что допустимо в качестве исходного материала для конструкций. Таким образом, эта точка зрения делится на две группы.
Математики первой группы считают, что главным основанием для выбора какого-либо математического объекта в качестве исходного для дальнейших построений является его интуитивная очевидность. Читатель, вероятно, согласится, что выбор, опирающийся на интуицию, не может не быть субъективным. То, что интуитивно ясно одному, совершенно неясно другому. Это течение в математике получило название интуиционизма.
Математики второй группы считают, что исходным материалом для построений могут быть лишь наиболее простые математические объекты, применение которых оправдано всей практикой человечества, причем количество их типов должно быть ограничено. В качестве основного средства получения новых математических объектов должны служить алгоритмы. Это направление получило название конструктивного.
Нужно признать, что ученые всех перечисленных направлений внесли большой вклад в сокровищницу математики, получили большое число очень интересных, глубоких и важных научных результатов. Нужно также подчеркнуть, что наше описание различных точек зрения, возникающих в результате обнаружения антиномий, является упрощенным и неточным. Но более подробно осветить этот вопрос автор не имеет возможности.
Из всех указанных направлений мы выделим последнее — конструктивное, поскольку оно для обоснования математики приняло на вооружение алгоритмы, и его сторонники стали разрабатывать теорию алгоритмов.
Итак, мы ознакомились со второй причиной для разработки теории алгоритмов: необходимостью обоснования математики.
На этом автор хотел закончить главу, но вдруг понял, что любознательный читатель, узнав о том, что произошло в математическом мире в начале XX в., несомненно захочет узнать — а как же дело обстоит сейчас? Рассыпалась ли математика, как карточный домик, или она устояла, преодолела свой кризис?
Конечно, появление антиномий потрясло математику. Верно и то, что кризис математики еще и до сих пор полностью не преодолен. Три четверти столетия — слишком малый для этого срок.
Но в общем-то оснований для отчаяни




 . Запись а
. Запись а  N, что значит: q - правильная часть множества N. Заметим, что ни один элемент множества не считается его частью, так что знаки
N, что значит: q - правильная часть множества N. Заметим, что ни один элемент множества не считается его частью, так что знаки  .
.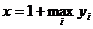 .
.