Сосуды высокого давления (толстостенные). Причины разделения сосудов на тонко и толстостенные. Напряжения, возникающие в толстостенной цилиндрической оболочке под действием внутреннего избыточного давления, построение эпюр напряжений. Анализ формул и эпюр.
К аппаратам высокого давления (толстостенные) относят аппараты, работающие под давлением свыше 10 МПа. Толщина стенки корпуса такого аппарата превышает 10% его внутреннего диаметра, т.е. коэффициент толстостенности (отношение наружного диаметра к внутреннему) β = Dн/D>1,2. Обычно аппараты высокого давления изготавливают по возможности меньшего диаметра, что позволяет получить относительно небольшое усилие от внутреннего давления на крышку аппарата и тем самым обеспечить конструктивное совершенство ее элементов уплотнения. Наиболее употребительные отношения диаметра корпуса к его высоте D/H: 1:10 и 1:15. Толщина стенки толстостенных сосудов может достигать 600 мм при D = 1м.
Корпуса аппаратов в зависимости от способа их изготовления бывают литые, кованые, сварные и многослойные.
Для толстостенных оболочек нельзя применять распределение σt по толщине стенки равномерным и пренебрегать радиальным напряжением, т.к. давление может достигать порядка 600 МПа и тогда σr = 600 МПа (на внутренних волокнах), что значительно больше допускаемых напряжений и соизмеримо с σt. В этом случ. напряж. сост. материала оболочек – объёмное (трехосное).
Основные причины, по которым аппараты подраздел.на тонко- и толстостенные:
2. отличие напряжённых состояний материала оболочек:
– для тонкостенных – двухосное (σr ≈0; σm≠0; σt≠0);
– для толстостенных – объёмное (σr ≠0; σm≠0; σt≠0);
2. различный характер распределения тангенциальных напряжений но толщине стенки:
- для тонкостенных - равномерное;
- для толстостенных - неравномерное.
Основными признаками деления сосудов на тонко- и толстостенные являются соотношение толщины стенки S к внутреннему диаметру Dв значение давлений, Т.е.
- для тонкостенных
а) S-C/ Dв ≤0,1 (при Dв> 200 мм) или β = Dн/ Dв<1,2, где β - коэф. толстостенности;
 б) Р≤10 МПа (условное разделение)
б) Р≤10 МПа (условное разделение)
- для толстостенных
а) S-C/ Dв>0,1; β>1,2;
б) Р>10 МПа
Цель расчета толстостенных аппаратов заключается в получении формул для нахождения напряжений σr; σm; σt. В цил.обечайке без днищ возникают радиаль. и тангенц. Напряжения:

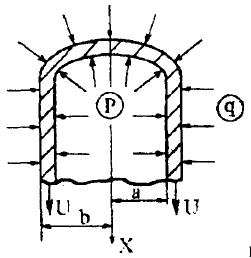 Здесь r – текущий радиус, т.е. значение, при котором необходимо рассчитать напряжение. Величина r может выбираться в пределах от r = a до r = b. Если цилиндрическая обечайка имеет днища, то при действии на них внутреннего и наружного давлений возникает меридиональная сила U и соответственно меридиональное напряжение σm.
Здесь r – текущий радиус, т.е. значение, при котором необходимо рассчитать напряжение. Величина r может выбираться в пределах от r = a до r = b. Если цилиндрическая обечайка имеет днища, то при действии на них внутреннего и наружного давлений возникает меридиональная сила U и соответственно меридиональное напряжение σm.

Обычно q = 0, тогда уравнения упрощаются:
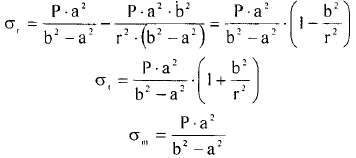
Сравнивая σm с суммой напряжений (σt+ σr), получим зависимость, связывающую все 3 напряжения между собой, т.е.
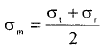
Рассмотрим распределение напряжений по толщине стенки в сечении, например 1-1. Для этого проанализируем формулы
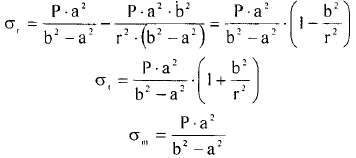
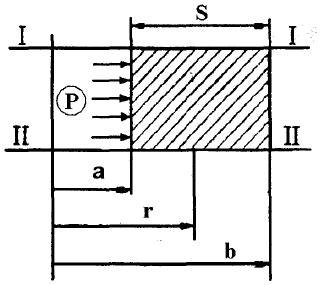 Как видно, σr, σt для какого то конкретного аппарата (при заданных a,b,P) зависит от текущего радиуса, т.е.
Как видно, σr, σt для какого то конкретного аппарата (при заданных a,b,P) зависит от текущего радиуса, т.е.

А σm – постоянно по толщине стенки.
Сопоставим между собой σr и σt. Для этого определим эти напряжения при r=a и r=b:
а) r=a

Т.к. (b2+a2)>(b2-a2), то при r=a σt>0 и | σtа|>| σrа|, а меридиональное напряжение равно

Так как для толстостенных аппаратов 
Где β – коэффициент толстостенности, то, например при β=1,5, значение меридионального напряжение при r=a составит
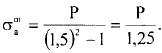
Таким образом, анализ напряжений, действующих на внутр. Волокнах, показывает, что

б) r=b,

Чтобы определить на сколько отличаются тангенциальные напряжения при r=b и r=a найдём величину σtа - σtb:
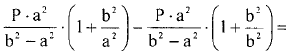


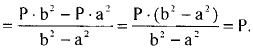
Таким образом, σtа - σtb = Р.
Сравнение т.ж. показывает, что σtb> σmb. Строим эпюры

Таким образом, анализ изменения этих напряжений по толщине стенки показывает, что по абсолютному значению σt и σr максимальны на внутренних волокнах, σm – постоянны по S. При давлении Р, не изменяющемся вдоль меридиана (равномерном газовом давлении), эпюры напряжений одинаковы по высоте аппарата.
Анализ распределения напряжений по толщине стенки показывает, что наиболее опасные – внутренние волокна. Для них условие прочности по 3 теории прочности может быть записано след.образом:
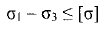
Т.к. σtа> σmа> σrа, то σ1= σt, σ2 = σm, σ3 = σr, тогда условие прочности перепишется в виде
σt - σr ≤ [σ] при r = a
При r = а напряжения σt и σr соответственно равны

Подставив эти значения в условие прочности, получим



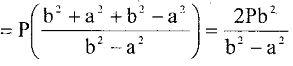 .
.
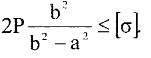
Заменив в последней формуле b на Dн/2 и а на Dв/2, получим

Произведя ряд преобразований:

Получим уравнение для расчёта толщины стенки толстостенного аппарата:


9. Толщина стенки однослойного (монолитного) цилиндрического сосуда, находящегося под воздействием внутреннего избыточного давления (без вывода). Анализ формулы. Методы повышения несущей способности однослойных сосудов. Условие оптимальности. Толщина стенки многослойных сосудов.


Для толстостенных сосудов давление P достигает больших значений, соизмеримых с допускаемыми напряжениями, и при значениях 2P> 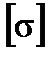 , уравнение не имеет решения. Необходимо повысить несущую способность одним из нижеприведенных способов.
, уравнение не имеет решения. Необходимо повысить несущую способность одним из нижеприведенных способов.
Многослойные цилиндры создаются путем надевания одного цилиндра на другой в горячем состоянии, с натягом. Каждый последующий цилиндр имеет внутренний радиус несколько меньше внешнего радиуса цилиндра, на который он одет. Разница между обоими радиусами составляет натяг. Охлаждаясь, внешний цилиндр, надетый на внутренний с натягом в горячем состоянии, сжимает внутренний цилиндр. На поверхности раздела двух цилиндров возникает так называемое монтажное давление - Рм, под действием которого внутренний цилиндр сжимается, а внешний - растягивается, т.е. оболочка 1 нагружена наруж. давлением, а 2-внутренним.
Анализ формул и эпюр распределения напряжений по толщине стенки толстостенного аппарата показывает что: наиболее нагружены внутренние волокна, т.к  и
и  имеют максимальные значения; напряжения по мере удаления от внутренней поверхности снижаются весьма быстро.
имеют максимальные значения; напряжения по мере удаления от внутренней поверхности снижаются весьма быстро.
Увеличить несущую способность это значит сконструировать таким образом чтобы при меньшей толщине стенки аппарат мог воспринимать большую нагрузку (давление). Это может быть достигнуто путем: а) уменьшения напряжений на внутренних волокнах; и б) более равномерного распределения их по толщине стенки. Методы увеличения несущей способности: 1) создание многослойных сосудов; 2) метод автофреттирования (автокрепления, самокрепления).
Автофреттирование – использование остаточных деформаций для повышения прочности однослойных сосудов.
При повышении внутреннего давления однослойного цилиндра напряжения возврастают. Если напряжения на внутренних слоях будут превосходить предел текучести материал начнет течь. А слои где напряжения ниже предела текучести останутся упругими. Если не доводя до разрыва будем уменьшать давление, та часть стенки которая пришла в пластическое состояние будет иметь остаточные деформации и ее радиус будет стремиться оставаться несколько больше первоначального. Наружные слои будут стремиться вернуться в первоначальное состояние (т.к упругие), но им будут препятствовать внутренние слои. Поэтому внешние слои останутся, немного растянутыми, т. е наблюдается картина надевания сосудов друг на друга с натягом и создании монтажного давления. Если после этого нагрузить сосуд рабочим давлением напряжения, возникающие от него будут складываться алгебраически с напряжениями, возникающими при автофреттаже. В результате более равномерное распределение напряжений.
Сосуд считается спроектированным оптимально, если эквивалентные напряжения на внутренних радиусах каждого цилиндра равны между собой, т.е. равномерное распределение напряжений по толщине стенки. Для двухслойного сосуда условие оптимальности:  . Гадолин определил:
. Гадолин определил:  с-радиус сопряжения; а- внутренний радиус, b- наружный радиус.
с-радиус сопряжения; а- внутренний радиус, b- наружный радиус.

Соотношение Гадолина справедливо если двухслойный цилиндр изготовлен из одного материала.
Если слоев больше то условие Гадолина примет вид:  n-число слоев,
n-число слоев,  - радиус сопряжения i-го слоя.
- радиус сопряжения i-го слоя.
Толщина стенки по 3 теории прочности: 
По 4: 
Для двухслойных сосудов при расчете напряжений может применятся метод, согласно которому отдельно определяются напряжения от внутреннего давления для монососуда и от монтажного давления для двухслойного, а затем путем суммирования эпюр, находятся напряжения в составном сосуде.при числе слоев более 2 этот метод применять трудно и напряжения могут быть найдены по методу начальных параметров.
 - для многослойного (n-число слоев).
- для многослойного (n-число слоев).
10. Механические колебания валов. Критическая скорость вала с одним грузом (анализ формулы динамического прогиба). Условие виброустойчивости. Явление самоцентрирования.
Колебаниями (колебательным движением) называют все виды движения (или изменения состояния), которые обладают какой-либо степенью повторяемости во времени. Колебания наз-ся периодическими, если значения величин, изменяющиеся в процессе колебаний, повторяются через равные промежутки времени. Колебания характеризуются несколькими параметрами, среди которых: период, частота, циклическая (круговая) частота.
Различают колебания:
- материальных объектов, все три измерения которых сравнимы между собой (фундаменты машин);
- оболочек (тонкостенных цилиндров, сфер) и тонкостенных пластин, т.е. тел, два измерения которых значительны по сравнению с третьим (толщиной);
- стержней, т.е. тел, в которых одно измерение (длина) весьма велико по сравнению с двумя другими. Валы относятся к стержням.
Различают 3 типа колебания стержней:
1) продольные колебания – сечения стержней колеблются вдоль оси стержня около положения равновесия;
2) поперечные колебания или колебания изгиба – сечения стержня смещаются нормально к его оси поочередно по одну и другую сторону от положения равновесия, поворачиваясь при этом вокруг своих нейтральных осей;
3) крутильные колебания – сечения стержня поворачиваются на некоторый угол φ, оставаясь в своей плоскости, вокруг оси стержня попеременно в одну и другую стороны.
Валы машин обычно совершают поперечные колебания.
Величина динамического прогиба:
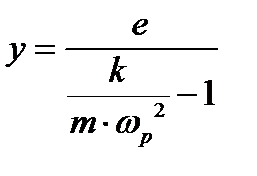
где  - рабочая угловая скорость вращения вала;
- рабочая угловая скорость вращения вала;
k – коэффициент жесткости вала, то есть сила, вызывающая прогиб, равный единице.
Угловая скорость собственных (свободных) колебаний невесомого вала с одной сосредоточенной массой:
 Тогда:
Тогда: 
Угловая скорость колебаний вала, при которой прогибы значительно возрастают и вращающиеся валы становятся динамически неустойчивыми, наз-ся критической ωкр.
Из уравнения видно, что для вала с одним диском ωкр равна угловой скорости свободных колебаний: 
Эту формулу обычно приводят к более удобному для расчета виду:
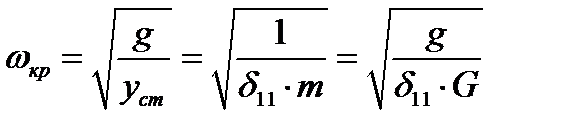
где  - единичный прогиб или коэффициент влияния, то есть Yст от единичной поперечной силы;
- единичный прогиб или коэффициент влияния, то есть Yст от единичной поперечной силы;
g – ускорение свободного падения;
Ycт- статический прогиб вала под массой m=G/g
Следовательно, вращение вала с рабочей скоростью, равной критической или близкой к ней, недопустимо. Рабочая скорость должна быть либо больше (для гибких валов), либо меньше (для жестких валов) критической угловой скорости.
Рекомендуется принимать:
- для жестких валов: ωр  0,7ωкр
0,7ωкр
- для гибких валов: ωр>1,3ωкр
Метод Донкерли
В методе Донкерли используется принцип независимости воздействия отдельных масс на колебания вала (принцип суперпозиции). Формула Донкерли, по которой определяется наименьшее возможное значение основной частоты  , может быть представлена в следующем виде:
, может быть представлена в следующем виде:
 , (9)
, (9)
где  – критическая угловая скорость вала, когда он нагружен только одним грузом массой mi;
– критическая угловая скорость вала, когда он нагружен только одним грузом массой mi;
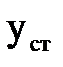 – статический прогиб вала под массой mi, когда он нагружен только этой массой (рисунок 11);
– статический прогиб вала под массой mi, когда он нагружен только этой массой (рисунок 11);
i – число масс на валу.
 Метод Донкерли дает заниженное значение
Метод Донкерли дает заниженное значение  . Однако во многих случаях практики достаточно констатировать, что критическая частота вала не ниже определенного предела, чтобы сделать излишним более точное решение.
. Однако во многих случаях практики достаточно констатировать, что критическая частота вала не ниже определенного предела, чтобы сделать излишним более точное решение.

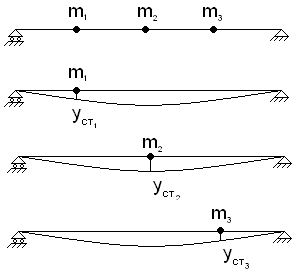
Рисунок 11 – Расчетная схема и первая (низшая) критическая скорость вала, нагруженного тремя сосредоточенными массами, определяемая по методу Донкерли.
по таблице для однопролетного и консольного валов на неподатливых подшипниках представлены значения коэффициентов  , подстановка которых в формулу (10) позволит определить
, подстановка которых в формулу (10) позволит определить  , а, следовательно, и проверить условие виброустойчивости (8).
, а, следовательно, и проверить условие виброустойчивости (8).
Энергетический метод Релея
В основе энергетического метода лежит принцип постоянства энергии, согласно которому максимальная потенциальная энергия деформации при вращении вала  равна максимальной кинетической энергии системы
равна максимальной кинетической энергии системы  , то есть
, то есть  .
.
После раскрытия данного равенства получено одно из выражений для расчета нижней критической частоты
 , (11)
, (11)
где  – статический прогиб вала под грузом массой
– статический прогиб вала под грузом массой 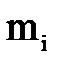 , нагруженного всеми нагрузками (рисунок 12).
, нагруженного всеми нагрузками (рисунок 12).

 (12)
(12)
Рисунок 12- Расчетная схема и первая (низшая) критическая скорость вала, нагруженного тремя сосредоточенными массами (метод Релея).
Критическая частота, получаемая по методу Релея, всегда выше действительной частоты (т.е частоты, найденной точным методом).. Действительная частота находится между частотой, определенной по формуле Донкерли  и частотой, найденной по методу Релея
и частотой, найденной по методу Релея  , то есть:
, то есть:
 . (13)
. (13)
Рассмотренные выше методы определения первой критической скорости вращения валов, в которых прогибы рассчитываются аналитически, просты и удобны в случае валов постоянного сечения и с небольшим числом нагрузок.
При расчете балок переменного сечения со многими сосредоточенными массами  может быть определена этими же методами, то есть по формулам (11) и (12), но в которых прогибы находятся графо-аналитически.
может быть определена этими же методами, то есть по формулам (11) и (12), но в которых прогибы находятся графо-аналитически.
Методы в этом случае называются графо-аналитическими.
В литературе приводится еще ряд методов для расчета валов переменного сечения. В практике химического машиностроения получил распространение так называемый метод приведения, основанный на исследованиях академика Ю. А. Шиманского /4/, который является достаточно простым, точным и универсальным, так как может быть применен как при расчете валов переменного, так и постоянного сечения, с одной или несколькими сосредоточенными массами, с учетом или без учета массы вала.
Критерии устойчивости.



Неустойчива Устойчива Безразличное состояние
Определяем положение интуитивно.
В некоторых случаях интуитивно определить сложно


Неизвестно.
- энергетические
Под действием нагрузки определяется приращение потенциальной энергии 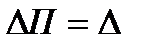 V+
V+  Т
Т
 Т-работа внешних сил,
Т-работа внешних сил,  V-приращение внутренней энергии. Если
V-приращение внутренней энергии. Если  П>0, т. е.
П>0, т. е.  V>
V>  Т
Т
то система устойчива; если  П<0, т. е.
П<0, т. е.  V<
V<  Т, не устойчив.
Т, не устойчив.
Система считается неустойчивой если полная потенциальная энергия имеет минимум.
-Динамический
-Статический
По статическому критерию положение равновесия считается неустойчивой, если при воздействии нагрузки появляются новые бесконечно близкие к исходной форме равновесия.
Для стержня появляются новые и новые формы равновесия.

Когда система переходит из устойчивой в неустойчивое положение равновесие - это явление называется потеря устойчивости.
Потеря устойчивости сопровождается внезапным ростом деформации, прогибы сопровождаются резким качественным изменением первоначальной формы.
Система может терять устойчивость: а) чрезмерные деформации (трещены)
б) систему можно эксплуатировать
Нагрузка при которой система теряет устойчивость называется критической.
Цель расчета Определение Fkp, Рkp, Мkp;Определение допускаемых нагрузок по формулам:
[Pн]у=  ; [F]у=
; [F]у=  [М]у=
[М]у= 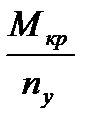 ;
;
Где Ркр, Fкр, Мкр – соответственно критическое давление, осевая сжимающая сила и изгибающий момент, МПа, Н, Н×м;
nу- коэффициент запаса устойчивости, который равен: для рабочих условий nу= 2,4; для условий испытаний и монтажа nу = 1,8
Потеря устойчивости цилиндрических оболочек от действия осевой сжимающей силы может быть общей или местной в зависимости от соотношения расчетной длины lp к внутреннему диаметру D.
а) При lp/D  10 оболочка рассматривается как длинный стержень, происходит общая потеря устойчивости.
10 оболочка рассматривается как длинный стержень, происходит общая потеря устойчивости.
Допускаемая и к ритическая осевая сжимающая сила из условия общей потери устойчивости определяются по формуле
[F]E2= 
 , (3.1)
, (3.1)
 -формула Эйлера
-формула Эйлера
где 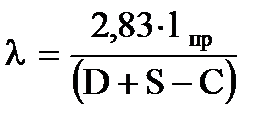 - гибкость оболочки;
- гибкость оболочки;
 Dcp=D+(S-C);
Dcp=D+(S-C); 
lпр - приведенная расчетная длина центрально сжатой оболочки, определяемая в зависимости от способа закрепления, м;
Для рассматриваемой в лабораторной работе схемы приведенная длина равна lпр = 2×l, где l –длина оболочки.
б) При lp/D< 10 происходит местная потеря устойчивости
Обычно потеря устойчивости в этом случае происходит внезапно, хлопком, с образованием глубоких ромбических вмятин, обращенных к центру кривизны согласно. Вдоль образующей располагаются несколько поясов вмятин. Такую форму потери устойчивости называют несимметричной. Реже наблюдается осесимметричная форма с образованием в окружном направлении одной кольцевой вмятины, как на рисунке (обычно это происходит при одновременном действии осевой сжимающей силы и внутреннего давления).
 Допускаемая и критическая осевая сжимающая сила из условия местной потери устойчивости определяется по формуле
Допускаемая и критическая осевая сжимающая сила из условия местной потери устойчивости определяется по формуле
[ F ]E1 =  ,
,
где Е- модуль упругости, МПа, для соответствующего расчетного условия ( ,
,  );
);
q nу– коэффициент запаса устойчивости.
Данный коэффициент имеет следующие значения: для рабочих условий nу = 2,4; для условий испытаний и монтажа nу = 1,8.
Затем определяется меньшее из двух, найденных по формулам значение допускаемой осевой сжимающей силы 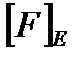 , т.е.
, т.е. 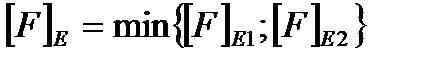 .
.
В случае, если  , формула принимает вид
, формула принимает вид
 .
.
Разрушение сжимающего элемента может быть следствием: потери устойчивости; потери прочности; потери того и другого.
В этом случае значение допускаемой осевой сжимающей силы определяется по формуле

где  - допускаемое осевое сжимающее усилие из условия прочности, Н, которое определяется по формуле:
- допускаемое осевое сжимающее усилие из условия прочности, Н, которое определяется по формуле:  .
.
Устойчивость цилиндрических оболочек. Причина потери устойчивости. Различные формы потери устойчивости под действием наружного давления. Понятие расчетного давления и расчетной длины. Формулы для расчета допускаемых нагрузок для каждой из этих форм.Область применения каждой формулы.
Тонкостенные оболочки под действием определенных нагрузок (например, наружного давления) могут потерять устойчивость, причем можно рассматривать потерю устойчивости положения и потерю устойчивости формы.
Основанная причина потери устойчивости формы?
Для ответа на этот вопрос рассмотрим колонный аппарат под действием равномерного давления.
 Для цилиндра:
Для цилиндра:
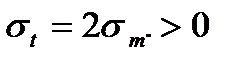
Растягивающие усилия:


Исходя из этого заключаем, что прочность обеспечена и существует большой запас напряжения.




Эквивалентные напряжения оказываются одинаковыми, если действуют внутренние и наружные давления равные по величине, то есть с точки зрения прочности 2 оболочки
Равнопрочные и имеют большой запас прочности.
В реальности часто оболочки хорошо спроектированы с точки зрения прочности и имеющие большой
запас разрушаются, эти оболочки, которые работают под действием наружного давления.
Отличие напряженного состояния для этих 2х оболочек состоит в том, что под действием внутреннего давления напряжения растягивающие, что способствует сохранению устойчивости, а с точки зрения наружного давления напряжения сжимающие, которые приводят к потери устойчивости формы оболочки причем потери устойчивости могут происходить внезапно, резко
происходит быстрый рост деформаций, например вмятины на оболочке и могут появляться
трещины, которые очень быстро растут и приводят к разрушению.
Сжимающие напряжения могут появляться так же под действием осевой сжимающей силы и от изгибающего момента, от поперечной нагрузки.
Причина потери устойчивости формы появления сжимающихся напряжений под действием:
 -наружного давления (вакуумная колонна, аппарат с рубашкой, трубопроводы под водой);
-наружного давления (вакуумная колонна, аппарат с рубашкой, трубопроводы под водой);
-осевая нагрузка;
-изгибающий момент.
Понятия устойчивости очень много, теории устойчивости до конца не сформулированы.
Устойчивость – это свойство системы сохранять свое состояние при внешних воздействиях.
Потеря устойчивости – резкое качественное изменение характера деформаций и первоначальной геометрической формы.
Существует понятие критической нагрузки (наименьшие) нагрузки при которой происходит потеря устойчивости формы.
Задачи теории устойчивости получить формулы по которой мы можем определить наименьшие критические нагрузки.
При одновременном действии всех трех нагрузок условие устойчивости согласно ГОСТ 14249-94 имеет вид
Pн.р./ [Pн] + F /[F] + М/[М] £ 1
При отсутствии одной или двух из нагрузок: наружного давления, осевой сжимающей силы или изгибающего момента в выражении (1.1) принимают соответственно Pн.р. = 0, F= 0 или М= 0.
Значения [F], [М], [Pн] определяются по формулам
[Pн] = 
 ,[F] =
,[F] =  [М] =
[М] =  ,
,
Значения допускаемых нагрузок из условия устойчивости, определяются по формулам
[Pн]у=  ; [F]у=
; [F]у=  ; [М]у=
; [М]у= 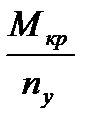
Критерии устойчивости.



Неустойчива Устойчива Безразличное состояние
Определяем положение интуитивно.
В случаях ниже мы не можем сказать положение устойчиво или нет, это зависит от соот-
ношения нагрузки, жесткости пружины и длины стержня.


Неизвестно.
В этом случае применяют критерии устойчивости:
- Энергетические
Под действием нагрузки определяется приращение потенциальной энергии 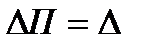 V+
V+  Т
Т
 Т-работа внешних сил,
Т-работа внешних сил,  V-приращение внутренней энергии. Если
V-приращение внутренней энергии. Если  П>0, т. е.
П>0, т. е.  V>
V>  Т
Т
то система устойчива; если  П<0, т. е.
П<0, т. е.  V<
V<  Т, не устойчив.
Т, не устойчив.
Система считается неустойчивой если полная потенциальная энергия имеет минимум.
-Динамический
-Статический
По статическому критерию положение равновесия считается неустойчивой, если при воздействии нагрузки появляются новые бесконечно близкие к исходной форме равновесия.
Для стержня появляются новые и новые формы равновесия.

Когда система переходит из устойчивой в неустойчивое положение равновесие - это явление называется потеря устойчивости.
Потеря устойчивости сопровождается внезапным ростом деформации, прогибы сопровождаются резким качественным изменением первоначальной формы.
Система может терять устойчивость: а) чрезмерные деформации (трещены)
б) систему можно эксплуатировать
Нагрузка при которой система теряет устойчивость называется критической.
1) Расчетное давление:
- для аппаратов с рубашкой:
 ;
;
-для вакуумных колонн:
 ;
;
В качестве наружного давления могут выступать: давление рубашек, подводная лодка, трубопроводы под водой, под грунтом.
2) Расчетная длинна

Расчетная длина для сосудов и аппаратов с выпуклыми днищами определяется следующим образом:
lp= lцилиндр+ lприлегающего элемента
lp= l + ho +  ,
,
где l - длина обечайки, находящейся под действием наружного давления, м;
h0 - высота цилиндрической части (отбортовки) днища, м;
Н – глубина днища, м.
Оболочки под действием наружного давления разделены на 2 типа, в зависимости от влияния условий закрепления по торцам на деформации от поперечного сечения оболочки.
Потеря устойчивости под действием наружного давления может происходить в зависимости от Lр – расчетной длины, L0 - длина разделяющая оболочки на длинные и короткие.
а) Lр/L0>0 длинная, б)- Lр/L0<0-короткая.
lo = 9,45×D×  ,
,
Для длинных оболочек условия закрепления мало влияют на деформации поперечного сечения, поэтому цилиндрические обечайки и трубы теряют устойчивость с образованием двух волн смятия (n=2) рис.а
Короткие цилиндрические оболочки, закрепленные по торцам, теряют устойчивость с образованием трех(n=3), четырех(n=4) и более волн смятия рис. б в поперечном сечении
Рис. а.  Рис.б.
Рис.б. 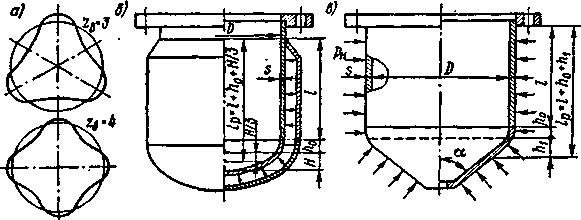
Теоретический расчет для определения критического давления и допускаемого наружного давления [рн]у из условия устойчивости ведется по формулам в зависимости от длины оболочки:
а) для коротких обечаек lp£l0
Если цилиндр короткий и на величину критического давления влияют условия на краях, то критическое давление зависит не только от значения S/D, но и от величины 1/D и определяется по формуле Мизеса
 , где
, где  гдеn – число волн.
гдеn – число волн.
Как видно из формулы в упругой стадии Ркр зависит не от прочности материала, а только от модуля упругости и коэффициента Пуассона.
Ученые Саутуэлл и Папкович преобразовали и упростили данную формулу.
Из уравнения после преобразования получается зависимость
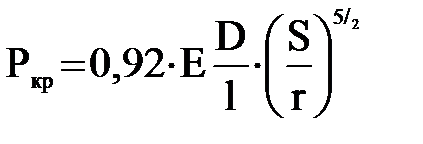
По ГОСТу данное уравнение преобразовано следующим образом вместо S вводится (S-С), числитель и знаменатель умножают на 100.
Тогда формула имеет следующий вид  ;
;
б) для длинных обечаек lp>l0
В этом случае влиянием краевых условий можно пренебречь, а задача сводится к расчету кольца единичной длины, нагруженного равномерно распределенным наружным давлением.
Формула Бресса Грасгоффа:

По ГОСТУ данную формулу преобразуют следующим образом.
Вместо S вводится (S-С), числитель и знаменатель умножают на 100, радиус оболочки заменяют
диаметром r=D/2. В результате таких преобразований получается следующая формула
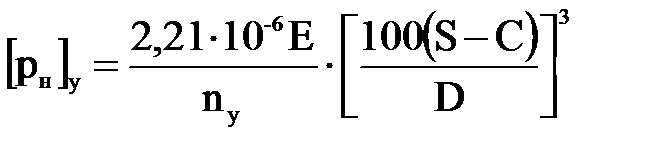 .
.
где Е – модуль продольной упругости материала, МПа;
ny - коэффициент запаса устойчивости.
Анализ данного уравнения показывает, что критическая нагрузка тем больше, чем больше толщина стенки и величина Е, которая характеризует свойства материала и обратно пропорциональна диаметру. Критическая нагрузка не зависит от длины оболочки.
Длинныецилиндрические обечайки и трубы теряют устойчивость с образованием двух волн смятия, т.е. они сплющиваются.
Получаем:
Для коротких Ркр=f( ;
;
Для длинных: Ркр=f( ;
;
Чтобы приложить большую нагрузку можно увеличить толщину стенки, или уменьшить расчетную длинну.
Далее определяется допускаемое наружное давление по формуле

где  - допускаемое наружное давление из условия прочности, которое находится по формуле
- допускаемое наружное давление из условия прочности, которое находится по формуле 
При конструировании химической аппаратуры наиболее часто приходится выполнять расчеты на устойчивость колец жесткости, цилиндрических и конических обечаек, сферических и эллиптических днищ. Кольца жесткости применяются для повышения несущейспособности корпусов тонкостенных аппаратов, сжимаемых наружным давлением
Расчет анкерных болтов
Расчет прочности анкерных болтов производится для сечения Е-Е для условий монтажа ( ), поскольку именно в этих условиях аппарат имеет наименьший вес и, соответственно, осе
), поскольку именно в этих условиях аппарат имеет наименьший вес и, соответственно, осе





 б) Р≤10 МПа (условное разделение)
б) Р≤10 МПа (условное разделение)
 Здесь r – текущий радиус, т.е. значение, при котором необходимо рассчитать напряжение. Величина r может выбираться в пределах от r = a до r = b. Если цилиндрическая обечайка имеет днища, то при действии на них внутреннего и наружного давлений возникает меридиональная сила U и соответственно меридиональное напряжение σm.
Здесь r – текущий радиус, т.е. значение, при котором необходимо рассчитать напряжение. Величина r может выбираться в пределах от r = a до r = b. Если цилиндрическая обечайка имеет днища, то при действии на них внутреннего и наружного давлений возникает меридиональная сила U и соответственно меридиональное напряжение σm.
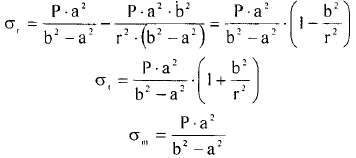
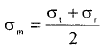
 Как видно, σr, σt для какого то конкретного аппарата (при заданных a,b,P) зависит от текущего радиуса, т.е.
Как видно, σr, σt для какого то конкретного аппарата (при заданных a,b,P) зависит от текущего радиуса, т.е.



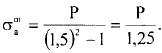


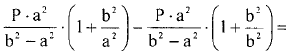


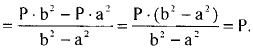

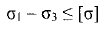




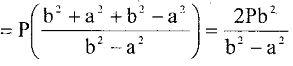 .
.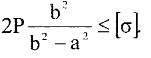




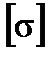 , уравнение не имеет решения. Необходимо повысить несущую способность одним из нижеприведенных способов.
, уравнение не имеет решения. Необходимо повысить несущую способность одним из нижеприведенных способов. и
и  имеют максимальные значения; напряжения по мере удаления от внутренней поверхности снижаются весьма быстро.
имеют максимальные значения; напряжения по мере удаления от внутренней поверхности снижаются весьма быстро. . Гадолин определил:
. Гадолин определил:  с-радиус сопряжения; а- внутренний радиус, b- наружный радиус.
с-радиус сопряжения; а- внутренний радиус, b- наружный радиус.
 n-число слоев,
n-число слоев,  - радиус сопряжения i-го слоя.
- радиус сопряжения i-го слоя.

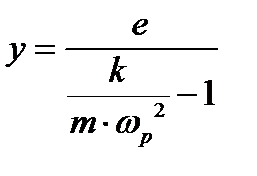
 - рабочая угловая скорость вращения вала;
- рабочая угловая скорость вращения вала; Тогда:
Тогда: 

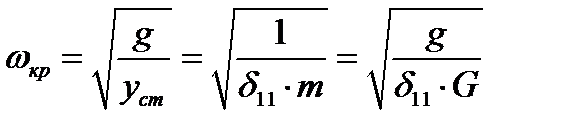
 - единичный прогиб или коэффициент влияния, то есть Yст от единичной поперечной силы;
- единичный прогиб или коэффициент влияния, то есть Yст от единичной поперечной силы; 0,7ωкр
0,7ωкр , может быть представлена в следующем виде:
, может быть представлена в следующем виде: , (9)
, (9) – критическая угловая скорость вала, когда он нагружен только одним грузом массой mi;
– критическая угловая скорость вала, когда он нагружен только одним грузом массой mi;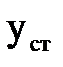 – статический прогиб вала под массой mi, когда он нагружен только этой массой (рисунок 11);
– статический прогиб вала под массой mi, когда он нагружен только этой массой (рисунок 11); Метод Донкерли дает заниженное значение
Метод Донкерли дает заниженное значение 
 , подстановка которых в формулу (10) позволит определить
, подстановка которых в формулу (10) позволит определить  , а, следовательно, и проверить условие виброустойчивости (8).
, а, следовательно, и проверить условие виброустойчивости (8). равна максимальной кинетической энергии системы
равна максимальной кинетической энергии системы  , то есть
, то есть  .
. , (11)
, (11) – статический прогиб вала под грузом массой
– статический прогиб вала под грузом массой 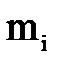 , нагруженного всеми нагрузками (рисунок 12).
, нагруженного всеми нагрузками (рисунок 12). (12)
(12) и частотой, найденной по методу Релея
и частотой, найденной по методу Релея  , то есть:
, то есть: . (13)
. (13)




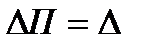 V+
V+  Т
Т Т-работа внешних сил,
Т-работа внешних сил, 
 ; [F]у=
; [F]у=  [М]у=
[М]у= 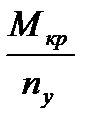 ;
; 10 оболочка рассматривается как длинный стержень, происходит общая потеря устойчивости.
10 оболочка рассматривается как длинный стержень, происходит общая потеря устойчивости. , (3.1)
, (3.1) -формула Эйлера
-формула Эйлера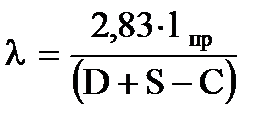 - гибкость оболочки;
- гибкость оболочки; Dcp=D+(S-C);
Dcp=D+(S-C); 
 Допускаемая и критическая осевая сжимающая сила из условия местной потери устойчивости определяется по формуле
Допускаемая и критическая осевая сжимающая сила из условия местной потери устойчивости определяется по формуле ,
, ,
,  );
);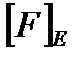 , т.е.
, т.е. 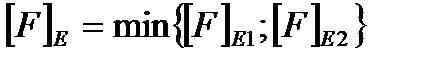 .
. , формула принимает вид
, формула принимает вид .
.
 - допускаемое осевое сжимающее усилие из условия прочности, Н, которое определяется по формуле:
- допускаемое осевое сжимающее усилие из условия прочности, Н, которое определяется по формуле:  .
. Для цилиндра:
Для цилиндра: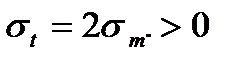





 -наружного давления (вакуумная колонна, аппарат с рубашкой, трубопроводы под водой);
-наружного давления (вакуумная колонна, аппарат с рубашкой, трубопроводы под водой);
 ,[F] =
,[F] =  [М] =
[М] =  ,
, ;
; ;
;
 ,
, ,
, Рис.б.
Рис.б. 
 , где
, где  гдеn – число волн.
гдеn – число волн.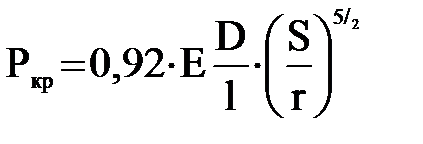
 ;
;
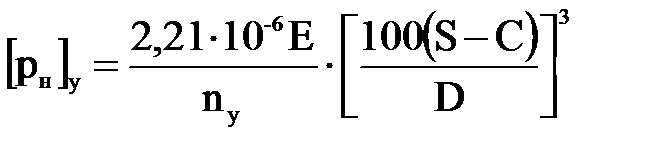 .
. ;
; ;
;
 - допускаемое наружное давление из условия прочности, которое находится по формуле
- допускаемое наружное давление из условия прочности, которое находится по формуле 
 ), поскольку именно в этих условиях аппарат имеет наименьший вес и, соответственно, осе
), поскольку именно в этих условиях аппарат имеет наименьший вес и, соответственно, осе


