v(Si)- вес элемента S;
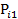 …
…  – выборка свойств из Р1 …РN
– выборка свойств из Р1 …РN
V(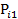 …
…  ) – сумма весов элементов, обладающих всеми из заданных свойств.
) – сумма весов элементов, обладающих всеми из заданных свойств.
 сумма весов для всех выборок
сумма весов для всех выборок


(ps последняя формула не точно, общий материал взят из леций Гусева)
Принцип включения и исключения. Теорема о числе элементов, обладающих в точности R-свойствами из N–множества свойств. Доказательство.
Теорема:
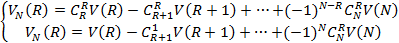
Доказательство.
Пусть некоторый элемент  i
i  имеет вес v(Si) и удовлетворяет в точности t свойствам pi1…pit из R.
имеет вес v(Si) и удовлетворяет в точности t свойствам pi1…pit из R.
Возможно 3 случая
1. t< R вес этого элемента в подсчете не участвуют, вносится 0
2. t=R в правую часть вносит свой собственный вес
3. t> R вносит свой вес v(Si):

Так как: 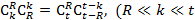 )
)

Тогда выражение в скобках равно 0, так как оно является частным случаем разложением бинома Ньютона.


13. Задача о беспорядках. Теорема о числе беспорядков из элементов
n–множества. Доказательство. Следствия.
Пусть имеется конечное упорядоченное множество элементов {1,…, n }. Из этих элементов могут быть образованы перестановки a 1,…, an (ai Î{1,…, n }). Число всех возможных перестановок – n!. Среди этих n! перестановок есть такие, что ни один элемент не стоит на своём месте (ai ¹ i, i = 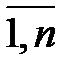 ). Иначе говоря, элемент номер 1 не стоит на 1-ом месте, элемент номер 2 не стоит на 2-м месте, и т.д., элемент номер n не стоит на n -м месте. Такие перестановки называются беспорядками.
). Иначе говоря, элемент номер 1 не стоит на 1-ом месте, элемент номер 2 не стоит на 2-м месте, и т.д., элемент номер n не стоит на n -м месте. Такие перестановки называются беспорядками.
Число беспорядков из n элементов обозначается Dn (ясно, что Dn<n!).
Теорема. Число беспорядков из n элементов равно:
 .
.
Доказательство
Обозначим через свойство pi – «i -й элемент стоит на i -м месте». Тогда по формуле решета  .
.
Общее число перестановок n элементов – n! Число перестановок, где i -й элемент стоит на i -м месте, равно (n -1)! (ставим i -й элемент на i -е место, а оставшиеся n -1 элементы переставляем (n -1)! способами). При этом сам i -й элемент можно выбрать  способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно
способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно  .
.
Число перестановок, где i -й элемент стоит на i -м месте, а j -й на j -м (i ¹ j), равно (n -2)!, при этом i -й и j -й элементы можно выбрать  способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах –
способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах –  .
.
Аналогично, число перестановок, где на своих местах стоят хотя бы три элемента –  . Число перестановок, где на своих местах стоят хотя бы r элементов –
. Число перестановок, где на своих местах стоят хотя бы r элементов –  . Число перестановок, где все элементы стоят на своих местах
. Число перестановок, где все элементы стоят на своих местах  . Подставляем в формулу решета:
. Подставляем в формулу решета: 
Следствие 1.
Так как  ,
,
то  .
.
Следствие 2.
Так как 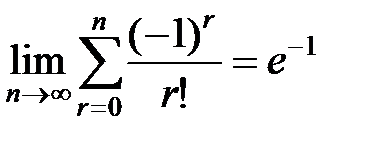 , то
, то  .
.
Функция Эйлера
Функция Эйлера φ (n), где n – натуральное число, дает количество натуральных чисел, не превышающих n и взаимно простых с n. Иначе говоря, φ (n)= k, где 0< k £ n; (k, n)=1.
Теорема
 , где pi – все простые делители n. (
, где pi – все простые делители n. ( - произведение по всем простым делителям числа n).
- произведение по всем простым делителям числа n).
# В теореме Лежандра заменим ai на pi, где pi – простые делители n.
Тогда  (так как pi делят n нацело).
(так как pi делят n нацело).
По теореме Лежандра

 . #
. #
Пример. Определим, сколько чисел, не превышающих 100, взаимно простые с 100. Разложим число 100 на простые сомножители: 100=2·2·5·5=2252. Таким образом, у числа 100 два простых делителя – 2 и 5. По формуле Эйлера получаем
 .
.
Таким образом, среди первой сотни есть 40 чисел, взаимно простых с 100.
Функция Мебиуса
Функция Мебиуса m (n), где n – натуральное число, принимает следующие значения:

Функция Мебиуса позволяет записать функцию Эйлера в виде суммы:
 .
.
Суммирование идет по всем делителям n (а не только по простым делителям).
Пример. Вычислим φ (100), используя функцию Мебиуса.
Все делители 100 – {1, 2, 4, 5, 10, 20, 25, 50, 100}.
m (1) = 1,
m (2) = (-1)1 = -1 (у двойки один простой делитель – 2)
m (4) = 0 (4 делится на квадрат двойки)
m (5) = (-1)1 = -1 (у 5 один простой делитель – 5)
m (10) = (-1)2 = 1 (у 10 два простых делителя – 2 и 5)
m (20) = 0 (20 делится на квадрат двойки)
m (25) = 0 (25 делится на квадрат пятерки)
m (50) = 0 (50 делится и на 22, и на 55)
m (100) = 0 (100 делится и на 22, и на 55)
Таким образом,

Свойство функции Мебиуса:  .
.
Например, n =100, a Î{1, 2, 4, 5, 10, 20, 25, 50, 100}.
 .
.
16 Теорема о числе способов выбора k-элементов, среди которых нет двух соседних, из n элементов, расположенных в ряд. Доказать с помощью получения рекуррентной формулы.



 …
…  – выборка свойств из Р1 …РN
– выборка свойств из Р1 …РN сумма весов для всех выборок
сумма весов для всех выборок

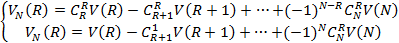
 i
i  имеет вес v(Si) и удовлетворяет в точности t свойствам pi1…pit из R.
имеет вес v(Si) и удовлетворяет в точности t свойствам pi1…pit из R.
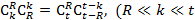 )
)


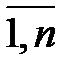 ). Иначе говоря, элемент номер 1 не стоит на 1-ом месте, элемент номер 2 не стоит на 2-м месте, и т.д., элемент номер n не стоит на n -м месте. Такие перестановки называются беспорядками.
). Иначе говоря, элемент номер 1 не стоит на 1-ом месте, элемент номер 2 не стоит на 2-м месте, и т.д., элемент номер n не стоит на n -м месте. Такие перестановки называются беспорядками. .
. .
. способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно
способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно  .
. способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах –
способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах –  .
. . Число перестановок, где на своих местах стоят хотя бы r элементов –
. Число перестановок, где на своих местах стоят хотя бы r элементов –  . Число перестановок, где все элементы стоят на своих местах
. Число перестановок, где все элементы стоят на своих местах  . Подставляем в формулу решета:
. Подставляем в формулу решета: 
 ,
, .
.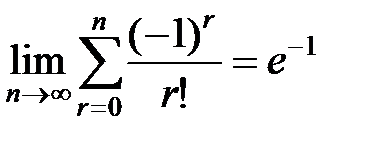 , то
, то  .
. , где pi – все простые делители n. (
, где pi – все простые делители n. ( - произведение по всем простым делителям числа n).
- произведение по всем простым делителям числа n). (так как pi делят n нацело).
(так как pi делят n нацело).
 . #
. # .
.
 .
.
 .
. .
.


