Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Числа Стирлинга первого рода (без знака) — количество перестановок порядка n с k циклами.
Определение
Числами Стирлинга первого рода (со знаком) s(n, k) называются коэффициенты многочлена:

где (x) n — символ Похгаммера (убывающий факториал):

Как видно из определения, числа имеют чередующийся знак. Их абсолютные значения задают количество перестановок множества, состоящего из n элементов с k циклами.
Рекуррентное соотношение
Числа Стирлинга первого рода задаются рекуррентным соотношением:
s (n, n) = 1, для n ≥ 0,
s (n,0) = 0, для n > 0,
 для 0 < k < n.
для 0 < k < n.
Доказательство.
Для n =1 это равенство проверяется непосредственно. Пусть перестановка (n -1)-го порядка распадается на k циклов. Число n можно добавить после любого числа в соответствующий цикл. Все полученные перестановки — различные и содержат k циклов, их количество (n -1)· s (n -1, k). Из любой перестановки (n -1)-го порядка, содержащей k -1 цикл, можно сформировать единственную перестановку n порядка, содержащую k циклов, добавив цикл образованный единственным числом n. Очевидно, что эта конструкция описывает все перестановки n -го порядка, содержащие k циклов. Тем самым равенство доказано.
Пример
Первые ряды:
| n\k
|
|
|
|
|
|
|
|
|
|
| | | | | | |
|
|
|
| | | | | |
|
|
| −1
|
| | | | |
|
|
|
| −3
|
| | | |
|
|
| −6
|
| −6
|
| | |
|
|
|
| −50
|
| −10
|
| |
|
|
| −120
|
| −225
|
| −15
|
|
| | | | | | | | |
В комбинаторике числом Стирлинга второго рода из n по k, обозначаемым  или
или  , называется количество неупорядоченных разбиений n -элементного множества на k непустых подмножеств.
, называется количество неупорядоченных разбиений n -элементного множества на k непустых подмножеств.
Рекуррентная формула
Числа Стирлинга второго рода удовлетворяют рекуррентному соотношению:
 , для n ≥ 0,
, для n ≥ 0,
 , для n > 0,
, для n > 0,
 для
для 
Явная формула

Пример
Начальные значения чисел Стирлинга второго рода приведены в таблице:
Свойства
Биективным отображением называется отображение, обладающее признаками инъективности и сюръективности одновременно.
Биекция
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 февраля 2012; проверки требуют 2 правки.


Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 февраля 2012; проверки требуют 2 правки.
Перейти к: навигация, поиск


Биективная функция.
Биекция — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением.
Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы.
Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества).
Определение
Функция  называется биекцией (и обозначается
называется биекцией (и обозначается  ), если она:
), если она:
- Переводит разные элементы множества
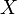 в разные элементы множества
в разные элементы множества  (инъективность). Иными словами,
(инъективность). Иными словами, -
 .
.
- Любой элемент из
 имеет свой прообраз (сюръективность). Иными словами,
имеет свой прообраз (сюръективность). Иными словами, -
 .
.
Примеры
- Тождественное отображение
 на множестве
на множестве 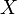 биективно.
биективно. -
 — биективные функции из
— биективные функции из  в себя. Вообще, любой моном одной переменнойнечетнойстепени является биекцией из
в себя. Вообще, любой моном одной переменнойнечетнойстепени является биекцией из  в себя.
в себя. -
 — биективная функция из
— биективная функция из  в
в  .
. -
 не является биективной функцией, если считать её определённой на всём
не является биективной функцией, если считать её определённой на всём  .
.
Свойства


Композиция инъекции и сюръекции, дающая биекцию.
- Функция
 является биективной тогда и только тогда, когда существует обратная функция
является биективной тогда и только тогда, когда существует обратная функция  такая, что
такая, что
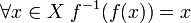 и
и 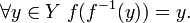
- Если функции
 и
и  биективны, то и композиция функций
биективны, то и композиция функций  биективна, в этом случае
биективна, в этом случае  . Коротко: композиция биекций является биекцией. Обратное, однако, неверно: если
. Коротко: композиция биекций является биекцией. Обратное, однако, неверно: если  биективна, то мы можем утверждать лишь, что
биективна, то мы можем утверждать лишь, что  инъективна, а
инъективна, а  сюръективна.
сюръективна.
Применения
В информатике
Организация связи «один к одному» между таблицамиреляционной БД на основе первичных ключей.
Числа Каталана
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
ЧислаКатала́на — числовая последовательность, встречающаяся во многих задачах комбинаторики. Последовательность названа в честь бельгийского математика Каталана, хотя была известна ещё Л. Эйлеру.
Первые несколько чисел Каталана:
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, … (последовательность A000108 в OEIS)
Определения
n -е число Каталана  можно определить одним из следующих способов:
можно определить одним из следующих способов:
- Количество разбиений выпуклого (n +2)-угольника на треугольники непересекающимися диагоналями.
- Количество правильных скобочных последовательностей длины 2 n, то есть таких последовательностей из n левых и n правых скобок, в которых количество открывающих скобок равно количеству закрывающих, и в любом её префиксе открывающих скобок не меньше, чем закрывающих.
Например, для n =3 существует 5 таких последовательностей:
((())), ()(()), ()()(), (())(), (()())
то есть 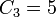 .
.
- Количество способов соединения 2 n точек на окружности n непересекающимися хордами.
- Количество неизоморфных упорядоченных бинарных деревьев с корнем и n +1 листьями.
Свойства
- Числа Каталана удовлетворяют рекуррентному соотношению:
 и
и  для
для 
Это соотношение легко получается из того, что любая непустая правильная скобочная последовательность однозначно представима в виде w =(w 1) w 2, где w 1, w 2 — правильные скобочные последовательности.
- Производящая функция чисел Каталана равна:

- Числа Каталана можно выразить через биномиальные коэффициенты:

Другими словами, число Каталана  равно разности центрального биномиального коэффициента и соседнего с ним в той же строке треугольника Паскаля.
равно разности центрального биномиального коэффициента и соседнего с ним в той же строке треугольника Паскаля.
- Асимптотически

Чтобы не ограничиваться одной только ссылкой, напишу приведенный в "Конкретной математике" вывод формулы для чисел Каталана. Красивое и очень простое рассуждение.
Определение (одно из многих). Числом Каталана Cn называется количество последовательностей длины (2n+1) a0, a1,..., a2n, составленных из +1 и -1, таких что сумма чисел равна +1, а все частичные суммы
a0, a0+a1,..., a0+...+a2n
положительны.
Лемма Рени. Если x1, x2,..., xm - любая последовательность целых чисел, сумма которых равна +1, то ровно у одного из её циклических сдвигов
x1, x2,..., xm
x2,..., xm, x1
xm, x1,..., xm-1
частичные суммы все положительны.
Доказательство. Продолжим последовательность периодически до бесконечной последовательности: xm+k=xk, для всех k>0. Если для этой бесконечной последовательности нарисовать график частичных сумм sn=x1+...+xn, то он будет иметь "средний наклон" 1/m, поскольку sn+m=sn+1. Весь график может быть заключён между двумя прямыми наклона 1/m. Эти прямые касаются графика ровно один раз на каждом периоде из m точек, поскольку прямые с наклоном 1/m могут проходить через точки с целыми координатами только один раз на m единиц. Единственная нижняя точка касания-- это то единственное место в цикле, начиная с которого все частные суммы будут положительны.
Подсчёт последовательностей из +1 и -1 с общей суммой +1.
Всего есть C2n+1n последовательностей, содержащих n элементов -1 и (n+1) элементов +1. Построим все C2n+1n последовательностей и все (2n+1) их циклических сдвигов в виде таблицы из C2n+1n строк и (2n+1) столбцов. Очевидно, что каждая последовательность встречается в таблице (2n+1) раз, по одному разу в каждом столбце. По лемме Рени в каждой строке содержится ровно одна последовательность с положительными частичными суммами. Таким образом, всего в таблице искомые последовательности встречается C2n+1n раз. Каждая встречается (2n+1) раз. Следовательно
Cn = C2n+1n/(2n+1) = C2nn/(n+1).
28) Биномиальный коэффициент
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
В математике биномиальные коэффициенты — это коэффициенты в разложениибинома Ньютона 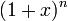 по степеням x. Коэффициент при
по степеням x. Коэффициент при  обозначается
обозначается  (иногда
(иногда  ) и читается «биномиальный коэффициент из n по k» (или «це из n по k»):
) и читается «биномиальный коэффициент из n по k» (или «це из n по k»):
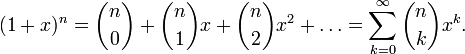
В комбинаторике биномиальный коэффициент  интерпретируется как количество сочетаний из n по k, то есть количество всех подмножеств (выборок) размера k в n -элементном множестве.
интерпретируется как количество сочетаний из n по k, то есть количество всех подмножеств (выборок) размера k в n -элементном множестве.
Биномиальные коэффициенты часто возникают в задачах комбинаторики и теории вероятностей. Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.
Явные формулы
Значение биномиального коэффициента  определено для всех целых чисел n и k. Явные формулы для вычисления биномиальных коэффициентов:
определено для всех целых чисел n и k. Явные формулы для вычисления биномиальных коэффициентов:
 для
для 
 для
для  или
или 
 для
для 
где  обозначает факториал числа m.
обозначает факториал числа m.
Треугольник Паскаля
Тождество

позволяет расположить биномиальные коэффициенты для неотрицательных целых чисел n, k в виде треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих:

Треугольная таблица, предложенная Паскалем в «Трактате об арифметическом треугольнике» (1654), отличается от выписанной здесь поворотом на 45°. Таблицы для изображения биномиальных коэффициентов были известны и ранее (Тарталье, О. Хайяму и др.).
Строки в треугольнике Паскаля в пределе стремятся к функции нормального распределения.
Если взять квадратную матрицу, отсчитав N элементов по катетам треугольника и повернув квадрат на любой из четырёх углов, то детерминант этих четырёх матриц по модулю равен 1 при любом N. Если поставить уголом из 1 в верхний левый угол, то детерминант матрицы будет равен 1.
В матрице  числа на диагонали i+j = const повторяют числа строк треугольника Паскаля. (i,j = 0...∞)
числа на диагонали i+j = const повторяют числа строк треугольника Паскаля. (i,j = 0...∞)
Матрицу  где i, j = 0…p можно разложить в произведение двух строго диагональных матриц. Первая нижнетреугольная, а вторая получается из первой путем транcпонирования. Элементы такой матрицы
где i, j = 0…p можно разложить в произведение двух строго диагональных матриц. Первая нижнетреугольная, а вторая получается из первой путем транcпонирования. Элементы такой матрицы 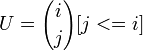
 где i,j = 0...p Далее обратная матрица к U
где i,j = 0...p Далее обратная матрица к U
 таким образом можно разложить обратную матрицу к
таким образом можно разложить обратную матрицу к  в произведение двух строго диагональных матриц и дать явное выражение для обратных элементов. Первая верхнетреугольная, а вторая получается из первой путем транспонирования.
в произведение двух строго диагональных матриц и дать явное выражение для обратных элементов. Первая верхнетреугольная, а вторая получается из первой путем транспонирования.
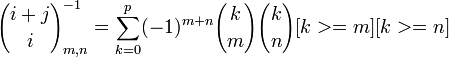 i,j,m,n = 0...p, если выражение в кваратных скобках ложно, то элемент суммы равен 0. Элементы обратной матрицы меняются при изменение её размера и в отличие от матрицы
i,j,m,n = 0...p, если выражение в кваратных скобках ложно, то элемент суммы равен 0. Элементы обратной матрицы меняются при изменение её размера и в отличие от матрицы  недостаточно приписать новую строку и столбец.
недостаточно приписать новую строку и столбец.
Свойства
Производящие функции
Для фиксированного значения n производящей функцией последовательности биномиальных коэффициентов  является:
является:
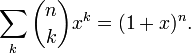
Для фиксированного значения k производящей функцией последовательности биномиальных коэффициентов  является:
является:
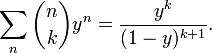
Двумерной производящей функцией биномиальных коэффициентов является:

Делимость
Из теоремы Люка следует, что:
-
 нечётен
нечётен  в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули.
в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули. -
 некратен простому p
некратен простому p  в p -ичной записи числа k все разряды не превосходят соответствующих разрядов числа n.
в p -ичной записи числа k все разряды не превосходят соответствующих разрядов числа n. - В последовательности биномиальных коэффициентов
 :
: - все числа не кратны заданному простому p

 , где натуральное число m < p;
, где натуральное число m < p; - все числа, кроме первого и последнего, кратны заданному простому p

 ;
; - количество нечётных чисел равно степени двойки (степень двойки равна количеству единиц в двоичной записи числа n);
- не может быть поровну чётных и нечётных чисел;
- количество не кратных простому p чисел равно
 , где числа
, где числа  — разряды p -ичной записи числа n; а число
— разряды p -ичной записи числа n; а число  — её длина.
— её длина.
Тождества
-

-
 (правило симметрии).
(правило симметрии). -

- Следствия тождества
 :
: -
 для
для  .
. -
 Это тождество можно усилить
Это тождество можно усилить -
 0<a<n
0<a<n -
 a>=n
a>=n -
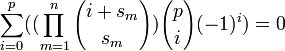 если
если  — более общий вид тождества выше.
— более общий вид тождества выше. -

-

-
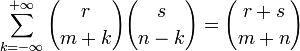 (свёртка Вандермонда).
(свёртка Вандермонда). -
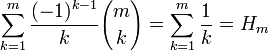 — m -оегармоническое число.
— m -оегармоническое число. - Мультисекция ряда
 даёт тождество, выражающее сумму биномиальных коэффициентов с произвольным шагом s и смещением t
даёт тождество, выражающее сумму биномиальных коэффициентов с произвольным шагом s и смещением t  в виде замкнутой суммы из s слагаемых:
в виде замкнутой суммы из s слагаемых:

Асимптотика и оценки
где 
Алгоритмы вычисления
Биномиальные коэффициенты могут быть вычислены с помощью формулы  , если на каждом шаге хранить значения
, если на каждом шаге хранить значения  при
при  . Этот алгоритм особенно эффективен, если нужно получить все значения
. Этот алгоритм особенно эффективен, если нужно получить все значения  при фиксированном
при фиксированном  . Алгоритм требует
. Алгоритм требует  памяти (
памяти (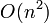 при вычислении всей таблицы биномиальных коэффициентов) и
при вычислении всей таблицы биномиальных коэффициентов) и 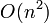 времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени).
времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени).
При фиксированном значении k биномиальные коэффициенты могут быть вычислены по рекуррентной формуле  с начальным значением
с начальным значением 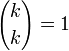 . Для вычисления значения
. Для вычисления значения  этот метод требует
этот метод требует  памяти и
памяти и  времени.
времени.





 для 0 < k < n.
для 0 < k < n. или
или  , называется количество неупорядоченных разбиений n -элементного множества на k непустых подмножеств.
, называется количество неупорядоченных разбиений n -элементного множества на k непустых подмножеств. , для n ≥ 0,
, для n ≥ 0, , для n > 0,
, для n > 0, для
для 

 где
где 

 — число Белла.
— число Белла.



 называется биекцией (и обозначается
называется биекцией (и обозначается  ), если она:
), если она: в разные элементы множества
в разные элементы множества  (инъективность). Иными словами,
(инъективность). Иными словами,  .
. .
. на множестве
на множестве  — биективные функции из
— биективные функции из  в себя. Вообще, любой моном одной переменнойнечетнойстепени является биекцией из
в себя. Вообще, любой моном одной переменнойнечетнойстепени является биекцией из  — биективная функция из
— биективная функция из  .
. не является биективной функцией, если считать её определённой на всём
не является биективной функцией, если считать её определённой на всём 
 такая, что
такая, что и
и 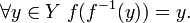
 и
и  биективны, то и композиция функций
биективны, то и композиция функций  биективна, в этом случае
биективна, в этом случае  . Коротко: композиция биекций является биекцией. Обратное, однако, неверно: если
. Коротко: композиция биекций является биекцией. Обратное, однако, неверно: если  можно определить одним из следующих способов:
можно определить одним из следующих способов: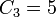 .
. и
и  для
для 



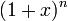 по степеням x. Коэффициент при
по степеням x. Коэффициент при  обозначается
обозначается  (иногда
(иногда  ) и читается «биномиальный коэффициент из n по k» (или «це из n по k»):
) и читается «биномиальный коэффициент из n по k» (или «це из n по k»):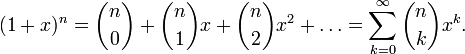
 для
для 
 для
для  или
или 
 для
для 
 обозначает факториал числа m.
обозначает факториал числа m.

 числа на диагонали i+j = const повторяют числа строк треугольника Паскаля. (i,j = 0...∞)
числа на диагонали i+j = const повторяют числа строк треугольника Паскаля. (i,j = 0...∞)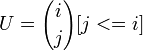
 где i,j = 0...p Далее обратная матрица к U
где i,j = 0...p Далее обратная матрица к U таким образом можно разложить обратную матрицу к
таким образом можно разложить обратную матрицу к 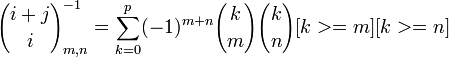 i,j,m,n = 0...p, если выражение в кваратных скобках ложно, то элемент суммы равен 0. Элементы обратной матрицы меняются при изменение её размера и в отличие от матрицы
i,j,m,n = 0...p, если выражение в кваратных скобках ложно, то элемент суммы равен 0. Элементы обратной матрицы меняются при изменение её размера и в отличие от матрицы  является:
является: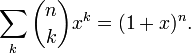
 является:
является: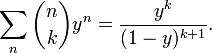

 в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули.
в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули. :
:  , где натуральное число m < p;
, где натуральное число m < p; ;
; , где числа
, где числа  — разряды p -ичной записи числа n; а число
— разряды p -ичной записи числа n; а число  — её длина.
— её длина.
 (правило симметрии).
(правило симметрии).
 :
: 

 для
для  .
. Это тождество можно усилить
Это тождество можно усилить 0<a<n
0<a<n a>=n
a>=n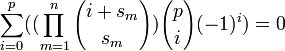 если
если  — более общий вид тождества выше.
— более общий вид тождества выше.

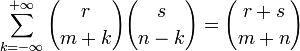 (свёртка Вандермонда).
(свёртка Вандермонда).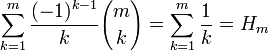 — m -оегармоническое число.
— m -оегармоническое число. в виде замкнутой суммы из s слагаемых:
в виде замкнутой суммы из s слагаемых:

 при
при 
 , при
, при 


 , если на каждом шаге хранить значения
, если на каждом шаге хранить значения  при
при  . Этот алгоритм особенно эффективен, если нужно получить все значения
. Этот алгоритм особенно эффективен, если нужно получить все значения  . Алгоритм требует
. Алгоритм требует  памяти (
памяти ( при вычислении всей таблицы биномиальных коэффициентов) и
при вычислении всей таблицы биномиальных коэффициентов) и  с начальным значением
с начальным значением 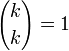 . Для вычисления значения
. Для вычисления значения  памяти и
памяти и 

