Задача о покрытии
Найти такие множества Ti, i = 1, 2, …, r, чтобы  (чтобы объединение этих множеств «покрыло» S). Например, застелить весь пол в комнате несколькими коврами. Ковры могут накладываться друг на друга (множества могут пересекаться), но незакрытых участков поФла быть не должно.
(чтобы объединение этих множеств «покрыло» S). Например, застелить весь пол в комнате несколькими коврами. Ковры могут накладываться друг на друга (множества могут пересекаться), но незакрытых участков поФла быть не должно.
Во многих задачах покрытие должно быть наиболее экономичным (так называемое минимальное покрытие), когда число множеств Ti должно быть минимальным, сами они должны содержать минимально возможное число элементов.
Задача об укладке
Найти такие попарно непересекающиеся множества Ti, i = 1, 2, …, r, (Ti Ç Tj = Æ при i ¹ j) чтобы  (чтобы объединение этих множеств вошло в S).
(чтобы объединение этих множеств вошло в S).
Например, уложить несколько предметов в одну коробку. Между предметами могут быть пустые промежутки, но сами предметы друг с другом не пересекаются и укладываются в коробку.
Во многих задачах укладка должна быть наиболее экономичной, когда укладывается максимально возможное количество предметов, а количество пустых промежутков должно быть как можно меньше.
Задача о разбиении
Найти такие попарно непересекающиеся множества Ti, i = 1, 2, …, r, (Ti Ç Tj = Æ при i ¹ j) чтобы  (чтобы объединение этих непересекающихся множеств дало S).
(чтобы объединение этих непересекающихся множеств дало S).
Например, группы в институте – это разбиение множества студентов института. Группы не пересекаются, а их объединение дает множество всех студентов института.
Теорема о числе разбиений элементов множества на 2, 3, …,k классов, без учета их порядка в классах и без ограничений на занятость класса.
Теорема заключается в том, что данное число равно:

В лекции давалась задача о кольцах (сколькими способами можно одеть на пальцы одной руки 7 колец). Вот нечто подобное с доказательством:
Есть k ящиков и n>=k однаковых шаров. Сколькими способами можно разложить шары по ящикам, если могут быть пустые ящики?
Решение
Давайте определять раскладку так: выложим шары в ряд и поставим между ними k-1 перегородку. То, что слева от первой перегородки, положим в первый ящик, между первой и второй - во второй... то, что справа от последней - в последний, k-й ящик. Ящик будет пустым, только если две перегородки стоят рядом не разделенные шарами, либо перегородка стоит с краю, левее или правее всех шаров. Шары и перегородки можно ставить в произвольном порядке. Давайте считать, что у нас расставлено в ряд n+k-1 объектов: n из них шары, а остальные - перегородки. Тогда раскладка будет определяться тем, на каких местах какие объекты стоят. Из n+k-1 мест можно выбрать n мест для шаров Cn+k-1n способами, или: k-1 место для перегородок Cn+k-1k-1 способами. Эти числа равны и оба являются ответом.
7. Комбинаторные задачи о покрытиях, укладках, разбиениях. Примеры. Теорема о числе разбиений элементов множества на 2, 3, …, k классов, с учетом их порядка в классах и без ограничений на занятость класса. Доказательства. Следствия.
… смотри предыдущий вопрос
Теорема (PS лекции Гусева)
Пусть мы рассматриваем упорядоченные разбиения n-множества на k-подмножеств Ti.

(R1, R2,…,Rk) полиноминальные коэффициенты

Доказательство

Следствие
R сочетаний без повторений из n множества можно интерпретировать как (R, n-R)
Пример: разбиение «Комбинаторика»
К 2
О 2
М 1
Б 1
И 2
Н 1
А 2
Т 1
О
Р 1
И
К
А
Р13 (221121121)=13!/2!2!1!...1!
Интерпретация комбинаторных операций выборки и упорядочивания как отображения множеств. Примеры. Сформулировать и доказать теорему о числе различных отображений N в K. Условие существования взаимно-однозначных отображений.
Доказательство
Обозначим через свойство pi – «i -й элемент стоит на i -м месте». Тогда по формуле решета  .
.
Общее число перестановок n элементов – n! Число перестановок, где i -й элемент стоит на i -м месте, равно (n -1)! (ставим i -й элемент на i -е место, а оставшиеся n -1 элементы переставляем (n -1)! способами). При этом сам i -й элемент можно выбрать  способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно
способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно  .
.
Число перестановок, где i -й элемент стоит на i -м месте, а j -й на j -м (i ¹ j), равно (n -2)!, при этом i -й и j -й элементы можно выбрать  способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах –
способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах –  .
.
Аналогично, число перестановок, где на своих местах стоят хотя бы три элемента –  . Число перестановок, где на своих местах стоят хотя бы r элементов –
. Число перестановок, где на своих местах стоят хотя бы r элементов –  . Число перестановок, где все элементы стоят на своих местах
. Число перестановок, где все элементы стоят на своих местах  . Подставляем в формулу решета:
. Подставляем в формулу решета: 
Следствие 1.
Так как  ,
,
то  .
.
Следствие 2.
Так как 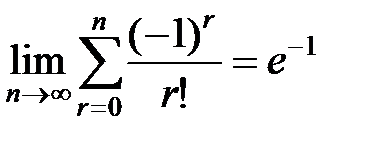 , то
, то  .
.
Функция Эйлера
Функция Эйлера φ (n), где n – натуральное число, дает количество натуральных чисел, не превышающих n и взаимно простых с n. Иначе говоря, φ (n)= k, где 0< k £ n; (k, n)=1.
Теорема
 , где pi – все простые делители n. (
, где pi – все простые делители n. ( - произведение по всем простым делителям числа n).
- произведение по всем простым делителям числа n).
# В теореме Лежандра заменим ai на pi, где pi – простые делители n.
Тогда  (так как pi делят n нацело).
(так как pi делят n нацело).
По теореме Лежандра

 . #
. #
Пример. Определим, сколько чисел, не превышающих 100, взаимно простые с 100. Разложим число 100 на простые сомножители: 100=2·2·5·5=2252. Таким образом, у числа 100 два простых делителя – 2 и 5. По формуле Эйлера получаем
 .
.
Таким образом, среди первой сотни есть 40 чисел, взаимно простых с 100.
Функция Мебиуса
Функция Мебиуса m (n), где n – натуральное число, принимает следующие значения:

Функция Мебиуса позволяет записать функцию Эйлера в виде суммы:
 .
.
Суммирование идет по всем делителям n (а не только по простым делителям).
Пример. Вычислим φ (100), используя функцию Мебиуса.
Все делители 100 – {1, 2, 4, 5, 10, 20, 25, 50, 100}.
m (1) = 1,
m (2) = (-1)1 = -1 (у двойки один простой делитель – 2)
m (4) = 0 (4 делится на квадрат двойки)
m (5) = (-1)1 = -1 (у 5 один простой делитель – 5)
m (10) = (-1)2 = 1 (у 10 два простых делителя – 2 и 5)
m (20) = 0 (20 делится на квадрат двойки)
m (25) = 0 (25 делится на квадрат пятерки)
m (50) = 0 (50 делится и на 22, и на 55)
m (100) = 0 (100 делится и на 22, и на 55)
Таким образом,

Свойство функции Мебиуса:  .
.
Например, n =100, a Î{1, 2, 4, 5, 10, 20, 25, 50, 100}.
 .
.
16 Теорема о числе способов выбора k-элементов, среди которых нет двух соседних, из n элементов, расположенных в ряд. Доказать с помощью получения рекуррентной формулы.
Подстановка
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Это статья о подстановке как о синтаксической операции над термами. Возможно, вас интересует перестановка.
В математике и компьютерных науках подстановка — это операция синтаксической замены подтермов данного терма другими термами, согласно определённым правилам. Обычно речь идёт о подстановке терма вместо переменной.
Содержание
- 1 Определения и обозначения
- 2 Подстановка переменной в λ-исчислении
- 3 Подстановка переменной в программировании
- 4 См. также
- 5 Ссылки
|
Определения и обозначения
Для подстановки не существует универсальной, согласованной нотации, равно как и стандартного определения. Понятие подстановки варьируется не только в рамках разделов, но и на уровне отдельных публикаций. В целом, можно выделить контекстную подстановку и подстановку «вместо». В первом случае место в терме, где происходит замена, задаётся контекстом, то есть частью терма, «окружающим» это место. В частности, такое понятие подстановки используется в переписывании. Второй вариант более распространён. В этом случае подстановка обычно задаётся некоторой функцией  из множества переменных в множество термов. Для обозначения действия подстановки, как правило, используют постфиксную нотацию. Например,
из множества переменных в множество термов. Для обозначения действия подстановки, как правило, используют постфиксную нотацию. Например,  означает результат действия подстановки
означает результат действия подстановки  на терм
на терм  .
.
В подавляющем большинстве случаев требуется чтобы подстановка имела конечный носитель, то есть, чтобы множество  было конечным. В таком случае её можно задать простым перечислением пар «переменная-значение». Поскольку каждую такую подстановку можно свести к последовательности подстановок, замещающих всего по одной переменной каждая, не ограничивая общности можно считать, что подстановка задаётся одной парой «переменная-значение», что обычно и делается.
было конечным. В таком случае её можно задать простым перечислением пар «переменная-значение». Поскольку каждую такую подстановку можно свести к последовательности подстановок, замещающих всего по одной переменной каждая, не ограничивая общности можно считать, что подстановка задаётся одной парой «переменная-значение», что обычно и делается.
Последнее определение подстановки является, видимо, самым типичным и часто используемым. Однако и для него не существует единой общепринятой нотации. Наиболее часто для обозначения подстановки a вместо x в t используется запись t [ a / x ], t [ x:= a ] или t [ x ← a ].
Подстановка переменной в λ-исчислении
В λ-исчислении, подстановка определяется структурной индукцией. Для произвольных объектов  ,
,  и произвольной переменной
и произвольной переменной  результат замещения произвольного свободного вхождения
результат замещения произвольного свободного вхождения  в
в  считается подстановкой и определяется индукцией по построению
считается подстановкой и определяется индукцией по построению  :
:
(i) базис:  : объект
: объект  совпадает с переменной
совпадает с переменной  . Тогда
. Тогда  ;
;
(ii) базис:  : объект
: объект  совпадает с константой
совпадает с константой  . Тогда
. Тогда  для произвольных атомарных
для произвольных атомарных  ;
;
(iii) шаг:  : объект
: объект  неатомарный и имеет вид аппликации
неатомарный и имеет вид аппликации  . Тогда
. Тогда  ;
;
(iv) шаг:  : объект
: объект  неатомарный и является
неатомарный и является  -абстракцией
-абстракцией  . Тогда [
. Тогда [  ;
;
(v) шаг:  : объект
: объект  неатомарный и является
неатомарный и является  -абстракцией
-абстракцией  , причем
, причем  . Тогда:
. Тогда:
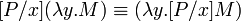 для
для  и
и  или
или 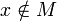 ;
;
 для
для  и
и 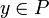 и
и 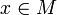 .
.
Определение
Числами Стирлинга первого рода (со знаком) s(n, k) называются коэффициенты многочлена:

где (x) n — символ Похгаммера (убывающий факториал):

Как видно из определения, числа имеют чередующийся знак. Их абсолютные значения задают количество перестановок множества, состоящего из n элементов с k циклами.
Рекуррентное соотношение
Числа Стирлинга первого рода задаются рекуррентным соотношением:
s (n, n) = 1, для n ≥ 0,
s (n,0) = 0, для n > 0,
 для 0 < k < n.
для 0 < k < n.
Доказательство.
Для n =1 это равенство проверяется непосредственно. Пусть перестановка (n -1)-го порядка распадается на k циклов. Число n можно добавить после любого числа в соответствующий цикл. Все полученные перестановки — различные и содержат k циклов, их количество (n -1)· s (n -1, k). Из любой перестановки (n -1)-го порядка, содержащей k -1 цикл, можно сформировать единственную перестановку n порядка, содержащую k циклов, добавив цикл образованный единственным числом n. Очевидно, что эта конструкция описывает все перестановки n -го порядка, содержащие k циклов. Тем самым равенство доказано.
Пример
Первые ряды:
| n\k
|
|
|
|
|
|
|
|
|
|
| | | | | | |
|
|
|
| | | | | |
|
|
| −1
|
| | | | |
|
|
|
| −3
|
| | | |
|
|
| −6
|
| −6
|
| | |
|
|
|
| −50
|
| −10
|
| |
|
|
| −120
|
| −225
|
| −15
|
|
| | | | | | | | |
В комбинаторике числом Стирлинга второго рода из n по k, обозначаемым  или
или  , называется количество неупорядоченных разбиений n -элементного множества на k непустых подмножеств.
, называется количество неупорядоченных разбиений n -элементного множества на k непустых подмножеств.
Рекуррентная формула
Числа Стирлинга второго рода удовлетворяют рекуррентному соотношению:
 , для n ≥ 0,
, для n ≥ 0,
 , для n > 0,
, для n > 0,
 для
для 
Явная формула

Пример
Начальные значения чисел Стирлинга второго рода приведены в таблице:
Свойства
Биективным отображением называется отображение, обладающее признаками инъективности и сюръективности одновременно.
Биекция
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 февраля 2012; проверки требуют 2 правки.


Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 февраля 2012; проверки требуют 2 правки.
Перейти к: навигация, поиск


Биективная функция.
Биекция — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением.
Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы.
Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества).
Определение
Функция  называется биекцией (и обозначается
называется биекцией (и обозначается  ), если она:
), если она:
- Переводит разные элементы множества
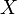 в разные элементы множества
в разные элементы множества  (инъективность). Иными словами,
(инъективность). Иными словами, -
 .
.
- Любой элемент из
 имеет свой прообраз (сюръективность). Иными словами,
имеет свой прообраз (сюръективность). Иными словами, -
 .
.
Примеры
- Тождественное отображение
 на множестве
на множестве 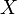 биективно.
биективно. -
 — биективные функции из
— биективные функции из  в себя. Вообще, любой моном одной переменнойнечетнойстепени является биекцией из
в себя. Вообще, любой моном одной переменнойнечетнойстепени является биекцией из  в себя.
в себя. -
 — биективная функция из
— биективная функция из  в
в  .
. -
 не является биективной функцией, если считать её определённой на всём
не является биективной функцией, если считать её определённой на всём  .
.
Свойства


Композиция инъекции и сюръекции, дающая биекцию.
- Функция
 является биективной тогда и только тогда, когда существует обратная функция
является биективной тогда и только тогда, когда существует обратная функция  такая, что
такая, что
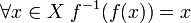 и
и 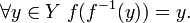
- Если функции
 и
и  биективны, то и композиция функций
биективны, то и композиция функций  биективна, в этом случае
биективна, в этом случае  . Коротко: композиция биекций является биекцией. Обратное, однако, неверно: если
. Коротко: композиция биекций является биекцией. Обратное, однако, неверно: если  биективна, то мы можем утверждать лишь, что
биективна, то мы можем утверждать лишь, что  инъективна, а
инъективна, а  сюръективна.
сюръективна.
Применения
В информатике
Организация связи «один к одному» между таблицамиреляционной БД на основе первичных ключей.
Числа Каталана
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
ЧислаКатала́на — числовая последовательность, встречающаяся во многих задачах комбинаторики. Последовательность названа в честь бельгийского математика Каталана, хотя была известна ещё Л. Эйлеру.
Первые несколько чисел Каталана:
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, … (последовательность A000108 в OEIS)
Определения
n -е число Каталана  можно определить одним из следующих способов:
можно определить одним из следующих способов:
- Количество разбиений выпуклого (n +2)-угольника на треугольники непересекающимися диагоналями.
- Количество правильных скобочных последовательностей длины 2 n, то есть таких последовательностей из n левых и n правых скобок, в которых количество открывающих скобок равно количеству закрывающих, и в любом её префиксе открывающих скобок не меньше, чем закрывающих.
Например, для n =3 существует 5 таких последовательностей:
((())), ()(()), ()()(), (())(), (()())
то есть 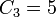 .
.
- Количество способов соединения 2 n точек на окружности n непересекающимися хордами.
- Количество неизоморфных упорядоченных бинарных деревьев с корнем и n +1 листьями.
Свойства
- Числа Каталана удовлетворяют рекуррентному соотношению:
 и
и  для
для 
Это соотношение легко получается из того, что любая непустая правильная скобочная последовательность однозначно представима в виде w =(w 1) w 2, где w 1, w 2 — правильные скобочные последовательности.
- Производящая функция чисел Каталана равна:

- Числа Каталана можно выразить через биномиальные коэффициенты:

Другими словами, число Каталана  равно разности центрального биномиального коэффициента и соседнего с ним в той же строке треугольника Паскаля.
равно разности центрального биномиального коэффициента и соседнего с ним в той же строке треугольника Паскаля.
- Асимптотически

Чтобы не ограничиваться одной только ссылкой, напишу приведенный в "Конкретной математике" вывод формулы для чисел Каталана. Красивое и очень простое рассуждение.
Определение (одно из многих). Числом Каталана Cn называется количество последовательностей длины (2n+1) a0, a1,..., a2n, составленных из +1 и -1, таких что сумма чисел равна +1, а все частичные суммы
a0, a0+a1,..., a0+...+a2n
положительны.
Лемма Рени. Если x1, x2,..., xm - любая последовательность целых чисел, сумма которых равна +1, то ровно у одного из её циклических сдвигов
x1, x2,..., xm
x2,..., xm, x1
xm, x1,..., xm-1
частичные суммы все положительны.
Доказательство. Продолжим последовательность периодически до бесконечной последовательности: xm+k=xk, для всех k>0. Если для этой бесконечной последовательности нарисовать график частичных сумм sn=x1+...+xn, то он будет иметь "средний наклон" 1/m, поскольку sn+m=sn+1. Весь график может быть заключён между двумя прямыми наклона 1/m. Эти прямые касаются графика ровно один раз на каждом периоде из m точек, поскольку прямые с наклоном 1/m могут проходить через точки с целыми координатами только один раз на m единиц. Единственная нижняя точка касания-- это то единственное место в цикле, начиная с которого все частные суммы будут положительны.
Подсчёт последовательностей из +1 и -1 с общей суммой +1.
Всего есть C2n+1n последовательностей, содержащих n элементов -1 и (n+1) элементов +1. Построим все C2n+1n последовательностей и все (2n+1) их циклических сдвигов в виде таблицы из C2n+1n строк и (2n+1) столбцов. Очевидно, что каждая последовательность встречается в таблице (2n+1) раз, по одному разу в каждом столбце. По лемме Рени в каждой строке содержится ровно одна последовательность с положительными частичными суммами. Таким образом, всего в таблице искомые последовательности встречается C2n+1n раз. Каждая встречается (2n+1) раз. Следовательно
Cn = C2n+1n/(2n+1) = C2nn/(n+1).
28) Биномиальный коэффициент
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
В математике биномиальные коэффициенты — это коэффициенты в разложениибинома Ньютона 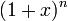 по степеням x. Коэффициент при
по степеням x. Коэффициент при  обозначается
обозначается  (иногда
(иногда  ) и читается «биномиальный коэффициент из n по k» (или «це из n по k»):
) и читается «биномиальный коэффициент из n по k» (или «це из n по k»):
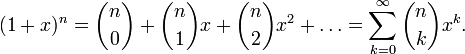
В комбинаторике биномиальный коэффициент  интерпретируется как количество сочетаний из n по k, то есть количество всех подмножеств (выборок) размера k в n -элементном множестве.
интерпретируется как количество сочетаний из n по k, то есть количество всех подмножеств (выборок) размера k в n -элементном множестве.
Биномиальные коэффициенты часто возникают в задачах комбинаторики и теории вероятностей. Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.
Явные формулы
Значение биномиального коэффициента  определено для всех целых чисел n и k. Явные формулы для вычисления биномиальных коэффициентов:
определено для всех целых чисел n и k. Явные формулы для вычисления биномиальных коэффициентов:
 для
для 
 для
для  или
или 
 для
для 
где  обозначает факториал числа m.
обозначает факториал числа m.
Треугольник Паскаля
Тождество

позволяет расположить биномиальные коэффициенты для неотрицательных целых чисел n, k в виде треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих:

Треугольная таблица, предложенная Паскалем в «Трактате об арифметическом треугольнике» (1654), отличается от выписанной здесь поворотом на 45°. Таблицы для изображения биномиальных коэффициентов были известны и ранее (Тарталье, О. Хайяму и др.).
Строки в треугольнике Паскаля в пределе стремятся к функции нормального распределения.
Если взять квадратную матрицу, отсчитав N элементов по катетам треугольника и повернув квадрат на любой из четырёх углов, то детерминант этих четырёх матриц по модулю равен 1 при любом N. Если поставить уголом из 1 в верхний левый угол, то детерминант матрицы будет равен 1.
В матрице  числа на диагонали i+j = const повторяют числа строк треугольника Паскаля. (i,j = 0...∞)
числа на диагонали i+j = const повторяют числа строк треугольника Паскаля. (i,j = 0...∞)
Матрицу  где i, j = 0…p можно разложить в произведение двух строго диагональных матриц. Первая нижнетреугольная, а вторая получается из первой путем транcпонирования. Элементы такой матрицы
где i, j = 0…p можно разложить в произведение двух строго диагональных матриц. Первая нижнетреугольная, а вторая получается из первой путем транcпонирования. Элементы такой матрицы 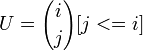
 где i,j = 0...p Далее обратная матрица к U
где i,j = 0...p Далее обратная матрица к U
 таким образом можно разложить обратную матрицу к
таким образом можно разложить обратную матрицу к  в произведение двух строго диагональных матриц и дать явное выражение для обратных элементов. Первая верхнетреугольная, а вторая получается из первой путем транспонирования.
в произведение двух строго диагональных матриц и дать явное выражение для обратных элементов. Первая верхнетреугольная, а вторая получается из первой путем транспонирования.
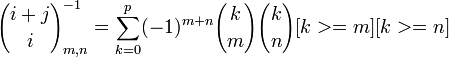 i,j,m,n = 0...p, если выражение в кваратных скобках ложно, то элемент суммы равен 0. Элементы обратной матрицы меняются при изменение её размера и в отличие от матрицы
i,j,m,n = 0...p, если выражение в кваратных скобках ложно, то элемент суммы равен 0. Элементы обратной матрицы меняются при изменение её размера и в отличие от матрицы  недостаточно приписать новую строку и столбец.
недостаточно приписать новую строку и столбец.
Свойства
Производящие функции
Для фиксированного значения n производящей функцией последовательности биномиальных коэффициентов  является:
является:
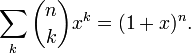
Для фиксированного значения k производящей функцией последовательности биномиальных коэффициентов  является:
является:
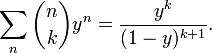
Двумерной производящей функцией биномиальных коэффициентов является:

Делимость
Из теоремы Люка следует, что:
-
 нечётен
нечётен  в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули.
в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули. -
 некратен простому p
некратен простому p  в p -ичной записи числа k все разряды не превосходят соответствующих разрядов числа n.
в p -ичной записи числа k все разряды не превосходят соответствующих разрядов числа n. - В последовательности биномиальных коэффициентов
 :
: - все числа не кратны заданному простому p

 , где натуральное число m < p;
, где натуральное число m < p; - все числа, кроме первого и последнего, кратны заданному простому p

 ;
; - количество нечётных чисел равно степени двойки (степень двойки равна количеству единиц в двоичной записи числа n);
- не может быть поровну чётных и нечётных чисел;
- количество не кратных простому p чисел равно
 , где числа
, где числа  — разряды p -ичной записи числа n; а число
— разряды p -ичной записи числа n; а число  — её длина.
— её длина.
Тождества
-

-
 (правило симметрии).
(правило симметрии). -

- Следствия тождества
 :
: -
 для
для  .
. -
 Это тождество можно усилить
Это тождество можно усилить -
 0<a<n
0<a<n -
 a>=n
a>=n -
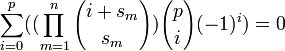 если
если  — более общий вид тождества выше.
— более общий вид тождества выше. -

-

-
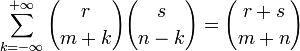 (свёртка Вандермонда).
(свёртка Вандермонда). -
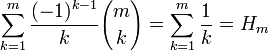 — m -оегармоническое число.
— m -оегармоническое число. - Мультисекция ряда
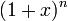 даёт тождество, выражающее сумму биномиальных коэффициентов с произвольным шагом s и смещением t
даёт тождество, выражающее сумму биномиальных коэффициентов с произвольным шагом s и смещением t  в виде замкнутой суммы из s слагаемых:
в виде замкнутой суммы из s слагаемых:

Асимптотика и оценки
где 
Алгоритмы вычисления
Биномиальные коэффициенты могут быть вычислены с помощью формулы  , если на каждом шаге хранить значения
, если на каждом шаге хранить значения  при
при  . Этот алгоритм особенно эффективен, если нужно получить все значения
. Этот алгоритм особенно эффективен, если нужно получить все значения  при фиксированном
при фиксированном  . Алгоритм требует
. Алгоритм требует  памяти (
памяти (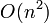 при вычислении всей таблицы биномиальных коэффициентов) и
при вычислении всей таблицы биномиальных коэффициентов) и 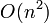 времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени).
времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени).
При фиксированном значении k биномиальные коэффициенты могут быть вычислены по рекуррентной формуле  с начальным значением
с начальным значением 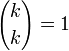 . Для вычисления значения
. Для вычисления значения  этот метод требует
этот метод требует  памяти и
памяти и  времени.
времени.
Задача о покрытии
Найти такие множества Ti, i = 1, 2, …, r, чтобы  (чтобы объединение этих множеств «покрыло» S). Например, застелить весь пол в комнате несколькими коврами. Ковры могут накладываться друг на друга (множества могут пересекаться), но незакрытых участков поФла быть не должно.
(чтобы объединение этих множеств «покрыло» S). Например, застелить весь пол в комнате несколькими коврами. Ковры могут накладываться друг на друга (множества могут пересекаться), но незакрытых участков поФла быть не должно.
Во многих задачах покрытие должно быть наиболее экономичным (так называемое минимальное покрытие), когда



 (чтобы объединение этих множеств «покрыло» S). Например, застелить весь пол в комнате несколькими коврами. Ковры могут накладываться друг на друга (множества могут пересекаться), но незакрытых участков поФла быть не должно.
(чтобы объединение этих множеств «покрыло» S). Например, застелить весь пол в комнате несколькими коврами. Ковры могут накладываться друг на друга (множества могут пересекаться), но незакрытых участков поФла быть не должно. (чтобы объединение этих множеств вошло в S).
(чтобы объединение этих множеств вошло в S). (чтобы объединение этих непересекающихся множеств дало S).
(чтобы объединение этих непересекающихся множеств дало S).



 .
. способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно
способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно  .
. способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах –
способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах –  .
. . Число перестановок, где на своих местах стоят хотя бы r элементов –
. Число перестановок, где на своих местах стоят хотя бы r элементов –  . Число перестановок, где все элементы стоят на своих местах
. Число перестановок, где все элементы стоят на своих местах  . Подставляем в формулу решета:
. Подставляем в формулу решета: 
 ,
, .
.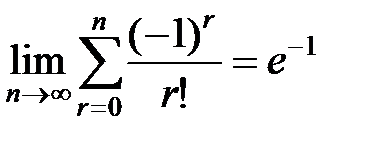 , то
, то  .
. , где pi – все простые делители n. (
, где pi – все простые делители n. ( - произведение по всем простым делителям числа n).
- произведение по всем простым делителям числа n). (так как pi делят n нацело).
(так как pi делят n нацело).
 . #
. # .
.
 .
.
 .
. .
. из множества переменных в множество термов. Для обозначения действия подстановки, как правило, используют постфиксную нотацию. Например,
из множества переменных в множество термов. Для обозначения действия подстановки, как правило, используют постфиксную нотацию. Например,  означает результат действия подстановки
означает результат действия подстановки  на терм
на терм  .
. было конечным. В таком случае её можно задать простым перечислением пар «переменная-значение». Поскольку каждую такую подстановку можно свести к последовательности подстановок, замещающих всего по одной переменной каждая, не ограничивая общности можно считать, что подстановка задаётся одной парой «переменная-значение», что обычно и делается.
было конечным. В таком случае её можно задать простым перечислением пар «переменная-значение». Поскольку каждую такую подстановку можно свести к последовательности подстановок, замещающих всего по одной переменной каждая, не ограничивая общности можно считать, что подстановка задаётся одной парой «переменная-значение», что обычно и делается. ,
,  и произвольной переменной
и произвольной переменной  результат замещения произвольного свободного вхождения
результат замещения произвольного свободного вхождения  : объект
: объект  ;
; : объект
: объект  . Тогда
. Тогда  для произвольных атомарных
для произвольных атомарных  ;
; : объект
: объект  . Тогда
. Тогда  ;
; : объект
: объект  . Тогда [
. Тогда [  ;
; : объект
: объект  -абстракцией
-абстракцией  , причем
, причем  . Тогда:
. Тогда: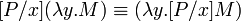 для
для  или
или 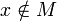 ;
; для
для 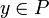 и
и 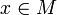 .
.

 для 0 < k < n.
для 0 < k < n. или
или  , называется количество неупорядоченных разбиений n -элементного множества на k непустых подмножеств.
, называется количество неупорядоченных разбиений n -элементного множества на k непустых подмножеств. , для n ≥ 0,
, для n ≥ 0, , для n > 0,
, для n > 0, для
для 

 где
где 

 — число Белла.
— число Белла.



 называется биекцией (и обозначается
называется биекцией (и обозначается  ), если она:
), если она: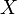 в разные элементы множества
в разные элементы множества  (инъективность). Иными словами,
(инъективность). Иными словами,  .
. .
. на множестве
на множестве  — биективные функции из
— биективные функции из  в себя. Вообще, любой моном одной переменнойнечетнойстепени является биекцией из
в себя. Вообще, любой моном одной переменнойнечетнойстепени является биекцией из  — биективная функция из
— биективная функция из  .
. не является биективной функцией, если считать её определённой на всём
не является биективной функцией, если считать её определённой на всём 
 такая, что
такая, что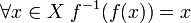 и
и 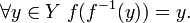
 и
и  биективны, то и композиция функций
биективны, то и композиция функций  биективна, в этом случае
биективна, в этом случае  . Коротко: композиция биекций является биекцией. Обратное, однако, неверно: если
. Коротко: композиция биекций является биекцией. Обратное, однако, неверно: если  можно определить одним из следующих способов:
можно определить одним из следующих способов: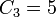 .
. и
и  для
для 



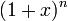 по степеням x. Коэффициент при
по степеням x. Коэффициент при  обозначается
обозначается  (иногда
(иногда  ) и читается «биномиальный коэффициент из n по k» (или «це из n по k»):
) и читается «биномиальный коэффициент из n по k» (или «це из n по k»):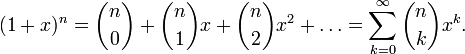
 для
для 
 для
для  или
или 
 для
для 
 обозначает факториал числа m.
обозначает факториал числа m.

 числа на диагонали i+j = const повторяют числа строк треугольника Паскаля. (i,j = 0...∞)
числа на диагонали i+j = const повторяют числа строк треугольника Паскаля. (i,j = 0...∞)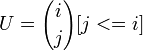
 где i,j = 0...p Далее обратная матрица к U
где i,j = 0...p Далее обратная матрица к U таким образом можно разложить обратную матрицу к
таким образом можно разложить обратную матрицу к 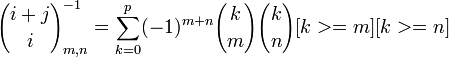 i,j,m,n = 0...p, если выражение в кваратных скобках ложно, то элемент суммы равен 0. Элементы обратной матрицы меняются при изменение её размера и в отличие от матрицы
i,j,m,n = 0...p, если выражение в кваратных скобках ложно, то элемент суммы равен 0. Элементы обратной матрицы меняются при изменение её размера и в отличие от матрицы  является:
является: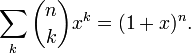
 является:
является: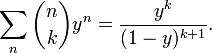

 в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули.
в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули. :
:  , где натуральное число m < p;
, где натуральное число m < p; ;
; , где числа
, где числа  — разряды p -ичной записи числа n; а число
— разряды p -ичной записи числа n; а число  — её длина.
— её длина.
 (правило симметрии).
(правило симметрии).
 :
: 

 для
для  .
. Это тождество можно усилить
Это тождество можно усилить 0<a<n
0<a<n a>=n
a>=n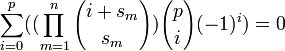 если
если  — более общий вид тождества выше.
— более общий вид тождества выше.

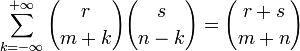 (свёртка Вандермонда).
(свёртка Вандермонда).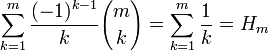 — m -оегармоническое число.
— m -оегармоническое число. в виде замкнутой суммы из s слагаемых:
в виде замкнутой суммы из s слагаемых:

 при
при 
 , при
, при 


 , если на каждом шаге хранить значения
, если на каждом шаге хранить значения  при
при  . Этот алгоритм особенно эффективен, если нужно получить все значения
. Этот алгоритм особенно эффективен, если нужно получить все значения  . Алгоритм требует
. Алгоритм требует  памяти (
памяти (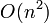 при вычислении всей таблицы биномиальных коэффициентов) и
при вычислении всей таблицы биномиальных коэффициентов) и  с начальным значением
с начальным значением 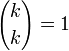 . Для вычисления значения
. Для вычисления значения  памяти и
памяти и 

