Число r -сочетаний с повторениями из n -множества равно
 .
.
– доказательство с помощью рекуррентной формулы.
Метод базируется на получении формулы, позволяющей вычислять значения искомой величины шаг за шагом, исходя из известных начальных значений и значений, вычисленных на предыдущих шагах.
Рекуррентная формула r -го порядка – формула вида
an = f (n, an- 1, an- 2, …, an-r).
Формула выражает при n>r каждый член последовательности { ai } через предыдущие r членов. Построение рекуррентной формулы состоит из следующих шагов.
1. Выработка начальных условий исходя из каких-либо очевидных соотношений.
Обозначим  через f (n,r). Очевидно, что
через f (n,r). Очевидно, что
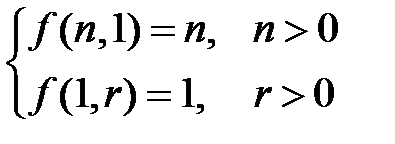 (1)
(1)
2. Логические рассуждения. Зафиксируем какой-либо элемент во множестве S. Тогда относительно любого r -сочетания с повторениями из n -множества S можно сказать, содержит ли оно данный зафиксированный элемент или нет.
Если содержит, то остальные (r -1) элемент можно выбрать f (n, r -1) способами.
Если не содержит (в выборке этого элемента нет), то r -сочетание составлено из элементов (n -1)-множества (множество S за исключением данного зафиксированного элемента). Число таких сочетаний f (n -1, r).
Т.к. эти случаи взаимоисключающие, то по правилу суммы
 (2)
(2)
3. Проверка формулы на некоторых значениях и вывод общей закономерности.
1) Вычислим f (n,0). Из (2) следует
 . (3)
. (3)
Тогда f (n,0)= f (n,1)- f (n -1,1). Из (1) f (n,1)= n, f (n -1,1)= n -1.
Следовательно, f (n,0)= n -(n -1)=1=  .
.
2) f (n,1) = f (n,0)+ f (n -1,1) = 1+ n- 1 = n =  =
=  .
.
3) f (n,2) = f (n,1)+ f (n -1,2) = n + f (n -1,1)+ f (n -2,2) = n +(n -1)+ f (n -2,1)+ f (n -3,2) = … =
= n +(n -1)+…+2+1 = 
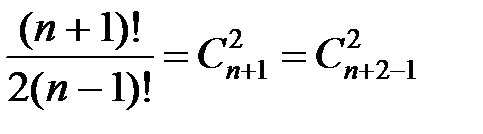 .
.
(сумма арифметической прогрессии)
4) f (n,3) = f (n,2)+ f (n -1,3) =  + f (n -1,2)+ f (n -2,3) =
+ f (n -1,2)+ f (n -2,3) =  +
+  + f (n -2,2)+ f (n -3,3) = … =
+ f (n -2,2)+ f (n -3,3) = … =
 .
.
(сумма геометрической прогрессии)
5) f (n,4) = 
На основе частных случаев можно предположить, что

Проверка начальных условий с помощью полученной формулы.
 ,
,
что согласуется с (1) #
19, 20) Число бинарных деревьев с n вершинами равно C(n), где C(n) – это n-ое число Каталана.
Количество бинарных деревьев из n вершин называется числом Каталана, которое обладает множеством интересных свойств. N-ое число Каталана считается по формуле (2n)! / (n+1)!n!, которая растёт экспоненциально. (В Википедии предложено несколько доказательств, что это форма числа Каталана.) Число бинарных деревьев данного размера
0 1
1 1
2 2
4 14
8 1430
12 208012
16 35357670
Подстановка
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Это статья о подстановке как о синтаксической операции над термами. Возможно, вас интересует перестановка.
В математике и компьютерных науках подстановка — это операция синтаксической замены подтермов данного терма другими термами, согласно определённым правилам. Обычно речь идёт о подстановке терма вместо переменной.
Содержание
- 1 Определения и обозначения
- 2 Подстановка переменной в λ-исчислении
- 3 Подстановка переменной в программировании
- 4 См. также
- 5 Ссылки
|
Определения и обозначения
Для подстановки не существует универсальной, согласованной нотации, равно как и стандартного определения. Понятие подстановки варьируется не только в рамках разделов, но и на уровне отдельных публикаций. В целом, можно выделить контекстную подстановку и подстановку «вместо». В первом случае место в терме, где происходит замена, задаётся контекстом, то есть частью терма, «окружающим» это место. В частности, такое понятие подстановки используется в переписывании. Второй вариант более распространён. В этом случае подстановка обычно задаётся некоторой функцией  из множества переменных в множество термов. Для обозначения действия подстановки, как правило, используют постфиксную нотацию. Например,
из множества переменных в множество термов. Для обозначения действия подстановки, как правило, используют постфиксную нотацию. Например,  означает результат действия подстановки
означает результат действия подстановки  на терм
на терм  .
.
В подавляющем большинстве случаев требуется чтобы подстановка имела конечный носитель, то есть, чтобы множество  было конечным. В таком случае её можно задать простым перечислением пар «переменная-значение». Поскольку каждую такую подстановку можно свести к последовательности подстановок, замещающих всего по одной переменной каждая, не ограничивая общности можно считать, что подстановка задаётся одной парой «переменная-значение», что обычно и делается.
было конечным. В таком случае её можно задать простым перечислением пар «переменная-значение». Поскольку каждую такую подстановку можно свести к последовательности подстановок, замещающих всего по одной переменной каждая, не ограничивая общности можно считать, что подстановка задаётся одной парой «переменная-значение», что обычно и делается.
Последнее определение подстановки является, видимо, самым типичным и часто используемым. Однако и для него не существует единой общепринятой нотации. Наиболее часто для обозначения подстановки a вместо x в t используется запись t [ a / x ], t [ x:= a ] или t [ x ← a ].
Подстановка переменной в λ-исчислении
В λ-исчислении, подстановка определяется структурной индукцией. Для произвольных объектов  ,
,  и произвольной переменной
и произвольной переменной  результат замещения произвольного свободного вхождения
результат замещения произвольного свободного вхождения  в
в  считается подстановкой и определяется индукцией по построению
считается подстановкой и определяется индукцией по построению  :
:
(i) базис:  : объект
: объект  совпадает с переменной
совпадает с переменной  . Тогда
. Тогда  ;
;
(ii) базис:  : объект
: объект  совпадает с константой
совпадает с константой  . Тогда
. Тогда  для произвольных атомарных
для произвольных атомарных  ;
;
(iii) шаг:  : объект
: объект  неатомарный и имеет вид аппликации
неатомарный и имеет вид аппликации  . Тогда
. Тогда  ;
;
(iv) шаг:  : объект
: объект  неатомарный и является
неатомарный и является  -абстракцией
-абстракцией  . Тогда [
. Тогда [  ;
;
(v) шаг:  : объект
: объект  неатомарный и является
неатомарный и является  -абстракцией
-абстракцией  , причем
, причем  . Тогда:
. Тогда:
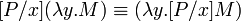 для
для  и
и  или
или 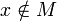 ;
;
 для
для  и
и 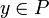 и
и 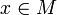 .
.



 .
. через f (n,r). Очевидно, что
через f (n,r). Очевидно, что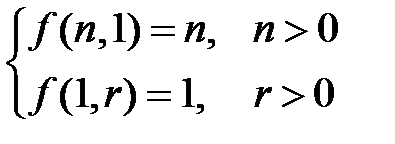 (1)
(1) (2)
(2) . (3)
. (3) .
. =
=  .
.
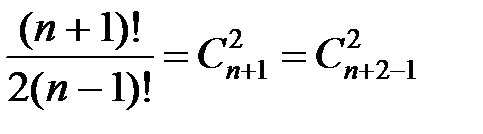 .
. + f (n -1,2)+ f (n -2,3) =
+ f (n -1,2)+ f (n -2,3) =  +
+  + f (n -2,2)+ f (n -3,3) = … =
+ f (n -2,2)+ f (n -3,3) = … = .
.

 ,
, из множества переменных в множество термов. Для обозначения действия подстановки, как правило, используют постфиксную нотацию. Например,
из множества переменных в множество термов. Для обозначения действия подстановки, как правило, используют постфиксную нотацию. Например,  означает результат действия подстановки
означает результат действия подстановки  на терм
на терм  .
. было конечным. В таком случае её можно задать простым перечислением пар «переменная-значение». Поскольку каждую такую подстановку можно свести к последовательности подстановок, замещающих всего по одной переменной каждая, не ограничивая общности можно считать, что подстановка задаётся одной парой «переменная-значение», что обычно и делается.
было конечным. В таком случае её можно задать простым перечислением пар «переменная-значение». Поскольку каждую такую подстановку можно свести к последовательности подстановок, замещающих всего по одной переменной каждая, не ограничивая общности можно считать, что подстановка задаётся одной парой «переменная-значение», что обычно и делается. ,
,  и произвольной переменной
и произвольной переменной  результат замещения произвольного свободного вхождения
результат замещения произвольного свободного вхождения  : объект
: объект  ;
; : объект
: объект  . Тогда
. Тогда  для произвольных атомарных
для произвольных атомарных  ;
; : объект
: объект  . Тогда
. Тогда  ;
; : объект
: объект  . Тогда [
. Тогда [  ;
; : объект
: объект  -абстракцией
-абстракцией  , причем
, причем  . Тогда:
. Тогда: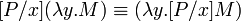 для
для  или
или 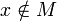 ;
; для
для 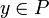 и
и 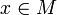 .
.


