Алгоритм метода главных компонент

1. Найти матрицу нормированных показателей Z.

2. Определить ковариационную матрицу для Z – она же будет корреляци-

онной матрицей R исходных показателей X.

3. Вычислить для матрицы R собственные значения

λ i,

i =1,..., p, и найти

соответствующие собственные векторы-строки

a (i)

– коэффициенты ли-

нейных комбинаций исходных признаков – главных компонент

Fi.

4. Найти матрицу A: строками матрицы A являются найденные собствен-

ные векторы

a (i).

5. Найти матрицу значений главных компонент:

F = A ⋅ Z.

6. Выделить несколько основных первых компонент, например, по правилу

Кайзера: значимы те главные компоненты, для которых

λ i >1.

 

Пример 13.1. В таблице представлены данные трёх показателей на пя-

ти различных объектах.

 

№
X 1
X 2
X 3	-1	-1

а) Определите долю общей дисперсии, которую объясняет первая главная компонента, и проранжируйте объекты по первой главной компоненте. б) Определите долю общей дисперсии, которую объясняют первые две глав- ные компоненты, и изобразите исследуемые объекты точками в пространстве двух главных компонент.

Решение. По данным определяем выборочные средние:

X 1 = 3,8;

X 2 =11;

X 3 = 0,2

и средние квадратические отклонения:

s 1 = 0,84;

s 1 =1;

s 1 =1,3. После этого получим матрицу нормированных показателей Z и

корреляционную матрицу R:

⎛− 0,96

⎜

 

0,24

−0,96

 

0,24

1,43 ⎞

⎟

⎛ 1 0,3

⎜

0,5 ⎞

⎟

Z = ⎜ 1

⎜

−1 −1

0 1 ⎟,

⎟

R = ⎜0,3 1

⎜

0,19 ⎟.

⎟

⎝− 0,92

− 0,92

− 0,15

1,38

0,61⎠

⎝0,5

0,19 1 ⎠

Для отыскания собственных чисел матрицы R составим характеристиче-

ское уравнение: | R − λ E | = 0, которое после преобразований примет вид:

λ3 −3λ2 + 2,62λ−0,68 = 0.

Корни этого уравнения – собственные числа матрицы R:

λ1 =1,68;

λ2 = 0,84;

λ3 = 0,48. Заметим, что

λ1 + λ2 + λ3 = 3, следовательно, первая

главная компонента объясняет

λ1 / 3 = 0,56

общей дисперсии, а первые две

компоненты –

(λ1 + λ2) / 3 = 0,84

общей дисперсии.

Теперь для каждого собственного числа найдём соответствующий ему собственный вектор. Для этого нужно решить неопределённые системы

i

уравнений

(R − λ E) ⋅ a (i) = 0.

В результате получим следующие (нормированные) собственные векторы:

a (1) = (0,65; 0,46; 0,61),

a (2) = (0,18; − 0,87; 0,46),

a (3) = (−0,74; 0,19; 0,65).

Таким образом, получаем главные компоненты:

F 1 = 0,65 X 1 + 0,46 X 2 + 0,61 X 3,

F 2 = 0,18 X 1 −0,87 X 2 + 0,46 X 3,

F 3 = −0,74 X 1 + 0,19 X 2 + 0,65 X 3

и матрицу

⎛

⎜

A = ⎜

⎜

 

 

0,65

0,18

 

 

0,46

−0,87

0,61⎞

⎟

0,46 ⎟.

⎟

⎝− 0,74

0,19

0,65 ⎠

Найдём теперь матрицу значений главных компонент:

⎛ 0,24

⎜

0,65

−0,69

−0,87

0,66 ⎞

⎟

⎜

F = A ⋅ Z = ⎜ −1,48

⎝− 0,72

0,81

−0,91

0,41

−1,14

0,37

1,04

−0,1⎟.

⎠

1,73 ⎟

Если, например, упорядочить объекты в порядке убывания значений первой главной компоненты, то получим такую последовательность объек- тов: (5), (2), (1), (3), (4).

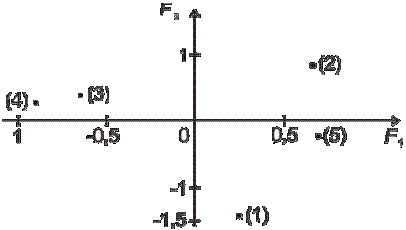Для предварительной (наглядной) классификации объектов изобразим их точками в пространстве первых двух компонент (рис. 13.2).

 

Рис. 13.2

Судя по полученному изображению объектов в пространстве первых двух компонент, объекты (3) и (4) нужно относить к одной группе, а остальные объекты – к другой, при этом, вероятно, целесообразно их также разделить на две группы: (1) и (2), (5).

 

Факторный анализ

Факторный анализ возник в 1904 году в задачах психологии. Сегодня область его приложения значительно шире – он находит применение при ре- шении различных задач экономики, медицины, биологии т.д. Большой вклад в развитие факторного анализа внесли Ч. Спирмэн, Р. Кеттел18.

 

Задача факторного анализа состоит в следующем. Пусть

T

X = (X 1,..., Xp)

– p -мерный вектор наблюдаемых показателей, связанный

с каждым из n изучаемых объектов. Требуется при заданном q (которое,

как правило, значительно меньше p) определить такой вектор скрытых

 

факторов

F = (F,..., F) T

 

и матрицу нагрузок A, имеющую размерность

)

1 q

p

p × q, что

X = A ⋅ F + ε,

где

ε= (ε1

,..., ε T

– вектор попарно независимых остаточных факторов.

При этом среди всех таких линейных комбинаций изменчивость координат F должна наилучшим образом (в некотором смысле) объяснять изменчи- вость исходных показателей X.

Экономический смысл новых показателей

F 1,..., Fq

состоит в том, что

они позволяют выявить некоторые объективно существующие скрытые факторы, оказывающие влияние на измеряемые показатели.

Если остаточные факторы

ε1,..., ε p

невелики, то компонентный и фак-

торный анализы должны давать близкие результаты.

Замечание. Задача факторного анализа не всегда разрешима. Принци- пиальная возможность нахождения скрытых факторов связана в основном с высокой коррелированностью исходных признаков. Тогда скрытые факто- ры – те причины, которые объясняют эту коррелированность.

 

Замечание. Если задача факторного анализа разрешима, то существует бесконечно много решений, а именно для произвольной обратимой матрицы C будет справедливо равенство:

X = (A ⋅ C) ⋅(C −1 ⋅ F) + ε.

 

Обычно в качестве матрицы C берут ортогональную матрицу. Поскольку умножение на ортогональную матрицу соответствует повороту, то решение принципиально может быть определено с точностью до поворота. Это об-

 

18 Рэймонд Бернард Кеттел (1905 – 1998) – британский и американский психолог.

стоятельство имеет и положительную сторону: путем поворота можно изме- нить содержание факторов без снижения качества решения и тем самым дать им качественную интерпретацию.

T

При наложении на искомые факторы условий нормировки ковариацион-

ную матрицу S показателей

X = (X

1,..., Xp

можно представить в виде:

)

S = A ⋅ AT + V,

где V – ковариационная матрица остаточных факторов ε, которая в силу не-

зависимости ε i

и ε j

(i ≠

j) является диагональной. Возможность такого пред-

ставления равносильна возможности решения задачи факторного анализа.

Для нахождения матрицы факторных нагрузок A используют различ- ные методы: метод главных факторов, метод максимального правдоподо- бия, групповой метод, метод минимальных остатков и др. Рассмотрим ме- тод главных факторов, предложенный Г. Томсоном19.

 

Алгоритм факторного анализа (метод главных факторов)

1. Найти матрицу нормированных показателей Z.

2. Определить ковариационную матрицу для Z – она же будет корреляци-

онной матрицей R исходных показателей X.

3. Определить редуцированную матрицу

Rh, в которой в отличие от матрицы

i

R на главной диагонали стоят общности

h 2 <1, а не единицы. Таким обра-

зом, коррелированность исходных признаков

X 1,..., Xp

может быть объяс-

нена не полностью, а несколько меньше с учетом остаточных факторов ε.

Имеется несколько простых методов нахождения общностей: метод наи-

h

i

большей корреляции – в качестве общности

2 (i =1,..., p) берут наиболь-

ший по модулю коэффициент корреляции в i -й строке; метод средней кор-

h

i

реляции – в качестве

2 берут арифметическое среднее модулей коэффици-

2 r ⋅ r

ентов корреляции в j -й строке; метод триад – hi

= ik il, где

rkl

rik

и ril –

два наибольших по модулю коэффициента корреляции в i -й строке.

4. Вычислить для редуцированной матрицы

Rh собственные значения

λ i,

i =1,..., p:

λ1 > λ2 >... > λ p. Найти соответствующие собственные векто-

 

ры-столбцы

a (i).

5. Из найденных собственных значений

λ i,

i =1,..., p, выбрать первые q,

объясняющие наибольшую долю корреляций исходных признаков.

6. Найти матрицу факторных нагрузок A: столбцами матрицы A являются

i

векторы

λ⋅ a (i).

7. Оценить влияние остаточных факторов: V

= R − AAT.

 

19 Годфри Хилтон Томсон (1881 – 1955) – английский педагог и психолог.

8. Найти численные значения скрытых факторов для каждого из наблюдае-

мых объектов (обычно пользуются методом Бартлетта20):

F = (AT ⋅ V −1 ⋅ A)−1⋅ AT ⋅ V −1 ⋅ X.

9. Проверить на уровне значимости αгипотезу о том, что число скрытых

факторов равно q. Для этого сравнить наблюдаемое значение статистики

T

 

χ =

(n

2

набл.

−1)

⋅ln det (AA)

det R

с критическим χ2

= χ2 (α, ((p − q) 2 − p − q)/ 2). Если χ2

> χ2

 

, то гипотезу

кр.

следует отвергнуть; если же χ2

< χ2

 

, то – принять.

набл. кр.

набл. кр.

 

Пример 13.2. По данным примера 13.1 определите два скрытых фактора.

Решение. Проведём нормировку исходных показателей, тем самым перейдём от ковариационной матрицы S к корреляционной матрице R:

⎛ 1 0,3

⎜

0,5 ⎞

⎟

R = ⎜0,3 1

⎜

0,19⎟.

⎟

⎝0,5

0,19 1 ⎠

Для определения общностей и нахождения редуцированной матрицы вос-

пользуемся методом наибольшей корреляции. Тогда общности

h 2 = 0,5,

h 2 = 0,3,

h 2 = 0,5, а редуцированная матрица:

⎛0,5

⎜

⎜

Rh = ⎜0,3

⎝0,5

0,3

0,3

0,19

0,5 ⎞

⎟

⎠

0,19⎟.

0,5 ⎟

Находим первые два собственных числа матрицы

Rh:

λ1 =1,15;

λ2 = 0,18,

и соответствующие им собственные векторы:

a (2) = (0,01; − 0,86; 0,51).

Таким образом, матрица факторных нагрузок:

a (1) = (0,67; 0,38; 0,64),

⎛0,72 0 ⎞

⎜ ⎟

A = ⎜0,41

⎜

− 0,36⎟,

⎟

следовательно,

⎝0,69

0,22 ⎠

⎛0,48 0 0 ⎞

⎜ ⎟

V = ⎜ 0

⎜

0,7

0 ⎟.

⎟

⎝ 0 0

0,48⎠

 

 

20 Морис Стивенсон Бартлетт ( 1910 – 2002) – английский статистик.

Теоретические вопросы и задания

1. С какой целью используют компонентный анализ при статистической обработке данных? В чем его суть?

2. Сформулируйте алгоритм поиска главных компонент.

3. Что является основной задачей факторного анализа? Каков его общий ал-

горитм?

4. Какие дополнительные условия обычно накладывают на матрицу фактор-

ных нагрузок?

5. Как найти значения скрытых факторов для наблюдаемых объектов?

 

Задачи и упражнения

1. Хозяйственную деятельность предприятий можно охарактеризовать тремя

показателями:

X 1 – трудоемкость единицы продукции,

X 2 – коэффициент

сменности оборудования,

X 3 – удельный вес покупных изделий. Для

10 предприятий города эти показатели следующие:

 

№
X 1	0,38	0,24	0,31	0,42	0,51	0,31	0,37	0,16	0,18	0,43
X 2	1,40	1,20	1,15	1,09	5,00	1,36	1,15	1,87	2,17	1,61
X 3	0,30	0,56	0,42	0,26	0,16	0,45	0,31	0,08	0,63	0,03

а) Определите долю общей дисперсии, которую объясняет первая главная компонента, и проранжируйте предприятия по первой главной компонен- те. б) Изобразите предприятия точками в пространстве двух первых ком- понент. Сделайте экономические выводы.

2. По данным задачи 1 определите: а) один скрытый фактор и проверьте ги- потезу, что скрытый фактор один; б) два скрытых фактора и проверьте гипотезу, что скрытых факторов два. Найдите численные значения факто- ров методом Бартлетта.

 

Домашнее задание

1. В таблице представлены данные о финансовой активности восьми фирм:

X 1 – коэффициент рентабельности,

X 2 – коэффициент оборачиваемости,

X 3 – коэффициент ликвидности,

X 4 – коэффициент структуры капитала.

 

№
X 1	1,68	1,34	1,34	1,42	1,36	1,52	1,55	1,31
X 2	0,46	0,70	0,45	0,59	0,85	0,59	0,60	0,62
X 3	1,31	1,46	1,32	1,28	1,42	1,28	1,26	1,14
X 4	0,55	0,60	0,57	0,63	0,78	0,75	0,64	0,59

Определите долю общей дисперсии, которую объясняют первые две глав- ные компоненты, и изобразите предприятия в пространстве этих компо- нент. Сделайте экономические выводы.

2. По данным задачи 1 определите два скрытых фактора и проверьте гипоте- зу, что скрытых факторов два. Найдите численные значения факторов ме- тодом Бартлетта.

 

 

Занятие 14. Классификация с обучением.

Дискриминантный анализ

 

При проведении статистических исследований часто возникает необхо- димость разделить неоднородную совокупность по однородным (в некотором смысле) группам (классам). Такое расчленение в дальнейшем дает лучшие результаты моделирования зависимостей между отдельными признаками.

Разработка методов решения таких задач в случае, когда исследователь обладает так называемыми обучающими выборками (классификация с обу- чением), является содержанием дискриминантного анализа, основы которого были заложены Р. Фишером в 1936 году.

Пусть имеется множество объектов наблюдения (генеральная совокуп-

ность), каждый из которых характеризуется несколькими признаками (пере-

менными):

xij

– значение j -го признака у i -го объекта. Предположим, что

всё множество объектов разбито на k (k ≥ 2) подмножеств (классов). Из ка-

ждого подмножества взята выборка объёмом

ni, где i – номер класса

(i =1,

2, K,

k).

Определение 14.1. Признаки, которые используются для того, что- бы отличить один класс от другого, называются дискриминантными пе- ременными.

Дадим геометрическую интерпретацию дискриминантного анализа в

случае, когда каждый объект характеризуется двумя признаками

X 1 и

X 2.

 

 

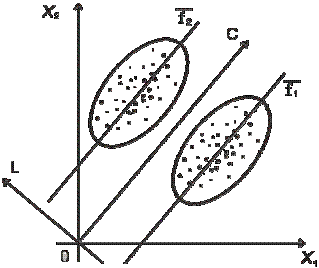Рис. 14.1

 

 

На рисунке 14.1 точками изображены объекты, принадлежащие двум различным группам. Если рассмотреть проекции объектов (точек) на каждую ось, то множества проекций, вообще говоря, могут пересекаться, т.е. иметь одинаковые характеристики.

Чтобы наилучшим образом разделить эти две группы, нужно построить

некоторую линейную комбинацию признаков

X 1 и

X 2, т.е. определить но-

вую систему координат

(L, C), причем так, чтобы множества проекций на

ось L объектов, принадлежащих разным группам, были максимально разде- лены; ось С, перпендикулярная к оси L, должна при этом разделять два «об- лака» точек: группы должны быть расположены по разные стороны от оси С. Это означает, что должны быть определены коэффициенты прямой

C = f (x) = a 1 x 1 + a 2 x 2, называемой канонической дискриминантной функцией.

Замечание. Наиболее важный случай, когда дискриминантная функ-

ция является линейной, хотя иногда рассматривают и другие виды функций.

 

Обозначим

 

xij

 

– среднее значение j -го признака для i -го класса. Тогда

для каждого из двух классов средние значения функции

f (x)

будут равны

f 1 (x) = a 1 x 11 + a 2 x 12 и

f 2 (x) = a 1 x 21 + a 2 x 22. Геометрически эти равенства оп-

ределяют две прямые, проходящие через центры классов, перпендикулярные оси L (см. рис. 14.1). Тогда в качестве дискриминантной функции можно

взять функцию

C = a 1 x 1 + a 2 x 2, находящуюся на одинаковых расстояниях от

первой и второй прямой.

Пусть имеются две обучающие выборки, сделанные из p -мерных нор- мальных генеральных совокупностей с неизвестными, но равными ковариа- ционными матрицами. Множество объектов, характеризующих эти классы,

может быть записано в виде двух матриц:

⎛ x 11

⎜

x 12

L x 1 p ⎞

⎟

⎛ y 11

⎜

⎜

y 12

L y 1 p ⎞

⎟

⎜ x 21

X = ⎜

x 22

L x 2 p ⎟

⎝

⎟,

Y = ⎜

y 21

y 22

L y 2 p ⎟

y

⎟.

⎟

⎜ L L L L⎟

⎜ L L L L⎟

x

⎜

⎝ n 11

xn 1 2

L xn 1 p ⎠

⎜ yn 1

yn 2 2 L

⎟

n

2 p ⎠

Также дана матрица новых наблюдений:

⎛ z 11

⎜

⎜ z 21

Z = ⎜

⎜ L

z 12

z 22

L

L z 1 p ⎞

⎟

L z 2 p ⎟

L

⎟.

⎟

L ⎟

z

⎜

⎝ m 1

zm 2

L zmp ⎠

Целью дискриминантного анализа является отношение нового наблюде-

ния (строки матрицы Z) либо к классу X, либо к классу Y.