Многие задачи естествознания и техники получили решение благодаря одному из основных понятий математического анализа - определенному интегралу. Нахождение площадей, ограниченных кривыми, длин дуг, объемов, работы, пути, скорости, моментов инерции и т. д., сводится к его вычислению. Рассмотрим задачи, приводящие к понятию определенного интеграла.
Задача о массе прямолинейного стержня. Дан тонкий стержень длины  , его масса распределена неравномерно с плотностью
, его масса распределена неравномерно с плотностью  . Найти массу всего стержня.
. Найти массу всего стержня.
Решение. Разберем условие задачи. Под тонким стержнем мы будем понимать отрезок прямой, ограниченный точками 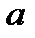 и
и  числовой оси
числовой оси  . Плотность вещества стержня в данной точке есть предел средней плотности
. Плотность вещества стержня в данной точке есть предел средней плотности  , где
, где 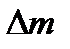 - масса отрезка
- масса отрезка  , при стремлении
, при стремлении  к нулю.
к нулю.
Требуется найти массу стержня.
Решение
Так как плотность распределена неравномерно, то для наиболее точного ее нахождения разобьем весь стержень точками на  достаточно малых частей (см. рис.)
достаточно малых частей (см. рис.)
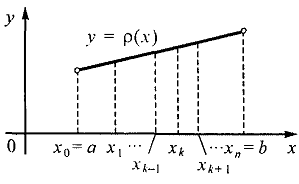 Обозначим длину отрезка
Обозначим длину отрезка  через
через  . В силу того, что длины отрезков малы, в границах каждого из них плотность стержня можно считать постоянной и равной
. В силу того, что длины отрезков малы, в границах каждого из них плотность стержня можно считать постоянной и равной  , где
, где  - одна из точек k-го отрезка
- одна из точек k-го отрезка  . Тогда масса этого отрезка стержня равна
. Тогда масса этого отрезка стержня равна  . Масса всего стержня приближенно равна:
. Масса всего стержня приближенно равна:
 .
.
При стремлении  к нулю, эта сумма становится равной
к нулю, эта сумма становится равной  , то есть
, то есть 
Задача о площади криволинейной трапеции. Дана плоская фигура, ограниченная графиком функции  и отрезками прямых
и отрезками прямых 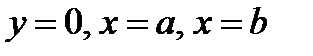 . Функция
. Функция  определена, не прерывна и неотрицательна в промежутке [а, b]. Вычислить площадь S полученной фигуры (аАВb), называемой криволинейной трапецией.
определена, не прерывна и неотрицательна в промежутке [а, b]. Вычислить площадь S полученной фигуры (аАВb), называемой криволинейной трапецией.
 Решение. Для того чтобы вычислить искомую площадь, разобьем промежуток [а, b] на nпроизвольных частей:
Решение. Для того чтобы вычислить искомую площадь, разобьем промежуток [а, b] на nпроизвольных частей:  , длины которых обозначим соответственно
, длины которых обозначим соответственно  . Через каждую точку деления проведем прямую, параллельную оси ординат. Эти прямые разделят данную фигуру на nполос. Заменим каждую из этих полос прямоугольником, основание которого то же, что у полосы, а высота совпадает с одной из ординат точек графика функции в этой полосе.
. Через каждую точку деления проведем прямую, параллельную оси ординат. Эти прямые разделят данную фигуру на nполос. Заменим каждую из этих полос прямоугольником, основание которого то же, что у полосы, а высота совпадает с одной из ординат точек графика функции в этой полосе.

Обобщим рассуждения, проведенные при решении двух предыдущих задач о массе прямолинейного стержня и о площади криволинейной трапеции. Пусть некоторая функция  задана на промежутке [а, b] и непрерывна. При разбиении промежутка [а, b] на n частей, таким образом, что максимальная длина отрезков разбиения стремится к нулю
задана на промежутке [а, b] и непрерывна. При разбиении промежутка [а, b] на n частей, таким образом, что максимальная длина отрезков разбиения стремится к нулю  при
при  ) обе задачи свелись к составлению суммы
) обе задачи свелись к составлению суммы  , где
, где  , число слагаемых которой неограниченно растет, а каждое слагаемое стремится к нулю. Эта сумма называется интегральной суммой.
, число слагаемых которой неограниченно растет, а каждое слагаемое стремится к нулю. Эта сумма называется интегральной суммой.
Определение. Предел  называют определенным интегралом от функции
называют определенным интегралом от функции 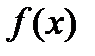 на промежутке [ а, b ] и обозначают
на промежутке [ а, b ] и обозначают 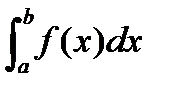 т. е.
т. е.
 (3.7)
(3.7)
Число  называется нижним пределом интеграла, b - верхним.
называется нижним пределом интеграла, b - верхним.
Промежуток [ а, b ] называется промежутком интегрирования, х - переменной интегрирования.
Теорема. Определенный интеграл функции 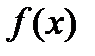 , непрерывной на промежутке [а, b], равен разности значений любой ее первообразной в точках b и а
, непрерывной на промежутке [а, b], равен разности значений любой ее первообразной в точках b и а
 (3.8)
(3.8)
: Правая часть формулы часто записывается как 
Формула (3.8) получила название формулы Ньютона-Лейбница.
Чтобы вычислить определенный интеграл, достаточно найти неопределенный интеграл и в полученное выражение подставить вместо переменной x; сначала верхний предел b, а затем нижний а и из первого результата вычесть второй.
Пример 3.10. Вычислить 
Решение. Находим неопределенный интеграл: 
Найдя значение  сначала при
сначала при 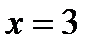 , а затем при
, а затем при 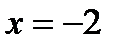 , вычислим разность:
, вычислим разность:
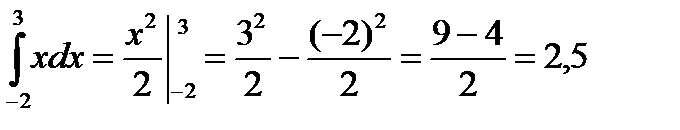
Пример 3.11. Вычислить 
Решение. 
При формулировке свойств определенных интегралов использовали источник [5] и исходили из предположения, что функции заданы и дифференцируемы на промежутке [ a, b ]
1)  , (3.9)
, (3.9)
т. е. интеграл суммы равен сумме интегралов слагаемых.
2) 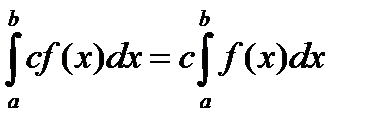 , (3.10)
, (3.10)
где  – константа; т. е. постоянный множитель можно выносить за знак интеграл.
– константа; т. е. постоянный множитель можно выносить за знак интеграл.
3) Пусть f (x) непрерывна на промежутке [ a, b ]. Если этот промежуток точкой c разложен на части [ a, c ] и [ c, b ], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.
 (3.11),
(3.11),
4) Если f (x) - любая функция, то:  , (3.12)
, (3.12)
т.е. интеграл с совпадающими нижним и верхним пределами равен нулю.
5)  , (3.13)
, (3.13)
то есть перемена мест пределов интегрирования приводит к изменению знака интеграла на противоположный.
6) Если f (x) - непрерывная функция, заданная на промежутке [ a, b ], то существует такая точка 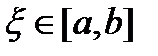 , что
, что  (3.14)
(3.14)
7) Если f (x) - неотрицательная непрерывная функция и нижний предел интеграла не больше верхнего, то и сам интеграл будет числом неотрицательным
 . (3.15)
. (3.15)
9) Если a ≤ b, а f (x) и u · g (x) - две непрерывные функции, которые на [ a, b ] удовлетворяют условию f (x) ≤ g (x), то
 (3. 16)
(3. 16)





 , его масса распределена неравномерно с плотностью
, его масса распределена неравномерно с плотностью  . Найти массу всего стержня.
. Найти массу всего стержня.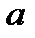 и
и  числовой оси
числовой оси  . Плотность вещества стержня в данной точке есть предел средней плотности
. Плотность вещества стержня в данной точке есть предел средней плотности  , где
, где 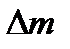 - масса отрезка
- масса отрезка  , при стремлении
, при стремлении  к нулю.
к нулю. достаточно малых частей (см. рис.)
достаточно малых частей (см. рис.) Обозначим длину отрезка
Обозначим длину отрезка  через
через  . В силу того, что длины отрезков малы, в границах каждого из них плотность стержня можно считать постоянной и равной
. В силу того, что длины отрезков малы, в границах каждого из них плотность стержня можно считать постоянной и равной  , где
, где  - одна из точек k-го отрезка
- одна из точек k-го отрезка  . Тогда масса этого отрезка стержня равна
. Тогда масса этого отрезка стержня равна  . Масса всего стержня приближенно равна:
. Масса всего стержня приближенно равна: .
. к нулю, эта сумма становится равной
к нулю, эта сумма становится равной  , то есть
, то есть 
 и отрезками прямых
и отрезками прямых 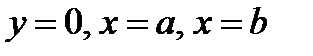 . Функция
. Функция  определена, не прерывна и неотрицательна в промежутке [а, b]. Вычислить площадь S полученной фигуры (аАВb), называемой криволинейной трапецией.
определена, не прерывна и неотрицательна в промежутке [а, b]. Вычислить площадь S полученной фигуры (аАВb), называемой криволинейной трапецией. Решение. Для того чтобы вычислить искомую площадь, разобьем промежуток [а, b] на nпроизвольных частей:
Решение. Для того чтобы вычислить искомую площадь, разобьем промежуток [а, b] на nпроизвольных частей:  , длины которых обозначим соответственно
, длины которых обозначим соответственно  . Через каждую точку деления проведем прямую, параллельную оси ординат. Эти прямые разделят данную фигуру на nполос. Заменим каждую из этих полос прямоугольником, основание которого то же, что у полосы, а высота совпадает с одной из ординат точек графика функции в этой полосе.
. Через каждую точку деления проведем прямую, параллельную оси ординат. Эти прямые разделят данную фигуру на nполос. Заменим каждую из этих полос прямоугольником, основание которого то же, что у полосы, а высота совпадает с одной из ординат точек графика функции в этой полосе.
 задана на промежутке [а, b] и непрерывна. При разбиении промежутка [а, b] на n частей, таким образом, что максимальная длина отрезков разбиения стремится к нулю
задана на промежутке [а, b] и непрерывна. При разбиении промежутка [а, b] на n частей, таким образом, что максимальная длина отрезков разбиения стремится к нулю  при
при  ) обе задачи свелись к составлению суммы
) обе задачи свелись к составлению суммы  , где
, где  , число слагаемых которой неограниченно растет, а каждое слагаемое стремится к нулю. Эта сумма называется интегральной суммой.
, число слагаемых которой неограниченно растет, а каждое слагаемое стремится к нулю. Эта сумма называется интегральной суммой. называют определенным интегралом от функции
называют определенным интегралом от функции 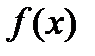 на промежутке [ а, b ] и обозначают
на промежутке [ а, b ] и обозначают 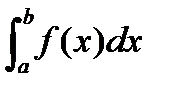 т. е.
т. е. (3.7)
(3.7) называется нижним пределом интеграла, b - верхним.
называется нижним пределом интеграла, b - верхним.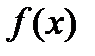 , непрерывной на промежутке [а, b], равен разности значений любой ее первообразной в точках b и а
, непрерывной на промежутке [а, b], равен разности значений любой ее первообразной в точках b и а (3.8)
(3.8)


 сначала при
сначала при 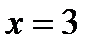 , а затем при
, а затем при 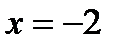 , вычислим разность:
, вычислим разность: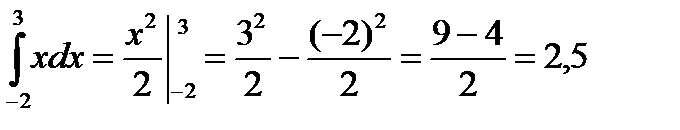


 , (3.9)
, (3.9)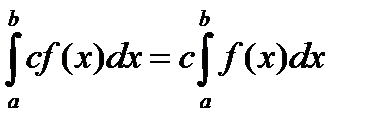 , (3.10)
, (3.10) – константа; т. е. постоянный множитель можно выносить за знак интеграл.
– константа; т. е. постоянный множитель можно выносить за знак интеграл. (3.11),
(3.11), , (3.12)
, (3.12) , (3.13)
, (3.13)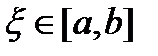 , что
, что  (3.14)
(3.14) . (3.15)
. (3.15) (3. 16)
(3. 16)


