

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Интересное:
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Функция F называется первообразной для функции f на некотором промежутке, если для всех х из этого промежутка существует производная F'(х), равная 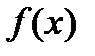 , т. е.
, т. е. 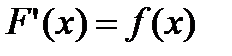 . (3.1)
. (3.1)
Пример 3.1. Найти первообразную для функции 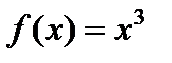 .
.
Решение. Функция 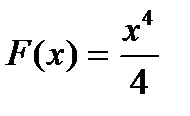 есть первообразная для функции
есть первообразная для функции 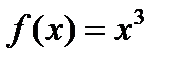 на промежутке
на промежутке 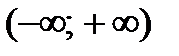 , так как
, так как 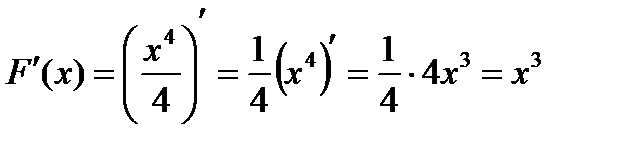 для всех
для всех 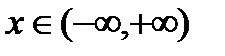 .
.
Но функции 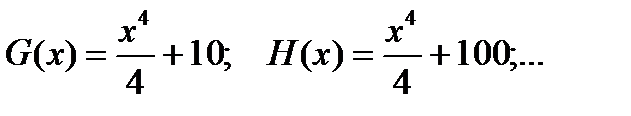 также имеют производную, равную
также имеют производную, равную 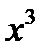 поэтому и все эти функции являются первообразными для функции
поэтому и все эти функции являются первообразными для функции 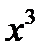 на множестве R.
на множестве R.
К выражению 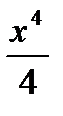 можно прибавить любую постоянную С. Поэтому решение задачи нахождения первообразной не единственно и, если решения существуют, то их бесконечно много.
можно прибавить любую постоянную С. Поэтому решение задачи нахождения первообразной не единственно и, если решения существуют, то их бесконечно много.
Множество первообразных для данной функции 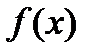 называется неопределенным интегралом и обозначается
называется неопределенным интегралом и обозначается  , (3.2).
, (3.2).
где 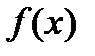 - подынтегральная функция;
- подынтегральная функция; 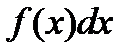 - подынтегральное выражение;
- подынтегральное выражение; 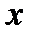 - переменная интегрирования; С - константа.
- переменная интегрирования; С - константа.
Пример 3.2. Найти неопределенный интеграл 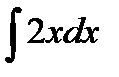 .
.
Решение 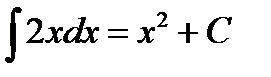
Интегрирование есть действие, обратное дифференцированию.
Неопределенные интегралы элементарных функций
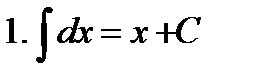
| 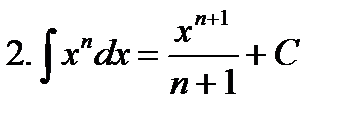 
| 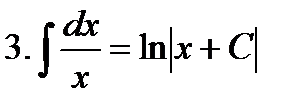
|
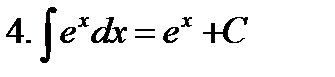
| 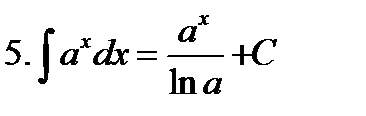
| 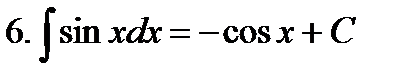
|
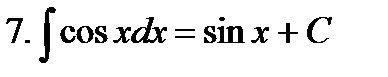
| 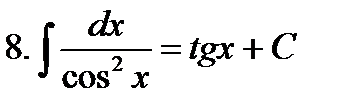
| 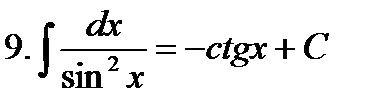
|
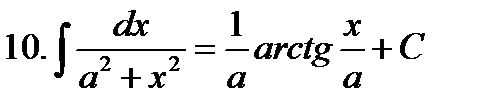
| 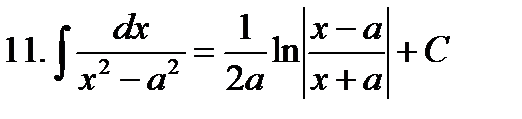
| 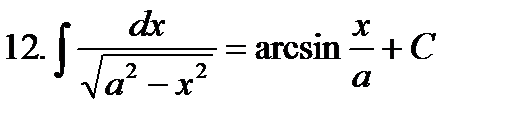
|
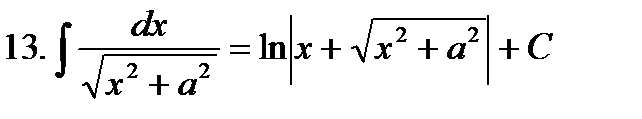
|
Свойства неопределенных интегралов:
1. Постоянный множитель можно вынести за знак интеграла:
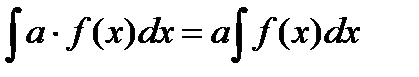 (3.3)
(3.3)
2. Интеграл алгебраической суммы равен алгебраической сумме интегралов:
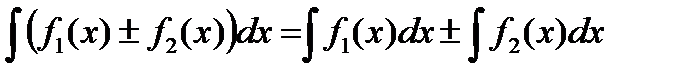 (3.4)
(3.4)
3. Вид интеграла не зависит от вида переменной интегрирования:
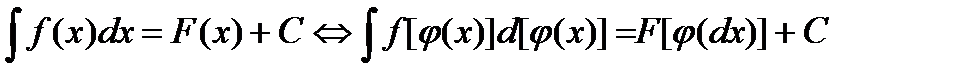 . (3.5)
. (3.5)
или, что тоже самое,
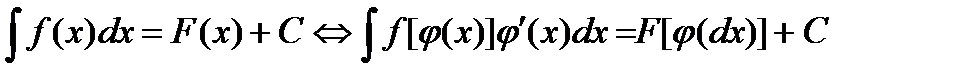 ,
,
где 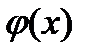 - функция, непрерывная вместе со своей производной.
- функция, непрерывная вместе со своей производной.
4. Имеет место следующее равенство:
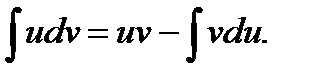 (3.6)
(3.6)
Методы интегрирования
I. Непосредственное интегрирование.
Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для решения табличные интегралы.
Пример 3.3. Найти 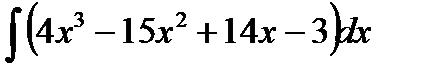
Решение. Воспользуемся свойством 2. интеграла: интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих же функций.

Пример 3.4. Найти 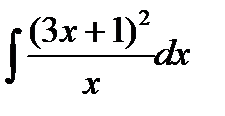
Решение. Приведем интеграл к табличному виду. Для этого раскроем скобки в числителе и разделим почленно числитель на знаменатель.
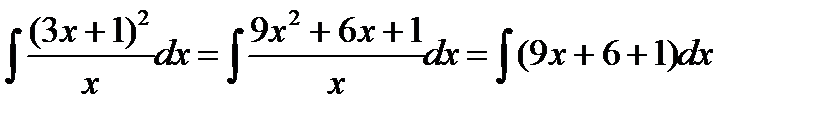
Затем воспользуемся указанным выше свойством интеграла суммы (разности) функций: 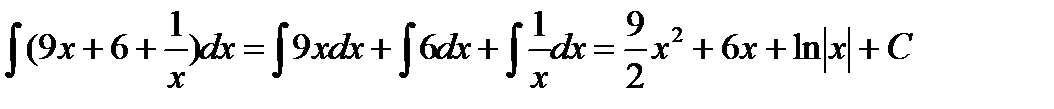
II. Метод подстановки.
Этот метод называют также методом замены переменной. Использование этого метода основано на свойстве 3 интеграла.
Пример 3.5. Найти 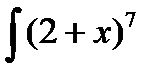
Решение. Введем новую переменную: 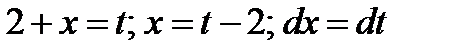 .
.
Найдем интеграл: 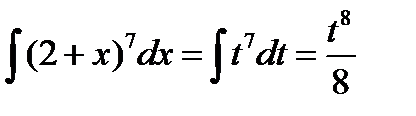
Выразим результат через первоначальный аргумент: 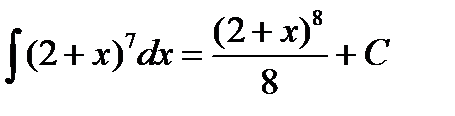
Пример 3.6. Найти 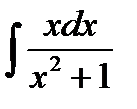
Решение. Сделаем подстановку  Надо определить, чему равен dx. Для этого продифференцируем выражение
Надо определить, чему равен dx. Для этого продифференцируем выражение 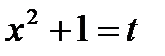 , в результате чего получим
, в результате чего получим 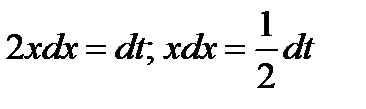 .
.
Подставим все это в первоначальный интеграл, в результате чего будем иметь:
|
|
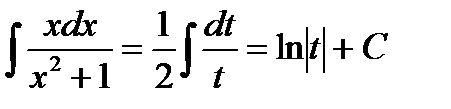
Выразим результат через первоначальный аргумент: 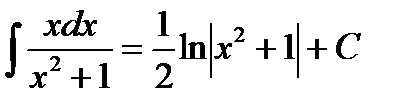
Этот пример дает возможность сделать следующий общий вывод: 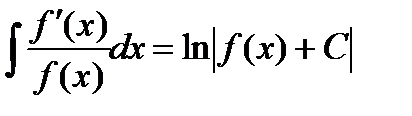 .
.
III. Метод интегрирования по частям.
Использование этого метода основано на свойстве (4) интеграла: 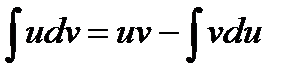
Пример 3.7. Найти 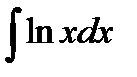 .
.
Решение. Обозначим 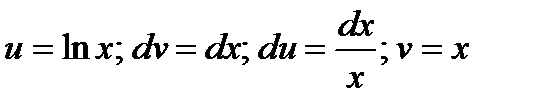 .
.
Подставим полученные данные в первоначальное выражение:
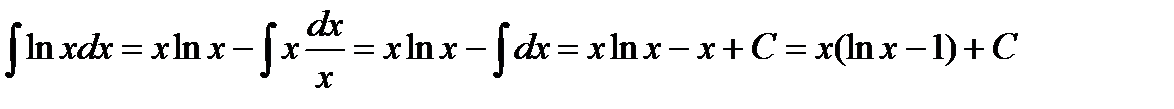
Пример 3.8. Найти 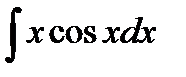 .
.
Решение. Интегрируем по частям

Тогда 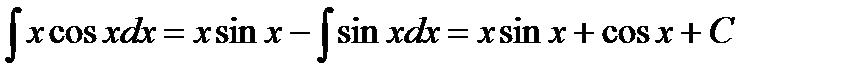
Пример 3.9. Найти 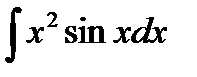
Решение. Интегрируем по частям
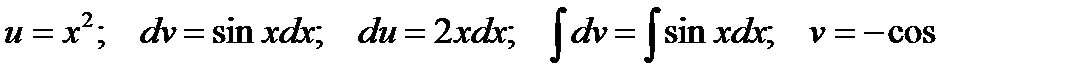
Тогда 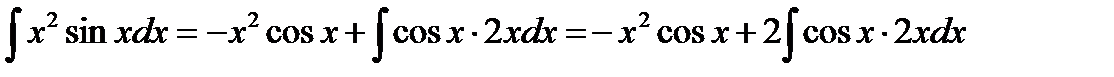 .
.
Подставим значение интеграла из примера 3.8, получим
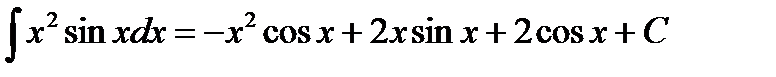
|
|
|

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!