Л Построение графика
Непрерывная линия называется выпуклой или обращенной выпуклостью вверх на отрезке [а, b], если все точки этой линии лежат выше хорды, соединяющей любые две ее точки.
Вогнутой (обращенной выпуклостью вниз) называется линия, проходящая ниже своих хорд.
Замечание. В некоторых руководствах выпуклость и вогнутость иногда определяются противоположным образом.
Точки, отделяющие выпуклые участки линии от вогнутых (и наоборот), называются точками перегиба.
На рисунках проиллюстрирован
геометрический смысл второй производной, позволяющий по ее знаку судить о том, в какую сторону изгибается линия графика, т. е. справедлива
Теорема. Если вторая производная функции  в данном промежутке значений х положительна:
в данном промежутке значений х положительна:
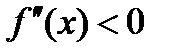 (2.10),
(2.10),
то кривая вогнута в этом промежутке, а если отрицательна:
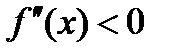 (2.11),
(2.11),
то кривая в этом промежутке выпукла.
Точками перегиба являются те точки, при переходе через которые вторая производная меняет знак.
Линия является выпуклой (или вогнутой ) в точке, если значение ее второй производной в данной точке меньше (или больше) нуля.
Пример.2.9. Выяснить, выпуклая или вогнутая линия  при
при  .
.
Решение. Находим производные  . В точке
. В точке  имеем:
имеем:  . Значит, в точке
. Значит, в точке 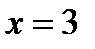 данная линия вогнута.
данная линия вогнута.
Нахождение точки перегиба. Чтобы исследовать функцию на вогнутость, необходимо определить знак второй производной. Если на данном промежутке f"(х) < 0 для всех х, то линия вогнута, если f"(х) > 0 для всех х, то линия выпукла. Выпуклую часть кривой от вогнутой отделяет точка перегиба.
Чтобы найти точку перегиба линии 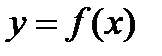 :
:
1. Найти вторую производную функции  .
.
2. Приравняв ее к нулю, решить полученное уравнение.
3. Расположив корни второй производной 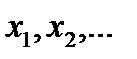 . в порядке возрастания, подставить в выражение для второй производной сначала любое число, меньшее
. в порядке возрастания, подставить в выражение для второй производной сначала любое число, меньшее 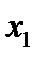 , затем - любое число
, затем - любое число  ; если получатся разные знаки, то при
; если получатся разные знаки, то при  имеется точка перегиба; если же одинаковые, то точки перегиба нет; далее аналогично поступить с числами
имеется точка перегиба; если же одинаковые, то точки перегиба нет; далее аналогично поступить с числами  .
.
4. Найти ординаты точек перегиба, т. е. найти значения функции в соответствующих точках.
Пример 2.10. Найти точки перегиба линии 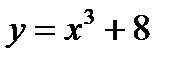 .
.
Решение. Находим:  .
.
Разобьем числовую прямую на интервалы:  ;
;  .
.
Определим знак второй производной в каждом из интервалов.
При переходе через  вторая производная меняет знак на противоположный, следовательно, при
вторая производная меняет знак на противоположный, следовательно, при 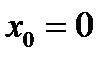 линия имеет перегиб.
линия имеет перегиб.
Ординату точки перегиба определим, подставив  в уравнение линии:
в уравнение линии:  Следовательно,
Следовательно, 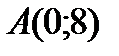 - точка перегиба.
- точка перегиба.
Пример 2.11. Найти точки перегиба линии  .
.
Решение. 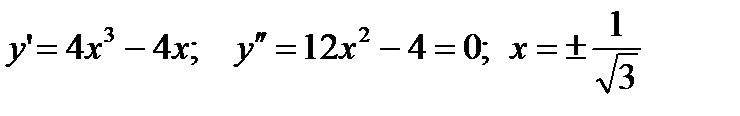
То есть, вторую производную можно разложить на множители:
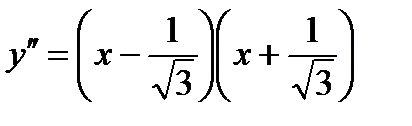
Разобьем числовую прямую на интервалы:
 ;
;
Определим знак второй производной в каждом из интервалов. В результате определим участки выпуклости-вогнутости функции.
| x
| 
| 
| 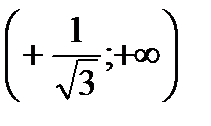
|

| +
| -
| +
|
| y
| вогнутая
| выпуклая
| вогнутая
|
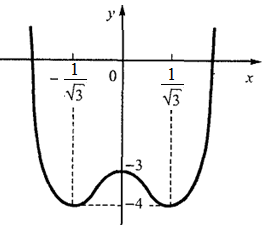 При
При 
 и
и  имеем
имеем  - линия вогнута;
- линия вогнута;
при  имеем
имеем  - линия выпукла.
- линия выпукла.
Точки  являются точками перегиба (см.рис.)
являются точками перегиба (см.рис.)
Рассмотрим последовательность выполнения операций при исследовании функции и построении ее графика на следующем примере.
Пример 2.12. Исследуйте функцию и постройте ее график 
Решение.
1) Область определения 
2) Функция не периодическая
3) Функция общего свойства, то есть не относится ни к четным, ни к нечетным.
3) Области возрастания-убывания.
 - функция возрастает;
- функция возрастает;
 - функция убывает.
- функция убывает.
4) Точки экстремумов: 

При  имеем минимум. Для определения значения этого минимума подставим
имеем минимум. Для определения значения этого минимума подставим  в уравнение кривой:
в уравнение кривой:  Таким образом, у графика функции имеется точка минимума с координатами (16; -32).
Таким образом, у графика функции имеется точка минимума с координатами (16; -32).
5) Точки пересечения с осями координат.
Для определения ординаты точки пересечения с осью  подставим в уравнение кривой
подставим в уравнение кривой  . В результате получим:
. В результате получим:  .
.
Таким образом, график функции пересекает ось  при
при  .
.
Для определения абсциссы точки пересечения с осью  подставим в уравнение кривой
подставим в уравнение кривой  . В результате получим:
. В результате получим:
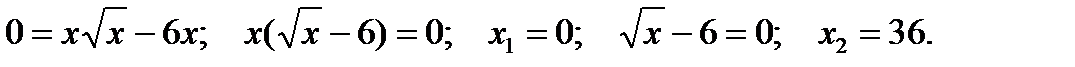
Таким образом, график функции пересекает ось  в двух точках: при
в двух точках: при  и
и  .
.
6) Области выпуклости-вогнутости.
Для определения участков вогнутости решаем неравенство:  . Оно справедливо для любого
. Оно справедливо для любого  из области определения. Следовательно, график функции всюду вогнут.
из области определения. Следовательно, график функции всюду вогнут.
Для определения участков выпуклости решаем неравенство:  . Оно не имеет решения. Следовательно, график функции не имеет участков выпуклости.
. Оно не имеет решения. Следовательно, график функции не имеет участков выпуклости.
7) Точки перегиба:
Для определения точек перегиба решаем уравнение:  . Оно не имеет решения. Следовательно, график функции не имеет точек перегиба.
. Оно не имеет решения. Следовательно, график функции не имеет точек перегиба.
8) Для построения графика функции начертим оси координат и отметим выявленные нами точки: минимума (16; -32) и пересечения с осями координат (0; 0) и (36; 0), а также области возрастания-убывания функции и ее вогнутости. В р 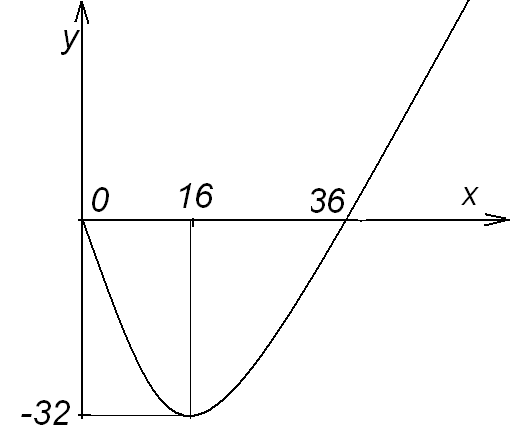 езультате получим график, изображённый на рисунке.
езультате получим график, изображённый на рисунке.
Дифференциал функции.
Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную 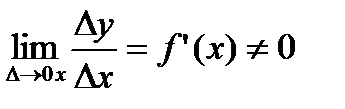 . Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать
. Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать
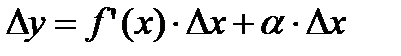 , (2.12)
, (2.12)
где α→0 при ∆х→0.
Таким образом, приращение функции ∆у представляет собой сумму двух слагаемых:  и
и  , являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как
, являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как 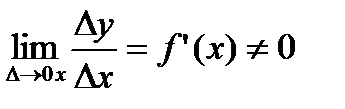 а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:
а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:
 . (2.13)
. (2.13)
Поэтому первое слагаемое  называют главной частью приращения функции ∆y. Дифференциалом функции
называют главной частью приращения функции ∆y. Дифференциалом функции  в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается
в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается  (или
(или 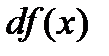 ):
):
 (2.14)
(2.14)
Дифференциал  называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции
называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции 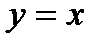 .
.
Так как 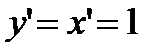 , то, согласно формуле (2.1), имеем
, то, согласно формуле (2.1), имеем  , т. е. дифференциал независимой переменной равен приращению этой переменной:
, т. е. дифференциал независимой переменной равен приращению этой переменной:
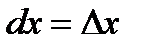 . (2.15)
. (2.15)
Поэтому формулу (2.14) можно записать так:
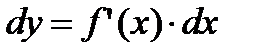 , (2.16)
, (2.16)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (2.16) следует равенство
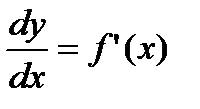 . (2.17)
. (2.17)
Теперь обозначение производной 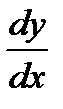 можно рассматривать как отношение дифференциалов
можно рассматривать как отношение дифференциалов  и
и 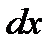 .
.
Пример 2.13
Найти дифференциал функции  .
.
Решение:
По формуле  находим
находим 
Пример 2.14. Найти дифференциал функции  . Вычислить
. Вычислить  при
при  .
.
Решение: 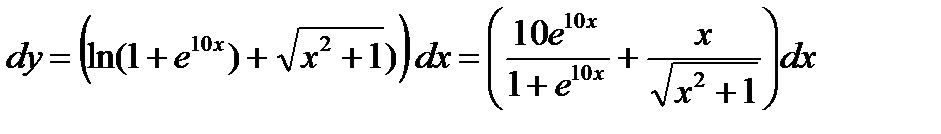 .
.
Подставив 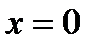 и
и  , получим
, получим 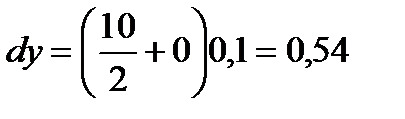 .
.






 в данном промежутке значений х положительна:
в данном промежутке значений х положительна: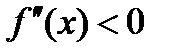 (2.10),
(2.10), при
при  .
. . В точке
. В точке  имеем:
имеем:  . Значит, в точке
. Значит, в точке 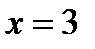 данная линия вогнута.
данная линия вогнута.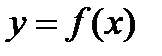 :
: .
.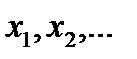 . в порядке возрастания, подставить в выражение для второй производной сначала любое число, меньшее
. в порядке возрастания, подставить в выражение для второй производной сначала любое число, меньшее 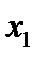 , затем - любое число
, затем - любое число  ; если получатся разные знаки, то при
; если получатся разные знаки, то при  имеется точка перегиба; если же одинаковые, то точки перегиба нет; далее аналогично поступить с числами
имеется точка перегиба; если же одинаковые, то точки перегиба нет; далее аналогично поступить с числами  .
.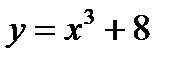 .
. .
. ;
;  .
.



 вторая производная меняет знак на противоположный, следовательно, при
вторая производная меняет знак на противоположный, следовательно, при 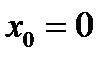 линия имеет перегиб.
линия имеет перегиб. Следовательно,
Следовательно, 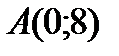 - точка перегиба.
- точка перегиба. .
.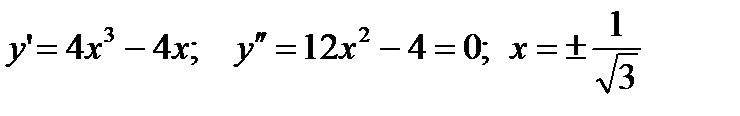
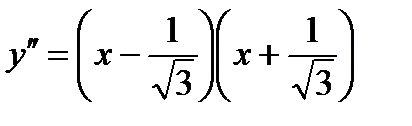
 ;
;

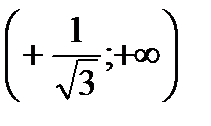

 При
При 
 и
и  имеем
имеем  - линия вогнута;
- линия вогнута; имеем
имеем  - линия выпукла.
- линия выпукла. являются точками перегиба (см.рис.)
являются точками перегиба (см.рис.)

 - функция возрастает;
- функция возрастает; - функция убывает.
- функция убывает.

 имеем минимум. Для определения значения этого минимума подставим
имеем минимум. Для определения значения этого минимума подставим  Таким образом, у графика функции имеется точка минимума с координатами (16; -32).
Таким образом, у графика функции имеется точка минимума с координатами (16; -32). подставим в уравнение кривой
подставим в уравнение кривой  . В результате получим:
. В результате получим:  .
. .
. подставим в уравнение кривой
подставим в уравнение кривой  . В результате получим:
. В результате получим: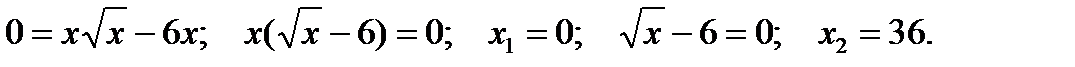
 в двух точках: при
в двух точках: при  и
и  .
. . Оно справедливо для любого
. Оно справедливо для любого  из области определения. Следовательно, график функции всюду вогнут.
из области определения. Следовательно, график функции всюду вогнут. . Оно не имеет решения. Следовательно, график функции не имеет участков выпуклости.
. Оно не имеет решения. Следовательно, график функции не имеет участков выпуклости. . Оно не имеет решения. Следовательно, график функции не имеет точек перегиба.
. Оно не имеет решения. Следовательно, график функции не имеет точек перегиба. езультате получим график, изображённый на рисунке.
езультате получим график, изображённый на рисунке.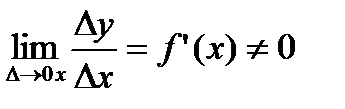 . Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать
. Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать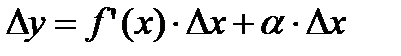 , (2.12)
, (2.12) и
и  , являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как
, являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как  . (2.13)
. (2.13) называют главной частью приращения функции ∆y. Дифференциалом функции
называют главной частью приращения функции ∆y. Дифференциалом функции  в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается
в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается  (или
(или 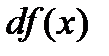 ):
): (2.14)
(2.14) называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции
называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции 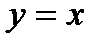 .
.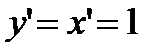 , то, согласно формуле (2.1), имеем
, то, согласно формуле (2.1), имеем  , т. е. дифференциал независимой переменной равен приращению этой переменной:
, т. е. дифференциал независимой переменной равен приращению этой переменной: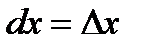 . (2.15)
. (2.15)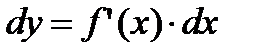 , (2.16)
, (2.16)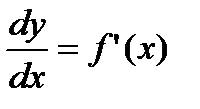 . (2.17)
. (2.17)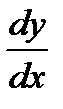 можно рассматривать как отношение дифференциалов
можно рассматривать как отношение дифференциалов  и
и 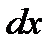 .
. .
. находим
находим 
 . Вычислить
. Вычислить  при
при  .
.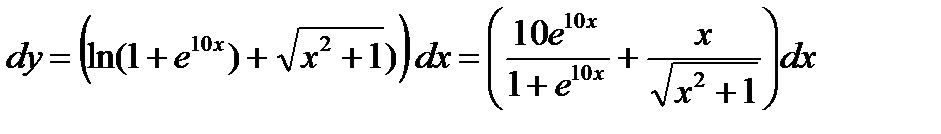 .
.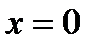 и
и  , получим
, получим 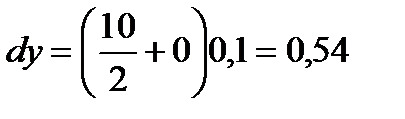 .
.


