Возрастание и убывание функции, ее экстремумы

 

Рассмотрим функцию 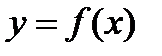, непрерывную вместе со своей про­изводной на некотором промежутке. Геометрический смысл производной заключается в том, что 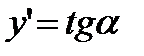, где 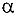-угол наклона касательной к положи­тельному направлению оси O х.

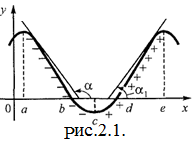
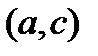Если с возрастанием значения аргумента х значение функции у убывает, то функция является убы­вающей (на рис. - в интервале ). Касательные, проведенные к кривой 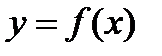в любой точке этого промежутка, образуют с осью 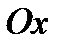тупой угол, тангенс которого отрицателен, т. е. для 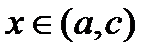величина 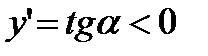. Значит, если функция убывает на некотором промежутке, то ее производная на этом промежутке отрицательна.

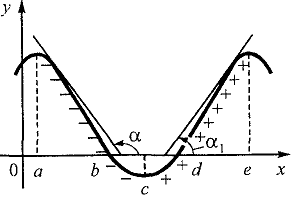
Если с возрастанием значения аргумента х значение функции yвоз­растает, то функция является возрастающей (на рис. в интервале 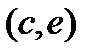).Касательные, проведенные к кривой у = f(х) в любой точке этого про­межутка, образуют с осью Ох острый угол, тангенс которого положите­лен, т. е. для 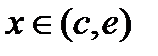величина 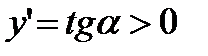. Значит, если функция воз­растает на некотором промежутке, то ее производная на этом проме­жутке положительна.

Теорема. Если функция f(x) имеет положительную производную в каждой точке интервала l, то эта функция возрастает на этом ин­тервале. Если функция f(x) имеет отрицательную производную в каждой точке интервала l, то эта функция убывает на этом интервале.

Замечание. Интервалы, в которых функция возрастает или убывает, называются интервалами монотонного изменения функции.

Мы предположили, что наша функция и ее производная непрерывны, а значит они меняют знаки с «-» на «+» или с «+» на «-» только при пе­реходе через нуль, т. е. в тех точках, в которых интервал убывания сменя­ется интервалом возрастания, (в которых у' = 0). В этих точках мгновен­ная скорость изменения функции равна нулю. Точки области определения функции, в которых производная функции равна нулю, бесконечности или не существует, называются критическими. На рис. 2.1. имеются три критические точки а, с, е.

 

Пример.2.7. Найти интервалы мо­нотонного изменения функции

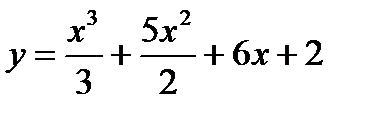
Решение. Найдем производную: .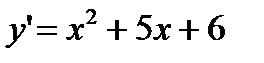

 

Эта функция непрерывна. Что­бы найти критические точки, при­равняем производную нулю и най­дем корни полученного уравнения:

Разобьем числовую прямую на интервалы: ; ; .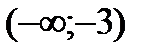

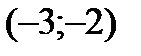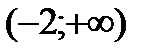Определим знак производной в каждом из интервалов. В результате определим участки возрастания-убывания функции.

x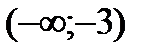
	+	-	+
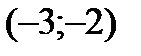
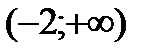
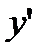
y	возрастает	убывает	возрастает

Таким образом, пр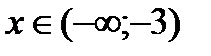и и 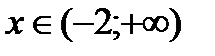функция возрастает, при 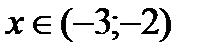- убывает.

Наименьшее значение функции в окрестности некоторой точки называют минимальным значением (min), а наибольшее ее значение - максимальным (max). Дадим строгое определение этим понятиям.

 

Точка 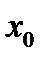из области определения функции f называ­ется точкой минимума этой функции, если у этой точки есть окрест­ность 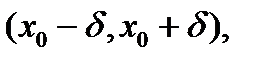во всех точках которой, не совпадающих с точкой ,

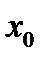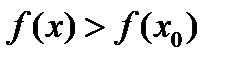(2.7)

Точка 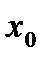из области определения функции f называ­ется точкой максимума этой функции, если у этой точки есть окре­стность 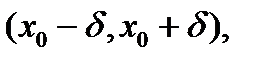во всех точках которой, не совпадающих с точкой ,

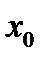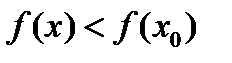(2.8)

Максимумы и минимумы называются экстремумами функции.

Замечание. Так как речь идет об экстремальных значениях функции в окрестностях некоторых точек, то иногда определенные нами экс­тремумы называются локальными экстремумами.

У непрерывной функции точки минимума и максимума обязатель­но чередуются.

Рассмотрим необходимое условие существования экстремума.

Теорема Ферма. Если внутренняя точка x _о из области определения непрерывной функции f(х) является точкой экстремума и в этой точке существует производная, то она равна нулю, т. е.

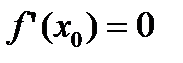(2.9)

 

Пример. 2.8. Исследовать на экстремум функцию .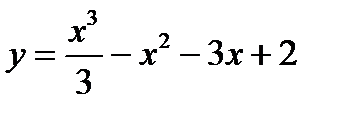

Решение. Функция 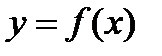точек разрыва не имеет. Область определения – вся числовая ось. Исследуем данную функцию на экстремум. Определим критические точки. Для этого находим первую производную данной функции и приравниваем ее к нулю: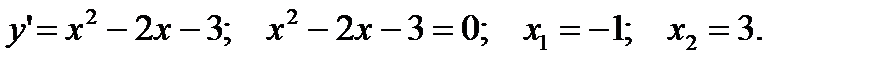

Разобьем числовую прямую на интервалы: ; ; .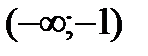

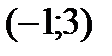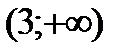Определим знак производной в каждом из интервалов. В результате определим участки возрастания-убывания функции.

x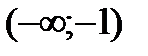
	+	-	+
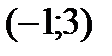
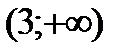
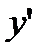
y		max при	min при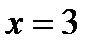

При 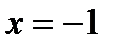производная меняет знак с «плюса» на «минус», то есть в этой точке функция имеет максимум. Для определения значения этого минимума подставим в первоначальное выражение функции 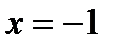, в результате получим .

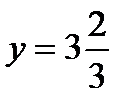При 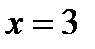производная меняет знак с «минуса» на «плюс», то есть в этой точке функция имеет минимум. Для определения значения этого максимума подставим в первоначальное выражение функции 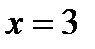, в результате получим .

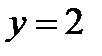Таким образом, функция 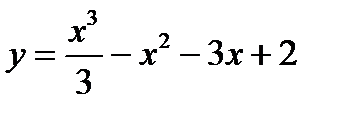имеет две точки экстремума:

- максимум; 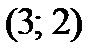- минимум.