Путь, пройденный телом при неравномерном движении за время 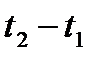 , вычисляется по формуле:
, вычисляется по формуле:
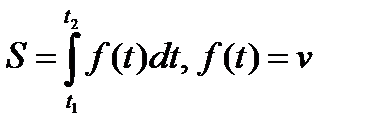 . (3.18)
. (3.18)
Пример 3.18. Скорость движения материальной точки задана уравнением 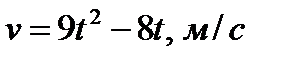 . Определить ее путь за четвертую секунду.
. Определить ее путь за четвертую секунду.
Решение. 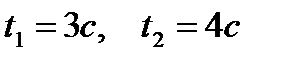
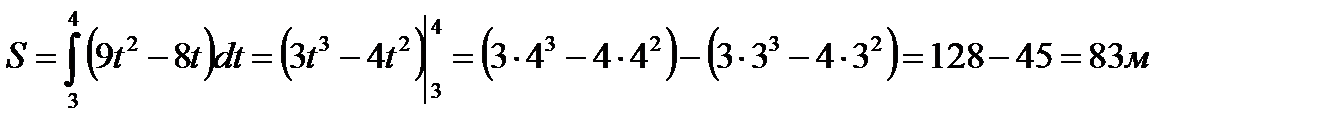 .
.
Ответ 83 м.
Пример 3.19. Скорость движения тела задана уравнением 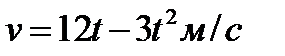 м/с. Определить путь, пройденный телом от начала движения до остановки.
м/с. Определить путь, пройденный телом от начала движения до остановки.
Решение Скорость движения тела равна пулю в моменты начала его движения и остановки. Найдем момент остановки тела, для чего приравняем скорость нулю и решим уравнение относительно t:
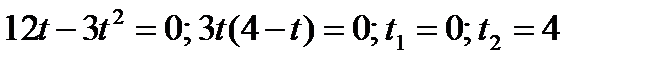
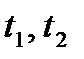 - пределы интегрирования.
- пределы интегрирования.
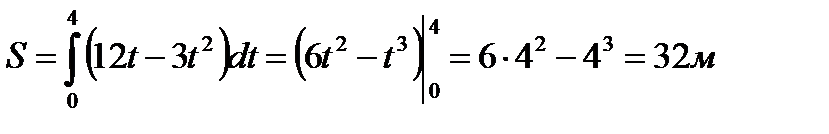
Ответ. S = 32 m.
Работа А, произведенная переменной силой 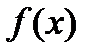 при перемещении тела oт
при перемещении тела oт 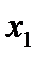 до
до 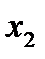 , вычисляется по формуле:
, вычисляется по формуле:
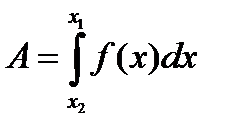 (3.19),
(3.19),
где 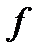 - в ньютонах (Н);
- в ньютонах (Н);  - в метрах (м);
- в метрах (м); 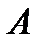 - в джоулях (Дж).
- в джоулях (Дж).
Пример 3.20. Сила в 8Н. растягивает пружину на 6см. Какую работу она производит?
Решение.
Согласно закону Гука 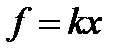 , где
, где 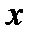 - величина растяжения,
- величина растяжения, 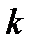 - коэффициент пропорциональности.
- коэффициент пропорциональности.
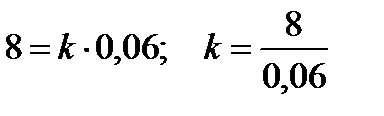
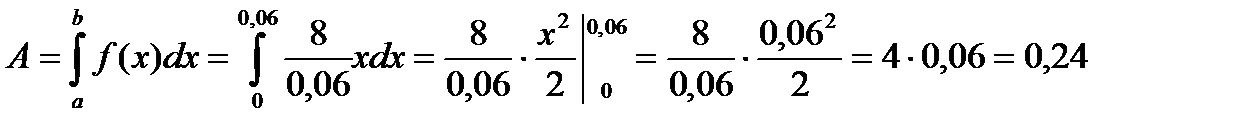 Дж.
Дж.
Ответ: 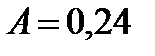 Дж.
Дж.
Формула вычисления силы 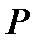 давления жидкости на пластинку, погруженную в жидкость:
давления жидкости на пластинку, погруженную в жидкость:
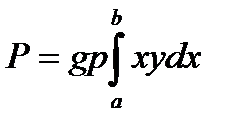 , (3.20)
, (3.20)
где а - глубина, на которой находится самая верхняя точка пластинки; b - глубина, на которой находится самая нижняя ее точка; х - расстояние точек пластинки до уровня жидкости; 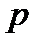 - плотность жидкости,
- плотность жидкости, 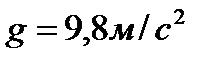 ,
, 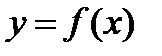 - функция, зависящая от формы пластинки;
- функция, зависящая от формы пластинки;
Пример 3.21. Треугольная пластинка с основанием 0,2 м и высотой 0,4 м погружена вертикально в воду так, что вершина ее лежит на поверхности воды, а основание параллельно ей (см. рис.). Вычислить силу давления воды па пластинку.
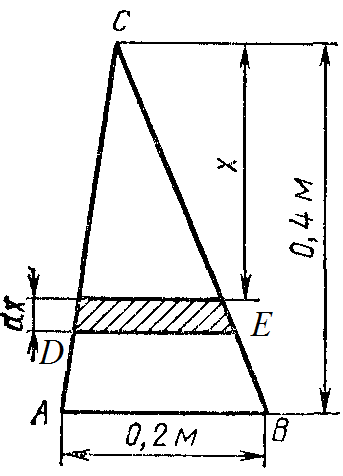 Решение. На глубине х выделим горизонтальную полоску шириной dx. Вычислим площадь полоски
Решение. На глубине х выделим горизонтальную полоску шириной dx. Вычислим площадь полоски 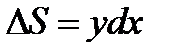 . Из подобия треугольника ABC и DEC имеем:
. Из подобия треугольника ABC и DEC имеем:
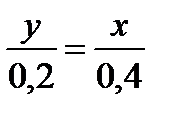 , откуда
, откуда 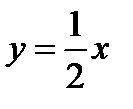 .
.
Тогда 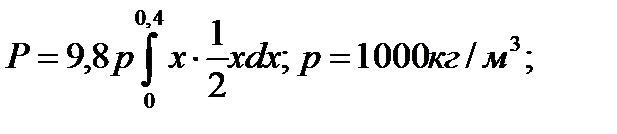
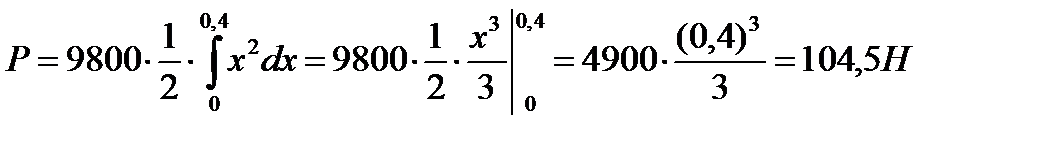
Ответ: 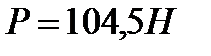
Приложение 1. ТАБЛИЦА ВАРИАНТОВ
| Вариант
| Номера задач
| Вариант
| Номера задач
|
|
| 7, 26, 69, 82, 101
|
| 1, 35, 55, 76, 110
|
|
| 14, 29, 54, 89, 104
|
| 2, 29, 54, 77, 104
|
|
| 20, 33, 59, 95, 108
|
| 3, 26, 51, 78, 101
|
|
| 9, 43, 67, 1, 118
|
| 4, 30, 56, 79, 105
|
|
| 12, 37, 65, 87, 112
|
| 11, 31, 52, 86, 106
|
|
| 10, 30, 58, 85, 105
|
| 9, 33, 74, 84, 108
|
|
| 19, 39, 68, 94, 114
|
| 7, 34, 53, 82, 109
|
|
| 11, 34, 60, 86, 109
|
| 8, 27, 57, 83, 102
|
|
| 15, 28, 64, 90, 103
|
| 5, 35, 58, 80, 110
|
|
| 2, 27, 53, 77, 102
|
| 23, 48, 73, 98, 123
|
|
| 4, 41, 52, 79, 116
|
| 25, 49, 72, 100, 124
|
|
| 18, 47, 51, 93, 122
|
| 6, 43, 67, 81, 118
|
|
| 5, 45, 66, 80, 120
|
| 10, 47, 71, 85, 122
|
|
| 21, 49, 62, 96, 124
|
| 12, 28, 53, 87, 103
|
|
| 25, 35, 61, 100, 110
|
| 24, 30, 56, 99, 105
|
|
| 17, 40, 56, 92, 115
|
| 22, 32, 57, 97, 107
|
|
| 8, 50, 63, 83, 125
|
| 13, 38, 63, 88, 113
|
|
| 23, 44, 71, 98, 119
|
| 23, 37, 64, 98, 112
|
|
| 1, 31, 55,76,106
|
| 14, 39, 65, 89, 114
|
|
| 6, 42, 70, 81, 117
|
| 22, 41, 66, 97, 116
|
|
| 3, 46, 74, 78, 121
|
| 21, 43, 68, 96, 118
|
|
| 22, 48, 73, 97, 123
|
| 15, 44, 67, 90, 119
|
|
| 13, 38, 75, 88, 113
|
| 20, 42, 69, 95, 117
|
|
| 24, 36, 72, 99, 111
|
| 19, 45, 70, 94, 120
|
|
| 16, 32, 57, 91, 107
|
| 18, 46, 71, 93, 121
|
|
| 4, 34, 68, 79, 109
|
| 7, 48, 69, 82, 123
|
|
| 2, 39, 58, 77, 114
|
| 1, 39, 54, 76, 114
|
|
| 15, 35, 65, 90, 110
|
| 3, 26, 68, 78, 101
|
|
| 11, 37, 67, 86,112
|
| 24, 34, 70, 99, 109
|
|
| 19, 43, 59, 94, 118
|
| 2, 40, 55, 77, 115
|
|
| 10, 33, 54, 85, 108
|
| 21, 31, 51, 96, 106
|
|
| 7, 43, 65, 82, 118
|
| 11, 35, 65, 86, 110
|
|
| 14, 34,64, 89, 109
|
| 17, 44, 59, 92, 119
|
|
| 1, 38, 72, 76, 113
|
| 5, 50, 75, 80, 125
|
|
| 6, 36, 57, 81, 111
|
| 23, 38, 58, 98, 113
|
|
| 23, 46, 74, 98, 121
|
| 12, 28, 53, 87, 103
|
|
| 16, 29, 75, 91, 104
|
| 8, 40, 63, 83, 115
|
|
| 24, 29, 59, 99, 104
|
| 10, 42, 52, 85, 117
|
|
| 21, 47, 53, 96, 122
|
| 6, 39, 53, 81, 114
|
|
| 18, 28, 60, 93, 103
|
| 16, 32, 57, 81, 107
|
|
| 3, 31, 63, 78, 106
|
| 13, 45, 60, 88, 120
|
|
| 5, 41, 51, 80, 116
|
| 14, 26, 56, 89, 101
|
|
| 8, 44, 70, 83, 119
|
| 22, 37, 62, 97, 112
|
|
| 9, 39, 74, 84, 114
|
| 4, 43, 61, 79, 118
|
|
| 12, 32, 75, 87, 107
|
| 18, 37, 56, 93, 112
|
|
| 1, 26, 51, 76, 101
|
| 20, 36, 67, 95, 111
|
|
| 5, 30, 55, 80, 105
|
| 15, 27, 66, 90, 102
|
|
| 4, 29, 54, 79, 104
|
| 9, 50, 71, 84, 125
|
|
| 8, 33, 63, 83, 108
|
| 19, 49, 58, 94, 124
|
|
| 25, 50, 75, 100, 125
|
| 25, 34, 74, 100, 109
|
Приложение 2. КОНТРОЛЬНЫЕ ЗАДАНИЯ
1-25. Выполнить действия. Результат представить в тригонометрической и показательной формах [5]:
1. 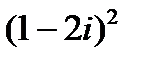
| 2. 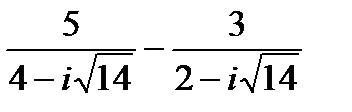
| 3. 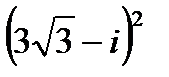
|
4. 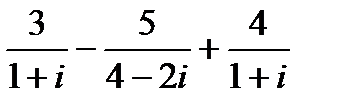
| 5. 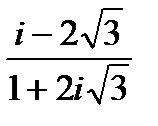
| 6. 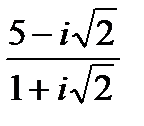
|
7. 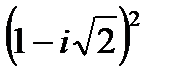
| 8. 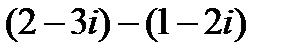
| 9. 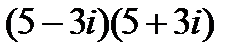
|
10. 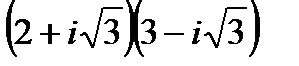
| 11. 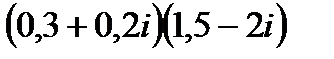
| 12. 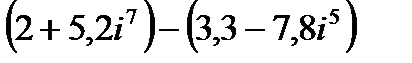
|
13. 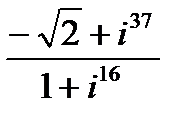
| 14. 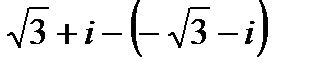
| 15. 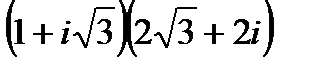
|
16. 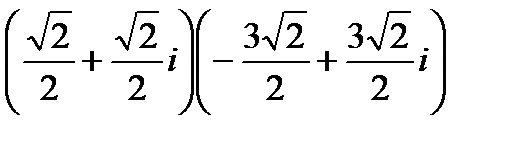
| 17. 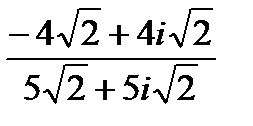
| 18. 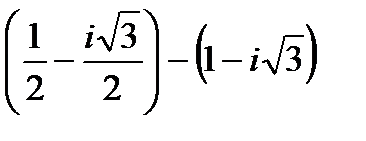
|
19. 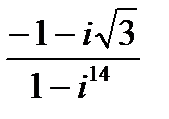
| 20. 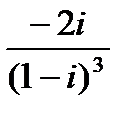
| 21. 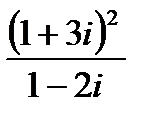
|
22. 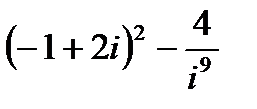
| 23. 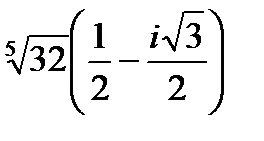
| 24. 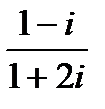
|
25. 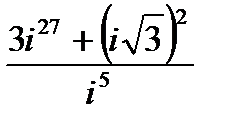
|
|
|
26-50. Найти производные функций [5]:
26. 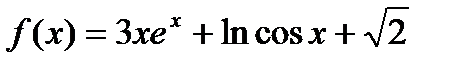 . Найти . Найти 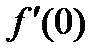
| 27. 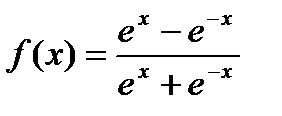
|
28. 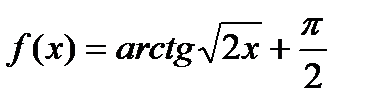 . Найти . Найти 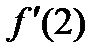
| 29. 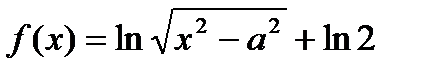
|
30. 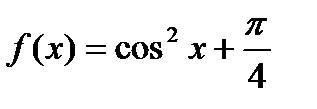 . Найти . Найти 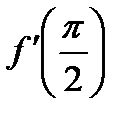
| 31. 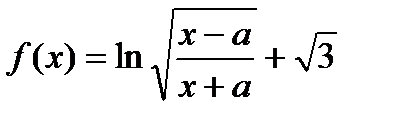
|
32. 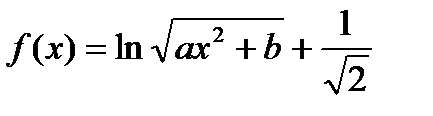
| 33. 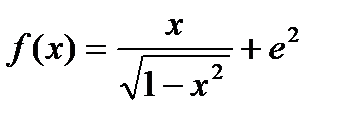
|
34. 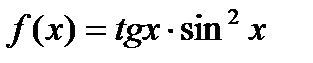
| 35. 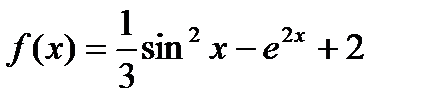
|
36. 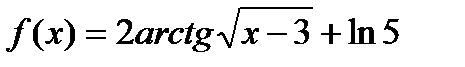 . Найти . Найти 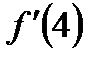
| 37. 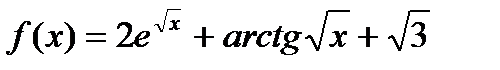
|
38. 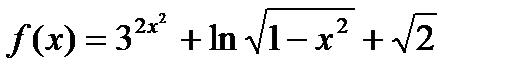
| 39. 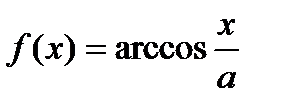
|
40. 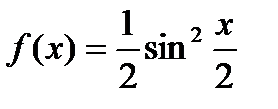 . Найти . Найти 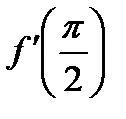
| 41. 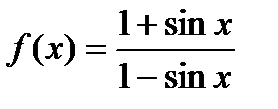
|
42. 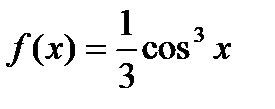 . Найти . Найти 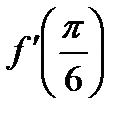
| 43. 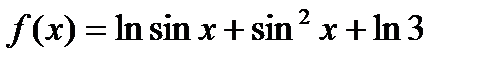
|
44. 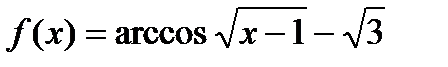
| 45. 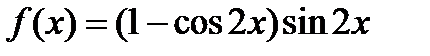
|
46. 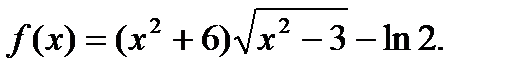 Найти Найти 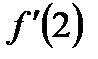
| 47. 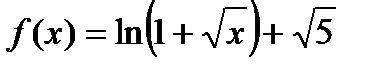 . Найти . Найти 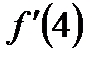
|
48. 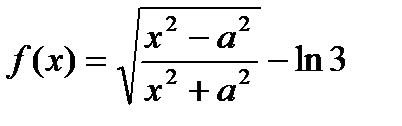
| 49. 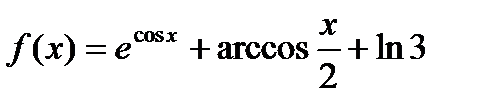
|
50. 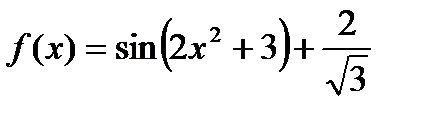
|
|
51-75. Решить задачи с использованием методов дифференцирования [5].
51. Написать равнение касательной к параболе 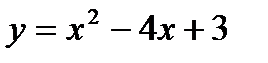 в точке, где
в точке, где 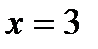 .
.
52. Определить ускорение точки в момент времени 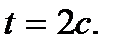 , если скорость точки, движущейся прямолинейно, задана уравнением
, если скорость точки, движущейся прямолинейно, задана уравнением 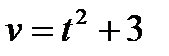 .
.
53. Тело движется прямолинейно по закону 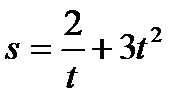 . Найти его скорость и ускорение, как функцию времени
. Найти его скорость и ускорение, как функцию времени 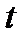 .
.
54. Написать равнения касательной и нормали к кривой 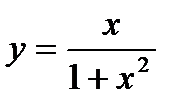 в точке
в точке 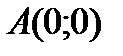 .
.
55. Материальная точка движется прямолинейно согласно уравнению 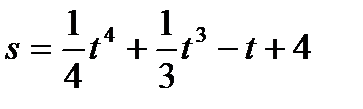 . Найти скорость и ускорение в конце второй секунды (путь в метрах).
. Найти скорость и ускорение в конце второй секунды (путь в метрах).
56. Материальная точка движется прямолинейно согласно уравнению 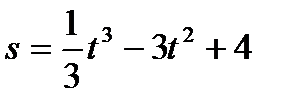 . Найти момент времени
. Найти момент времени  , когда скорость и ускорение тела равны нулю.
, когда скорость и ускорение тела равны нулю.
57. Материальная точка массы  движется прямолинейно согласно уравнению
движется прямолинейно согласно уравнению 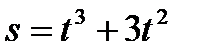 . Найти силу
. Найти силу 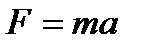 , действующую на эту точку, в момент времени
, действующую на эту точку, в момент времени 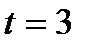 .
.
58. Написать равнения касательной и нормали к параболе 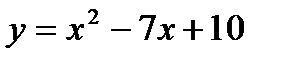 в точке
в точке 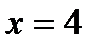 .
.
59. Найти, под какими углами парабола 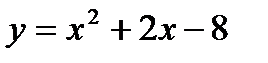 пересекает ось
пересекает ось 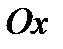 .
.
60. На параболе 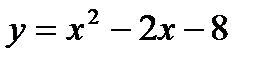 найти точку
найти точку 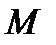 , в которой касательная к ней параллельна прямой
, в которой касательная к ней параллельна прямой 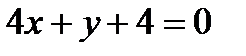 .
.
61. Построить график функции 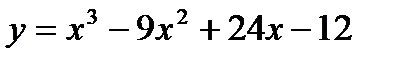 .
.
62. Разбить число 24 на два слагаемых, произведение которых будет наибольшим.
63. Построить график функции 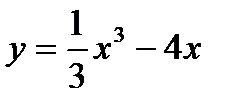 .
.
64. Разбить число 6 на два слагаемых так, чтобы сумма их квадратов была наименьшей.
65. Из куска проволоки длиной 5см. согнуть прямоугольник наибольшей площади.
66. Построить график функции 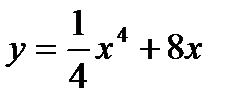 .
.
67. Найти максимум и минимум функции 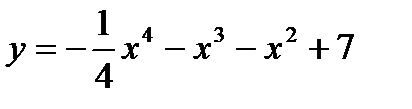 .
.
68. Тело движется по закону 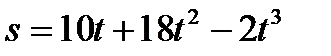 . Найти его максимальную скорость.
. Найти его максимальную скорость.
69. Построить график функции 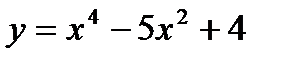 .
.
70. Из всех прямоугольников, вписанных в равнобедренный треугольник с основанием 10 см. и высотой 6 см. найти прямоугольник, имеющий наибольшую площадь.
71. Построить график функции 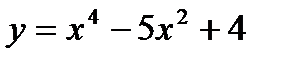 .
.
72. Исследовать на максимум и минимум функцию 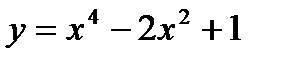 .
.
73. Разделить число 48 на две части, чтобы их произведение было наибольшим.
74. Исследовать на максимум и минимум функцию 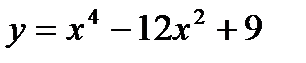 .
.
75. Найти дифференциал функции 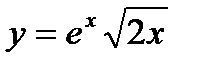
76-100. Найти интегралы [5]
101-125. Решить задачи с использованием определенных интегралов [5].
101. Найти площадь фигуры, ограниченной параболой 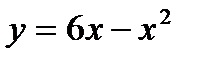 и осью
и осью 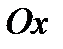 .
.
102. Найти площадь фигуры, ограниченной гиперболой 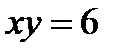 и прямой
и прямой 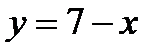 .
.
103. Вычислить объем тела, образованного вращением вокруг оси 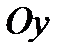 фигуры, ограниченной линиями
фигуры, ограниченной линиями 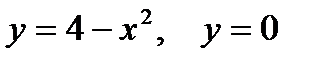 .
.
104. Найти площадь фигуры, ограниченной линиями 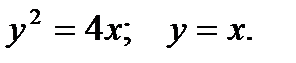
105. Сила 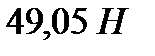 растягивает пружину на
растягивает пружину на 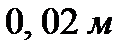 . Определить работу, затраченную на растяжение пружины до
. Определить работу, затраченную на растяжение пружины до 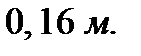 , если первоначальная длина пружины равна
, если первоначальная длина пружины равна 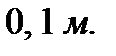
106. Определить давление воды на плотину, имеющую форму трапеции, верхнее основание которой равно 6,4 м., нижнее 4.2 м., а высота 3 м., если вода доходит до верха плотины.
107. Вычислить объем тела, образованного вращением вокруг оси 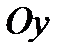 линии,
линии, 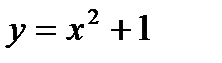 в пределах от
в пределах от 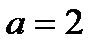 до
до 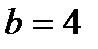 .
.
108. Найти площадь фигуры, ограниченной линиями 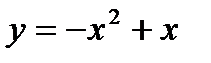 и
и 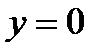 .
.
109. Вычислить объем тела, образованного вращением вокруг оси  площади, ограниченной линиями,
площади, ограниченной линиями, 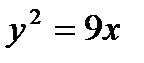 и
и 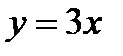 .
.
110. Два тела начали двигаться в один и тот же момент из одной точки в одном направлении по прямой. Одно тело двигалось со скоростью 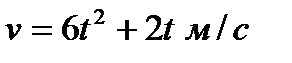 , другое – со скоростью
, другое – со скоростью 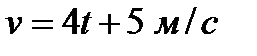 . На каком расстоянии они будут друг от друга через 5 с.?
. На каком расстоянии они будут друг от друга через 5 с.?
111. При сжатии пружины на 0,05 м. затрачивается работа 30 Дж. Какую работу надо совершить, чтобы сжать пружину на 0,08 м.?
112. Треугольная пластина с основанием 0,2 м. и высотой 0,4 м. погружена вертикально в воду так, что ее вершина лежит на поверхности воды, а основание параллельно ей. Вычислить силу давления воды на пластину.
113. Скорость движения точки задана уравнением 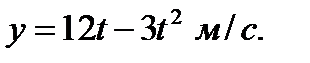 Найдите путь, пройденный телом от начала движения до его остановки.
Найдите путь, пройденный телом от начала движения до его остановки.
114. Найти площадь фигуры, ограниченной линиями; 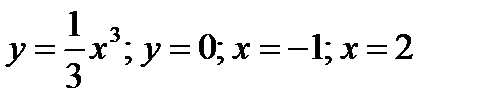 .
.
115. Пружина растягивается на 0,02 м. под действием силы 60 Н. Какую работу она производит, растягивая пружину на 0,12 м.?
116. Треугольная пластинка с основанием 0,4 м. и высотой 0,6 м. погружена вертикально в воду вертикально, так, что ее основание лежит на поверхности воды. Вычислить силу давления воды на пластинку.
117. Вычислить объем тела, образованного вращением вокруг оси  площади, ограниченной линиями,
площади, ограниченной линиями, 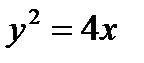 и
и 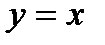 .
.
118. Найти площадь фигуры, ограниченной линиями 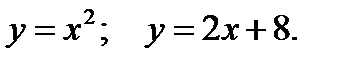
119. Найти площадь фигуры, ограниченной линиями 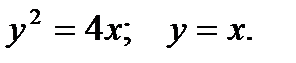
120. Для сжатия пружины на 0,05 м. затрачивается работа 10 Дж. На какую длину можно сжать пружину, совершив работу в 100 Дж?
121. Вычислить силу давления воды на вертикальную стенку, имеющую форму равнобедренной трапеции, верхнее основание которой, совпадающее с уровнем воды, равно 4,5 м., нижнее основание равно 3м., высота стенки составляет 3м.
122. Вычислить объем тела, образованного, вращением одной полуволны синусоиды 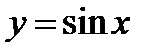 вокруг оси
вокруг оси 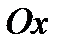 .
.
123. Найти площадь фигуры, ограниченной линиями 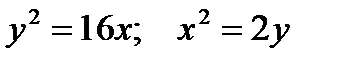
124. Вычислить объем тела, образованного вращением кривой 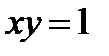 вокруг оси
вокруг оси 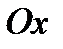 в пределах от
в пределах от 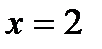 до
до 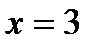 .
.
125. Прямоугольная пластинка с основанием 8 см. и высотой 10 см. погружена вертикально в воду, так, что ее верхнее основание находится на 2 см. ниже поверхности воды. Вычислить силу давления воды на пластинку.





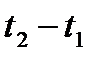 , вычисляется по формуле:
, вычисляется по формуле: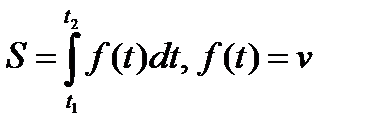 . (3.18)
. (3.18)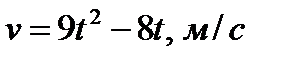 . Определить ее путь за четвертую секунду.
. Определить ее путь за четвертую секунду.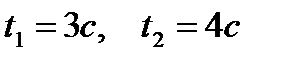
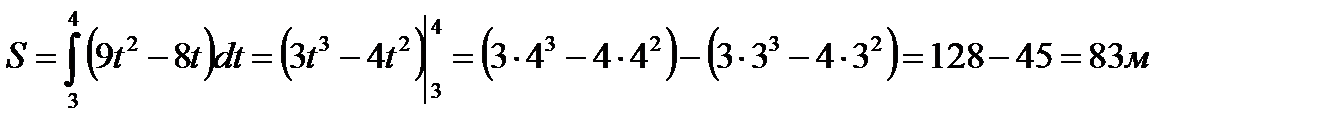 .
.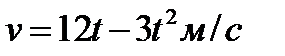 м/с. Определить путь, пройденный телом от начала движения до остановки.
м/с. Определить путь, пройденный телом от начала движения до остановки.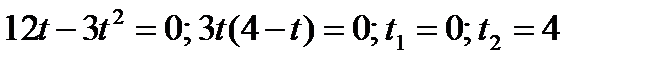
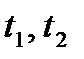 - пределы интегрирования.
- пределы интегрирования.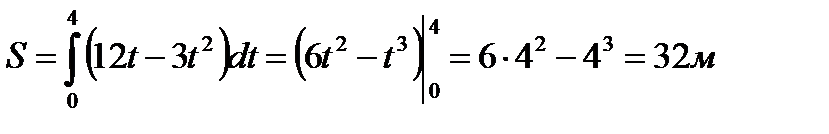
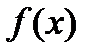 при перемещении тела oт
при перемещении тела oт 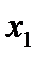 до
до 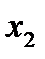 , вычисляется по формуле:
, вычисляется по формуле: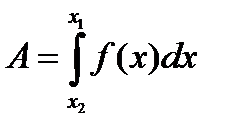 (3.19),
(3.19),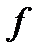 - в ньютонах (Н);
- в ньютонах (Н); 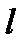 - в метрах (м);
- в метрах (м); 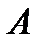 - в джоулях (Дж).
- в джоулях (Дж).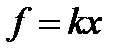 , где
, где 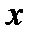 - величина растяжения,
- величина растяжения, 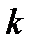 - коэффициент пропорциональности.
- коэффициент пропорциональности.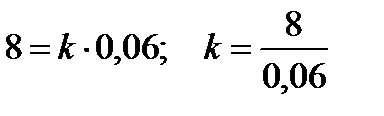
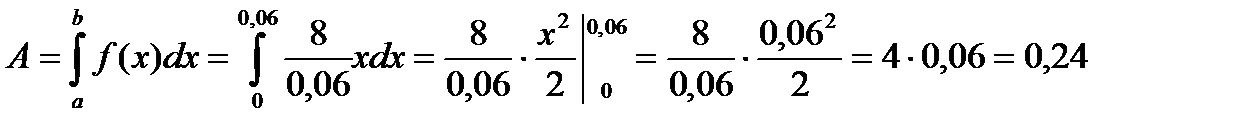 Дж.
Дж.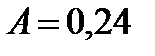 Дж.
Дж. давления жидкости на пластинку, погруженную в жидкость:
давления жидкости на пластинку, погруженную в жидкость: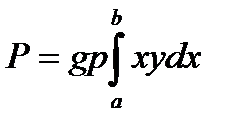 , (3.20)
, (3.20) - плотность жидкости,
- плотность жидкости, 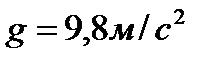 ,
, 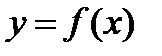 - функция, зависящая от формы пластинки;
- функция, зависящая от формы пластинки; Решение. На глубине х выделим горизонтальную полоску шириной dx. Вычислим площадь полоски
Решение. На глубине х выделим горизонтальную полоску шириной dx. Вычислим площадь полоски 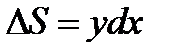 . Из подобия треугольника ABC и DEC имеем:
. Из подобия треугольника ABC и DEC имеем: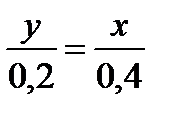 , откуда
, откуда 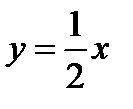 .
.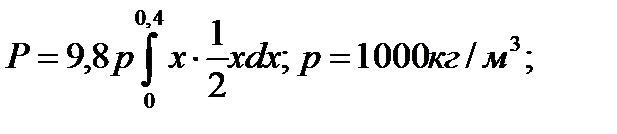
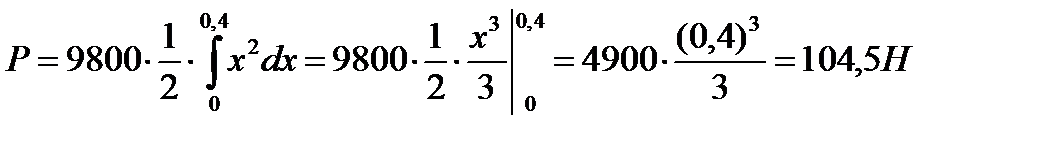
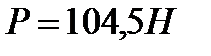
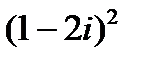
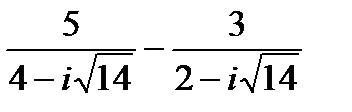
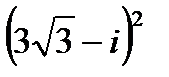
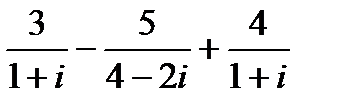
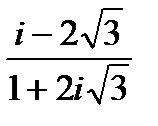
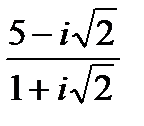
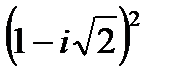
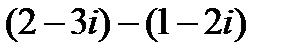
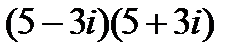
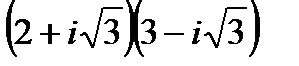
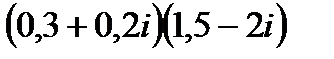
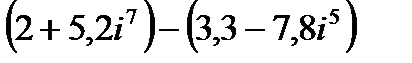
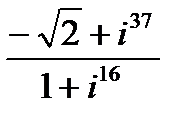
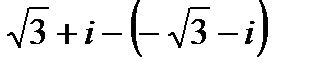
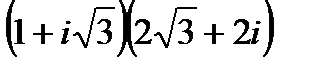
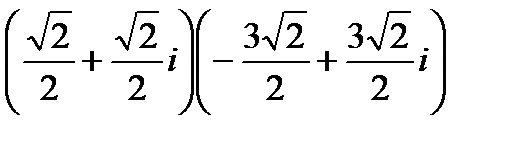
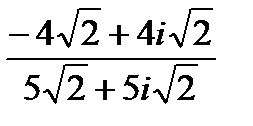
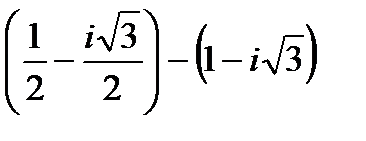
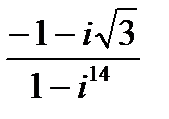
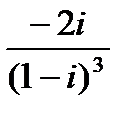
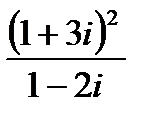
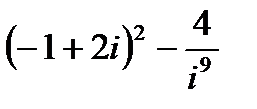
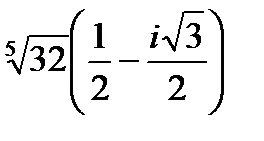
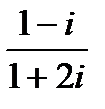
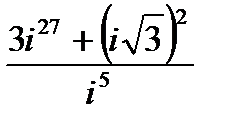
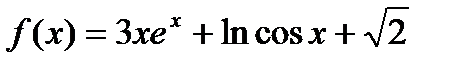 . Найти
. Найти 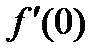
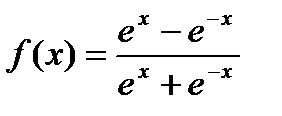
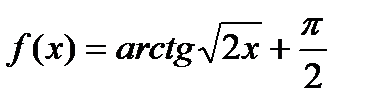 . Найти
. Найти 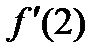
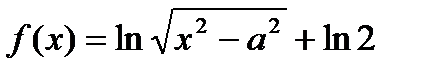
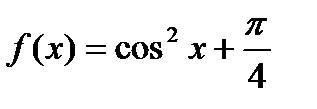 . Найти
. Найти 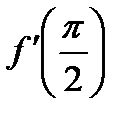
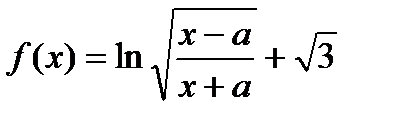
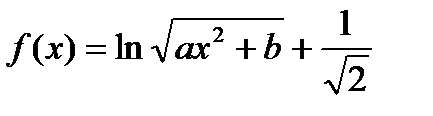
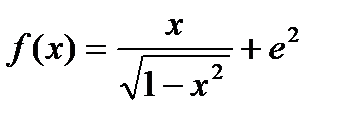
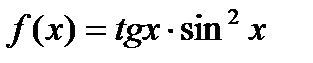
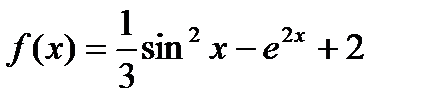
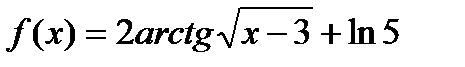 . Найти
. Найти 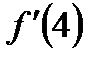
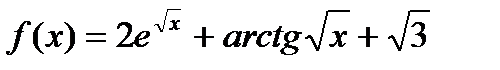
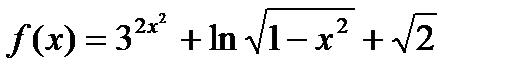
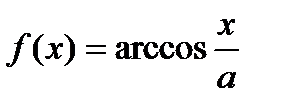
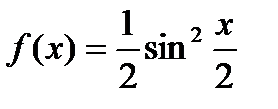 . Найти
. Найти 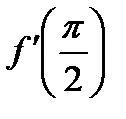
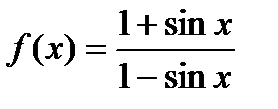
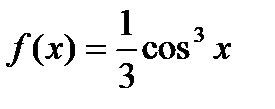 . Найти
. Найти 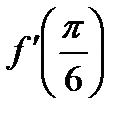
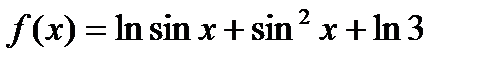
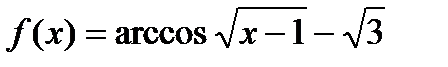
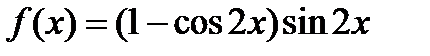
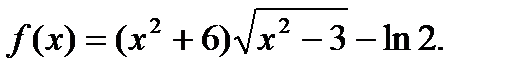 Найти
Найти 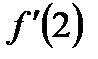
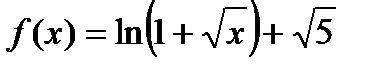 . Найти
. Найти 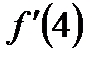
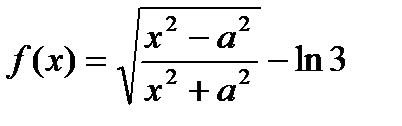
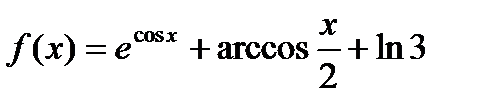
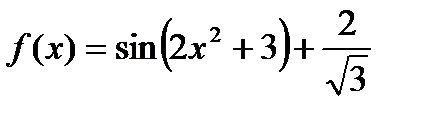
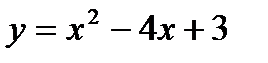 в точке, где
в точке, где 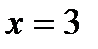 .
.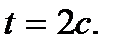 , если скорость точки, движущейся прямолинейно, задана уравнением
, если скорость точки, движущейся прямолинейно, задана уравнением 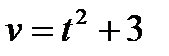 .
.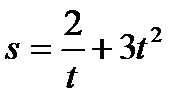 . Найти его скорость и ускорение, как функцию времени
. Найти его скорость и ускорение, как функцию времени 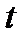 .
.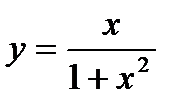 в точке
в точке  .
.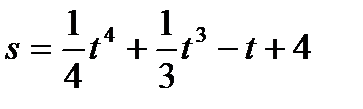 . Найти скорость и ускорение в конце второй секунды (путь в метрах).
. Найти скорость и ускорение в конце второй секунды (путь в метрах).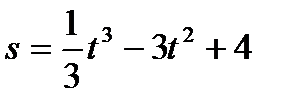 . Найти момент времени
. Найти момент времени 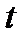 , когда скорость и ускорение тела равны нулю.
, когда скорость и ускорение тела равны нулю. движется прямолинейно согласно уравнению
движется прямолинейно согласно уравнению 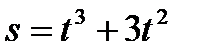 . Найти силу
. Найти силу 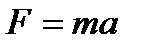 , действующую на эту точку, в момент времени
, действующую на эту точку, в момент времени 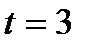 .
.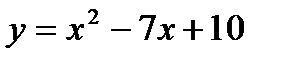 в точке
в точке 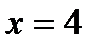 .
.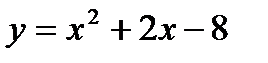 пересекает ось
пересекает ось  .
.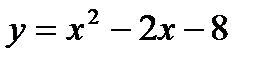 найти точку
найти точку 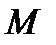 , в которой касательная к ней параллельна прямой
, в которой касательная к ней параллельна прямой 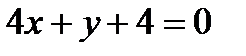 .
.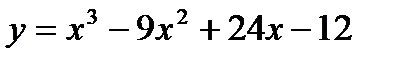 .
.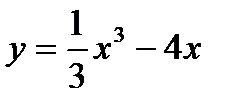 .
.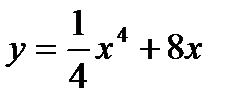 .
.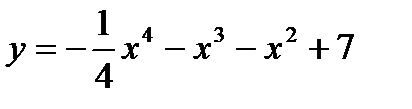 .
.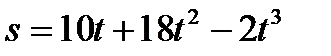 . Найти его максимальную скорость.
. Найти его максимальную скорость.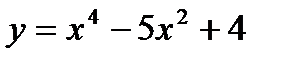 .
.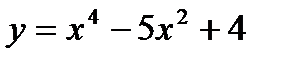 .
.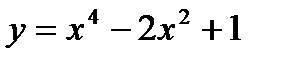 .
.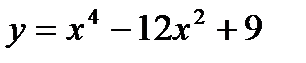 .
.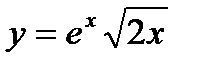
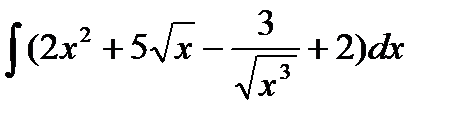
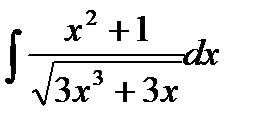
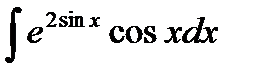
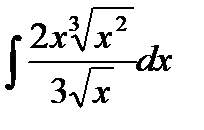
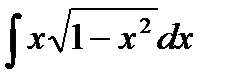
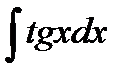
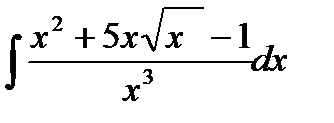
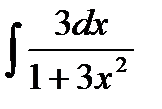
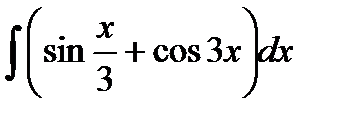
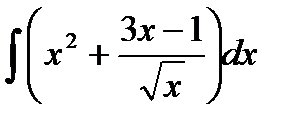
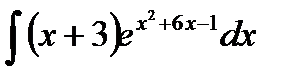
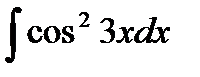
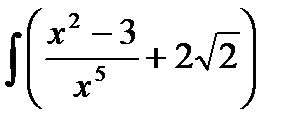
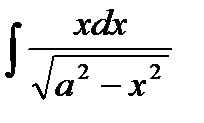
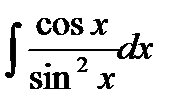
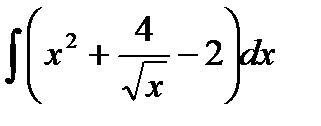
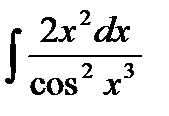
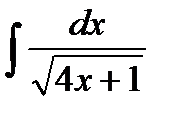
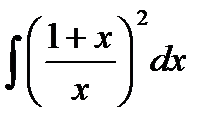
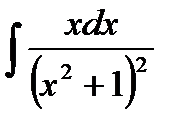
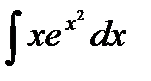
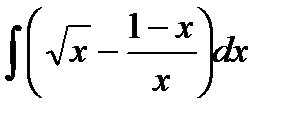
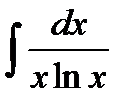
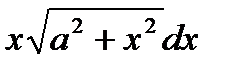
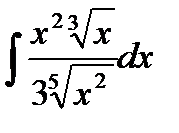
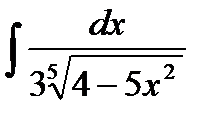
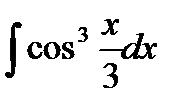
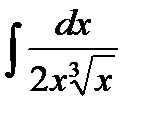
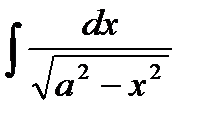
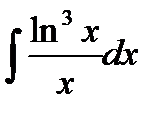
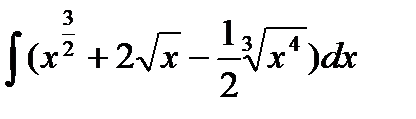
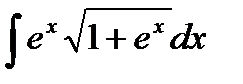
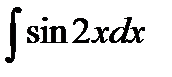
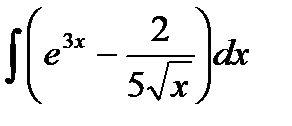
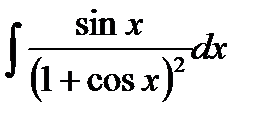
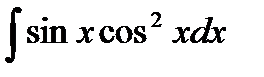
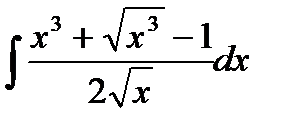
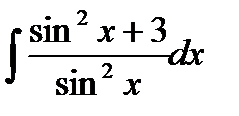
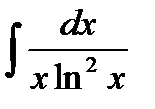
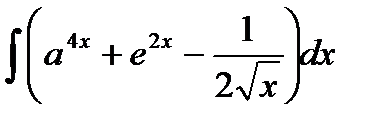
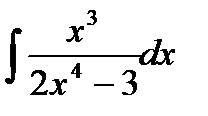
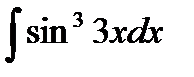
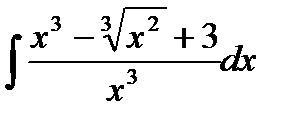
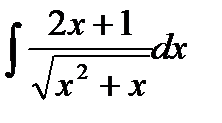
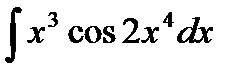
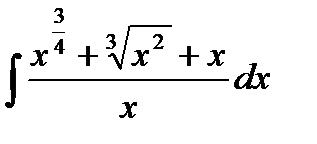
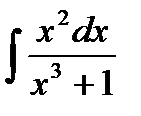
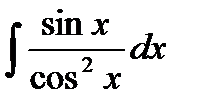
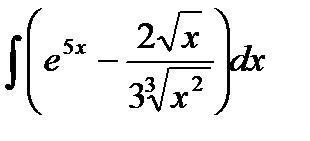
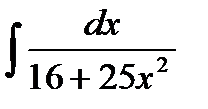
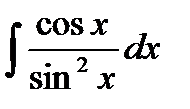
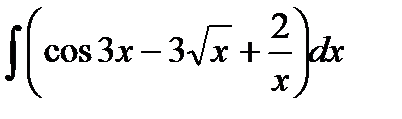
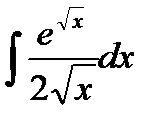
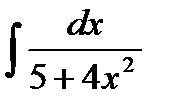
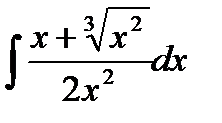
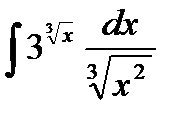
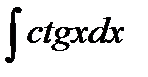
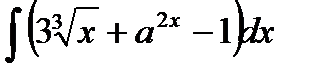
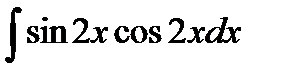
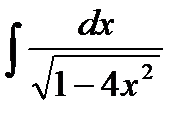
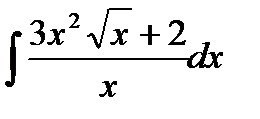
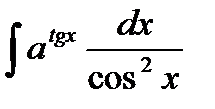
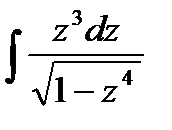
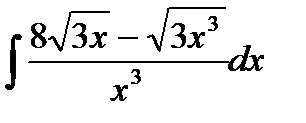
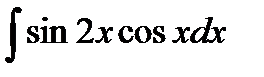
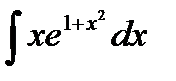
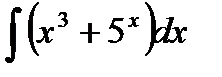
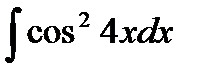
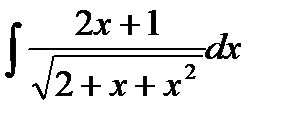
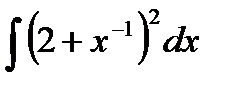
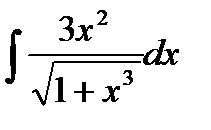
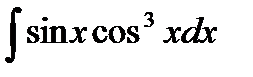
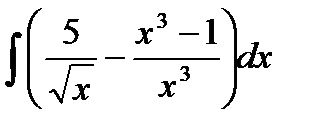
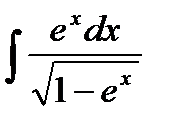
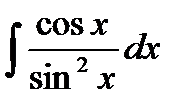
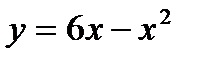 и осью
и осью  .
.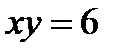 и прямой
и прямой 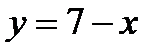 .
.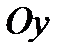 фигуры, ограниченной линиями
фигуры, ограниченной линиями 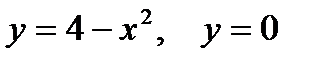 .
.
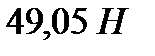 растягивает пружину на
растягивает пружину на 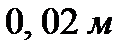 . Определить работу, затраченную на растяжение пружины до
. Определить работу, затраченную на растяжение пружины до 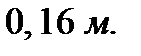 , если первоначальная длина пружины равна
, если первоначальная длина пружины равна 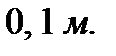
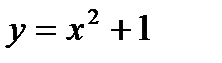 в пределах от
в пределах от 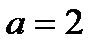 до
до 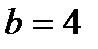 .
.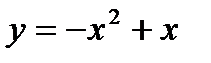 и
и 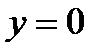 .
.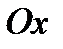 площади, ограниченной линиями,
площади, ограниченной линиями, 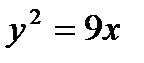 и
и 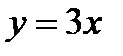 .
.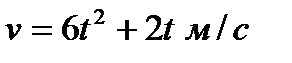 , другое – со скоростью
, другое – со скоростью 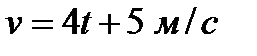 . На каком расстоянии они будут друг от друга через 5 с.?
. На каком расстоянии они будут друг от друга через 5 с.?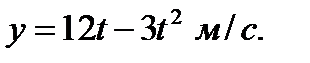 Найдите путь, пройденный телом от начала движения до его остановки.
Найдите путь, пройденный телом от начала движения до его остановки.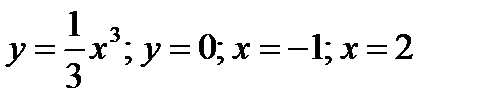 .
.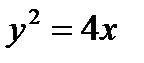 и
и 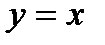 .
.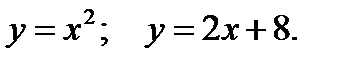
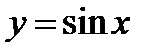 вокруг оси
вокруг оси  .
.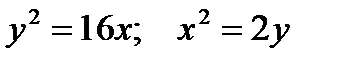
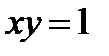 вокруг оси
вокруг оси 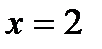 до
до 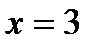 .
.


