Цель: Формирование навыков вычисления определенного интеграла при помощи формулы Ньютона – Лейбница
На выполнение работы отводится 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Функция, 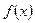 интегрируемая на промежутке
интегрируемая на промежутке 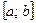 , если при любых разбиениях
, если при любых разбиениях  промежутка
промежутка  , таких, что
, таких, что 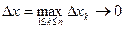 при произвольном выборе точек
при произвольном выборе точек 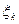 (где
(где 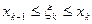 ), сумма
), сумма 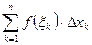 при
при 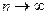 стремится к пределу
стремится к пределу 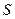 .
.
Предел 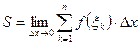 называют определенным интегралом от функции
называют определенным интегралом от функции 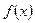 на промежутке
на промежутке 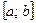 и обозначают
и обозначают 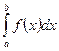 , то есть
, то есть 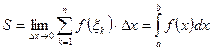 . (15.1)
. (15.1)
Число 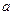 называется нижним пределом интеграла,
называется нижним пределом интеграла, 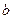 - верхним. Промежуток
- верхним. Промежуток 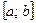 называется промежутком интегрирования,
называется промежутком интегрирования, 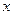 - переменной интегрирования.
- переменной интегрирования.
Для вычисления определенного интеграла от функции 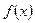 в том случае, когда можно найти соответствующий неопределенный интеграл
в том случае, когда можно найти соответствующий неопределенный интеграл 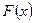 , служит формула Ньютона – Лейбница:
, служит формула Ньютона – Лейбница: 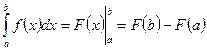 . (15.2). То есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
. (15.2). То есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
Примеры
Вычислить следующие определенные интегралы:
1) 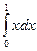 ; 2)
; 2) 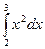 ; 3)
; 3) 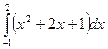 .
.
Решение: 1) 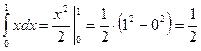 ; 2)
; 2) 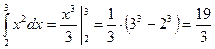 ;
;
3) 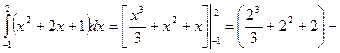
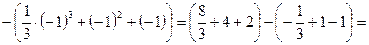
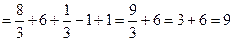
Задания для практической работы
Вычислите определенные интегралы:
1) 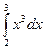 ; 2)
; 2) 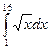 ; 3)
; 3) 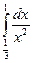 ; 4)
; 4) 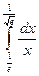 ; 5)
; 5) 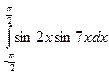
6) 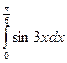 7)
7) 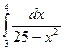 ; 8)
; 8) 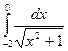 ; 9)
; 9) 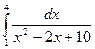 ;
;
10) 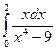 ; 11)
; 11) 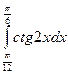 ; 12)
; 12) 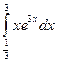 ; 13)
; 13) 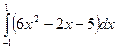 .
.
Контрольные вопросы:
1. Что называется интегральной суммой для функции на отрезке?
2. Дайте определение определенного интеграла.
3. Сформулируйте основные свойства определенного интеграла.
4. В чем заключается суть формулы Ньютона – Лейбница?
5. Сформулируйте теорему о среднем.
6. Перечислите основные методы интегрирования для определенного интеграла.
7. Запишите формулы, которые соответствуют вышеперечисленным методам интегрирования.
Рекомендуемая литература: 11.1 [с. 271-282], 1.2 [с. 205-212], 1.3 [с. 374-396], 2.2 [с. 247-250].
Практическая работа №16
Тема: Вычисление площадей фигур с помощью определенных интегралов
Цель: Формирование навыков вычисления площадей фигур с помощью определенных интегралов
Время выполнения: 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Определенный интеграл широко применяется при вычислениях различных геометрических фигур и физических величин.
Найдем площадь  криволинейной трапеции, ограниченной кривой
криволинейной трапеции, ограниченной кривой 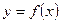 , осью
, осью 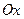 и двумя прямыми
и двумя прямыми 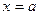 и
и 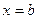 , где
, где 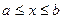 ,
, 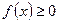 (рис.2).
(рис.2).
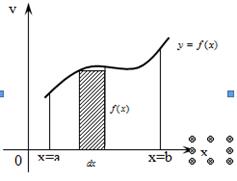
Рисунок 2 - Трапеция, ограниченная кривой 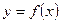 , осью
, осью 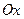 и двумя прямыми
и двумя прямыми 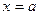 и
и 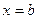 , где
, где 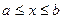 .
.
Так как дифференциал переменной площади 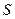 есть площадь прямоугольника с основанием
есть площадь прямоугольника с основанием  и высотой
и высотой 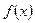 , то есть
, то есть 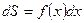 , то, интегрируя это равенство в пределах от
, то, интегрируя это равенство в пределах от 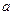 до
до 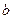 , получим
, получим 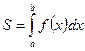 .
.
 основанием
основанием  и высотой
и высотой 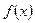 , то есть
, то есть 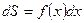 , то, интегрируя это равенство в пределах от
, то, интегрируя это равенство в пределах от 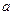 до
до 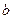 , получим
, получим 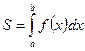 .
.
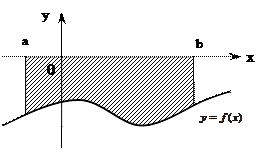
Если криволинейная трапеция прилегает к оси 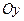 так, что
так, что 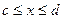 ,
, 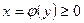 (рис.3), то дифференциал переменной площади
(рис.3), то дифференциал переменной площади 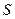 равен
равен 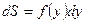 , откуда
, откуда 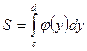 .
.

| | | | | | |
| | |  |
| |
| | Рисунок 3 -Трапеция, прилегает к оси  так, что так, что 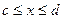 , , 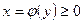
| | | Рисунок 4 - Трапеция, ограниченная кривой 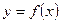 , осью , осью 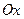 и прямыми и прямыми 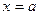 и и 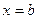 лежит под осью лежит под осью 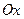
| |
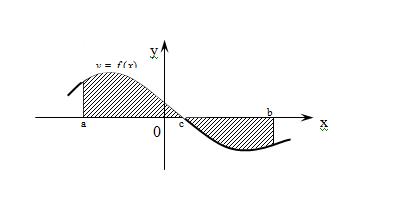
Рисунок 5 - Трапеция, ограниченная кривой 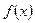 , осью
, осью 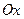 и прямыми
и прямыми
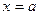 и
и 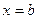 , расположена по обе стороны от оси
, расположена по обе стороны от оси 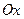 .
.
В том случае, когда криволинейная трапеция, ограниченная кривой 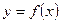 , осью
, осью 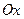 и прямыми
и прямыми 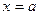 и
и 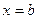 , лежит под осью
, лежит под осью 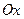 (рис.4), площадь находится по формуле
(рис.4), площадь находится по формуле 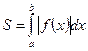 .
.
Если фигура, ограниченная кривой 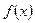 , осью
, осью 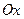 и прямыми
и прямыми 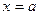 и
и 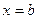 , расположена по обе стороны от оси
, расположена по обе стороны от оси 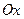 (рис. 5), то
(рис. 5), то 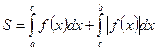 .
.
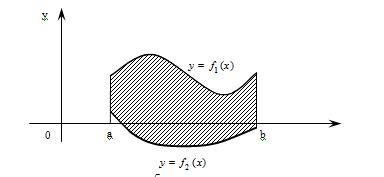
Рисунок 6 - Трапеция, двумя пересекающимися кривыми
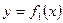 и
и 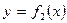 , прямыми
, прямыми 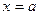 и
и 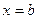 .
.
Пусть фигура 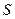 ограничена двумя пересекающимися кривыми
ограничена двумя пересекающимися кривыми 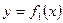 и
и 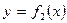 , и прямыми
, и прямыми 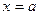 и
и 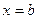 , где
, где 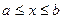 и
и 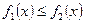 (рис. 6) Тогда ее площадь находится по формуле
(рис. 6) Тогда ее площадь находится по формуле 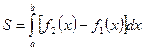 .
.
Примеры
Задание: Вычислить площади фигур, ограниченных указанными линиями 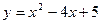 ,
, 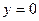 ,
, 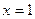 и
и 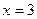 (рис. 7).
(рис. 7).

Рисунок 7 - Фигура, ограниченная указанными линиями
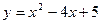 ,
, 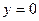 ,
, 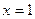 и
и 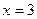 .
.
Решение: 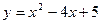 квадратичная функция;
квадратичная функция; 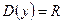 ; график – парабола, ветви направлены вверх.
; график – парабола, ветви направлены вверх.
Найдемкоординаты вершины параболы:
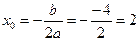 , отсюда следует, что
, отсюда следует, что 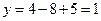 . Таким образом, вершина параболы имеет координаты:
. Таким образом, вершина параболы имеет координаты: 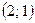 . Найдем площадь полученной фигуры:
. Найдем площадь полученной фигуры:
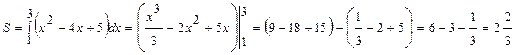 .
.
Ответ: 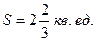
Задания для практической работы
1. Найдите площадь фигуры, ограниченной прямыми 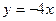 ,
, 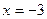 ,
, 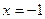 и осью абсцисс.
и осью абсцисс.
2. Найдите площадь фигуры, заключенной между осями координат и прямыми 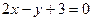 и
и 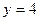 .
.
3. Найдите площадь фигуры, ограниченной ветвью гиперболы 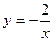 и прямыми
и прямыми 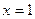 ,
,  .
.
4. Вычислите площадь фигуры, ограниченной параболой  , прямыми
, прямыми 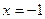 ,
, 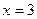 и осью абсцисс.
и осью абсцисс.
5. Найдите площадь фигуры, ограниченной параболой 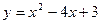 , осями координат и прямой
, осями координат и прямой 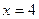 .
.
6. Найдите площадь фигуры, заключенной между прямыми 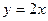 ,
, 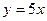 ,
, 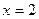 и
и 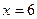 .
.
7. Найдите площадь фигуры, ограниченной указанными линиями 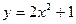 и
и 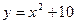 .
.
8. Найдите площадь фигуры, ограниченной указанными линиями 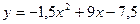 и
и 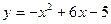 .
.
9. Найдите площадь фигуры, ограниченной указанными линиями 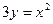 и
и 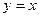 .
.
10. Найдите площадь фигуры, ограниченной указанными линиями 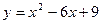 и
и 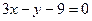 .
.
Контрольные вопросы:
1. По какой формуле вычисляется площадь фигуры, находящейся над осью 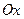 ?
?
2. По какой формуле вычисляется площадь фигуры прилегающей к оси 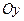 ?
?
3. По какой формуле вычисляется площадь фигуры, находящейся под осью 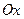 ?
?
4. По какой формуле вычисляется площадь фигуры расположенной по обе стороны оси 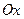 ?
?
5. По какой формуле вычисляется площадь фигуры, ограниченной двумя пересекающимися кривыми?
Рекомендуемая литература: 1.1 [с. 271-281], 1.2 [с. 205-212], 1.3 [с.395-395], 2.2 [с. 247-250].
Практическая работа №17
Тема: Нахождение области определения и вычисление частных значений для функции нескольких переменных
Цель: Формирование навыков нахождения области определения и вычисления частных значений для функции нескольких переменных
Время выполнения: 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Уравнение
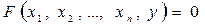 (неявная форма) (17.1)
(неявная форма) (17.1)
или
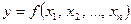 (явная форма) (17.2)
(явная форма) (17.2)
определяет переменную 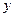 как функцию
как функцию 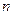 независимых переменных
независимых переменных 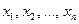 . Областью определения функции
. Областью определения функции 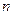 переменных является множество точек
переменных является множество точек 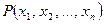
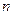 -мерного пространства, в которых функция принимает определенное действительное значение.
-мерного пространства, в которых функция принимает определенное действительное значение.
При 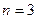 уравнение (17.1) определяет функцию трех переменных
уравнение (17.1) определяет функцию трех переменных
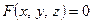 или
или 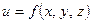 , (17.3)
, (17.3)
Областью определения, которой является множество точек 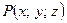 трехмерного пространства
трехмерного пространства 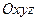 .
.
При 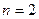 уравнение (17.1) определяет функцию двух переменных
уравнение (17.1) определяет функцию двух переменных
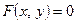 или
или 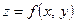 . (17.4)
. (17.4)
Частным значением 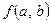 функции
функции 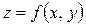 называется такое ее значение, которое соответствует системе значений
называется такое ее значение, которое соответствует системе значений 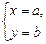 . (17.5)
. (17.5)
Примеры
Задание 1: Найти области определения функций:
1) 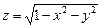 ; 2)
; 2) 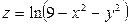 .
.
Решение: 1) Область определения функции состоит из всех точек 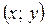 плоскости, для которых
плоскости, для которых 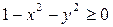 , то есть
, то есть 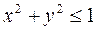 . Таким образом, искомая область есть круг с центром в начале координат и радиусом 1. она является замкнутой, так как включает свою границу – окружность
. Таким образом, искомая область есть круг с центром в начале координат и радиусом 1. она является замкнутой, так как включает свою границу – окружность 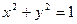 .
.
2) Так как логарифм определен только при положительных значениях аргумента, то 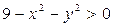 , откуда
, откуда 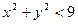 . Следовательно, областью определения данной функции служит внутренняя часть круга с центром в начале координат и радиусом 3. эта область открытая, поскольку она не включает свою границу – окружность
. Следовательно, областью определения данной функции служит внутренняя часть круга с центром в начале координат и радиусом 3. эта область открытая, поскольку она не включает свою границу – окружность  .
.
Задание 2: Найти частное значение функции 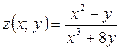 в точке
в точке 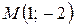 .
.
Решение: Подставляя в выражение функции значения 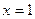 и
и 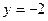 , получим
, получим 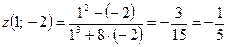 .
.
Задания для практической работы
1. На плоскости 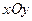 постройте область изменения переменных
постройте область изменения переменных 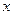 и
и 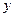 , заданные нижеследующими неравенствами. Укажите тип области.
, заданные нижеследующими неравенствами. Укажите тип области.
1) 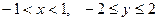 ; 2)
; 2) 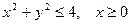 ;
;
3) 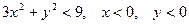 ; 4)
; 4) 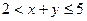 .
.
2. Найдите области определения функций и укажите, что будет являться областью определения:
1) 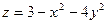 ; 2)
; 2) 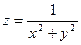 ; 3)
; 3) 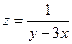 ;
;
4) 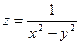 ; 5)
; 5) 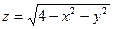 ; 6)
; 6) 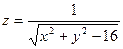 .
.
3. Вычислите частные значения функций:
1) 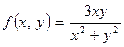 при
при 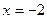 и
и 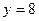 ;
;
2) 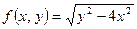 в точке
в точке 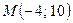 ;
;
3) 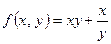 при
при 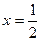 и
и 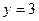 .
.
4. Дана функция 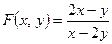 . Вычислите
. Вычислите 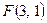 ,
, 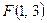 ,
, 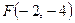 ,
, 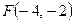 ,
, 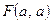 ,
, 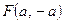 ,
, 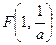 .
.
Контрольные вопросы:
1. Что называется функцией нескольких переменных?
2. Что называется областью определения функции 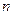 переменных?
переменных?
3. Что называется частным значением функции двух переменных?
4. Что называется границей области?
5. Какая область называется замкнутой, а какая открытой?
Рекомендуемая литература: 1.2 [с. 438-439], 2.1 [с. 192-204], 2.2 [с. 151-166].
Практическая работа №18



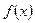 интегрируемая на промежутке
интегрируемая на промежутке 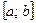 , если при любых разбиениях
, если при любых разбиениях 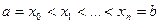 промежутка
промежутка 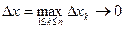 при произвольном выборе точек
при произвольном выборе точек 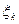 (где
(где 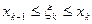 ), сумма
), сумма 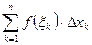 при
при 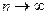 стремится к пределу
стремится к пределу 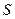 .
.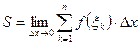 называют определенным интегралом от функции
называют определенным интегралом от функции 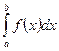 , то есть
, то есть 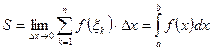 . (15.1)
. (15.1)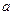 называется нижним пределом интеграла,
называется нижним пределом интеграла, 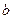 - верхним. Промежуток
- верхним. Промежуток 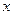 - переменной интегрирования.
- переменной интегрирования.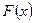 , служит формула Ньютона – Лейбница:
, служит формула Ньютона – Лейбница: 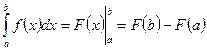 . (15.2). То есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
. (15.2). То есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.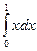 ; 2)
; 2) 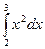 ; 3)
; 3) 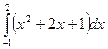 .
.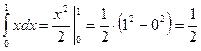 ; 2)
; 2) 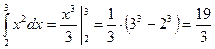 ;
;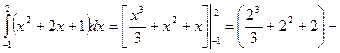
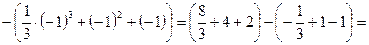
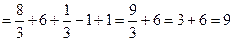
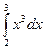 ; 2)
; 2) 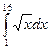 ; 3)
; 3) 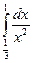 ; 4)
; 4) 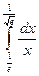 ; 5)
; 5) 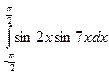
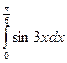 7)
7) 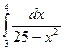 ; 8)
; 8) 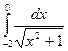 ; 9)
; 9) 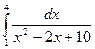 ;
;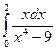 ; 11)
; 11) 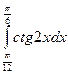 ; 12)
; 12) 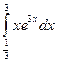 ; 13)
; 13) 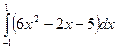 .
.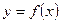 , осью
, осью  и двумя прямыми
и двумя прямыми 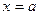 и
и 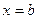 , где
, где 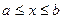 ,
, 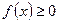 (рис.2).
(рис.2).
 и высотой
и высотой 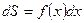 , то, интегрируя это равенство в пределах от
, то, интегрируя это равенство в пределах от 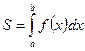 .
.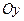 так, что
так, что 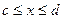 ,
, 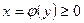 (рис.3), то дифференциал переменной площади
(рис.3), то дифференциал переменной площади 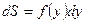 , откуда
, откуда 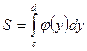 .
.

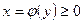

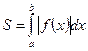 .
.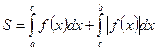 .
.
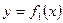 и
и 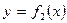 , прямыми
, прямыми 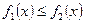 (рис. 6) Тогда ее площадь находится по формуле
(рис. 6) Тогда ее площадь находится по формуле 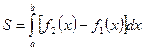 .
.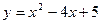 ,
, 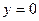 ,
, 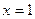 и
и 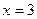 (рис. 7).
(рис. 7).
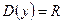 ; график – парабола, ветви направлены вверх.
; график – парабола, ветви направлены вверх.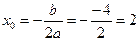 , отсюда следует, что
, отсюда следует, что 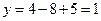 . Таким образом, вершина параболы имеет координаты:
. Таким образом, вершина параболы имеет координаты: 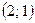 . Найдем площадь полученной фигуры:
. Найдем площадь полученной фигуры: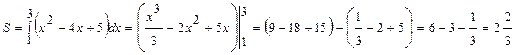 .
.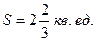
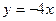 ,
, 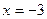 ,
, 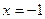 и осью абсцисс.
и осью абсцисс.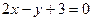 и
и 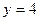 .
.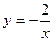 и прямыми
и прямыми  .
. , прямыми
, прямыми 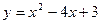 , осями координат и прямой
, осями координат и прямой 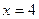 .
.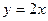 ,
, 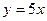 ,
, 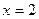 и
и 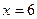 .
.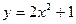 и
и 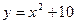 .
.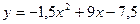 и
и 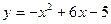 .
.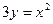 и
и 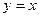 .
.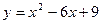 и
и 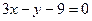 .
.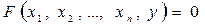 (неявная форма) (17.1)
(неявная форма) (17.1)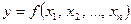 (явная форма) (17.2)
(явная форма) (17.2)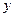 как функцию
как функцию 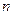 независимых переменных
независимых переменных 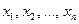 . Областью определения функции
. Областью определения функции 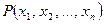
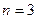 уравнение (17.1) определяет функцию трех переменных
уравнение (17.1) определяет функцию трех переменных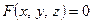 или
или 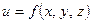 , (17.3)
, (17.3)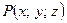 трехмерного пространства
трехмерного пространства 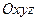 .
.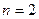 уравнение (17.1) определяет функцию двух переменных
уравнение (17.1) определяет функцию двух переменных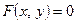 или
или 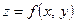 . (17.4)
. (17.4)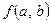 функции
функции 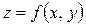 называется такое ее значение, которое соответствует системе значений
называется такое ее значение, которое соответствует системе значений 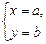 . (17.5)
. (17.5)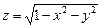 ; 2)
; 2) 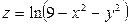 .
. плоскости, для которых
плоскости, для которых 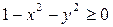 , то есть
, то есть 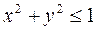 . Таким образом, искомая область есть круг с центром в начале координат и радиусом 1. она является замкнутой, так как включает свою границу – окружность
. Таким образом, искомая область есть круг с центром в начале координат и радиусом 1. она является замкнутой, так как включает свою границу – окружность 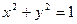 .
.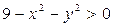 , откуда
, откуда 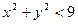 . Следовательно, областью определения данной функции служит внутренняя часть круга с центром в начале координат и радиусом 3. эта область открытая, поскольку она не включает свою границу – окружность
. Следовательно, областью определения данной функции служит внутренняя часть круга с центром в начале координат и радиусом 3. эта область открытая, поскольку она не включает свою границу – окружность  .
.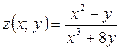 в точке
в точке 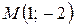 .
.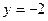 , получим
, получим 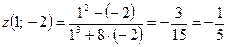 .
. постройте область изменения переменных
постройте область изменения переменных 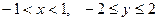 ; 2)
; 2) 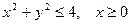 ;
;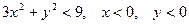 ; 4)
; 4) 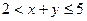 .
.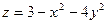 ; 2)
; 2) 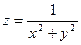 ; 3)
; 3) 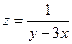 ;
;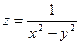 ; 5)
; 5) 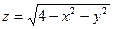 ; 6)
; 6) 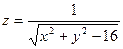 .
.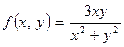 при
при 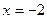 и
и 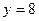 ;
;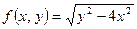 в точке
в точке 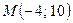 ;
;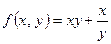 при
при 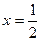 и
и 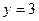 .
.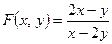 . Вычислите
. Вычислите 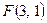 ,
, 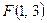 ,
, 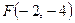 ,
, 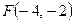 ,
, 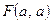 ,
, 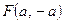 ,
, 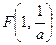 .
.


