Пусть прямые l 1 и l 2 заданы общими уравнениями:
А 1 х + В 1 у + С 1 = 0,
А 2 х + В 2 у + С 2 = 0.
Нормальные векторы этих прямых: 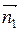 = (А 1; В 1) и
= (А 1; В 1) и 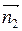 = (А 2; В 2).
= (А 2; В 2).
а) Прямая l 1 параллельна l 2 тогда и только тогда, когда векторы 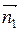 и
и 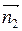 коллинеарны, их одноименные координаты пропорциональны. Значит, условие
коллинеарны, их одноименные координаты пропорциональны. Значит, условие
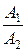 =
= 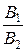 ≠
≠ 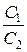
является условием параллельности прямых.
б) Если выполняется условие
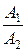 =
= 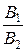 =
= 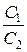 ,
,
то прямые l 1 и l 2 совпадают.
в) Если векторы 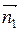 и
и 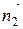 некомпланарны
некомпланарны
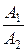 ≠
≠  ,
,
то прямые l 1 и l 2 пересекаются. Точку пересечения прямых находим, решая систему уравнений
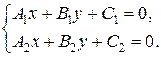
Угол φ между прямыми l 1 и l 2 определяется по формуле
cosφ =  =
= 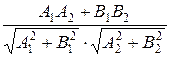 .
.
д) Если прямые l 1 и l 2 взаимно перпендикулярны, то их нормальные векторы 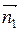 и
и 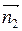 также взаимно перпендикулярны и поэтому их скалярное произведение равно нулю:
также взаимно перпендикулярны и поэтому их скалярное произведение равно нулю:
А 1 А 2 + В 1 В 2 = 0.
Если прямые заданы каноническими уравнениями
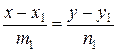 ,
, 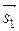 = (т 1; п 1);
= (т 1; п 1);
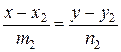 ,
, 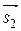 = (т 2; п 2),
= (т 2; п 2),
то
а) 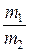 =
= 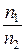
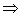
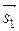 ↑↓
↑↓ 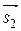
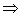 l 1 || l 2;
l 1 || l 2;
б) т 1 т 2 + п 1 п 2 = 0 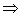
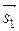
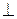
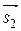
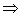 l 1
l 1 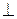 l 2;
l 2;
в) cosφ = 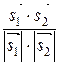 =
=  .
.
Пусть прямые l 1 и l 2 заданы уравнениями с угловыми коэффициентами:
у = k 1 х + b 1,
у = k х + b 2.
Тогда
а) k 1 = k 2 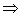 l 1 || l 2;
l 1 || l 2;
б) k 1 = 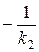
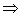 l 1
l 1 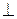 l 2;
l 2;
в) tgφ =  .
.
Расстояние d от точки М 0(х 0, у 0) до прямой l, заданной общим уравнением Ах + Ву + С = 0, находится по формуле
d = 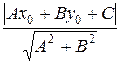 .
.
Пример 1. Даны точки М (2; 3) и N (–1; 0). Составить уравнение прямой, проходящей через точку М перпендикулярно отрезку MN.
Решение
Найдем координаты вектора 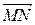 :
:
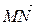 = (хN – xM; yN – yM) = (–1 – 2; 0 – 3) = (–3; –3).
= (хN – xM; yN – yM) = (–1 – 2; 0 – 3) = (–3; –3).
По условию вектор 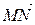 является нормальным вектором искомой прямой.
является нормальным вектором искомой прямой.
Составим уравнение прямой, проходящей через заданную точку М (2; 3) с заданным нормальным вектором 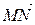 = (–3; –3):
= (–3; –3):
–3(х – 2) –3(у –3) = 0
или
х + у – 5 = 0 – уравнение искомой прямой.
Пример 2. Определить угловой коэффициент k и отрезок b, отсекаемый на оси ординат прямой 2 х + 5 у – 10 = 0.
Решение
Разрешив уравнение 2 х + 5 у – 10 = 0 относительно у, получим:
у = – 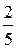 х + 2.
х + 2.
Сравнивая это уравнение с уравнением у = kх + b, находим k = 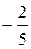 ,. b = 2.
,. b = 2.
Пример 3. Найти отрезки, отсекаемые на осях координат прямой
7 х + 2 у – 14 = 0.
Решение
Разделим обе части уравнения 7 х + 2 у – 14 = 0 на 14 и перенесем свободный член в правую часть:
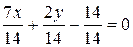 ,
,
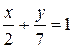 .
.
Сравнивая полученные уравнения с уравнением в отрезках по осям 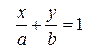 , находим а = 2, b = 7.
, находим а = 2, b = 7.
Пример 4. Написать уравнение прямой, проходящей через точку М (–2, 3) параллельно биссектрисе второго координатного угла.
Решение
Искомая прямая, как и биссектриса второго координатного угла, образует с положительным направлением оси Ох угол φ = 135°, поэтому k = tg135° = – 1. Так как точка М дана, то x 0 = – 2, y 0 = 3. Тогда уравнение y – y 0 = k (x – x 0) примет вид
у – 3 = (– 1)∙(х – (– 2)), у – 3 = – х + 2
или
х + у – 1 = 0.
Пример 5. Точки А (3; 5), В (– 1; 3), С (1; – 3) являются вершинами треугольника. Составить уравнение высоты треугольника, проведенной из вершины В.
Решение
Построим данный треугольник (рисунок 7). На высоте возьмем произвольную точку М (х; у) и рассмотрим вектор 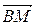 = (х + 1; у – 3), который является перпендикулярным вектору
= (х + 1; у – 3), который является перпендикулярным вектору 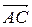 = (1 – 3; – 3 – 5) = (– 2; – 8). Значит, их скалярное произведение равно нулю:
= (1 – 3; – 3 – 5) = (– 2; – 8). Значит, их скалярное произведение равно нулю: 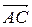 ∙
∙ 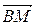 = 0. В координатной форме имеем
= 0. В координатной форме имеем
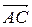 ∙
∙ 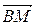 = – 2∙(х + 1) – 8∙(у – 3) = 0,
= – 2∙(х + 1) – 8∙(у – 3) = 0,
или
(х + 1) + 4∙(у – 3) = 0,
Х + 4 у – 11 = 0 – уравнение высоты BМ.
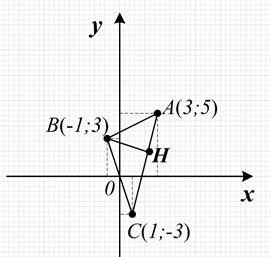
Рисунок 7 – Треугольник АВС
Пример 6. Даны вершина С (– 1; 3) прямого угла равнобедренного прямоугольного треугольника и уравнение его гипотенузы 3 х – 4 у – 12 = 0. Составить уравнения катетов.
Решение
Из уравнения гипотенузы выразим у и найдем ее угловой коэффициент:
3 х – 4 у – 12 = 0,
– 4 у = – 3 х + 12,
у = 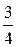 х – 3.
х – 3.
Следовательно, k 1 = 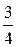 .
.
Катеты равнобедренного прямоугольного треугольника наклонены к гипотенузе под углом 45°. По формуле tgφ = 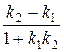 найдем угловые коэффициенты катетов:
найдем угловые коэффициенты катетов:
tg45° = 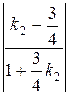 ,
,
±1 = 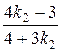 .
.
Если 1 = 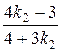 , то k 2 = 7.
, то k 2 = 7.
Если – 1 = 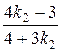 , то k 2 = –
, то k 2 = – 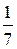 .
.
Зная координаты точки С (– 1; 3), принадлежащей двум катетам, получим их уравнения:
у – 3 = 7(х + 1), 7 х – у + 10 = 0.
у – 3 = – 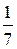 (х + 1), х + 7 у – 20 = 0.
(х + 1), х + 7 у – 20 = 0.
Пример 7. Найти уравнения прямых, которые параллельны прямой 12 х + 5 у – 7 = 0 и удалены от нее на расстояние равное трем.
Решение
Для любой точки прямой М (х; у) не лежащей на прямой 12 х + 5 у – 7 = 0, по формуле d = 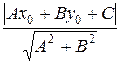 должно выполняться равенство
должно выполняться равенство
3 = 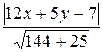 ,
,
или
|12 х + 5 у – 7| = 3∙13,
|12 х + 5 у – 7| = 39.
Следовательно,
12 х + 5 у – 7 = 39 или 12 х + 5 у – 7 = – 39.
Таким образом, получим уравнения прямых
12 х + 5 у – 46 = 0 и 12 х + 5 у + 32 = 0.
Пример 8. Даны уравнения двух смежных сторон АВ и АD параллелограмма и точка N пересечения его диагоналей. Найти уравнения двух других сторон параллелограмма, если N (3; 3), х + у – 1 = 0 (АВ), 3 х – у + 5 = 0 (АD).
Решение
Найдем координаты точки пересечения прямых АВ и АD, решив систему уравнений
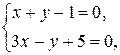
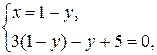
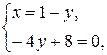
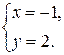
Получили точку А (– 1; 2).
Найдем координаты точки С, применив формулы деления отрезка пополам (так как точка N – середина диагонали АС).
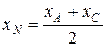 ,
, 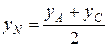 .
.
Таким образом, имеем
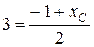 ,
, 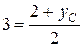 ,
,
откуда хС = 7, уС = 4, то есть С (7; 4).
Так как четырехугольник АВСD – параллелограмм, то АВ || СD и AD || CB и 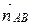 ↑↓
↑↓ 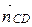 ,
, 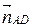 ↑↓
↑↓ 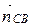 . Значит, можно считать, что
. Значит, можно считать, что 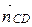 =
= 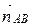 = (1; 1),
= (1; 1), 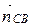 =
= 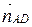 = (3; – 1). Запишем уравнения сторон СD и СВ, используя уравнение (1.1). Имеем
= (3; – 1). Запишем уравнения сторон СD и СВ, используя уравнение (1.1). Имеем
3(х – 7) – (у – 4) = 0, 3 х – у – 17 = 0 (СВ),
(х – 7) + (у – 4) = 0, х + у – 11 = 0 (СD).
Вопросы для самопроверки
1 Записать общее уравнение прямой на плоскости.
2 Каков геометрический смысл коэффициентов при х и у в общем уравнении прямой?
3 Записать уравнение прямой на плоскости, проходящей через точку М 0(х 0; у 0) перпендикулярно вектору 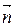 = (А; В).
= (А; В).
4 Записать каноническое уравнение прямой на плоскости и указать геометрический смысл входящих в него параметров.
5 Записать параметрические уравнения прямой на плоскости.
6 Записать уравнение прямой с угловым коэффициентом и указать геометрический смысл входящих в него параметров.
7 Записать уравнение прямой, проходящей через точку М 0(х 0; у 0) и образующей с осью абсцисс угол, тангенс которого равен k.
8 Записать уравнение прямой, проходящей через точки М 1(х 1; у 1) и М 2(х 2; у 2).
9 Записать уравнение прямой в отрезках по осям и указать геометрический смысл входящих в него параметров.
10 Записать формулы, по которым можно найти угол φ между прямыми.
11 Записать условие параллельности и условие перпендикулярности двух прямых, заданных:
а) общими уравнениями;
б) каноническими уравнениями;
в) уравнениями с угловыми коэффициентами.
12 Чему равно расстояние от точки М 0(х 0; у 0) до прямой Ах + Ву + С = 0?
Задачи для самостоятельного решения
1 Составить уравнение прямой, проходящей через точку М (– 2; 2) параллельно вектору:
а) 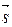 = (– 1; 1);
= (– 1; 1);
б) 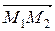 , если М 1(2; – 5), М 2(3; 1).
, если М 1(2; – 5), М 2(3; 1).
(Ответ: а) х + у = 0; б) 6 х – у + 14 = 0)
2 Найти уравнение прямой, проходящей через точку М (1; 2) с нормальным вектором 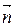 = (3; – 4). (Ответ: 3 х – 4 у + 5= 0)
= (3; – 4). (Ответ: 3 х – 4 у + 5= 0)
3 При каком значении С точка М (3;– 2) принадлежит прямой 2 х + 5 у + С = 0. (Ответ: С = 4)
4 Задана прямая 2 х + 3 у + 4 = 0. Составить уравнение прямой, проходящей через точку М (2; 1):
а) параллельно данной прямой;
б) перпендикулярно данной прямой;
в) под углом 45° к данной прямой.
(Ответ: а) 2 х + 3 у – 7 = 0; б) 3 х – 2 у – 4 = 0; в) х – 5 у + 3 = 0, 5 х + у – 11 = 0)
5 Найти уравнение прямой, проходящей через точку М (– 4; 10) и отсекающей отрезки равной длины на осях координат. (Ответ: х + у – 6 = 0)
6 Дан треугольник с вершинами Р (3; 1), Q (– 3; – 1), R (5; 12). Найти уравнение медианы, проведенной из вершины R, и вычислить ее длину. (Ответ: 12 х + 5 у = 0, d = 13)
7 Даны две вершины А (– 2; 1) и В (3; – 4) треугольника и точка N (5; – 1) пересечения его высот. Найти уравнения всех сторон треугольника. (Ответ: х + у + 1 = 0, 7 х – 2 у – 29 = 0, 2 х + 3 у + 1 = 0)
8 Найти уравнение прямой, проходящей через точку А (1; – 2) и точку пересечения прямых 2 х + 3 у – 4 = 0 и 3 х – 5 у + 13 = 0. (Ответ: 2 х + у = 0)
9 Найти проекцию точки А (– 8; 12) на прямую, проходящую через точки М 1(2; – 3) и М 2(– 5; 1). (Ответ: (– 12; 5))
10 Найти точку В, симметричную точке А (8; 12) относительно прямой х – 2 у + 6 = 0. (Ответ: В (12; 4))
11 Через точку А (2; 5) провести прямые, которые находятся на одинаковом расстоянии от точек М 1(– 1; 2) и М 2(5; 4). (Ответ: х – 2 = 0, х – 3 у + 13 = 0)
12 Найти угол между прямыми:
а) х + 5 у – 3 = 0, 2 х – 3 у + 4 = 0;
б) х + 2 у – 3 = 0, у = – 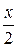 –
– 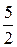 ;
;
в) у = 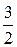 х + 1, у =
х + 1, у = 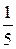 х – 3.
х – 3.
(Ответ: а) 45°; б) 0°; в) 45°)
13 Определить, при каком значении параметра α прямые
(α – 1) х – 2α у + 5 = 0 и α х + 4α у – 6 = 0:
а) параллельны;
б) совпадают;
в) взаимно перпендикулярны.
(Ответ: а) α = 2; б) ни при каком α; в) α = 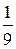 )
)
14 Две стороны квадрата лежат на прямых, заданных уравнениями 5 х – 12 у – 65 = 0 и 5 х – 12 у + 26 = 0. Найти площадь квадрата. (Ответ: 49)
15 Доказать, что прямые 3 х – 4 у + 10 = 0 и 6 х – 8 у + 15 = 0 и найти расстояние между ними. (Ответ: 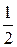 )
)
Линии второго порядка
Окружность
Окружностью называют множество всех точек плоскости, равноудаленных от некоторой фиксированной точки, называемой центром окружности.
Если R – радиус окружности, а точка М (х 0; у 0) – центр окружности, то ее уравнение имеет вид
(х – х 0)2 + (у – у 0)2 = R 2.
Если центр окружности совпадает с началом координат, то ее уравнение записывается в виде
х 2 + у 2 = R 2.
Эллипс
Эллипсом называют множество всех точек плоскости, для которых сумма расстояний от двух данных точек F 1 и F 2, называемых фокусами, есть величина постоянная, равная 2 а, и большая, чем расстояние между фокусами 2 с (2 а > 2 с).
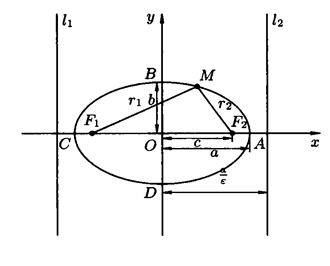
Рисунок 8 – Эллипс
Каноническое уравнение эллипса:
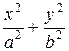 = 1.
= 1.
Начало координат О (0; 0) является центром симметрии эллипса, а оси координат – осями симметрии эллипса. Точки А (а; 0), С (– а; 0), В (0; b), D (0; – b) называются вершинами эллипса (рисунок 8).
b 2 = а 2 – с 2, а = ОА – большая полуось, b = ОВ – малая полуось. Координаты фокусов F 1(– c; 0), F 2(c; 0).
Отношение
ε = 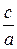 < 1
< 1
называется эксцентриситетом эллипса.
Прямые х = ± 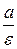 называются директрисами эллипса.
называются директрисами эллипса.
Если а < b, то фокусы эллипса находятся на оси Оу, с 2 = b 2 – а 2, ε = 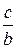 .
.
Гипербола
Гиперболой называют множество всех точек плоскости, для которых модуль разности расстояний от двух данных точек F 1 и F 2, называемых фокусами, есть величина постоянная, равная 2 а, и меньшая, чем расстояние между фокусами 2 с (2 а < 2 с).
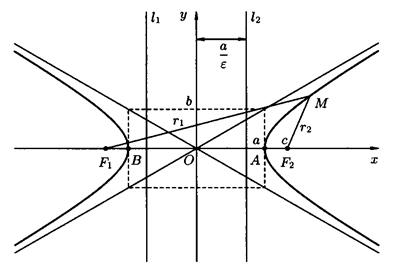
Рисунок 9 – Гипербола
Каноническое уравнение гиперболы:
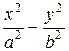 = 1.
= 1.
Начало координат О (0; 0) является центром симметрии гиперболы, а оси координат – осями гиперболы. Точки А (а; 0), В (– а; 0) называются вершинами гиперболы (рисунок 9).
b 2 = с 2 – а 2, а – действительная полуось, b – мнимая полуось. Координаты фокусов F 1(– c; 0), F 2(c; 0).
Отношение
ε = 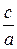 > 1
> 1
называется эксцентриситетом гиперболы.
Прямые у = ± 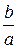 х называются асимптотами гиперболы.
х называются асимптотами гиперболы.
Гипербола, у которой a = b, называется равносторонней.
Уравнение
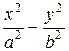 = – 1
= – 1
также является уравнением гиперболы, но действительной осью этой гиперболы служит отрезок оси Оу длиной 2 b.
Парабола
Параболой называют множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки F, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
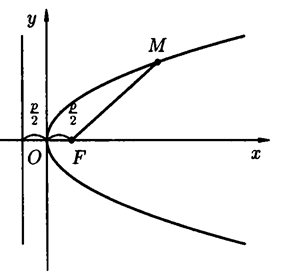
Рисунок 10 – Парабола
Каноническое уравнение параболы, симметричной относительно оси Ох и проходящей через начало координат, имеет вид
у 2 = 2 рх,
где р – расстояние от фокуса параболы F (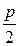 ; 0) до ее директрисы х = –
; 0) до ее директрисы х = – 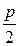 (рисунок 10).
(рисунок 10).
Каноническое уравнение параболы, симметричной относительно оси Оу с вершиной в начале координат, имеет вид
х 2 = 2 ру.
В этом случае F (0; 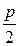 ) – фокус, у = –
) – фокус, у = – 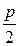 – уравнение директрисы.
– уравнение директрисы.
Пример 1. Составить уравнение окружности, если точки М 1(3; 2), М 2(– 1; 6) – концы диаметра окружности.
Решение
Найдем координаты центра окружности по формулам деления отрезка пополам:
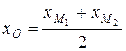 =
= 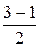 = 1,
= 1,
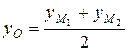 =
= 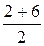 = 4.
= 4.
Вычислим радиус окружности:
ОМ 1 = R = 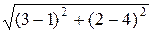 =
= 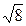 = 2
= 2 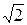 .
.
Тогда уравнение окружности:
(х – 1)2 + (у – 4)2 = 8.
Пример 2. Составить каноническое уравнение эллипса, если известно, что его большая полуось а = 12, а эксцентриситет ε = 0,5.
Решение
Известно, что ε = 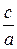 . Следовательно,
. Следовательно,
с = а ε = 12∙0,5 = 6.
Используя соотношение b 2 = а 2 – с 2, получим
b 2 = 144 – 36 = 108.
Таким образом, искомое уравнение эллипса имеет вид
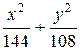 = 1.
= 1.
Пример 3. Составить уравнение гиперболы, если известно, что она проходит через точку М (9; 8), а асимптоты заданы уравнениями у = ± 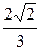 х. Найти эксцентриситет гиперболы.
х. Найти эксцентриситет гиперболы.
Решение
Из уравнений асимптот гиперболы находим 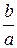 =
= 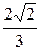 , или b =
, или b = 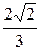 а.
а.
Подставив в каноническое уравнение гиперболы полученное выражение для b, имеем
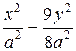 = 1.
= 1.
Точка М (9; 8) принадлежит гиперболе, следовательно, ее координаты удовлетворяют уравнению гиперболы. Значит
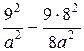 = 1,
= 1,
81 – 72 = а 2,
а 2 = 9, а = 3.
Тогда b = 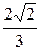 а =
а = 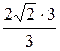 =
= 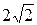 . Искомое уравнение гиперболы имеет вид
. Искомое уравнение гиперболы имеет вид
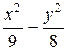 = 1.
= 1.
Найдем эксцентриситет гиперболы:
ε = 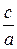 =
= 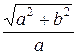 =
= 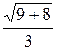 =
= 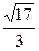 .
.
Пример 4. Составить уравнение параболы, если известно, что:
а) фокус параболы F (5; 0), а ее директрисой является ось ординат;
б) парабола симметрична относительно оси Оу и проходит через точки О (0; 0) и М (6; – 2).
Решение
а) По условию р = 5 и вершина параболы имеет координаты (2,5; 0), то, используя уравнение у 2 = 2 р (х – х 0), получим
у 2 = 10(х – 2,5),
у 2 = 10 х – 25.
б) Запишем уравнение параболы в общем виде: х 2 = 2 ру.
Точка М (6; – 2) удовлетворяет уравнению параболы, то есть
36 = 2 р ∙(– 2),
– 4 р = 36,
р = – 9.
Тогда уравнение параболы имеет вид
х 2 = – 18 у.
Вопросы для самопроверки
1 Какая линия называется эллипсом? Какие точки называются фокусами эллипса?
2 Записать каноническое уравнение эллипса.
3 Для эллипса, заданного каноническим уравнением 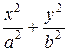 = 1, указать оси симметрии и вершины.
= 1, указать оси симметрии и вершины.
4 Какая ось эллипса называется большой осью и какая – малой?
5 Пусть 2 а и 2 b – соответственно большая и малая оси эллипса, а 2 с – расстояние между его фокусами. Какова зависимость между а, b и с?
6 Какая линия называется гиперболой? Какие точки называются фокусами гиперболы?
7 Записать каноническое уравнение гиперболы.
8 Для гиперболы, заданной каноническим уравнением 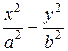 = 1, указать оси симметрии и вершины.
= 1, указать оси симметрии и вершины.
9 Указать вершины гиперболы, заданной каноническим уравнением 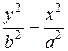 = 1.
= 1.
10 Что является действительной осью гиперболы 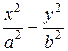 = 1?
= 1?
11 Что является мнимой осью гиперболы 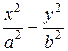 = 1?
= 1?
12 Пусть 2 а и 2 b – соответственно действительная и мнимая оси гиперболы, а 2 с – расстояние между ее фокусами. Какова зависимость между а, b и с?
13 Записать уравнения асимптот гиперболы 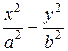 = 1.
= 1.
14 Какая линия называется параболой? Какая точка называется фокусом параболы и какая прямая – директрисой, заданной уравнением у 2 = 2 рх?
15 Записать каноническое уравнение параболы.
16 Какая точка называется вершиной параболы?
17 Что называется эксцентриситетом эллипса?
18 Чему равен эксцентриситет ε эллипса, заданного уравнением 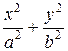 = 1, где а > b?
= 1, где а > b?
19 Что называется эксцентриситетом гиперболы?
20 Чему равен эксцентриситет ε гиперболы, заданной уравнением 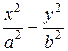 = 1?
= 1?
Задачи для самостоятельного решения
1 Составить уравнение окружности, которая имеет центр в точке М (2; 3) и касается прямой х – 2 у + 1 = 0. (Ответ: (х – 2)2 + (у – 3)2 = 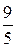 )
)
2 Составить уравнение окружности, которая проходит через точки А (5; 0) и В (1; 4), если ее центр лежит на прямой х + у – 3 = 0.
(Ответ: (х – 2)2 + (у – 1)2 = 10)
3 Составить уравнение хорды окружности х 2 + у 2 = 49, которая делится точкой А (1; 2) пополам. (Ответ: х + 2 у – 5 = 0)
4 Составить каноническое уравнение эллипса, проходящего через точки М (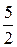 ;
; 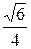 ) и N (–2;
) и N (–2; 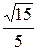 ). (Ответ:
). (Ответ: 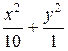 = 1)
= 1)
5 Составить уравнение геометрического множества точек плоскости, расстояние от которых до точки А (0; 1) в два раза меньше расстояния до прямой у – 4 = 0. (Ответ: 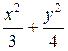 = 1)
= 1)
6 Составить каноническое уравнение эллипса, если известно, что малая полуось равна 6, а расстояние между фокусами равно 16. (Ответ: 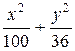 = 1)
= 1)
7 Эллипс касается оси абсцисс в вершине А (4; 0) и оси ординат в вершине В (0; – 3).Составить уравнение эллипса. (Ответ: 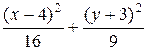 = 1)
= 1)
8 Найти эксцентриситет эллипса, если известно, что:
а) большая ось втрое больше малой;
б) оси относятся как 5:3.
(Ответ: а) 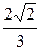 ; б) 0,8)
; б) 0,8)
9 Составить каноническое уравнение эллипса, если известно, что:
а) малая полуось равна 6, эксцентриситет равен 0,8;
б) расстояние между фокусами равно 6, эксцентриситет равен 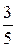 ;
;
в) сумма полуосей равна 10, расстояние между фокусами равно 4 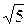 .
.
(Ответ: а) 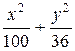 = 1; б)
= 1; б) 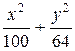 = 1; в)
= 1; в) 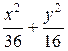 = 1)
= 1)
10 Составить каноническое уравнение гиперболы, действительная ось которой равна 48, а эксцентриситет равен 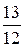 . (Ответ:
. (Ответ: 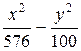 = 1)
= 1)
11 Составить уравнение гиперболы, проходящей через точку М (24; 5), если ее асимптоты заданы уравнениями у = ± 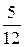 х. (Ответ:
х. (Ответ: 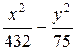 = 1)
= 1)
12 Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы – в вершинах эллипса 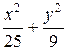 = 1. (Ответ:
= 1. (Ответ: 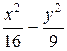 = 1)
= 1)
13 Найти уравнение параболы и ее директрисы, если известно, что парабола проходит через точку пересечения прямой х + у = 0 и окружности х 2 + у 2 – 4 х = 0 и симметрична относительно оси Оу. (Ответ: х 2 = – 2 у; у = 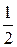 )
)
14 Составить уравнение параболы, если известно, что ее фокус находится в точке пересечения прямой 4 х – 3 у – 4 = 0 с осью Ох. (Ответ: у 2 = 4 х)
15 Привести уравнения линий второго порядка к каноническому виду, определить их тип и расположение на плоскости:
а) 4 х 2 + 9 у 2 – 40 х + 36 у + 100 = 0;
б) 16 х 2 – 9 у 2 – 64 х – 18 у + 199 = 0;
в) 5 х 2 + 9 у 2 – 30 х + 18 у + 9 = 0;
г) 3 х 2 – 4 у 2 – 12 х + 24 = 0;
д) у 2 + 2 у + 4 х – 11 = 0.
(Ответ: а) 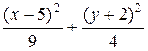 = 1 – эллипс; б)
= 1 – эллипс; б) 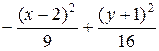 = 1 – гипербола; в)
= 1 – гипербола; в)  = 1 – эллипс; г)
= 1 – эллипс; г) 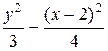 = 1 – гипербола; д) (у + 1)2 = – (х – 3) – парабола)
= 1 – гипербола; д) (у + 1)2 = – (х – 3) – парабола)



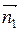 = (А 1; В 1) и
= (А 1; В 1) и 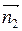 = (А 2; В 2).
= (А 2; В 2).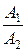 =
= 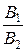 ≠
≠ 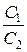
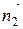 некомпланарны
некомпланарны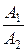 ≠
≠  ,
,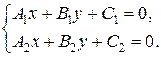
 =
= 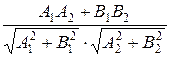 .
.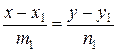 ,
, 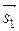 = (т 1; п 1);
= (т 1; п 1);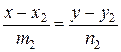 ,
, 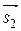 = (т 2; п 2),
= (т 2; п 2),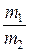 =
= 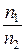
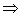
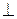
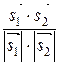 =
=  .
.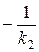
 .
.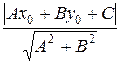 .
.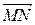 :
: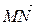 = (хN – xM; yN – yM) = (–1 – 2; 0 – 3) = (–3; –3).
= (хN – xM; yN – yM) = (–1 – 2; 0 – 3) = (–3; –3).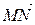 является нормальным вектором искомой прямой.
является нормальным вектором искомой прямой.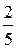 х + 2.
х + 2.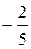 ,. b = 2.
,. b = 2.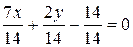 ,
,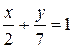 .
.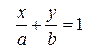 , находим а = 2, b = 7.
, находим а = 2, b = 7.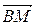 = (х + 1; у – 3), который является перпендикулярным вектору
= (х + 1; у – 3), который является перпендикулярным вектору 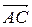 = (1 – 3; – 3 – 5) = (– 2; – 8). Значит, их скалярное произведение равно нулю:
= (1 – 3; – 3 – 5) = (– 2; – 8). Значит, их скалярное произведение равно нулю: 
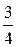 х – 3.
х – 3.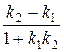 найдем угловые коэффициенты катетов:
найдем угловые коэффициенты катетов: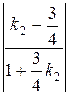 ,
,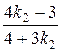 .
.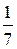 .
.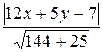 ,
,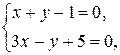
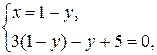
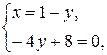
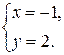
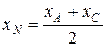 ,
, 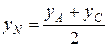 .
.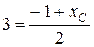 ,
, 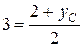 ,
,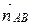 ↑↓
↑↓ 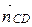 ,
, 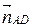 ↑↓
↑↓ 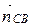 . Значит, можно считать, что
. Значит, можно считать, что 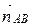 = (1; 1),
= (1; 1), 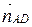 = (3; – 1). Запишем уравнения сторон СD и СВ, используя уравнение (1.1). Имеем
= (3; – 1). Запишем уравнения сторон СD и СВ, используя уравнение (1.1). Имеем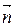 = (А; В).
= (А; В).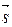 = (– 1; 1);
= (– 1; 1);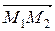 , если М 1(2; – 5), М 2(3; 1).
, если М 1(2; – 5), М 2(3; 1).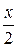 –
– 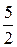 ;
;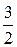 х + 1, у =
х + 1, у = 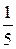 х – 3.
х – 3.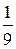 )
)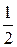 )
)
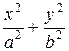 = 1.
= 1.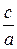 < 1
< 1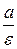 называются директрисами эллипса.
называются директрисами эллипса.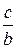 .
.
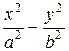 = 1.
= 1.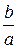 х называются асимптотами гиперболы.
х называются асимптотами гиперболы.
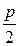 ; 0) до ее директрисы х = –
; 0) до ее директрисы х = – 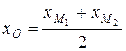 =
= 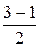 = 1,
= 1,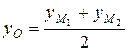 =
= 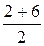 = 4.
= 4.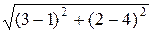 =
= 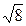 = 2
= 2 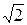 .
.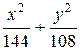 = 1.
= 1.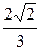 х. Найти эксцентриситет гиперболы.
х. Найти эксцентриситет гиперболы.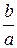 =
= 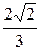 , или b =
, или b = 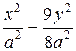 = 1.
= 1.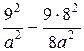 = 1,
= 1,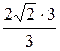 =
= 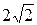 . Искомое уравнение гиперболы имеет вид
. Искомое уравнение гиперболы имеет вид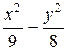 = 1.
= 1.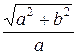 =
= 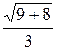 =
= 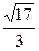 .
.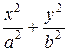 = 1, указать оси симметрии и вершины.
= 1, указать оси симметрии и вершины.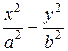 = 1, указать оси симметрии и вершины.
= 1, указать оси симметрии и вершины.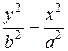 = 1.
= 1.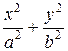 = 1, где а > b?
= 1, где а > b?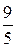 )
)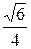 ) и N (–2;
) и N (–2; 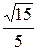 ). (Ответ:
). (Ответ: 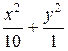 = 1)
= 1)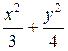 = 1)
= 1)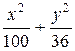 = 1)
= 1)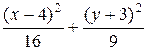 = 1)
= 1)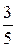 ;
;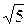 .
.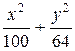 = 1; в)
= 1; в) 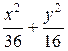 = 1)
= 1)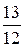 . (Ответ:
. (Ответ: 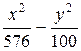 = 1)
= 1)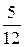 х. (Ответ:
х. (Ответ: 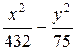 = 1)
= 1)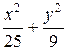 = 1. (Ответ:
= 1. (Ответ: 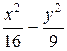 = 1)
= 1)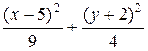 = 1 – эллипс; б)
= 1 – эллипс; б) 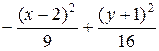 = 1 – гипербола; в)
= 1 – гипербола; в)  = 1 – эллипс; г)
= 1 – эллипс; г) 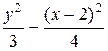 = 1 – гипербола; д) (у + 1)2 = – (х – 3) – парабола)
= 1 – гипербола; д) (у + 1)2 = – (х – 3) – парабола)


