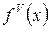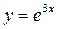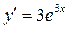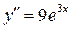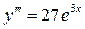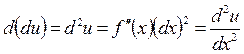Вопросы:
1. Понятие производной, ее геометрический и физический смысл.
2. Правила дифференцирования.
3. Производные высших порядков. Дифференциал функции.
1. Понятие производной 


 Пусть М – некоторая точка кривой γ
Пусть М – некоторая точка кривой γ
 Если
Если 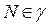 и
и  , то
, то
секущая 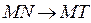 , если она
, если она

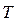 существует. Предельное положение
существует. Предельное положение
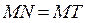 – касательная к γ в точке М.
– касательная к γ в точке М.
Пусть 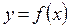 определена в некоторой точке х и ее окрестности. Дадим аргументы х приращение
определена в некоторой точке х и ее окрестности. Дадим аргументы х приращение 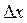 , при этом
, при этом 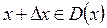 . Тогда функция получит приращение
. Тогда функция получит приращение 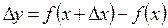 .
.
Опр.: Производной функции 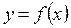 в точке х называется предел отношения приращения функции к приращению аргумента при стремлении к нулю, если это предел существует.
в точке х называется предел отношения приращения функции к приращению аргумента при стремлении к нулю, если это предел существует.
Обозначения 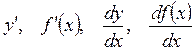
Итак, по определению
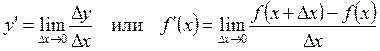 (*)
(*)
Процесс нахождения производной называется дифференцированием этой функции.
Функция называется дифференцируемой в некоторой точке х, если существует предел см. (*).
Непрерывность есть необходимое (но не достаточное) условие дифференцируемости функции.
Функция непрерывная в некоторой точке х может быть и не дифференцируемой в этой точке.
Пример:  в точке х = 0 не дифференцируема.
в точке х = 0 не дифференцируема.
Геометрический смысл производной
Секущая MN при 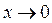 становится касательной
становится касательной  , т.е.
, т.е. 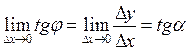
Т.е. производная функции  в точке х равна угловому коэффициенту касательной в точке
в точке х равна угловому коэффициенту касательной в точке 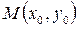 к кривой заданной уравнением
к кривой заданной уравнением 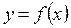 .
.
Физический смысл производной
Если за промежуток времени 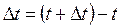 тело прошло путь
тело прошло путь  , то средняя скорость движения тела равна
, то средняя скорость движения тела равна
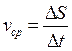
При 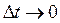 получим мгновенную скорость в t, т.е.
получим мгновенную скорость в t, т.е.

Правила дифференцирования
Схема вычисления производной:
1. Дать аргументу приращение 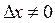 , найти значения функции
, найти значения функции 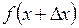 .
.
2. Найти приращение функции 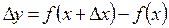 .
.
3. Составить отношение 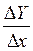
4. Найдем предел этого отношения при 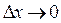 , т.е.
, т.е. 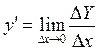 (если этот придел существует).
(если этот придел существует).
Пример: 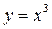
1. 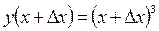
2. 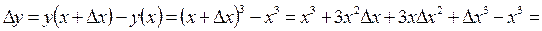
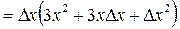
3. 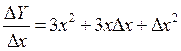
4. 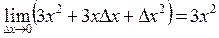
Т.о. 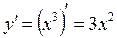 .
.
Можно доказать, что 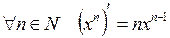 .
.
Правила дифференцирования:
1. 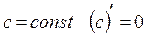
2. 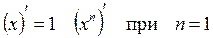
3. 
4. 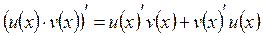
5. 
6. 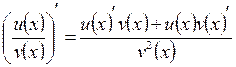
Таблица производных:
1. 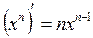
2. 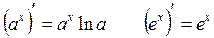
3. 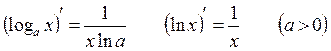
4. 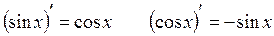
5. 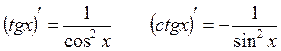
6. 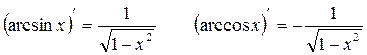
7. 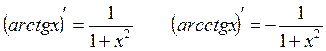
Производная сложной функции:
Теорема: Если 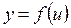 и
и 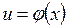 – дифференцируемы функции от своих аргументов, то производная сложной функции:
– дифференцируемы функции от своих аргументов, то производная сложной функции:
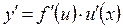
Действительно:
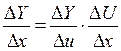
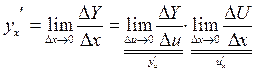
Пример:
1) 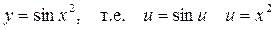
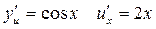 , получим
, получим 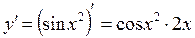
2) 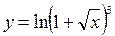

Производная обратной функции:
Дифференцируемая функция 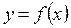 с производной
с производной 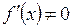 имеет однозначную непрерывную обратную функцию
имеет однозначную непрерывную обратную функцию  , причем обратная функция так же дифференцируема и справедлива формула:
, причем обратная функция так же дифференцируема и справедлива формула:

Пример:

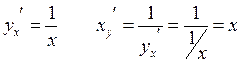
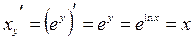
Дифференциал функции. Производные высших порядков
Опр.: Выражение 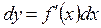 называется дифференциалом функции
называется дифференциалом функции  .
.
Он имеет следующие свойства:
1) 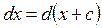
2) 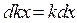
золотые свойства дифференциала, которые пригодятся при нахождении интегралов функции.
Опр.: Т.к. производная функции 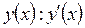 в свою очередь так же является функцией то ее можно продифференцировать. Производной n -го называется от производной (n –1)-го порядка.
в свою очередь так же является функцией то ее можно продифференцировать. Производной n -го называется от производной (n –1)-го порядка.
Обозначение:
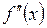 – 2-го порядка
– 2-го порядка
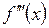 – 3-го порядка
– 3-го порядка
…….
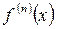 – n-го порядка
– n-го порядка
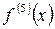 или
или 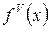
Пример: 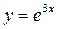
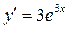
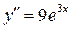
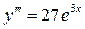

Аналогично определяются дифференциалы высших порядков:
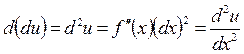






 Пусть М – некоторая точка кривой γ
Пусть М – некоторая точка кривой γ Если
Если 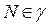 и
и  , то
, то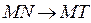 , если она
, если она
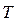 существует. Предельное положение
существует. Предельное положение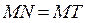 – касательная к γ в точке М.
– касательная к γ в точке М.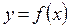 определена в некоторой точке х и ее окрестности. Дадим аргументы х приращение
определена в некоторой точке х и ее окрестности. Дадим аргументы х приращение 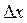 , при этом
, при этом 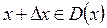 . Тогда функция получит приращение
. Тогда функция получит приращение 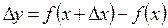 .
.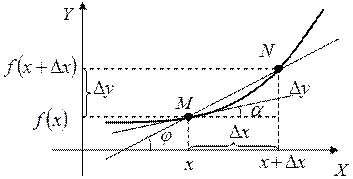
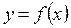 в точке х называется предел отношения приращения функции к приращению аргумента при стремлении к нулю, если это предел существует.
в точке х называется предел отношения приращения функции к приращению аргумента при стремлении к нулю, если это предел существует.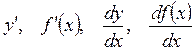
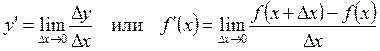 (*)
(*) в точке х = 0 не дифференцируема.
в точке х = 0 не дифференцируема.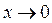 становится касательной
становится касательной  , т.е.
, т.е. 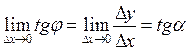
 в точке х равна угловому коэффициенту касательной в точке
в точке х равна угловому коэффициенту касательной в точке 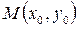 к кривой заданной уравнением
к кривой заданной уравнением 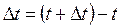 тело прошло путь
тело прошло путь  , то средняя скорость движения тела равна
, то средняя скорость движения тела равна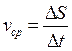
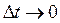 получим мгновенную скорость в t, т.е.
получим мгновенную скорость в t, т.е.
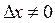 , найти значения функции
, найти значения функции 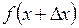 .
.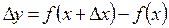 .
.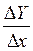
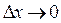 , т.е.
, т.е. 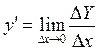 (если этот придел существует).
(если этот придел существует).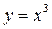
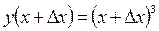
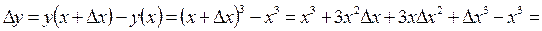
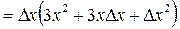
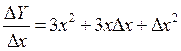
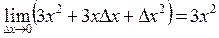
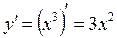 .
.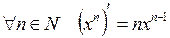 .
.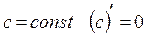
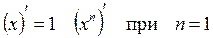

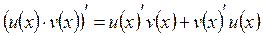

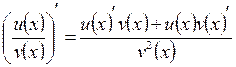
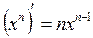
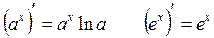
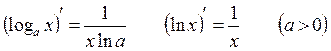
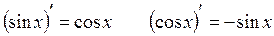
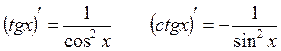
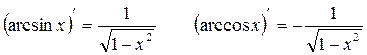
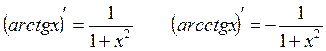
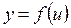 и
и 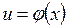 – дифференцируемы функции от своих аргументов, то производная сложной функции:
– дифференцируемы функции от своих аргументов, то производная сложной функции: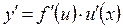
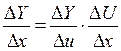
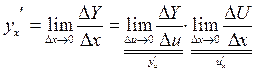
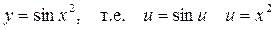
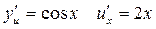 , получим
, получим 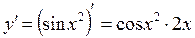
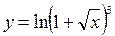

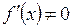 имеет однозначную непрерывную обратную функцию
имеет однозначную непрерывную обратную функцию  , причем обратная функция так же дифференцируема и справедлива формула:
, причем обратная функция так же дифференцируема и справедлива формула:

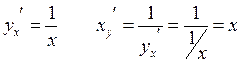
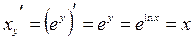
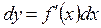 называется дифференциалом функции
называется дифференциалом функции 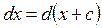
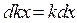
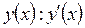 в свою очередь так же является функцией то ее можно продифференцировать. Производной n -го называется от производной (n –1)-го порядка.
в свою очередь так же является функцией то ее можно продифференцировать. Производной n -го называется от производной (n –1)-го порядка.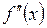 – 2-го порядка
– 2-го порядка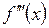 – 3-го порядка
– 3-го порядка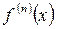 – n-го порядка
– n-го порядка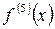 или
или