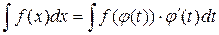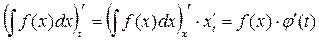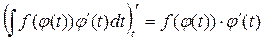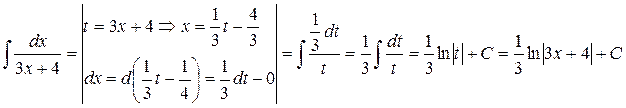Лекция 1. ФУНКЦИОНАЛЬНАЯ ВЗАИМОСВЯЗЬ
Вопросы:
1. Множества и операции над ними.
2. Понятие функции.
3. Уравнение прямой и взаимное расположение прямых на плоскости.
4. Уравнение плоскости.
5. Взаимное расположение прямой и плоскости в пространстве.
6. Кривые второго порядка.
Множества и операции над ними
Опр.: Множество – совокупность объектов, которые рассматриваются как единое целое.
Объекты, которые образуют множество называются элементами или точками этого множества.
Пример:
1) Множество студентов группы.
2) Множество предприятий страны.
3) Множество R.
Обозначение: 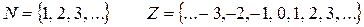

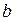
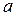
 Если
Если 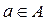


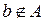
Опр.: Множество, не содержащее ни одного элемента называется пустым и обозначается Ø.
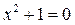
Множество действительных корней Ø.

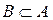
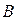

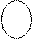 B является подмножеством А,
B является подмножеством А,
если 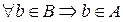
Опр.: Два множества А и В называются равными, если они состоят из одних и тех же элементов.
 .
.
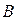
 Операции над множествами:
Операции над множествами:


 1. Объединение
1. Объединение 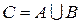
каждый элемент 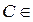 хотя бы
хотя бы
одному из множеств А или В.
2. Пересечением 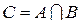 каждый элемент
каждый элемент 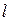 принадлежащий и множеству А, и множеству В.
принадлежащий и множеству А, и множеству В.
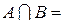 Ø
Ø
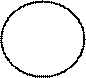
 3. Разностью двух множеств А и В
3. Разностью двух множеств А и В
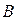

 называется С = А \ В,
называется С = А \ В,
каждый элемент 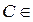 множеству А,
множеству А,
но  .
.
Пример: 

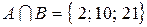
А \ В 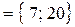
А \ В 
Понятие функции
Понятие функции является центральным для всей математики.
Опр.: Постоянной величиной называется величина сохраняющая одно и то же значение (π = 3,14…, е = 2,7182…).
Если величина сохраняет постоянное значение лишь в условиях данного процесса, то она называется параметром.
Опр.: Переменной называется величина, которая может принимать различные числовые значения.
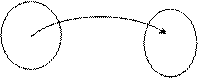
 Опр.: Если каждому элементу множества X
Опр.: Если каждому элементу множества X 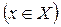 ставится в соответствие единственный элемент y множества Y
ставится в соответствие единственный элемент y множества Y  , то говорят, что на множестве X задана, функция
, то говорят, что на множестве X задана, функция 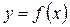 .
.
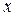

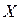

 X – область определения
X – область определения
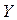 Y – область значения.
Y – область значения.
x – называется независимой переменной (аргументом)
y – зависимая переменная
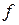 – обозначает знак соответствия
– обозначает знак соответствия
Опр.: Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий (+, –,:, *) n операций сложной функции, называется элементарными.
Опр.: Пусть функция  определена на множестве U с областью значений Y, а переменная U является функцией
определена на множестве U с областью значений Y, а переменная U является функцией 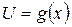 , определенной на множестве X с областью значений U. Тогда заданная на множестве функция
, определенной на множестве X с областью значений U. Тогда заданная на множестве функция 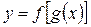 называется сложной функцией или композицией функций
называется сложной функцией или композицией функций 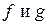 .
.
Обратная функция
Опр.: Пусть  :
: 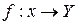 . Поставим в соответствие каждому
. Поставим в соответствие каждому  единственное значение
единственное значение 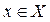 , при котором
, при котором 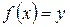 , тогда функция
, тогда функция 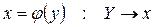 называется обратной.
называется обратной.
Вопросы:
1. Уравнение прямой и взаимное расположение прямых на плоскости.
2. Уравнение плоскости.
Уравнение плоскости
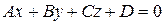 (1)
(1)
если 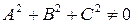 . Здесь А, В, С – координаты вектора
. Здесь А, В, С – координаты вектора 
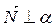 (вектор перпендикулярен плоскости)
(вектор перпендикулярен плоскости)
Частные случаи расположения плоскости:
а) 
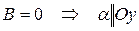
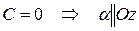
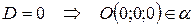
б) 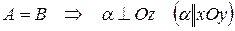

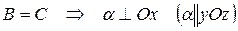
в) 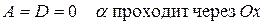
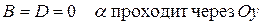
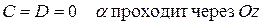
г) 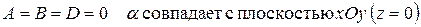
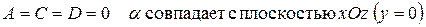
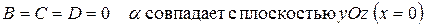
Уравнение плоскости в отрезках
Если в уравнении (1) 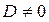 , то разделив уравнение на
, то разделив уравнение на 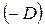 , получим:
, получим:
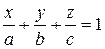 (2)
(2)

а, b, c – соответственно абсцисса, ордината и аппликата точек пересечения плоскости с осями Оx, Oy, Oz.
Уравнение плоскости, проходящей через 3 заданные точки 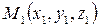 ;
; 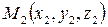 ;
; 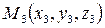 имеет вид:
имеет вид:
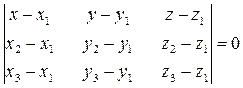 (3)
(3)
Прямые в пространстве
Прямая может быть задана уравнением двух плоскостей:
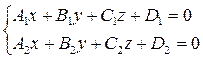 (8)
(8)
Уравнение прямой, проходящей через две точки 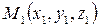 и
и 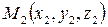
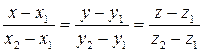 (9)
(9)
Каноническое уравнение прямой
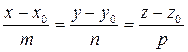 (10)
(10)
проходящей через точку 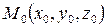 и параллельную вектору (направляющий вектор)
и параллельную вектору (направляющий вектор)
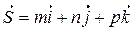 , т.е.
, т.е. 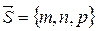
Параметрические уравнения прямой: приравняв (10) к t получим:
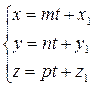 (11)
(11)
Вопросы:
1. Взаимное расположение прямой и плоскости в пространстве.
2. Кривые второго порядка.
2.1. Окружность.
2.2. Эллипс.
2.3. Гипербола.
2.4. Парабола.
Кривые второго порядка
Окружность
Опр.: Окружностью называют геометрическое место точек, одинаково удаленных от заданной точки, называемой центром.
Обозначим центр точкой если 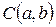 , а расстояние, на которое точки окружности удалены от центра называются радиусом: (R).
, а расстояние, на которое точки окружности удалены от центра называются радиусом: (R).
Выведем каноническое уравнение окружности:
Возьмем на окружности текущую точку 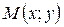 , по формуле расстояния между двумя заданными точками:
, по формуле расстояния между двумя заданными точками:
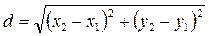
Получим: 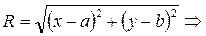
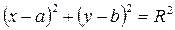 (1)
(1)
Если центр окружности находится в начале координат, то уравнение (1) упрощается: 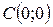
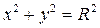 (1')
(1')
Эллипс
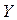 Опр.: Эллипс – геометрическое место точек сумма расстояний от которых до двух заданных точек (называемых фокусами) – есть величина постоянная (равная 2 а).
Опр.: Эллипс – геометрическое место точек сумма расстояний от которых до двух заданных точек (называемых фокусами) – есть величина постоянная (равная 2 а).
Расстояние между фокусами F 1 и F 2 равно 2 с
а > c
r 1 и r 2 – фокальные радиусы
Выведем каноническое уравнение эллипса для случая, когда его фокусы лежат на оси Ox, симметрично относительно начала координат.
Возьмем на эллипсе текущую точку 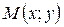 . По определения эллипса
. По определения эллипса
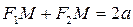
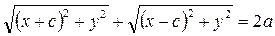
После элементарных преобразований (сделать самостоятельно), получим уравнение:
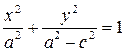
Обозначим 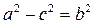 , получим:
, получим:
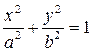 (2)
(2)
– каноническое уравнение эллипса.
Точки 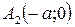 ,
, 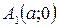 и
и 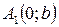 ,
, 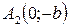 – вершины эллипса.
– вершины эллипса.
А 1 А 2 – большая ось = 2 а
В 1 В 2 – малая ось = 2 b
а – большая полуось
b – малая полуось
Показатель «выпуклости» эллипса – эксцентриситет:
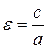
т.к. 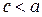 , то
, то 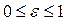
если 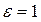 – окружность.
– окружность.
Гипербола
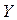

 Опр.: Гиперболой называют геометрическое место точек на плоскости, абсолютная величина разности расстояний от которых до двух заданных точек (называются фокусами) величина постоянная и равна 2 а, причем 2 а < 2 с ⇒ а < с.
Опр.: Гиперболой называют геометрическое место точек на плоскости, абсолютная величина разности расстояний от которых до двух заданных точек (называются фокусами) величина постоянная и равна 2 а, причем 2 а < 2 с ⇒ а < с.
Каноническое уравнение гиперболы аналогично эллипсу:
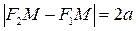
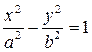 (3)
(3)
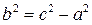
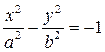 – сопряженная гипербола
– сопряженная гипербола
Гипербола строится из а и b.
Перепишем уравнение гиперболы в виде:
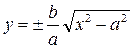
при 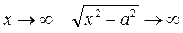 и уравнение принимает вид:
и уравнение принимает вид: 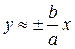
т.е. при 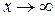 ветви гиперболы как угодно близко подходят к прямым
ветви гиперболы как угодно близко подходят к прямым
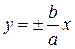 – асимптоты гиперболы.
– асимптоты гиперболы.
Оx – действительная ось гиперболы
Оy – линейная ось гиперболы
эксцентриситет 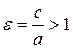 , т.к. с > 0
, т.к. с > 0
Оптические свойства:
1. Лучи света, выходящие из 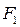 эллипса после отображения от эллипса проходят через
эллипса после отображения от эллипса проходят через 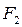 .
.
2. Лучи, исходящие из одного фокуса гиперболы после зеркального отображения – мнимый фокус 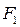 .
.
3. Лучи света из 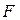 параболы после отражения образуют пучок параллельный оси параболы.
параболы после отражения образуют пучок параллельный оси параболы.
Парабола
Опр.: Параболой называется геометрическое месторасположение точек на плоскости равноудаленных от заданной точки-фокуса и заданной прямой, называемой директрисой.
Расстояние от фокуса до директрисы равно p.
Выведем каноническое уравнение параболы для случая, когда, его фокус лежит на оси Ох. ⇒ Директриса перпендикулярна оси Ох, а начало координат делит расстояние от фокуса до директрисы пополам.
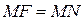
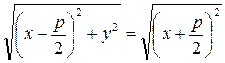
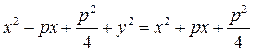
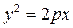 (5)
(5)
– каноническое уравнение параболы.
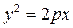 – ветви вправо, если p > 0
– ветви вправо, если p > 0
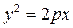 – ветви влево, если p < 0
– ветви влево, если p < 0
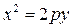 – ветви вверх, если p > 0
– ветви вверх, если p > 0
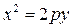 – ветви вниз, если p < 0
– ветви вниз, если p < 0
Вершина параболы может находиться в точке 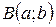 , тогда:
, тогда:
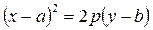
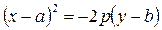
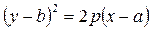
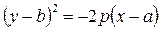
Лекция 2. ТЕОРИЯ ПРЕДЕЛОВ.
1. Предел числовой последовательности.
2. Предел функции в бесконечности и в точке.
3. Замечательные пределы.
4. Непрерывность функции Основные теоремы о пределах
Основные теоремы о пределах
Бесконечно большая величина – переменная, предел которой равен + ∞ или
– ∞.
Бесконечно малая величина – переменная, предел которой равен 0.
Свойства:
1. 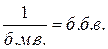 и
и 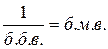
2. Если а и b – б.м.в., то
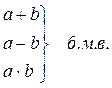
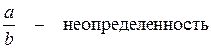
3. Если а и b – б.б.в., то
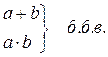
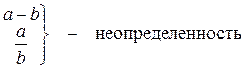
Теорема 1: Предел постоянной равен самой этой постоянной, т.к. если
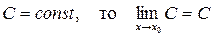
Теорема 2: Пусть существует 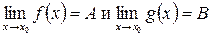 , тогда
, тогда
1) 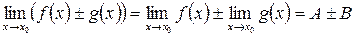
2) 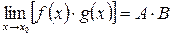
3) Если В ≠ 0, то 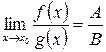
Лемма («о двух милиционерах»)
Если функции 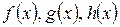 удовлетворяют условию
удовлетворяют условию 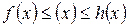 и если
и если 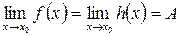 , то
, то 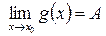 .
.
Примеры: вычисления пределов и раскрытие неопределенностей
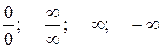
1. 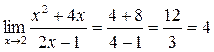
2. 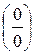
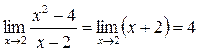
3. 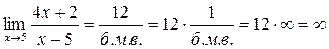
4. 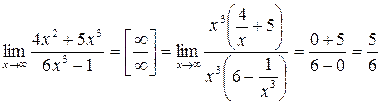
5. 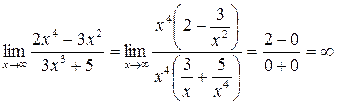
6. 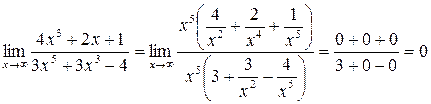
7. 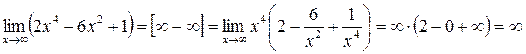
Замечательные пределы
Первый замечательный предел 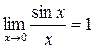
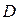
 Доказательство:
Доказательство:
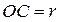
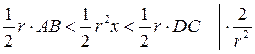
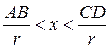
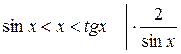
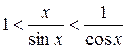
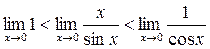
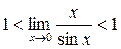
по лемме о двух милиционерах:
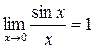
Второй замечательный предел 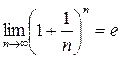
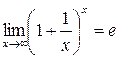
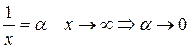
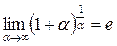
Функция 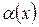 называется бесконечно малой функцией при
называется бесконечно малой функцией при 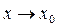 , если
, если
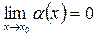
Если 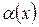 и
и 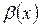 – б.м.ф., то
– б.м.ф., то
1) 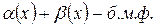
2) 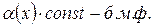
3) произведение б.м.ф. на ограниченную функцию есть б.м.ф.
Бесконечно большая функция 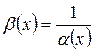
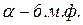
Опр.: Две функции 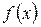 и
и 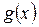 называются эквивалентными при
называются эквивалентными при 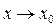 , если
, если 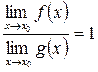 обозначается
обозначается 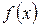 ∼
∼ 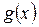
Пример:
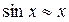
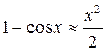
при 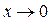
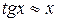
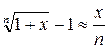
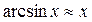
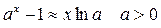
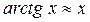
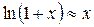
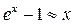
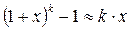
Непрерывность функции
Опр.: Функция 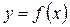 называется непрерывной в точке х 0, если она определена в некоторой окрестности этой точки и
называется непрерывной в точке х 0, если она определена в некоторой окрестности этой точки и 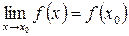
Функция называется непрерывной слева (справа) в точке 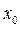 , если она определена в некоторой окрестности слева (справа) от точки
, если она определена в некоторой окрестности слева (справа) от точки 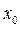 и
и
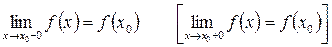
Опр.: Функция называется непрерывной в интервале, если она непрерывна в каждой точке этого интервала.
Опр.: Точки, в которых, функция не является непрерывной называются точками разрыва.
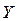
 Классификация точек разрыва
Классификация точек разрыва
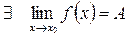
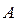


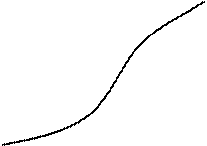 1.
1.
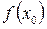

 Если
Если
т.е.
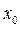
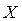
 но
но
(если в точке 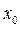 функция не определена)
функция не определена)
то 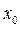 – точка устранимого разрыва I-го разряда.
– точка устранимого разрыва I-го разряда.
Пример:
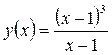 при
при 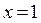 функция неопределенна.
функция неопределенна.
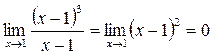
т.о. 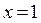 – точка устраняемого разрыва 1-го рода.
– точка устраняемого разрыва 1-го рода.
Доопределив функцию в токе 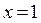 , получим:
, получим:
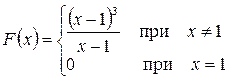
Новая функция будет уже непрерывна в точке 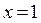 .
.
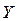
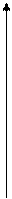 2.
2.
то 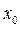 – точка конечного разрыва I-го рода.
– точка конечного разрыва I-го рода. 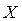
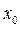

Опр.: Скачком функции в точке разрыва I-го рода называется величина:
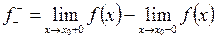
Пример:
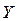

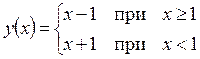
 при
при 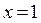
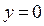


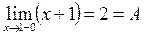
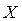
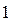

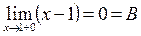
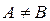 в точке
в точке 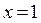 разрыв I рода.
разрыв I рода.
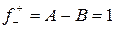
3. Все остальные – точки разрыва II рода.
Пример:
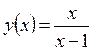 при
при 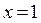 функция неопределенна
функция неопределенна
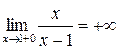
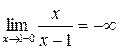
Т.к. односторонние пределы (достаточно было бы одного) бесконечны, то 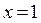 – точка разрыва II-го рода.
– точка разрыва II-го рода.
Примеры вычисления замечательных приделов:
1. 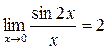 т.к.
т.к. 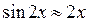
2. 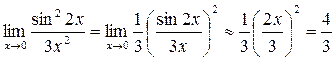
3. 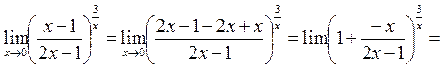
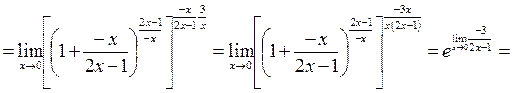
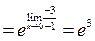
т.к. 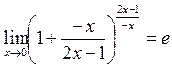 при
при 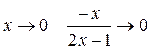
Правила дифференцирования
Схема вычисления производной:
1. Дать аргументу приращение 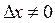 , найти значения функции
, найти значения функции 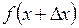 .
.
2. Найти приращение функции 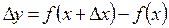 .
.
3. Составить отношение 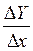
4. Найдем предел этого отношения при 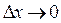 , т.е.
, т.е. 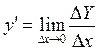 (если этот придел существует).
(если этот придел существует).
Пример: 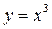
1. 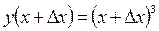
2. 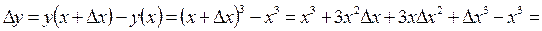
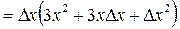
3. 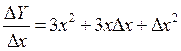
4. 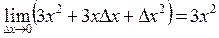
Т.о. 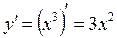 .
.
Можно доказать, что 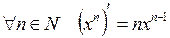 .
.
Правила дифференцирования:
1. 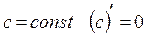
2. 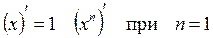
3. 
4. 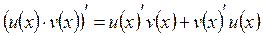
5. 
6. 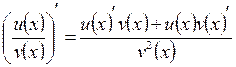
Таблица производных:
1. 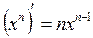
2. 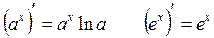
3. 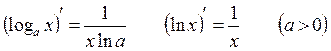
4. 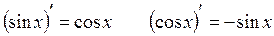
5. 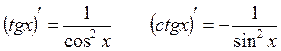
6. 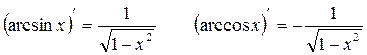
7. 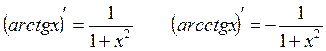
Производная сложной функции:
Теорема: Если 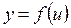 и
и 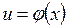 – дифференцируемы функции от своих аргументов, то производная сложной функции:
– дифференцируемы функции от своих аргументов, то производная сложной функции:
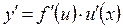
Действительно:
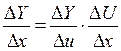
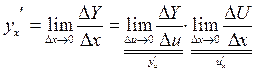
Пример:
1) 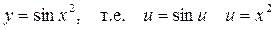
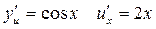 , получим
, получим 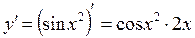
2) 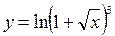

Производная обратной функции:
Дифференцируемая функция 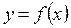 с производной
с производной 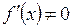 имеет однозначную непрерывную обратную функцию
имеет однозначную непрерывную обратную функцию  , причем обратная функция так же дифференцируема и справедлива формула:
, причем обратная функция так же дифференцируема и справедлива формула:

Пример:

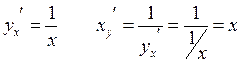
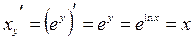
Первообразная функции
Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции.
Интегральное счисление решает обратную задачу – нахождение самой функции по ее производной или дифференциалу.
Опр.: Функция  называется первообразной функцией для функции
называется первообразной функцией для функции  на промежутке Х, если в каждой точке х этого промежутка
на промежутке Х, если в каждой точке х этого промежутка

Например:
1)  является первообразной для функции
является первообразной для функции  , т.к.
, т.к.

2.  на промежутке
на промежутке  для
для  , т.е.
, т.е.
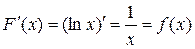
Исходя из геометрического смысла производной:  – угловой коэффициент касательной к кривой
– угловой коэффициент касательной к кривой  в точке х
в точке х
 Значит, найти первообразную для
Значит, найти первообразную для  – найти такую кривую
– найти такую кривую  , что угловой коэффициент касательной к ней в произвольной точке х равен значению
, что угловой коэффициент касательной к ней в произвольной точке х равен значению  заданной функции в этой точке
заданной функции в этой точке
Следует заметить, что для заданной функции  ее первообразная определена неоднозначно.
ее первообразная определена неоднозначно.
Например:
Функции  ,
,  и вообще функции
и вообще функции  , где С – некоторое действительное число, являются первообразными для функции
, где С – некоторое действительное число, являются первообразными для функции

В общем случае, если  – некоторая первообразная для
– некоторая первообразная для  , то поскольку
, то поскольку

функции вида  , где С – произвольное число так же являются первообразными для
, где С – произвольное число так же являются первообразными для  .
.
Геометрически это означает, что если найдена одна кривая  , удовлетворяющая условию
, удовлетворяющая условию  , то сдвигая ее вдоль оси Оу, мы вновь получаем кривые, удовлетворяющие указанному условию (поскольку такой сдвиг не меняет углового коэффициента касательной).
, то сдвигая ее вдоль оси Оу, мы вновь получаем кривые, удовлетворяющие указанному условию (поскольку такой сдвиг не меняет углового коэффициента касательной).
Опр.: Совокупность всех первообразных для функции  на промежутке Х называется неопределенным интегралом от функции
на промежутке Х называется неопределенным интегралом от функции  .
.
Обозначение: 
 – знак интеграла
– знак интеграла
х – переменная интегрирования
 – подинтегральная функция
– подинтегральная функция
 – подинтегральное выражение
– подинтегральное выражение
Пример:
1) 
2) 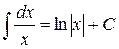
Операция нахождения неопределенного интеграла от некоторой функции называется интегрирование функции (обратная к операции дифференцирования).
Таблица интегралов основных элементарных функций
1. 
2. 
3. 
4. 
5. 
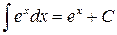
6. 
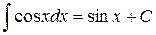
7. 

8. 

9. 
10. 
11. 

Справедливость приведенных формул проверяется дифференцированием:
Пример:

Примеры:
1. 
2. 
3. 
4. 
5. 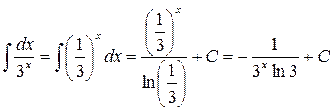
6. 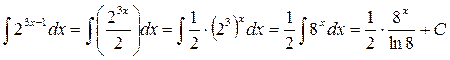
7. 


Метод замены переменной
Пусть 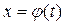 – функция, дифференцируемая на промежутке X, тогда
– функция, дифференцируемая на промежутке X, тогда
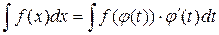
Доказательство:
Продифференцируем обе части этого равенства попеременной t:
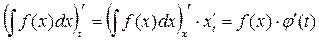
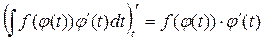
так как принимает 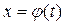 , то равенство верно.
, то равенство верно.
Пример:
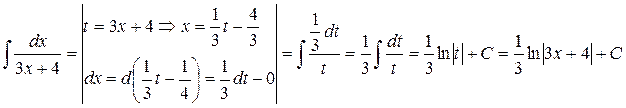
Замечание:
Новую переменную можно не выписывать явно, а интегрировать путем внесения множителя под знак дифференциала.
Исходя из свойств дифференциала:
а) Постоянный множитель
1) 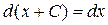
2) 
|
|
|



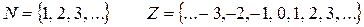

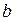
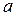
 Если
Если 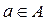


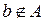
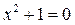

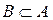
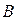
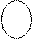 B является подмножеством А,
B является подмножеством А,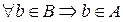
 .
.

 1. Объединение
1. Объединение 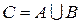
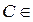 хотя бы
хотя бы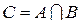 каждый элемент
каждый элемент 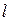 принадлежащий и множеству А, и множеству В.
принадлежащий и множеству А, и множеству В.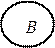

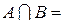 Ø
Ø
 3. Разностью двух множеств А и В
3. Разностью двух множеств А и В называется С = А \ В,
называется С = А \ В, .
.

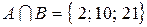
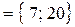

 Опр.: Если каждому элементу множества X
Опр.: Если каждому элементу множества X 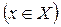 ставится в соответствие единственный элемент y множества Y
ставится в соответствие единственный элемент y множества Y  , то говорят, что на множестве X задана, функция
, то говорят, что на множестве X задана, функция 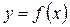 .
.
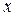

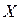

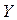 Y – область значения.
Y – область значения.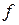 – обозначает знак соответствия
– обозначает знак соответствия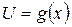 , определенной на множестве X с областью значений U. Тогда заданная на множестве функция
, определенной на множестве X с областью значений U. Тогда заданная на множестве функция 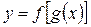 называется сложной функцией или композицией функций
называется сложной функцией или композицией функций 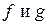 .
.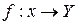 . Поставим в соответствие каждому
. Поставим в соответствие каждому  единственное значение
единственное значение 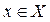 , при котором
, при котором 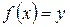 , тогда функция
, тогда функция 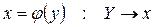 называется обратной.
называется обратной.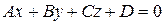 (1)
(1)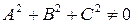 . Здесь А, В, С – координаты вектора
. Здесь А, В, С – координаты вектора 
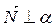 (вектор перпендикулярен плоскости)
(вектор перпендикулярен плоскости)
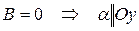
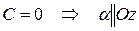
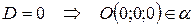
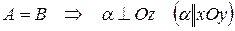

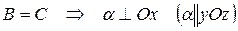
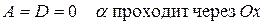
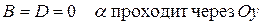
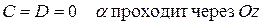
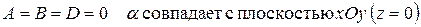
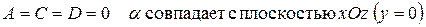
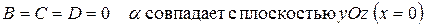
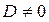 , то разделив уравнение на
, то разделив уравнение на 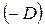 , получим:
, получим: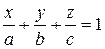 (2)
(2)
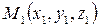 ;
; 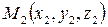 ;
; 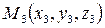 имеет вид:
имеет вид: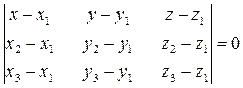 (3)
(3)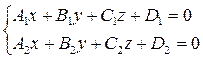 (8)
(8)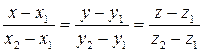 (9)
(9)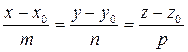 (10)
(10)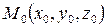 и параллельную вектору (направляющий вектор)
и параллельную вектору (направляющий вектор)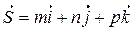 , т.е.
, т.е. 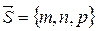
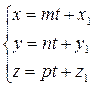 (11)
(11)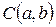 , а расстояние, на которое точки окружности удалены от центра называются радиусом: (R).
, а расстояние, на которое точки окружности удалены от центра называются радиусом: (R).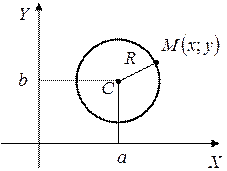
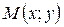 , по формуле расстояния между двумя заданными точками:
, по формуле расстояния между двумя заданными точками: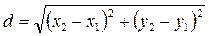
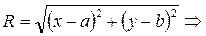
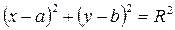 (1)
(1)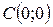
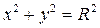 (1')
(1')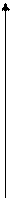
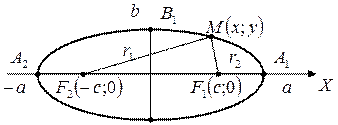
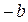
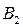
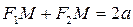
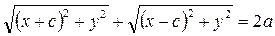
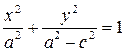
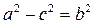 , получим:
, получим: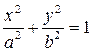 (2)
(2)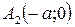 ,
, 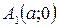 и
и 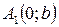 ,
, 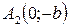 – вершины эллипса.
– вершины эллипса.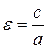
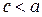 , то
, то 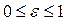
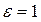 – окружность.
– окружность.
 Опр.: Гиперболой называют геометрическое место точек на плоскости, абсолютная величина разности расстояний от которых до двух заданных точек (называются фокусами) величина постоянная и равна 2 а, причем 2 а < 2 с ⇒ а < с.
Опр.: Гиперболой называют геометрическое место точек на плоскости, абсолютная величина разности расстояний от которых до двух заданных точек (называются фокусами) величина постоянная и равна 2 а, причем 2 а < 2 с ⇒ а < с.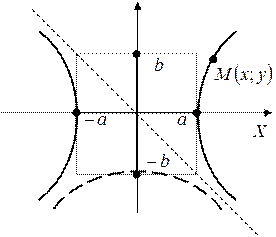
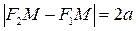
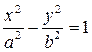 (3)
(3)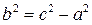
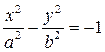 – сопряженная гипербола
– сопряженная гипербола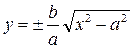
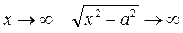 и уравнение принимает вид:
и уравнение принимает вид: 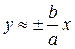
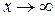 ветви гиперболы как угодно близко подходят к прямым
ветви гиперболы как угодно близко подходят к прямым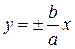 – асимптоты гиперболы.
– асимптоты гиперболы.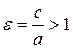 , т.к. с > 0
, т.к. с > 0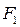 эллипса после отображения от эллипса проходят через
эллипса после отображения от эллипса проходят через 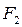 .
.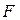 параболы после отражения образуют пучок параллельный оси параболы.
параболы после отражения образуют пучок параллельный оси параболы.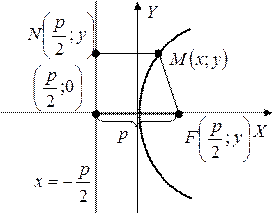
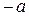
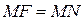
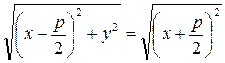
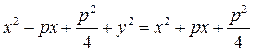
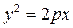 (5)
(5)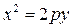 – ветви вверх, если p > 0
– ветви вверх, если p > 0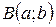 , тогда:
, тогда: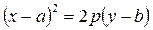
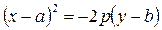
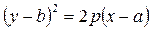
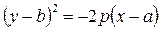
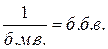 и
и 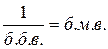
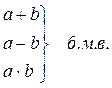
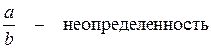
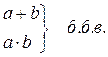
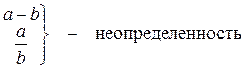
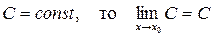
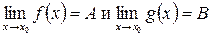 , тогда
, тогда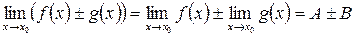
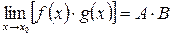
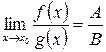
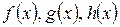 удовлетворяют условию
удовлетворяют условию 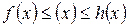 и если
и если 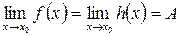 , то
, то 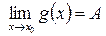 .
.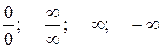
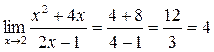
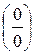
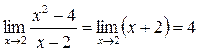
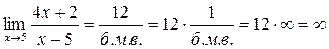
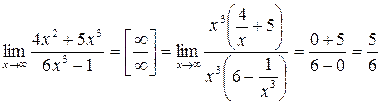
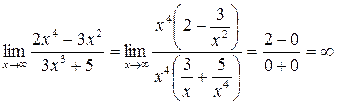
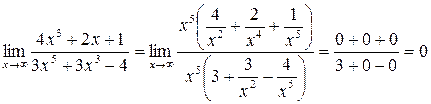
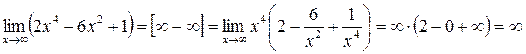
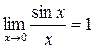
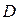
 Доказательство:
Доказательство: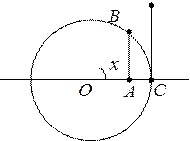
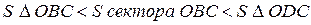
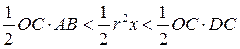
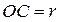
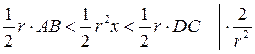
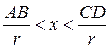
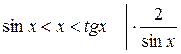
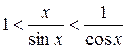
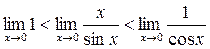
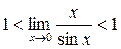
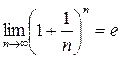
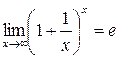
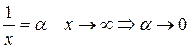
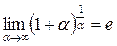
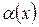 называется бесконечно малой функцией при
называется бесконечно малой функцией при 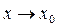 , если
, если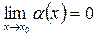
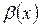 – б.м.ф., то
– б.м.ф., то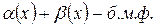
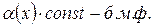
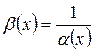
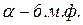
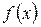 и
и 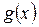 называются эквивалентными при
называются эквивалентными при 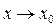 , если
, если 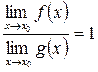 обозначается
обозначается 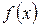 ∼
∼ 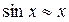
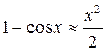
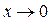
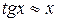
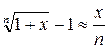
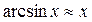
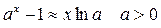
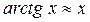
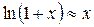
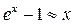
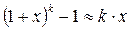
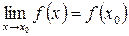

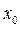 , если она определена в некоторой окрестности слева (справа) от точки
, если она определена в некоторой окрестности слева (справа) от точки 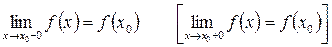
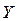
 Классификация точек разрыва
Классификация точек разрыва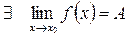
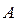

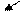

 1.
1.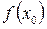

 Если
Если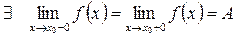
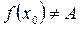
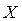
 но
но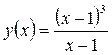 при
при 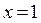 функция неопределенна.
функция неопределенна.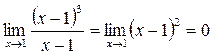
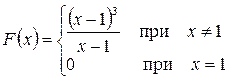
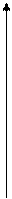 2.
2.
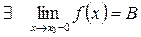
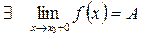
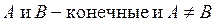
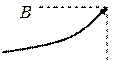

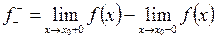

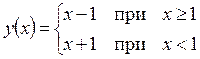
 при
при 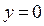


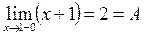

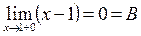
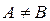 в точке
в точке 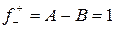
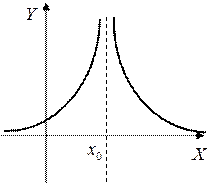
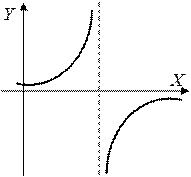
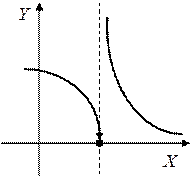
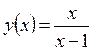 при
при 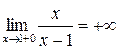
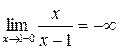
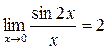 т.к.
т.к. 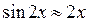
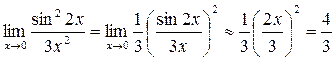
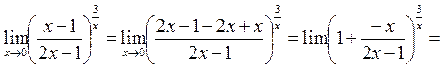
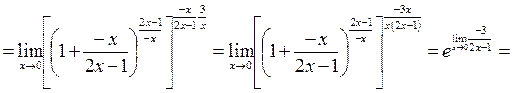
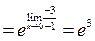
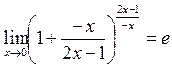 при
при 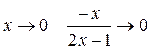
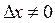 , найти значения функции
, найти значения функции 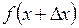 .
.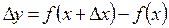 .
.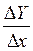
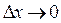 , т.е.
, т.е. 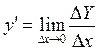 (если этот придел существует).
(если этот придел существует).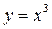
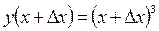
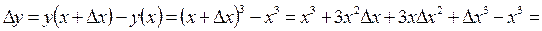
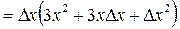
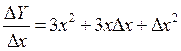
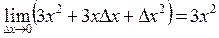
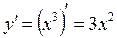 .
.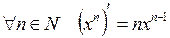 .
.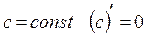
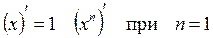

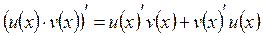

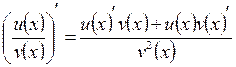
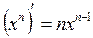
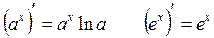
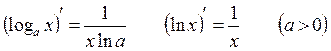
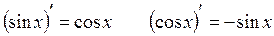
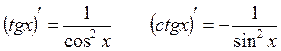
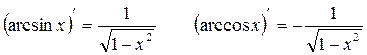
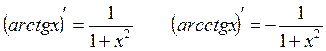
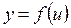 и
и 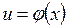 – дифференцируемы функции от своих аргументов, то производная сложной функции:
– дифференцируемы функции от своих аргументов, то производная сложной функции: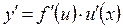
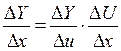
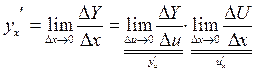
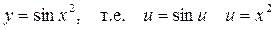
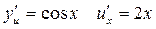 , получим
, получим 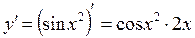
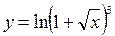

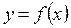 с производной
с производной 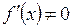 имеет однозначную непрерывную обратную функцию
имеет однозначную непрерывную обратную функцию  , причем обратная функция так же дифференцируема и справедлива формула:
, причем обратная функция так же дифференцируема и справедлива формула:

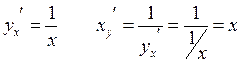
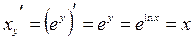
 называется первообразной функцией для функции
называется первообразной функцией для функции  на промежутке Х, если в каждой точке х этого промежутка
на промежутке Х, если в каждой точке х этого промежутка
 является первообразной для функции
является первообразной для функции  , т.к.
, т.к.
 на промежутке
на промежутке  для
для  , т.е.
, т.е.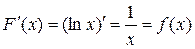
 – угловой коэффициент касательной к кривой
– угловой коэффициент касательной к кривой  в точке х
в точке х Значит, найти первообразную для
Значит, найти первообразную для 
 ,
,  и вообще функции
и вообще функции  , где С – некоторое действительное число, являются первообразными для функции
, где С – некоторое действительное число, являются первообразными для функции

 , где С – произвольное число так же являются первообразными для
, где С – произвольное число так же являются первообразными для  , то сдвигая ее вдоль оси Оу, мы вновь получаем кривые, удовлетворяющие указанному условию (поскольку такой сдвиг не меняет углового коэффициента касательной).
, то сдвигая ее вдоль оси Оу, мы вновь получаем кривые, удовлетворяющие указанному условию (поскольку такой сдвиг не меняет углового коэффициента касательной).
 – знак интеграла
– знак интеграла – подинтегральное выражение
– подинтегральное выражение
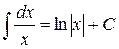





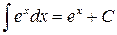

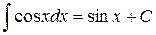













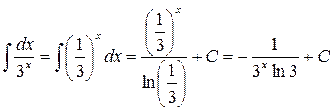
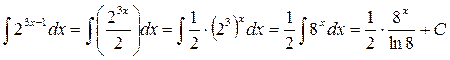



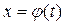 – функция, дифференцируемая на промежутке X, тогда
– функция, дифференцируемая на промежутке X, тогда