Отметим еще раз, что в «Началах» свойство единственности разложения на простые делители не сформулировано, но от этого сама арифметика «Начал» ничего не потеряла: то, что можно вывести из основной теоремы арифметики, получено там на основе теоремы Евклида. Легко могло бы быть получено и само свойство единственности. Сейчас мы это сделаем.
Пусть имеем два разложения на простые делители
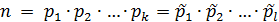 . (1)
. (1)
Докажем, что число множителей в обоих разложениях одинаково и после подходящей перестановки множителей 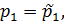
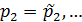 Можно предполагать, что
Можно предполагать, что 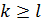 . Если
. Если 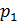 делится на
делится на 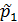 , то из определения простого числа вытекает, что они равны. Если
, то из определения простого числа вытекает, что они равны. Если 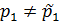 , то по теореме Евклида произведение
, то по теореме Евклида произведение 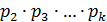 делится на
делится на 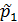 . Продолжая и далее эти рассуждения, получим, что
. Продолжая и далее эти рассуждения, получим, что 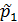 совпадает с одним из
совпадает с одним из 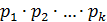 . Перестановкой множителей можно добиться того, что
. Перестановкой множителей можно добиться того, что 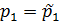 . После сокращения (1) на
. После сокращения (1) на 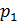 , имеем равенство
, имеем равенство 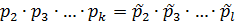 и, повторяя предыдущий шаг, получим
и, повторяя предыдущий шаг, получим 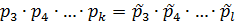 . После
. После 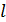 таких шагов справа останется 1, а слева
таких шагов справа останется 1, а слева 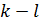 простых множителей. Поэтому
простых множителей. Поэтому 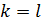 и однозначность установлена.
и однозначность установлена.
Кроме теоремы Евклида мы использовали только определение простого числа и закон сокращения: если 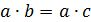 и
и 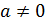 , то
, то 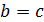 .
.
Чтобы окончательно доказать теорему Евклида, необходимо обосновать соотношение Безу, а для этого требуется предварительно развить теорию наибольшего общего делителя двух целых чисел. Именно для этой цели будут востребованы самые существенные свойства целых чисел.
От натуральных чисел перейдем к множеству целых чисел Z =
= {0, ±1, ±2,...} и наряду с натуральным простым р число –р также назовем простым. Разложению на простые подлежат все числа, отличные от 0 и ±1, например 6 = 2∙3 = 3∙2 = (–2)∙(–3) = (–3)∙(–2). Видим, что разложение единственно с точностью до перестановки множителей и их знаков.
Формулировка основной теоремы арифметики для целых чисел меняется незначительно: любое число, отличное от нуля и от ±1, можно разложить на простые множители, причем это разложение единственно с точностью до порядка множителей и их знаков.
Сначала рассмотрим алгори́тм Евкли́да – алгоритм для нахождения наибольшего общего делителя двух целых чисел или наибольшей общей меры двух однородных величин.
История
Древнегреческие математики называли этот алгоритм ἀνθυφαίρεσις или ἀνταναίρεσις – «взаимное вычитание». Этот алгоритм не был открыт Евклидом, так как упоминание о нём имеется уже в Топике Аристотеля. В «Началах» Евклида он описан дважды – в VII книге для нахождения наибольшего общего делителя двух натуральных чисел и в X книге для нахождения наибольшей общей меры двух однородных величин. В обоих случаях дано геометрическое описание алгоритма, для нахождения «общей меры» двух отрезков.
Историками математики (Цейтен и др.) было выдвинуто предположение, что именно с помощью алгоритма Евклида (процедуры последовательного взаимного вычитания) в древнегреческой математике впервые было открыто существование несоизмеримых величин (стороны и диагонали квадрата, или стороны и диагонали правильного пятиугольника). Впрочем, это предположение не имеет достаточных документальных подтверждений. Алгоритм для поиска наибольшего общего делителя двух натуральных чисел описан также в I книге древнекитайского трактата Математика в девяти книгах.
Ряд математиков средневекового Востока (Сабит ибн Курра, ал-Махани, Ибн ал-Хайсам, Омар Хайям) попытались построить на основе алгоритма Евклида теорию отношений, альтернативную по отношению теории отношений Евдокса, изложенной в V книге «Начал» Евклида. Согласно определению, предложенному этими авторами, четыре величины, первая ко второй и третья к четвёртой, имеют между собой одно и то же отношение, если при последовательном взаимном вычитании второй величины в обеих парах на каждом шаге будут получаться одни и те же неполные частные.





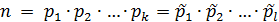 . (1)
. (1)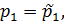
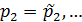 Можно предполагать, что
Можно предполагать, что 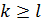 . Если
. Если 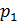 делится на
делится на 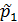 , то из определения простого числа вытекает, что они равны. Если
, то из определения простого числа вытекает, что они равны. Если 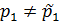 , то по теореме Евклида произведение
, то по теореме Евклида произведение 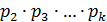 делится на
делится на 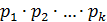 . Перестановкой множителей можно добиться того, что
. Перестановкой множителей можно добиться того, что 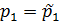 . После сокращения (1) на
. После сокращения (1) на 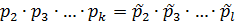 и, повторяя предыдущий шаг, получим
и, повторяя предыдущий шаг, получим 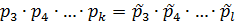 . После
. После 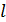 таких шагов справа останется 1, а слева
таких шагов справа останется 1, а слева 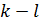 простых множителей. Поэтому
простых множителей. Поэтому 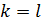 и однозначность установлена.
и однозначность установлена.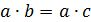 и
и 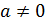 , то
, то 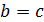 .
.


