Тематические обзоры по курсу элементарной математики
Составитель В.Г.Ермаков
Тема I. Числовые системы
1. Натуральные числа [1]
Ряд натуральных чисел
Еще в глубокой древности потребности обмена, торговли, скотоводства и т. п. привели людей к необходимости уметь считать предметы.
Числа, которые используют при подсчете предметов, называют натуральными числами.
Таким образом, числа: один, два, три,..., десять,..., сто,..., тысяча,..., миллион,..., миллиард,... – натуральные числа.
Натуральные числа
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,...,
записанные в порядке возрастания и без пропусков, образуют натуральный ряд, или ряд натуральных чисел.
На первом месте в натуральном ряду стоит число 1, за ним следует число 2, затем число 3 и так далее.
В натуральном ряду есть первое число 1, но нет последнего числа – за каждым натуральным числом следует еще одно натуральное число, большее предшествующего на единицу. Поэтому все натуральные числа записать невозможно, и при записи натурального ряда выписывают подряд несколько первых чисел, после которых ставят многоточие (три точки).
Отсутствие предметов для счета условились обозначать числом нуль.
Нуль не считают натуральным числом.
Десятичная система записи натуральных чисел
Практическая деятельность потребовала от человека умения не только считать, но и умения записывать числа. В старину для записи натуральных чисел использовались и особые рисунки, и черточки, и буквы, и т. п. В настоящее время принята десятичная система записи чисел (десятичная система счисления), в которой числа записывают при помощи десяти знаков:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Эти знаки называют цифрами.
При этом одна и та же цифра имеет различное значение в зависимости от того места (позиции), где она расположена в записи числа. Например, в записи числа 777 первая справа цифра 7 означает семь единиц, вторая – семь десятков, третья – семь сотен.
Поэтому десятичную систему счисления называют позиционной.
Сравнение натуральных чисел
Числа можно сравнивать при помощи натурального ряда.
Из двух натуральных чисел больше то, которое в ряду натуральных чисел стоит правее (дальше от начала).
Если a, b, c – натуральные числа и число b в ряду натуральных чисел находится правее числа а, а число с находится правее числа b, то из этого следует, что число с находится правее числа а, то есть из а < b и b < с следует, что а < с.
В таких случаях пишут: а < b < с и говорят: «b больше а, но меньше с». Если числа а и b равны, то пишут а = b.
Каждое натуральное число а больше нуля; это записывают так:
а > 0.
Число, большее нуля, называют положительным.
Поэтому натуральные числа называют еще целыми положительными числами. Число нуль также целое, но не положительное число.
Натуральные числа и число нуль называют еще целыми неотрицательными числами, так как кроме неотрицательных чисел есть еще и отрицательные числа. О них будет сказано ниже.
Если к ряду натуральных чисел приписать слева число 0, то получится ряд неотрицательных целых чисел:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,....
Сложение. Законы сложения
Чтобы сложить числа 5 и 3, можно рассуждать так. Рассмотрим ряд натуральных чисел, отметим в этом ряду число 5 и отсчитаем от него вправо 3 числа. Получится число 8, называемое суммой чисел 5 и 3:
8 = 5 + 3.
Числа 5 и 3 называют слагаемыми.
Но можно отметить в натуральном ряду сначала число 3 и отсчитать от него вправо 5 чисел. Получится то же число 8, называемое суммой чисел 3 и 5:
8=3 + 5.

Для любых натуральных чисел а и b верно равенство: a + b = b + a, выражающее переместительный закон сложения:
От перестановки слагаемых сумма не меняется.
Для любых натуральных чисел a, b и с верно равенство:
(a + b) + c = a + (b + c), выражающее сочетательный закон сложения:
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.
Переместительный и сочетательный законы сложения верны для любых неотрицательных чисел. Например, 5 + 0 = 0 + 5; (5 + 3)+0 = 5 +(3 + 0).
В сумме нескольких слагаемых можно менять слагаемые местами и заключать их в скобки любым образом.
Вычитание
Разностью чисел а и b называют такое число, которое при сложении с числом b дает число а. Число а называют уменьшаемым, число b – вычитаемым.
Разность чисел а и b обозначают а – b.
Таким образом, (a – b) + b = a или a – b + b = a.
Покажем, как, используя натуральный ряд чисел, можно найти разность натуральных чисел а и b в случае, когда а > b.
Пусть надо найти разность 9 – 6. Отметим в натуральном ряду число 9 и отсчитаем от него влево шесть чисел. Получим число 3. Легко видеть, что сумма чисел 3 и 6 равна 9:
3 + 6 = 9.
Поэтому число 3 есть разность чисел 9 и 6, т. е. 9 – 6 = 3.
Замечание. С помощью неотрицательных целых чисел можно вычислить разность а и b только в том случае, когда а больше или равно b (пишут: а ≥ b). В дальнейшем будут введены новые числа – отрицательные, с помощью которых можно будет из меньшего числа вычесть большее.
Умножение. Законы умножения
Умножить натуральное число 3 на натуральное число 4 – значит найти сумму трех слагаемых, каждое из которых 4. Получится число 12, называемое произведением чисел 3 и 4.
Таким образом,
3∙4 = 4 + 4 + 4 = 12.
Числа 3 и 4 называют множителями.
Для любого числа а верно равенство:
1∙а = а.
Примеры. 5∙3 = 3 + 3 + 3 + 3 + 3 = 15, 3∙5=5 + 5 + 5 = 15, 3∙1 = 1 + 1 + 1=3,
1∙7=7.
Для любых натуральных чисел а и b верно равенство: a∙b = b∙a, выражающее переместительный закон умножения:
От перестановки множителей произведение не меняется.

| 
|
| а)
| б)
|
| Рис. 1
|
Переместительный закон умножения легко проверить при подсчете двумя способами числа квадратов на рисунке 1. Все квадраты можно расположить в 3 ряда по 4 квадрата – всего 3∙4 квадрата (рис. 1, а). Но можно расположить все квадраты в 4 ряда по 3 квадрата – всего 4∙3 квадрата (рис. 1, б). Так как число квадратов в обоих случаях одно и то же, то
3∙4=4∙3.
Для любых натуральных чисел а, b и с верно равенство:
(а∙b)∙с = а∙(b∙с),
выражающее сочетательный закон умножения:
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.
Сочетательный закон умножения легко проверить путем подсчета числа кубиков, как это сделано на рисунке 2 в цитируемом учебнике.
Из законов умножения следует, что в произведении нескольких множителей можно менять местами множители и заключать их в скобки любым способом.
Отметим, что для любого натурального числа а верны равенства:
а∙0 = 0, 0∙а=0.
Кроме того, 0∙0 = 0.
Поэтому равенства а∙b=b∙а и (а∙b)∙с=а∙(b∙с) верны для любых целых неотрицательных чисел.
Например, 5∙0 = 0∙5, (5∙3)∙0 = 5∙(3∙0).
Деление нацело
Пусть а и b – натуральные числа и а больше или равно b (а ≥ b). Говорят, что а делится на b нацело, если существует натуральное число с, при умножении которого на b получается а:
a = b∙c.
Обычно слово «нацело» в этой фразе опускается. При этом пишут: а:b = с и называют а – делимым, b – делителем, с – частным.
Любое натуральное число а делится на 1 и само на себя:
a:l = a, а:а = 1, так как a∙l = a, 1∙а = а.
Например, 12 делится на 1 и на 12.
При делении нуля на любое натуральное число получается нуль:
0:а = 0, потому что 0∙а = 0.
Делить на нуль нельзя.
Делить на нуль нельзя, потому что для любого натурального числа а не существует такого числа с, для которого выполнялось бы равенство а:0 = с, так как с∙0 = 0.
При делении нуля на нуль можно было бы считать, что 0:0 = с, потому что с∙0 = 0. Но в этом случае частным могло бы быть любое число с. Поэтому считают, что и нуль на нуль делить нельзя.
Отметим важное свойство частного: делимое и делитель можно умножить или разделить нацело на одно и то же натуральное число – частное от этого не изменится.
Например, 48:24 = 2,
(48∙2):(24∙2) = 96:48 = 2; (48:2):(24:2) = 24:12 = 2.
Это верно и в общем случае. В самом деле, если а:b = с (и значит, а = c∙b), то c∙(k∙b) = (c∙k)∙b = (k∙c)∙b = k∙(c∙b) = k∙a. Следовательно, по определению, (k∙a):(k∙b) = c.
Признаки делимости
Если число оканчивается цифрой 0, то оно делится на 10.
Например, число 4560 оканчивается цифрой 0, его можно представить в виде произведения 456∙10, которое делится на 10 (по теореме 1).
Число 4561 не делится на 10, потому что 4561 = 4560+1 – сумма числа 4560, делящегося на 10, и числа 1, не делящегося на 10 (по теореме 4).
Если число оканчивается одной из цифр 0 или 5, то оно делится на 5.
Например, число 2300 делится на 5, потому что это число делится на 10, а 10 делится на 5 (по теореме 2).
Число 2305 оканчивается цифрой 5, оно делится на 5, так как его можно записать в виде суммы чисел, делящихся на 5: 2300 + 5 (по теореме 3).
Число 52 не делится на 5, потому что 52 = 50 + 2 – сумма числа 50, делящегося на 5, и числа 2, не делящегося на 5 (по теореме 4).
Простые и составные числа
Каждое натуральное число р делится на 1 и само на себя:
р:1=р, р:р=1.
Простым числом называют такое натуральное число, которое больше единицы и делится только на 1 и само на себя.
Вот первые десять простых чисел:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Непростые натуральные числа, большие единицы, называют составными. Каждое составное число делится на 1, само на себя и еще хотя бы на одно натуральное число.
Вот все составные числа, меньшие 20:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18.
Принято считать, что единица не является ни простым, ни составным числом.
Таким образом, множество всех натуральных чисел состоит из простых чисел, составных чисел и единицы.
Простых чисел бесконечно много, есть первое число – 2, но нет последнего простого числа.
Делители натурального числа
Если натуральное число а делится на натуральное число b, то число b называют делителем числа а.
Например, делителями числа 13 являются числа 1 и 13, делителями числа 4 – числа 1, 2, 4, а делителями числа 12 – числа 1, 2, 3, 4, 6, 12.
Каждое простое число имеет только два делителя – единицу и само себя, а каждое составное число, кроме единицы и себя, имеет и другие делители.
Если делитель – простое число, то его называют простым делителем. Например, число 13 имеет простой делитель 13, число 4 – простой делитель 2, а число 12 – простые делители 2 и 3.
Каждое составное число можно представить в виде произведения его простых делителей. Например,
28 = 2∙2∙7 = 22∙7;
22 = 2∙11;
81 = 3∙3∙3∙3 = З4;
100 = 2∙2∙5∙5 = 22∙52.
Правые части полученных равенств называют разложением на простые множители чисел 28, 22, 81 и 100.
Разложить данное составное число на простые множители – значит представить его в виде произведения различных его простых делителей или их степеней.
Покажем, как можно разложить число 90 на простые множители.
1) 90 делится на 2, 90:2 = 45;
2) 45 не делится на 2, но делится на 3, 45:3= 15;
3) 15 делится на 3, 15:3 = 5;
4) 5 делится на 5, 5:5 = 1.
Таким образом, 90 = 2∙45 = 2∙3∙15 = 2∙3∙3∙5.
Наибольший общий делитель
Число 12 имеет делители 1, 2, 3, 4, 12. Число 54 имеет делители 1, 2, 3, 6, 9, 18, 27, 54. Мы видим, что числа 12 и 54 имеют общие делители 1, 2, 3, 6.
Наибольшим общим делителем чисел 12 и 54 является число 6.
Наибольший общий делитель чисел а и b обозначают: НОД (а, b).
Например, НОД (12, 54) = 6.
Наименьшее общее кратное
Число, делящееся на 12, называется кратным числу 12. Числу 12 кратны числа 12, 24, 36, 48, 60, 72, 84, 96, 108 и т.д. Числу 18 кратны числа 18, 36, 54, 72, 90, 108, 126 и т. д.
Мы видим, что имеются числа, кратные одновременно 12 и 18. Например, 36, 72, 108,.... Эти числа называются общими кратными чисел 12 и 18.
Наименьшим общим кратным натуральных чисел а и b называют наименьшее натуральное число, делящееся нацело на а и b. Это число обозначают: НОК (а, b).
Наименьшее общее кратное двух чисел обычно находят одним из двух способов. Рассмотрим их.
Найдем НОК(18, 24).
I способ. Будем выписывать числа, кратные 24 (большему из данных чисел), проверяя, делится ли каждое из них на 18: 24∙1=24 – не делится на 18, 24∙2 = 48 – не делится на 18, 24∙3 = 72 – делится на 18, поэтому НОК (24, 18) =
= 72.
II способ. Разложим числа 24 и 18 на простые множители: 24 = 2∙2∙2∙3,
18 = 2∙3∙3.
НОК(24, 18) должно делиться и на 24, и на 18. Поэтому искомое число содержит все простые делители большего числа 24 (т. е. числа 2, 2, 2, 3) и еще недостающие множители из разложения меньшего числа 18 (еще одно число 3). Поэтому НОК(18, 24) = 2∙2∙2∙3∙3 = 72.
Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее кратное равно произведению этих чисел. Например, 24 и 25 – взаимно простые числа. Поэтому НОК (24, 25) = 24∙25 = 600.
Если одно из двух чисел делится нацело на другое, то наименьшее общее кратное этих чисел равно большему из них. Например, 120 делится нацело на 24, следовательно, НОК (120, 24)= 120.
Целые числа [2]
Напоминание. Числа, которые используют при подсчете количества предметов, называют натуральными числами. Нуль не считается натуральным числом. Натуральные числа и нуль, записанные в порядке возрастания и без пропусков, образуют ряд целых неотрицательных чисел:
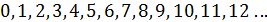
В этой разделе будут введены новые числа – целые отрицательные.
Целые отрицательные числа
Базовый пример из жизни – термометр. Предположим, он показывает температуру 7° тепла. Если температура понизится на 4°, то термометр будет показывать 3° тепла. Уменьшению температуры соответствует действие вычитания: 7 – 4 = 3. Если температура понизится на 7°, то термометр покажет 0°: 7 – 7 = 0.
Если же температура понизится на 8°, то термометр покажет –1° (1° мороза). Но результат вычитания 7 – 8 нельзя записать с помощью натуральных чисел и нуля, хотя он имеет реальный смысл.
Отсчитать в ряду неотрицательных целых чисел от числа 7 влево 8 чисел нельзя. Чтобы действие 7 – 8 стало выполнимым, расширим ряд неотрицательных целых чисел. Для этого влево от нуля запишем (справа налево) по порядку все натуральные числа, добавляя к каждому из них знак «–», показывающий, что это число стоит слева от нуля.
Записи –1, –2, –3,... читают «минус 1», «минус 2», «минус 3» и т. д.:
–5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5,....
Полученный ряд чисел называют рядом целых чисел. Точки слева и справа в этой записи означают, что ряд можно продолжать неограниченно вправо и влево.
Справа от числа 0 в этом ряду расположены числа, которые называют натуральными или целыми положительными.
Сравнение целых чисел
Из двух целых чисел больше то, которое в ряду целых чисел стоит правее.
Если а больше b, то пишут а > b или b < а.
Например, 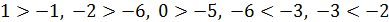 ,
,
так как в ряду целых чисел
..., –6, –5, –4, –3, –2, –1, 0, +1, +2, +3, +4, +5, +6,...
1 правее (–1), (–2) правее (–6) и т. д.
Из правила сравнения целых чисел следует, что любое положительное число больше 0, а любое отрицательное число меньше 0; любое положительное число больше любого отрицательного.
Отрицательные числа удобно сравнивать с помощью их модулей. Так как в ряду целых чисел отрицательное число с большим модулем стоит левее, то из двух отрицательных чисел больше то, у которого модуль меньше.
Например, так как 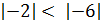 , то
, то 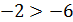 .
.
Если числа а и b не равны друг другу, то пишут: а ≠ b.
Например, 5 ≠ 3, –2 ≠ 0,
Сложение целых чисел
Сумма целых чисел а и b (b ≠ 0) есть целое число с, отстоящее в ряду целых чисел от а на 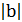 чисел вправо, если b > 0, и влево, если b < 0.
чисел вправо, если b > 0, и влево, если b < 0.
При этом числа а и b называют слагаемыми и пишут:
с=а + b.
Примечание. При а > 0 и b > 0 этим определением мы уже пользовались, когда определяли сложение натуральных чисел.
Пример 1. Определим сумму (+3) + (+8).
Решение. Так как +8 > 0 и 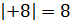 , то от числа +3 в ряду целых чисел отсчитаем вправо 8 чисел и получим число +11.
, то от числа +3 в ряду целых чисел отсчитаем вправо 8 чисел и получим число +11.
Таким образом, (+3) + (+8) = +11.
Пример 2. Определим сумму (–3) + (–8).
Решение. Так как –8 < 0 и 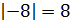 , то от числа –3 в ряду целых чисел отсчитаем влево 8 чисел и получим число –11.
, то от числа –3 в ряду целых чисел отсчитаем влево 8 чисел и получим число –11.
Таким образом, 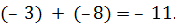
Рассмотренные примеры подтверждают правило: чтобы сложить два числа одинаковых знаков, надо сложить их модули и поставить перед суммой знак слагаемых.
Еще раз подчеркнем, что сумма положительных чисел есть число положительное, а сумма отрицательных чисел есть число отрицательное.
На основании этого правила имеем:
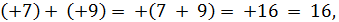
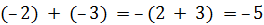 .
.
Пример 3. Определим сумму 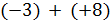 .
.
Решение. Так как +8 > 0 и 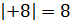 , то от числа –3 в ряду целых чисел отсчитаем вправо 8 чисел и получим число +5.
, то от числа –3 в ряду целых чисел отсчитаем вправо 8 чисел и получим число +5.
Таким образом, (–3) + (+8) = +5.
Заметим, что модуль положительного слагаемого больше модуля отрицательного слагаемого и сумма положительное число, равное 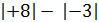 .
.
Пример 4. Определим сумму
Решение. Так как –8 < 0 и 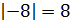 , то от числа +3 в ряду целых чисел отсчитаем влево 8 чисел и получим число –5.
, то от числа +3 в ряду целых чисел отсчитаем влево 8 чисел и получим число –5.
Таким образом, 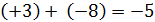 .
.
Здесь модуль отрицательного слагаемого больше модуля положительного слагаемого и сумма отрицательное число, равное 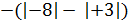 .
.
Рассмотренные примеры подтверждают правило: чтобы сложить два числа разных знаков и с разными модулями, надо из большего модуля вычесть меньший и перед разностью поставить знак слагаемого с большим модулем.
На основании этого правила имеем:
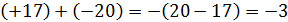 , так как
, так как 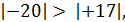
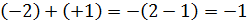 , так как
, так как 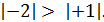
Пример 5. Определим сумму (+5) + (–5).
Решение. Так как –5 < 0 и 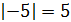 , то от числа (+5) в ряду целых чисел отсчитаем влево 5 чисел, получим число 0.
, то от числа (+5) в ряду целых чисел отсчитаем влево 5 чисел, получим число 0.
Таким образом, (+5) + (–5) = 0.
Этот пример подтверждает правило: сумма противоположных чисел равна нулю.
а + (–а) = 0.
Ha основании этого правила имеем:
(+3) + (–3) = 0, (–7) + (+7) = 0.
Для любого целого числа а:
а + 0 = а, 0 + а = а.
Например, 0 + (–3) = –3; (+5) + 0= + 5; 0 + 0 = 0/
Законы сложения целых чисел
Для любых целых чисел а и b выполняется переместительный закон сложения: сумма двух целых чисел не зависит от порядка слагаемых:
a + b = b + а.
Переместительный закон сложения для целых чисел следует из правил сложения целых чисел и справедливости переместительного закона сложения для натуральных чисел.
Например, суммы –3 + (–5) и –5 + (–3) отрицательные, чтобы найти модуль каждой из этих сумм, надо сложить модули слагаемых: 3 + 5 и 5 + 3, а на основании переместительного закона для натуральных чисел эти суммы равны. Следовательно, – 3+(–5)= –5+(–3).
Для любых целых чисел a, b и с справедлив сочетательный закон сложения: чтобы к сумме двух целых чисел прибавить третье целое число, можно к первому числу прибавить сумму второго и третьего – результат будет тот же:
(а + b) + с = а + (b + с).
Справедливость этого закона следует из правил сложения целых чисел и справедливости сочетательного закона сложения для натуральных чисел.
Например,
(2 + 5) + (–3) = 2 + (5 + (–3)).
В справедливости этих законов можно убедиться и с помощью ряда целых чисел.
С помощью переместительного и сочетательного законов сложения можно показать, что сумму нескольких целых слагаемых:
1) можно записывать без скобок,
2) любые слагаемые в ней можно менять местами,
3) некоторые слагаемые в ней можно заключать в скобки.
Например, верно равенство
a + b + c + k = (c + k) + (a + b).
Докажем это:
a + b + c + k = (a + b + c) + k = k + (a + b + c) = k + ((a + b) + c) =
= k + (c + (a + b)) = (k + c) + (a + b) = (c + k) + (a + b).
Приведенные выше правила применяются для упрощения вычислений. Например, 3 + (–6) + (–4) + 6 + (–5) + 4 = (3 + (–5)) + ((–6) + 6) + (4 + (–4)) =
= –2 + 0 + 0 = –2.
Разность целых чисел
Разностью целых чисел а и b называют такое число а – b, сумма которого с b равна а:
(a – b) + b = a.
Покажем, что разность a – b есть сумма числа а и числа противоположного числу b:
a – b = a + (–b).
Чтобы доказать это, надо найти сумму чисел а + (–b) и b. Применяя сочетательный закон сложения, получаем:
(a + (–b)) + b = a + ((–b)+b) = a + 0 = a.
Таким образом, чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому:
a –b = a + (–b).
Например, –3 – (–5) = –3 + 5 = 2,
2 – 7 = 2 + (–7)= –5,
0 – 5 = 0 +(–5) = –5,
–7 – 2 = –7 + (–2) = –9,
0 – 0 = 0 + (–0) = 0 + 0 = 0.
Отметим, что в множестве натуральных чисел нельзя было из меньшего числа вычесть большее. В множестве целых чисел это возможно. Например,
2 – 7 = 2 + (–7)= –(7 – 2) = –5.
Произведение целых чисел
Произведением двух целых не равных нулю чисел называют произведение их модулей, взятое со знаком «+», если эти числа одинаковых знаков, и со знаком «–», если они разных знаков.
Например, 6∙8 = (+6)∙(+8) = +(6∙8) = +48
(–5)∙(–10) = +(5∙10) =+50,
7∙(–3) = (+7) (–3) = –(7∙3) = –21,
(–5)∙10 = (–5)∙(+10) = –(5∙10) = –50.
Произведение любого целого числа а и нуля равно нулю:
а∙0 = 0,
0∙а = 0.
Например, (+7)∙0 = 0∙(+7) = 0,
(–10)∙0 = 0∙(–10) = 0,
0∙0 = 0.
Переместительный и сочетательный законы умножения верны для любых целых чисел:
a∙b = b∙a, (а∙b)∙с = а∙(b∙с).
Из определения произведения целых чисел и выполнимости переместительного и сочетательного законов умножения для неотрицательных целых чисел следует, что эти законы выполняются и для целых чисел.
Например, (–5)∙(–6) = +(5∙6) =+ (6∙5) = (–6)∙(–5),
((+5)∙(–3))∙(–4) = (–(5∙3)∙(–4)=+((5∙3)∙4) = = +(5∙(3∙4)) = (+5)∙((–3)∙(–4)).
Отметим, что при умножении любого целого числа а на (– 1), меняется только его знак, т. е. получается противоположное ему число:
(–1)∙а = –а.
Например, (–1)∙(+5) = –5, (–1)∙(–5)= +5.
Частное целых чисел
Пусть а и b целые числа, не равные нулю, такие, что 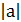 делится нацело на
делится нацело на 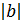 , тогда частное чисел а и b равно частному их модулей, взятому со знаком «+», если эти числа одинаковых знаков, и со знаком «–», если они разных знаков.
, тогда частное чисел а и b равно частному их модулей, взятому со знаком «+», если эти числа одинаковых знаков, и со знаком «–», если они разных знаков.
Например, (–20):(–5)=+(20:5) = 4,
40:5 = 8,
8:(–2) = –(8:2) = –4,
(–12):3 = –(12:3) = –4.
Частное от деления нуля на любое целое, не равное нулю, число а равно нулю: 0:а = 0.
Например, 0:(–5) = 0, 0:3 = 0.
Делить на 0 нельзя.
Замечание. Так же как и для натуральных чисел, деление нацело целых отличных от нуля чисел не всегда возможно. В следующем разделе будут рассмотрены новые – рациональные числа и тогда любое целое число можно будет разделить на любое отличное от нуля целое число.
Исторические сведения
Впервые отрицательные числа встречаются в одной из книг «Математика в девяти книгах» (Джань Дань, III в. до н. э., Китай). Отрицательное число тогда понималось как долг, а положительное – как имущество. Сложение и вычитание отрицательных чисел производилось на основе рассуждений о долге. Например, правило сложения формулировалось так: «Если к одному долгу прибавить другой долг, то в результате получится долг, а не имущество». Знака «минус» тогда не было, а чтобы отличать положительные и отрицательные числа, Джань Цань писал их чернилами разных цветов.
Древнегреческий ученый Диофант (III в.) свободно оперировал отрицательными числами. Они постоянно встречаются в промежуточных вычислениях во многих задачах его «Арифметики». Например, правило умножения с отрицательными числами он формулировал так: «Вычитаемое, умноженное на вычитаемое, дает прибавляемое, а вычитаемое, умноженное на прибавляемое, дает вычитаемое».
В VI–VII веках нашей эры индийские математики уже систематически пользовались отрицательными числами, по-прежнему
понимая их как долг. Впервые все четыре арифметических действия с отрицательными числами приведены индийским математиком и астрономом Брамагуптой (598–660). Например, правило деления он формулировал так: «Положительное, деленное на положительное, или отрицательное, деленное на отрицательное, становится положительным. Но положительное, деленное на отрицательное, и отрицательное, деленное на положительное, остается отрицательным».
Независимо от индийцев к пониманию отрицательных чисел, как противоположности положительных, пришел итальянский математик Леонардо Пизанский (Фибоначчи) (XIII в.).
Немецкий математик М. Штифель (XVI в.) впервые рассматривал отрицательные числа как числа, меньшие нуля («меньшие чем ничто»).
Однако и в XVI–XVII веках многие европейские математики не признавали отрицательных чисел. Если такие числа встречались в вычислениях, то их называли ложными, невозможными.
Современное толкование отрицательных чисел, основанное на откладывании отрезков на координатной оси влево от нуля, было дано в XVII веке, в основном в работах голландского математика А. Жирара (1595–1632) и знаменитого французского математика и философа Р. Декарта (1596–1650).
Таким образом, для того чтобы разработать современный подход к отрицательным числам, понадобились усилия многих ученых на протяжении 18 веков от Джань Цаня до Декарта.
Дополнительный раздел
Целые числа. Делимость.
В этом разделе изложены классические результаты элементарной теории чисел – лемма Евклида, основная теорема элементарной теории чисел (основная теорема арифметики), алгоритм Евклида для вычисления наибольшего общего делителя и наименьшего общего кратного, соотношение Безу. На этой основе получены признаки делимости целых чисел с остатками. Данный обзор подготовлен по материалам работ:
1. Жиков В.В. Основная теорема арифметики // Соросовский образовательный журнал. – 2000. – Т. 6. – № 3. – С. 112 – 117.
2. Калужнин Л.А. Основная теорема арифметики. – М.: Наука, 1969. – 32 с.
3. Основная теорема арифметики // Материал из Википедии – свободной энциклопедии. – http://ru.wikipedia.org/wiki/
Теорема Евклида – классический результат элементарной теории чисел. Она сформулирована как предложение 30 в книге VII «Начал» Евклида.
Если простое число p делит без остатка произведение двух целых чисел 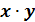 , то p делит
, то p делит 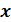 или
или 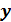 .
.
Доказательство
Пусть 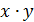 делится на
делится на 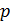 , но
, но 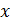 не делится на
не делится на 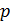 . Тогда
. Тогда 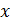 и
и 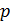 – взаимно простые, следовательно, найдутся целые числа u и v такие, что
– взаимно простые, следовательно, найдутся целые числа u и v такие, что
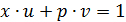 (соотношение Безу).
(соотношение Безу).
Умножая обе части на y, получаем
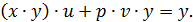
Оба слагаемых в левой части делятся на 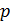 , значит, и правая часть делится на
, значит, и правая часть делится на 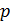 , ч.т.д.
, ч.т.д.
Замечание 1. К этому доказательству теоремы Евклида нужно еще присоединить доказательство использованного здесь соотношения Безу, оно будет дано позже.
Замечание 2. Ниже будет также показано, что из этой теоремы Евклида легко выводится свойство единственности разложения натурального числа в произведение простых множителей. Само это свойство единственности в «Началах» не сформулировано и, вероятно, поэтому в течение веков рассматривалось как самоочевидный факт. К.Ф. Гаусс первый отметил, что невозможность двух существенно различных разложений одного и того же числа на простые множители вовсе не очевидна и нуждается в доказательстве. Он же сформулировал и доказал в 1801 году следующую основную теорему арифметики:
Всякое натуральное число больше единицы либо само является простым числом, либо его можно представить в виде произведения простых множителей, и это представление единственно (с точностью до порядка множителей).
Доказательство Евклида разложения на простые множители.
Начнем со следующей леммы Евклида:
Всякое целое число n > 1 имеет простой делитель.
Доказательство. Среди делителей числа n имеются числа, превосходящие 1 (например, само число n). Пусть p – наименьший из таких его делителей. Очевидно, что р есть простое число, ибо иначе оно имело бы такой делитель u, что 1 < u < р. Но u, будучи делителем р, было бы и делителем числа n, что противоречит определению числа р, и лемма доказана.
Теперь для 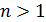 по лемме Евклида имеем
по лемме Евклида имеем 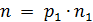 , где
, где 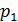 – простое число. Если
– простое число. Если 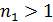 , то снова по лемме Евклида
, то снова по лемме Евклида 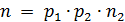 , где
, где 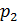 – тоже простое число. Поскольку
– тоже простое число. Поскольку 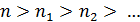 , то за конечное число шагов получим
, то за конечное число шагов получим 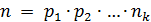 и все множители справа простые. Разложение на простые делители доказано.
и все множители справа простые. Разложение на простые делители доказано.
История
Древнегреческие математики называли этот алгоритм ἀνθυφαίρεσις или ἀνταναίρεσις – «взаимное вычитание». Этот алгоритм не был открыт Евклидом, так как упоминание о нём имеется уже в Топике Аристотеля. В «Началах» Евклида он описан дважды – в VII книге для нахождения наибольшего общего делителя двух натуральных чисел и в X книге для нахождения наибольшей общей меры двух однородных величин. В обоих случаях дано геометрическое описание алгоритма, для нахождения «общей меры» двух отрезков.
Историками математики (Цейтен и др.) было выдвинуто предположение, что именно с помощью алгоритма Евклида (процедуры последовательного взаимного вычитания) в древнегреческой математике впервые было открыто существование несоизмеримых величин (стороны и диагонали квадрата, или стороны и диагонали правильного пятиугольника). Впрочем, это предположение не имеет достаточных документальных подтверждений. Алгоритм для поиска наибольшего общего делителя двух натуральных чисел описан также в I книге древнекитайского трактата Математика в девяти книгах.
Ряд математиков средневекового Востока (Сабит ибн Курра, ал-Махани, Ибн ал-Хайсам, Омар Хайям) попытались построить на основе алгоритма Евклида теорию отношений, альтернативную по отношению теории отношений Евдокса, изложенной в V книге «Начал» Евклида. Согласно определению, предложенному этими авторами, четыре величины, первая ко второй и третья к четвёртой, имеют между собой одно и то же отношение, если при последовательном взаимном вычитании второй величины в обеих парах на каждом шаге будут получаться одни и те же неполные частные.
Пример
Для иллюстрации, алгоритм Евклида будет использован, чтобы найти  , для a = 1071 и b = 462. Сначала от 1071 нужно отнимать 462 до тех пор, пока не получим число, меньшее 462. В данном случае эту операцию нужно проделать дважды, следовательно, q 1 = 2, остаток
, для a = 1071 и b = 462. Сначала от 1071 нужно отнимать 462 до тех пор, пока не получим число, меньшее 462. В данном случае эту операцию нужно проделать дважды, следовательно, q 1 = 2, остаток 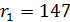 .
.
1071 = 2 ∙ 462 + 147.
Затем от 462 отнимем число кратное 147 так, чтобы разность была меньше чем 147. q 2 = 3, остаток 21.
462 = 3 147 + 21.
Далее 147 = 7 ∙ 21 + 0.
Так как последний остаток равен нулю, алгоритм заканчивается и НОД(1071, 462) = 21.
Подобные слагаемые
Для любых чисел а, b и с верны равенства:

| (1)
|

| (2)
|

| (3)
|

| (4)
|
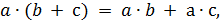
| (5)
|

| (6)
|

| (7)
|

| (8)
|

| (9)
|

| (10)
|

| (11)
|
С помощью этих равенств можно упрощать буквенные выражения. Например,  .
.
Слагаемые  содержат одинаковые буквенные множители. Такие слагаемые называют подобными. Числовой множитель в произведении вида 7х называют коэффициентом.
содержат одинаковые буквенные множители. Такие слагаемые называют подобными. Числовой множитель в произведении вида 7х называют коэффициентом.
Пользуясь распределительным законом, можно упрощать выражения, содержащие подобные слагаемые. Например, упростим выражения:


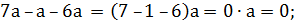
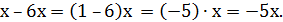
Такое упрощение выражений называют приведением подобных слагаемых. Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученное число умножить на общий буквенный множитель.
В простых случаях промежуточные вычисления опускают, например, пишут:  .
.
Если слагаемых больше двух, то при приведении подобных слагаемых бывает полезно группировать отдельно слагаемые с коэффициентами разных знаков.
Например, 

[1] Здесь представлен краткий конспект соответствующих разделов учебника: Арифметика, 5 / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 1999. – 255 с. Нумерация разделов такая же, как и в учебнике.
[2] Краткий конспект по данной теме составлен на основании соответствующих разделов учебника: Арифметика, 6 / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2000. – 270 с.
Тематические обзоры по курсу элементарной математики
Составитель В.Г.Ермаков
Тема I. Числовые системы
1. Натуральные числа [1]
Ряд натуральных чисел
Еще в глубокой древности потребности обмена, торговли, скотоводства и т. п. привели людей к нео






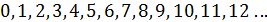
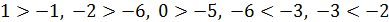 ,
,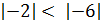 , то
, то 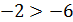 .
.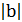 чисел вправо, если b > 0, и влево, если b < 0.
чисел вправо, если b > 0, и влево, если b < 0.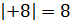 , то от числа +3 в ряду целых чисел отсчитаем вправо 8 чисел и получим число +11.
, то от числа +3 в ряду целых чисел отсчитаем вправо 8 чисел и получим число +11.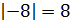 , то от числа –3 в ряду целых чисел отсчитаем влево 8 чисел и получим число –11.
, то от числа –3 в ряду целых чисел отсчитаем влево 8 чисел и получим число –11.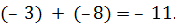
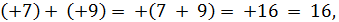
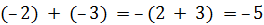 .
.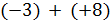 .
.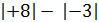 .
.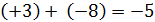 .
.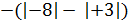 .
.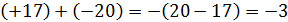 , так как
, так как 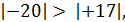
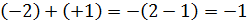 , так как
, так как 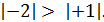
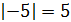 , то от числа (+5) в ряду целых чисел отсчитаем влево 5 чисел, получим число 0.
, то от числа (+5) в ряду целых чисел отсчитаем влево 5 чисел, получим число 0.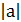 делится нацело на
делится нацело на 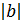 , тогда частное чисел а и b равно частному их модулей, взятому со знаком «+», если эти числа одинаковых знаков, и со знаком «–», если они разных знаков.
, тогда частное чисел а и b равно частному их модулей, взятому со знаком «+», если эти числа одинаковых знаков, и со знаком «–», если они разных знаков.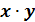 , то p делит
, то p делит 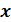 или
или 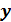 .
.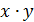 делится на
делится на 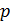 , но
, но 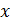 не делится на
не делится на 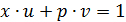 (соотношение Безу).
(соотношение Безу).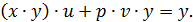
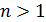 по лемме Евклида имеем
по лемме Евклида имеем 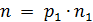 , где
, где 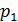 – простое число. Если
– простое число. Если 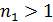 , то снова по лемме Евклида
, то снова по лемме Евклида 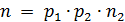 , где
, где 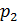 – тоже простое число. Поскольку
– тоже простое число. Поскольку 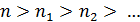 , то за конечное число шагов получим
, то за конечное число шагов получим 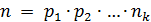 и все множители справа простые. Разложение на простые делители доказано.
и все множители справа простые. Разложение на простые делители доказано. , для a = 1071 и b = 462. Сначала от 1071 нужно отнимать 462 до тех пор, пока не получим число, меньшее 462. В данном случае эту операцию нужно проделать дважды, следовательно, q 1 = 2, остаток
, для a = 1071 и b = 462. Сначала от 1071 нужно отнимать 462 до тех пор, пока не получим число, меньшее 462. В данном случае эту операцию нужно проделать дважды, следовательно, q 1 = 2, остаток 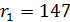 .
.



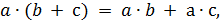






 .
. содержат одинаковые буквенные множители. Такие слагаемые называют подобными. Числовой множитель в произведении вида 7х называют коэффициентом.
содержат одинаковые буквенные множители. Такие слагаемые называют подобными. Числовой множитель в произведении вида 7х называют коэффициентом.

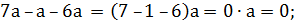
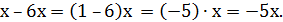
 .
.




