Число 0 не является ни положительным, ни отрицательным числом. Оно разделяет положительные и отрицательные числа.
Таким образом, ряд целых чисел образуют натуральные числа, целые отрицательные числа и число нуль.
Противоположные числа. Модуль числа
Считают, что если перед целым числом поставить знак «+», то это не изменяет самого числа.
Например, число 5 можно записать как +5, число –5 как +(–5).
5= +5, –5=+(–5).
Поэтому ряд целых чисел можно записать в виде:
–5, –4, –3, –2, –1, 0, +1, +2, +3, +4, +5,....
Числа, которые отличаются только знаком, называют противоположными.
Например, +1 и –1, –5 и +5, +10 и –10 – противоположные числа.
Если перед целым числом поставить знак «–», то получится число, ему противоположное:
–(+1) = –1, –(–2) = +2.
Нуль считается противоположным самому себе: 0 = –0 = +0.
Число, противоположное числу а, обозначают –а. Заметим, что –а может быть положительным, отрицательным или нулем. Например, если а = + 2, то
–а = –2, так как –(+2) = –2; если а = –3, то –а=+3, так как –(–3)= +3; если а = 0, то –а = 0, так как –0 = 0.
Введем понятие модуля, или абсолютной величины числа.
Модулем положительного числа называют само это число.
Например, модулем числа +3 является число +3, пишут:
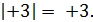
Модулем отрицательного числа называют противоположное ему (положительное) число.
Например, модулем числа –4 является число +4, пишут:
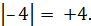
Таким образом, модуль целого, отличного от нуля числа есть положительное число.
Противоположные числа имеют одинаковый модуль: 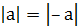 .
.
Например, 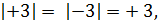
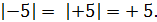
Модулем числа 0 является число 0, пишут:
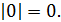
Сравнение целых чисел
Из двух целых чисел больше то, которое в ряду целых чисел стоит правее.
Если а больше b, то пишут а > b или b < а.
Например, 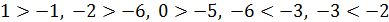 ,
,
так как в ряду целых чисел
..., –6, –5, –4, –3, –2, –1, 0, +1, +2, +3, +4, +5, +6,...
1 правее (–1), (–2) правее (–6) и т. д.
Из правила сравнения целых чисел следует, что любое положительное число больше 0, а любое отрицательное число меньше 0; любое положительное число больше любого отрицательного.
Отрицательные числа удобно сравнивать с помощью их модулей. Так как в ряду целых чисел отрицательное число с большим модулем стоит левее, то из двух отрицательных чисел больше то, у которого модуль меньше.
Например, так как 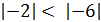 , то
, то 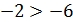 .
.
Если числа а и b не равны друг другу, то пишут: а ≠ b.
Например, 5 ≠ 3, –2 ≠ 0,
Сложение целых чисел
Сумма целых чисел а и b (b ≠ 0) есть целое число с, отстоящее в ряду целых чисел от а на 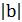 чисел вправо, если b > 0, и влево, если b < 0.
чисел вправо, если b > 0, и влево, если b < 0.
При этом числа а и b называют слагаемыми и пишут:
с=а + b.
Примечание. При а > 0 и b > 0 этим определением мы уже пользовались, когда определяли сложение натуральных чисел.
Пример 1. Определим сумму (+3) + (+8).
Решение. Так как +8 > 0 и 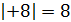 , то от числа +3 в ряду целых чисел отсчитаем вправо 8 чисел и получим число +11.
, то от числа +3 в ряду целых чисел отсчитаем вправо 8 чисел и получим число +11.
Таким образом, (+3) + (+8) = +11.
Пример 2. Определим сумму (–3) + (–8).
Решение. Так как –8 < 0 и 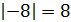 , то от числа –3 в ряду целых чисел отсчитаем влево 8 чисел и получим число –11.
, то от числа –3 в ряду целых чисел отсчитаем влево 8 чисел и получим число –11.
Таким образом, 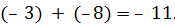
Рассмотренные примеры подтверждают правило: чтобы сложить два числа одинаковых знаков, надо сложить их модули и поставить перед суммой знак слагаемых.
Еще раз подчеркнем, что сумма положительных чисел есть число положительное, а сумма отрицательных чисел есть число отрицательное.
На основании этого правила имеем:
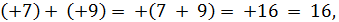
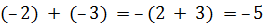 .
.
Пример 3. Определим сумму 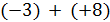 .
.
Решение. Так как +8 > 0 и 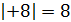 , то от числа –3 в ряду целых чисел отсчитаем вправо 8 чисел и получим число +5.
, то от числа –3 в ряду целых чисел отсчитаем вправо 8 чисел и получим число +5.
Таким образом, (–3) + (+8) = +5.
Заметим, что модуль положительного слагаемого больше модуля отрицательного слагаемого и сумма положительное число, равное 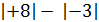 .
.
Пример 4. Определим сумму
Решение. Так как –8 < 0 и 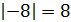 , то от числа +3 в ряду целых чисел отсчитаем влево 8 чисел и получим число –5.
, то от числа +3 в ряду целых чисел отсчитаем влево 8 чисел и получим число –5.
Таким образом, 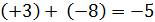 .
.
Здесь модуль отрицательного слагаемого больше модуля положительного слагаемого и сумма отрицательное число, равное 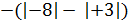 .
.
Рассмотренные примеры подтверждают правило: чтобы сложить два числа разных знаков и с разными модулями, надо из большего модуля вычесть меньший и перед разностью поставить знак слагаемого с большим модулем.
На основании этого правила имеем:
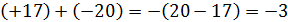 , так как
, так как 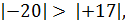
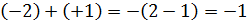 , так как
, так как 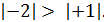
Пример 5. Определим сумму (+5) + (–5).
Решение. Так как –5 < 0 и 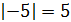 , то от числа (+5) в ряду целых чисел отсчитаем влево 5 чисел, получим число 0.
, то от числа (+5) в ряду целых чисел отсчитаем влево 5 чисел, получим число 0.
Таким образом, (+5) + (–5) = 0.
Этот пример подтверждает правило: сумма противоположных чисел равна нулю.
а + (–а) = 0.
Ha основании этого правила имеем:
(+3) + (–3) = 0, (–7) + (+7) = 0.
Для любого целого числа а:
а + 0 = а, 0 + а = а.
Например, 0 + (–3) = –3; (+5) + 0= + 5; 0 + 0 = 0/
Законы сложения целых чисел
Для любых целых чисел а и b выполняется переместительный закон сложения: сумма двух целых чисел не зависит от порядка слагаемых:
a + b = b + а.
Переместительный закон сложения для целых чисел следует из правил сложения целых чисел и справедливости переместительного закона сложения для натуральных чисел.
Например, суммы –3 + (–5) и –5 + (–3) отрицательные, чтобы найти модуль каждой из этих сумм, надо сложить модули слагаемых: 3 + 5 и 5 + 3, а на основании переместительного закона для натуральных чисел эти суммы равны. Следовательно, – 3+(–5)= –5+(–3).
Для любых целых чисел a, b и с справедлив сочетательный закон сложения: чтобы к сумме двух целых чисел прибавить третье целое число, можно к первому числу прибавить сумму второго и третьего – результат будет тот же:
(а + b) + с = а + (b + с).
Справедливость этого закона следует из правил сложения целых чисел и справедливости сочетательного закона сложения для натуральных чисел.
Например,
(2 + 5) + (–3) = 2 + (5 + (–3)).
В справедливости этих законов можно убедиться и с помощью ряда целых чисел.
С помощью переместительного и сочетательного законов сложения можно показать, что сумму нескольких целых слагаемых:
1) можно записывать без скобок,
2) любые слагаемые в ней можно менять местами,
3) некоторые слагаемые в ней можно заключать в скобки.
Например, верно равенство
a + b + c + k = (c + k) + (a + b).
Докажем это:
a + b + c + k = (a + b + c) + k = k + (a + b + c) = k + ((a + b) + c) =
= k + (c + (a + b)) = (k + c) + (a + b) = (c + k) + (a + b).
Приведенные выше правила применяются для упрощения вычислений. Например, 3 + (–6) + (–4) + 6 + (–5) + 4 = (3 + (–5)) + ((–6) + 6) + (4 + (–4)) =
= –2 + 0 + 0 = –2.
Разность целых чисел
Разностью целых чисел а и b называют такое число а – b, сумма которого с b равна а:
(a – b) + b = a.
Покажем, что разность a – b есть сумма числа а и числа противоположного числу b:
a – b = a + (–b).
Чтобы доказать это, надо найти сумму чисел а + (–b) и b. Применяя сочетательный закон сложения, получаем:
(a + (–b)) + b = a + ((–b)+b) = a + 0 = a.
Таким образом, чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому:
a –b = a + (–b).
Например, –3 – (–5) = –3 + 5 = 2,
2 – 7 = 2 + (–7)= –5,
0 – 5 = 0 +(–5) = –5,
–7 – 2 = –7 + (–2) = –9,
0 – 0 = 0 + (–0) = 0 + 0 = 0.
Отметим, что в множестве натуральных чисел нельзя было из меньшего числа вычесть большее. В множестве целых чисел это возможно. Например,
2 – 7 = 2 + (–7)= –(7 – 2) = –5.
Произведение целых чисел
Произведением двух целых не равных нулю чисел называют произведение их модулей, взятое со знаком «+», если эти числа одинаковых знаков, и со знаком «–», если они разных знаков.
Например, 6∙8 = (+6)∙(+8) = +(6∙8) = +48
(–5)∙(–10) = +(5∙10) =+50,
7∙(–3) = (+7) (–3) = –(7∙3) = –21,
(–5)∙10 = (–5)∙(+10) = –(5∙10) = –50.
Произведение любого целого числа а и нуля равно нулю:
а∙0 = 0,
0∙а = 0.
Например, (+7)∙0 = 0∙(+7) = 0,
(–10)∙0 = 0∙(–10) = 0,
0∙0 = 0.
Переместительный и сочетательный законы умножения верны для любых целых чисел:
a∙b = b∙a, (а∙b)∙с = а∙(b∙с).
Из определения произведения целых чисел и выполнимости переместительного и сочетательного законов умножения для неотрицательных целых чисел следует, что эти законы выполняются и для целых чисел.
Например, (–5)∙(–6) = +(5∙6) =+ (6∙5) = (–6)∙(–5),
((+5)∙(–3))∙(–4) = (–(5∙3)∙(–4)=+((5∙3)∙4) = = +(5∙(3∙4)) = (+5)∙((–3)∙(–4)).
Отметим, что при умножении любого целого числа а на (– 1), меняется только его знак, т. е. получается противоположное ему число:
(–1)∙а = –а.
Например, (–1)∙(+5) = –5, (–1)∙(–5)= +5.
Частное целых чисел
Пусть а и b целые числа, не равные нулю, такие, что 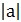 делится нацело на
делится нацело на 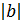 , тогда частное чисел а и b равно частному их модулей, взятому со знаком «+», если эти числа одинаковых знаков, и со знаком «–», если они разных знаков.
, тогда частное чисел а и b равно частному их модулей, взятому со знаком «+», если эти числа одинаковых знаков, и со знаком «–», если они разных знаков.
Например, (–20):(–5)=+(20:5) = 4,
40:5 = 8,
8:(–2) = –(8:2) = –4,
(–12):3 = –(12:3) = –4.
Частное от деления нуля на любое целое, не равное нулю, число а равно нулю: 0:а = 0.
Например, 0:(–5) = 0, 0:3 = 0.
Делить на 0 нельзя.
Замечание. Так же как и для натуральных чисел, деление нацело целых отличных от нуля чисел не всегда возможно. В следующем разделе будут рассмотрены новые – рациональные числа и тогда любое целое число можно будет разделить на любое отличное от нуля целое число.
Исторические сведения
Впервые отрицательные числа встречаются в одной из книг «Математика в девяти книгах» (Джань Дань, III в. до н. э., Китай). Отрицательное число тогда понималось как долг, а положительное – как имущество. Сложение и вычитание отрицательных чисел производилось на основе рассуждений о долге. Например, правило сложения формулировалось так: «Если к одному долгу прибавить другой долг, то в результате получится долг, а не имущество». Знака «минус» тогда не было, а чтобы отличать положительные и отрицательные числа, Джань Цань писал их чернилами разных цветов.
Древнегреческий ученый Диофант (III в.) свободно оперировал отрицательными числами. Они постоянно встречаются в промежуточных вычислениях во многих задачах его «Арифметики». Например, правило умножения с отрицательными числами он формулировал так: «Вычитаемое, умноженное на вычитаемое, дает прибавляемое, а вычитаемое, умноженное на прибавляемое, дает вычитаемое».
В VI–VII веках нашей эры индийские математики уже систематически пользовались отрицательными числами, по-прежнему
понимая их как долг. Впервые все четыре арифметических действия с отрицательными числами приведены индийским математиком и астрономом Брамагуптой (598–660). Например, правило деления он формулировал так: «Положительное, деленное на положительное, или отрицательное, деленное на отрицательное, становится положительным. Но положительное, деленное на отрицательное, и отрицательное, деленное на положительное, остается отрицательным».
Независимо от индийцев к пониманию отрицательных чисел, как противоположности положительных, пришел итальянский математик Леонардо Пизанский (Фибоначчи) (XIII в.).
Немецкий математик М. Штифель (XVI в.) впервые рассматривал отрицательные числа как числа, меньшие нуля («меньшие чем ничто»).
Однако и в XVI–XVII веках многие европейские математики не признавали отрицательных чисел. Если такие числа встречались в вычислениях, то их называли ложными, невозможными.
Современное толкование отрицательных чисел, основанное на откладывании отрезков на координатной оси влево от нуля, было дано в XVII веке, в основном в работах голландского математика А. Жирара (1595–1632) и знаменитого французского математика и философа Р. Декарта (1596–1650).
Таким образом, для того чтобы разработать современный подход к отрицательным числам, понадобились усилия многих ученых на протяжении 18 веков от Джань Цаня до Декарта.
Дополнительный раздел
Целые числа. Делимость.
В этом разделе изложены классические результаты элементарной теории чисел – лемма Евклида, основная теорема элементарной теории чисел (основная теорема арифметики), алгоритм Евклида для вычисления наибольшего общего делителя и наименьшего общего кратного, соотношение Безу. На этой основе получены признаки делимости целых чисел с остатками. Данный обзор подготовлен по материалам работ:
1. Жиков В.В. Основная теорема арифметики // Соросовский образовательный журнал. – 2000. – Т. 6. – № 3. – С. 112 – 117.
2. Калужнин Л.А. Основная теорема арифметики. – М.: Наука, 1969. – 32 с.
3. Основная теорема арифметики // Материал из Википедии – свободной энциклопедии. – http://ru.wikipedia.org/wiki/
Теорема Евклида – классический результат элементарной теории чисел. Она сформулирована как предложение 30 в книге VII «Начал» Евклида.
Если простое число p делит без остатка произведение двух целых чисел 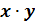 , то p делит
, то p делит 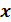 или
или 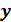 .
.
Доказательство
Пусть 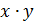 делится на
делится на 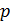 , но
, но 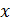 не делится на
не делится на 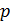 . Тогда
. Тогда 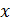 и
и 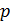 – взаимно простые, следовательно, найдутся целые числа u и v такие, что
– взаимно простые, следовательно, найдутся целые числа u и v такие, что
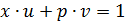 (соотношение Безу).
(соотношение Безу).
Умножая обе части на y, получаем
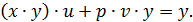
Оба слагаемых в левой части делятся на 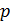 , значит, и правая часть делится на
, значит, и правая часть делится на 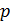 , ч.т.д.
, ч.т.д.
Замечание 1. К этому доказательству теоремы Евклида нужно еще присоединить доказательство использованного здесь соотношения Безу, оно будет дано позже.
Замечание 2. Ниже будет также показано, что из этой теоремы Евклида легко выводится свойство единственности разложения натурального числа в произведение простых множителей. Само это свойство единственности в «Началах» не сформулировано и, вероятно, поэтому в течение веков рассматривалось как самоочевидный факт. К.Ф. Гаусс первый отметил, что невозможность двух существенно различных разложений одного и того же числа на простые множители вовсе не очевидна и нуждается в доказательстве. Он же сформулировал и доказал в 1801 году следующую основную теорему арифметики:
Всякое натуральное число больше единицы либо само является простым числом, либо его можно представить в виде произведения простых множителей, и это представление единственно (с точностью до порядка множителей).
Доказательство Евклида разложения на простые множители.
Начнем со следующей леммы Евклида:
Всякое целое число n > 1 имеет простой делитель.
Доказательство. Среди делителей числа n имеются числа, превосходящие 1 (например, само число n). Пусть p – наименьший из таких его делителей. Очевидно, что р есть простое число, ибо иначе оно имело бы такой делитель u, что 1 < u < р. Но u, будучи делителем р, было бы и делителем числа n, что противоречит определению числа р, и лемма доказана.
Теперь для 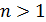 по лемме Евклида имеем
по лемме Евклида имеем 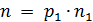 , где
, где 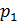 – простое число. Если
– простое число. Если 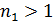 , то снова по лемме Евклида
, то снова по лемме Евклида 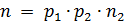 , где
, где 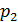 – тоже простое число. Поскольку
– тоже простое число. Поскольку 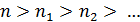 , то за конечное число шагов получим
, то за конечное число шагов получим 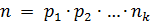 и все множители справа простые. Разложение на простые делители доказано.
и все множители справа простые. Разложение на простые делители доказано.





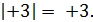
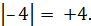
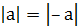 .
.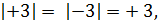
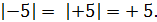
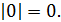
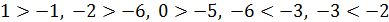 ,
,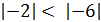 , то
, то 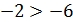 .
.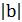 чисел вправо, если b > 0, и влево, если b < 0.
чисел вправо, если b > 0, и влево, если b < 0.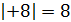 , то от числа +3 в ряду целых чисел отсчитаем вправо 8 чисел и получим число +11.
, то от числа +3 в ряду целых чисел отсчитаем вправо 8 чисел и получим число +11.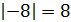 , то от числа –3 в ряду целых чисел отсчитаем влево 8 чисел и получим число –11.
, то от числа –3 в ряду целых чисел отсчитаем влево 8 чисел и получим число –11.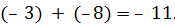
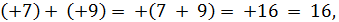
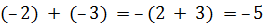 .
.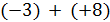 .
.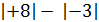 .
.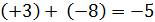 .
.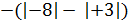 .
.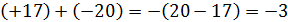 , так как
, так как 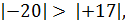
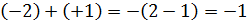 , так как
, так как 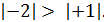
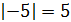 , то от числа (+5) в ряду целых чисел отсчитаем влево 5 чисел, получим число 0.
, то от числа (+5) в ряду целых чисел отсчитаем влево 5 чисел, получим число 0.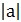 делится нацело на
делится нацело на 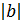 , тогда частное чисел а и b равно частному их модулей, взятому со знаком «+», если эти числа одинаковых знаков, и со знаком «–», если они разных знаков.
, тогда частное чисел а и b равно частному их модулей, взятому со знаком «+», если эти числа одинаковых знаков, и со знаком «–», если они разных знаков.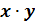 , то p делит
, то p делит 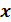 или
или 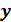 .
.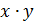 делится на
делится на 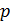 , но
, но 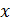 не делится на
не делится на 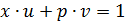 (соотношение Безу).
(соотношение Безу).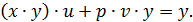
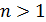 по лемме Евклида имеем
по лемме Евклида имеем 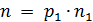 , где
, где 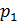 – простое число. Если
– простое число. Если 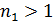 , то снова по лемме Евклида
, то снова по лемме Евклида 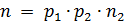 , где
, где 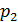 – тоже простое число. Поскольку
– тоже простое число. Поскольку 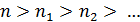 , то за конечное число шагов получим
, то за конечное число шагов получим 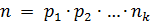 и все множители справа простые. Разложение на простые делители доказано.
и все множители справа простые. Разложение на простые делители доказано.


