Практическое занятие №6. Геометрические характеристики плоских сечений

Знать формулы моментов инерции простейших сечений, спо­собы вычисления моментов инерции при параллельном переносе осей.

Уметь определять полярные и главные центральные моменты инерции для сечений, имеющих ось симметрии.

Моменты инерции простейших сечений

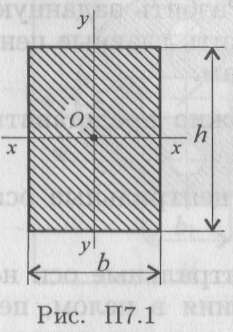
Прямоугольник и квадрат (рис. П7.1)

Осевые:

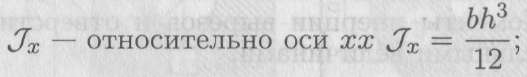
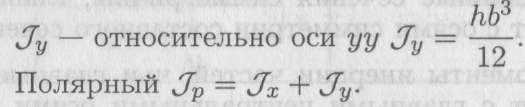
Круг и кольцо (рис. П7.2)

 

где d — диаметр круга и наружный диаметр кольца;

d_BH — внутренний диаметр кольца; с = d_BH/d

 

Моменты инерции относительно параллельных осей (рис. П7.3)

 

 

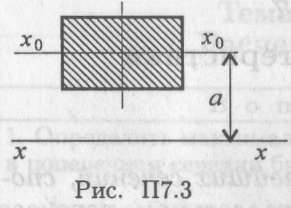
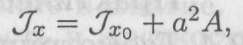
где Jx — момент инерции относительно оси xx,

J_Xo — момент инерции относительно оси х₀х₀;

А — площадь сечения; а — расстояние между осями.

 

Рекомендации для решения задач расчетно-графической работы

1. Момент инерции сложной фигуры является суммой момен­тов инерции частей, на которые ее разбивают. Разбить заданную фигуру на простейшие части, для каждой определить главные цен­тральные моменты инерции по известным формулам.

2. Моменты инерции вырезов и отверстий можно представить отрицательными величинами.

3. Заданные сечения симметричны, главные центральные оси совпадают с осями симметрии составного сечения.

4. Моменты инерции частей, чьи главные центральные оси не совпадают с главными центральными осями сечения в целом, пе­ресчитывают с помощью формулы для моментов инерции относи­тельно параллельных осей. Расстояние между параллельными осями определить по чертежу.

5. При выполнении задания 2 главные центральные моменты инерции отдельных стандартных профилей определить по таблицам ГОСТ (Приложение 1).

Для использованных в составных сечениях полос моменты инер­ции определить по известной формуле для прямоугольника.

Расчетно-графическая работа №8. Определение геометрических характеристик плоских сечений.

 

Геометрические характеристики плоских сечений.

 

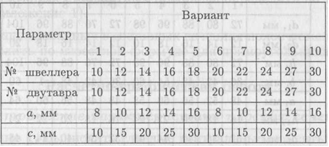
Задание 1. Вычислить главные центральные моменты инерции сечений, представленных на схемах. При расчетах воспользоваться данными таблицы, выбрав необходимые величины (лекция 25, пример 1).

 

 

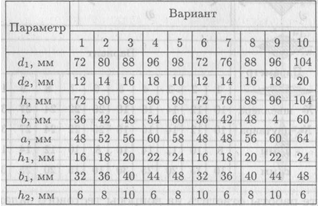
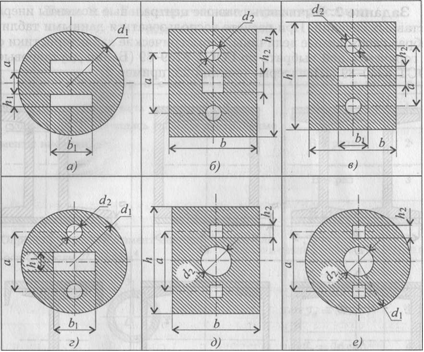
Задание 2. Вычислить главные центральные моменты инерции составных сечений. При расчете воспользоваться данными таблицы, выбрав необходимые величины. Геометрические характеристики ста­ли горячекатаной выбрать по ГОСТ 8239-89 (Балки двутавровые) и ГОСТ 8240-89 (Швеллеры) (лекция 25, пример 2).

 

 

 

 

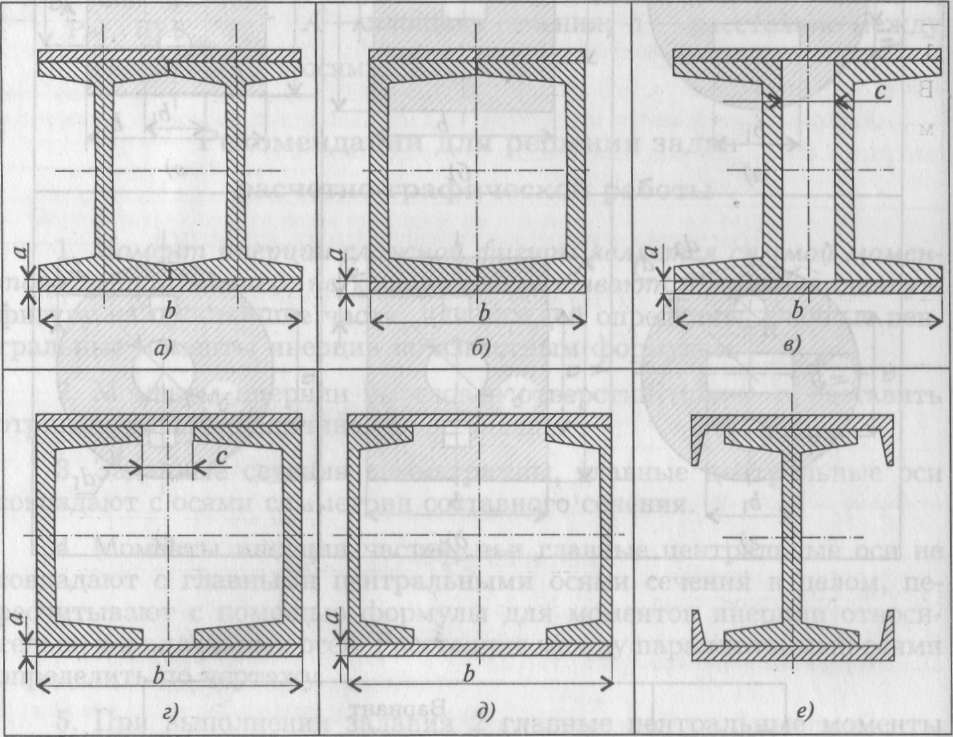
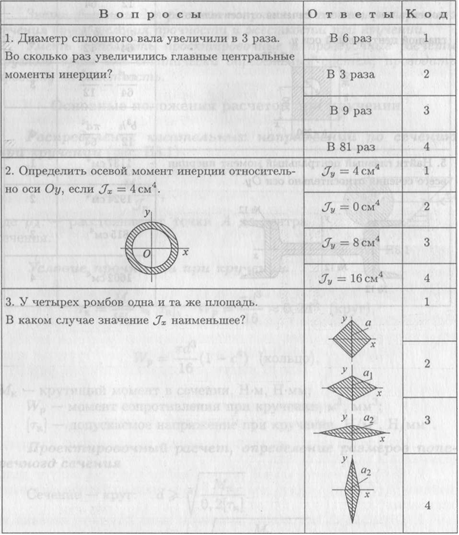
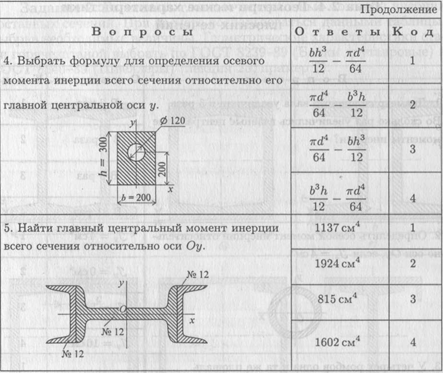
При защите работы ответить на вопросы тестового задания.

Тема 2.4. Геометрические характеристики плоских сечений

 

 

ЛЕКЦИЯ 26

Тема 2.5. Кручение. Внутренние силовые факторы при кручении. Построение эпюр крутящих моментов

Иметь представление о деформациях при кручении, о внутрен­них силовых факторах при кручении.

Уметь строить эпюры крутящих моментов.

Деформации при кручении

 

Кручение круглого бруса происходит при нагружении его пара­ми сил с моментами в плоскостях, перпендикулярных продольной оси. При этом образующие бруса искривляются и разворачиваются на угол γ, называемый углом сдвига (угол поворота образующей). Поперечные сечения разворачиваются на угол ip, называемый углом закручивания (угол поворота сечения, рис. 26.1).

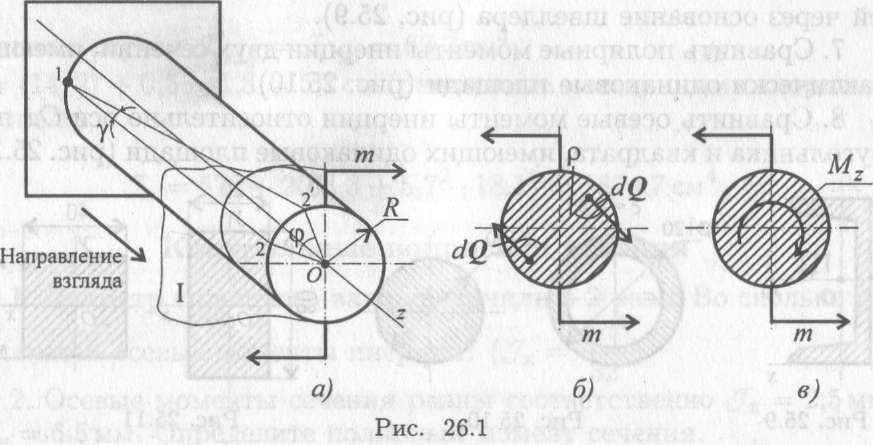Длина бруса и размеры поперечного сечения при кручении не изменяются.

Связь между угловыми деформациями определяется соотноше­нием

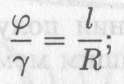
l — длина бруса; R — радиус сечения.

Длина бруса значительно больше радиуса сечения, следователь­но,

φ >> γ.

Угловые деформации при кручении рассчитываются в радиа­нах.

Гипотезы при кручении

 

1. Выполняется гипотеза плоских сечений: поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформа­ции остается плоским и перпендикулярным продольной оси.

2. Радиус, проведенный из центра поперечного сечения бруса, после деформации остается прямой линией (не искривляется).

3. Расстояние между поперечными сечениями после деформа­ции не меняется. Ось бруса не искривляется, диаметры поперечных сечений не меняются.