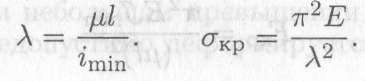История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
Топ:
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Интересное:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Дисциплины:
 2017-07-09 |
 529 |
из
5.00
|
Заказать работу |
|
|
|
|
Относительно короткие и массивные стержни рассчитывают на сжатие, т. к. они выходят из строя в результате разрушения или остаточных деформаций. Длинные стержни небольшого поперечного сечения под действием осевых сжимающих сил изгибаются и теряют равновесие. Такие стержни работают на изгиб и сжатие.
Равновесие считают устойчивым, если за счет сил упругости после снятия внешней отклоняющей силы стержень восстановит первоначальную форму (рис. 36.1).
Если упругое тело после отклонения от равновесного положения не возвращается к исходному состоянию, то говорят, что произошла потеря устойчивости, а равновесие было неустойчивым.
Потерю устойчивости под действием центрально приложенной продольной сжимающей силы называют продольным изгибом.
На устойчивость равновесия влияет величина сжимающей силы.
Наибольшее значение сжимающей силы, при которой прямолинейная форма стержня сохраняет устойчивость, называют критической силой. Даже при небольшом превышении критического значения силы стержень недопустимо деформируется и разрушается.
Расчет на устойчивость
Расчет на устойчивость заключается в определении допускаемой сжимающей силы и в сравнении с ней силы действующей:
где F — действующая сжимающая сила;
[F] — допускаемая сжимающая сила, обеспечивает некоторый запас устойчивости;
FKP — критическая сила;
[sy] — допускаемый коэффициент запаса устойчивости.
Обычно для сталей [sу] = 1,8 – 3; для чугуна [sy] = 5; для дерева [sу] = 2,8.
Способы определения критической силы
Расчет по формуле Эйлера
Задачу определения критической силы математически р решил JI. Эйлер в 1744 г.
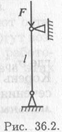
Для шарнирно закрепленного с обеих сторон стержня (рис. 36.2) формула Эйлера имеет вид
|
|
где Е — модуль упругости; лт ^ гт
J min -- минимальный осевой момент инерции стержня;
l — длина стержня.
Потеря устойчивости происходит в плоскости наименьшей жесткости, поэтому в формулу входит минимальный из осевых моментов инерции сечения (Jx или Jy).
Формулу распространили на другие формы закрепления стержней, рассмотрев форму потери устойчивости в каждом случае.
Длина стержня заменяется ее приведенным значением, учитывающим форму потери устойчивости в каждом случае: l ПРИВ = μl, где μ — коэффициент приведения длины, зависящий от способа закрепления стержня (рис. 36.3).
Формула для расчета критической силы для всех случаев
Критические напряжения.
Критическое напряжение — напряжение сжатия, соответствующее критической силе.
Напряжение от сжимающей силы определяется по формуле
где σкр — напряжение сжатия, при котором стержень еще устойчив. Корень квадратный из отношения минимального момента инерции сечения к площади поперечного сечения принято называть минимальным радиусом инерции iт;п:
Тогда формула для расчета критического напряжения перепишется в виде
Отношение μl/i min носит название гибкости стержня λ.
Гибкость стержня — величина безразмерная, чем больше гибкость, тем меньше напряжение:
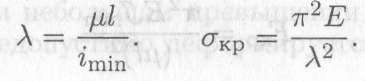
Заметим, что гибкость не зависит от материала, а определяется только геометрией стержня.
|
|
|
Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...
Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!