Структурирование информации с использованием информационных моделей.

Рассмотрим структурирование информации с использованием информационных моделей разного типа.

Наибольшее распространение получили табличные модели, чему в немалой степени способствовала простота их реализации в электронных таблицах.

В табличной модели названия или перечни однотипных объектов или свойств размещают в первой строке (или столбце) таблицы, а значения их свойств — в следующих строках (или столбцах) таблицы.

Столбцы с однотипными данными называют полями, а каждая строка представляет отдельную запись.

Различают таблицы типа «объект — свойство» — когда в одной строке содержится информация об одном объекте или одном событии — и таблицы типа «объект — объект», которые отражают взаимосвязи между разными объектами.

Пример. Разместить в таблицу информацию об осадках и среднесуточной температуре за 5 дней марта.

Однотипные данные будем размещать в столбцах. Поместим в первую строку названия столбцов (полей): Дата, Осадки, Температура. Таблица может выглядеть так:

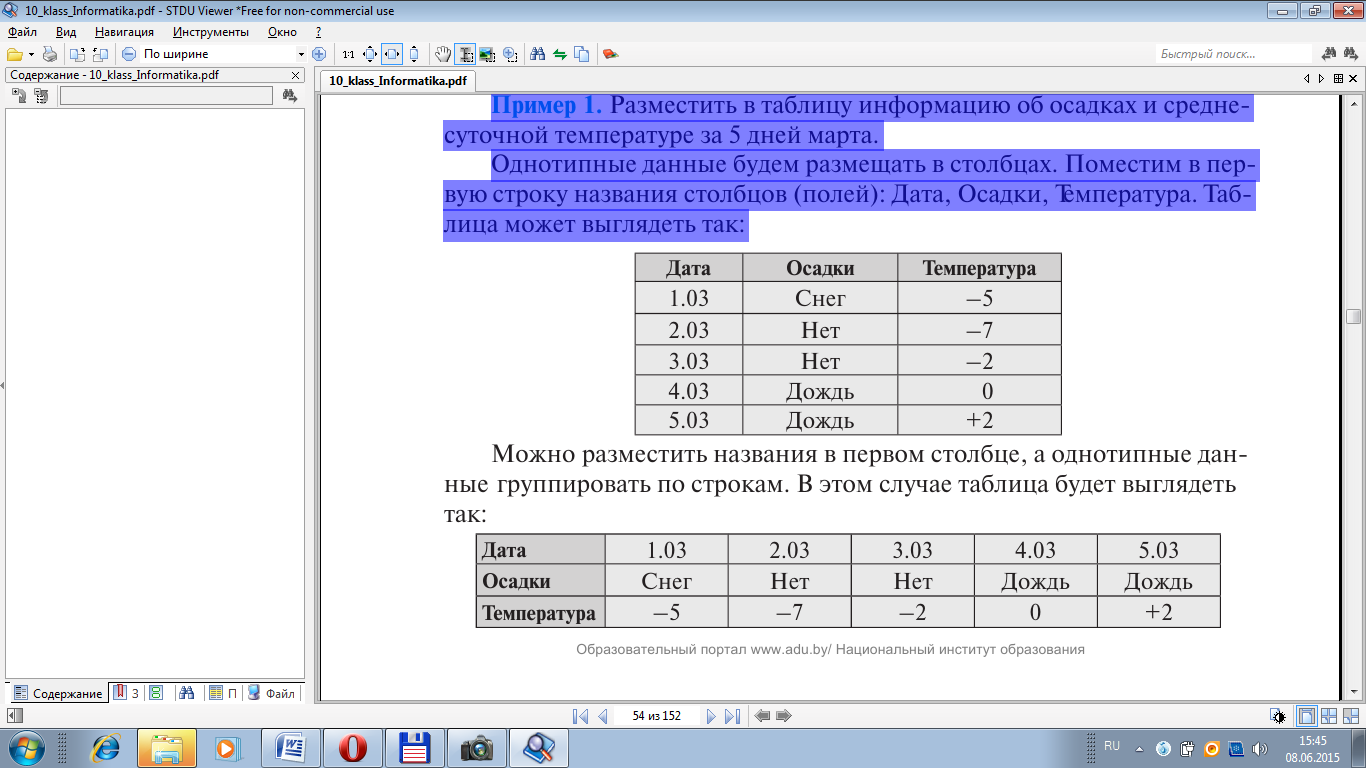
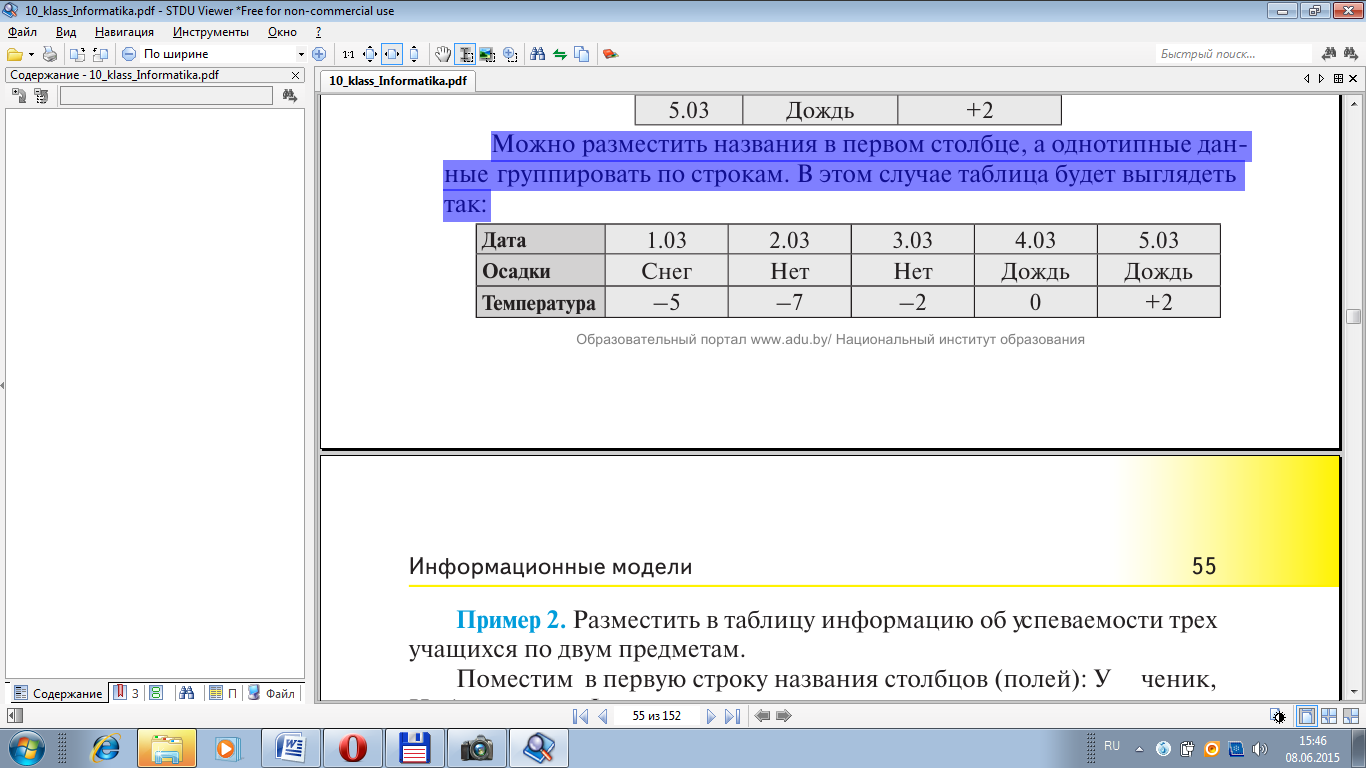
Можно разместить названия в первом столбце, а однотипные данные группировать по строкам. В этом случае таблица будет выглядеть так:

Для наглядного представления состава и структуры данных используют графы. Моделируемые объекты представляют как вершины (или узлы) графа, а связи между объектами — как дуги (или ребра) графа. Получают чертеж, который задает множество вершин и множество линий (связей), соединяющих некоторые пары вершин.

Связи между объектами называются отношениями. Симметричная связь обозначается отрезком, а несимметричная — стрелкой. В ненаправленном графе связи симметричны. В виде такого графа можно представить модель дорог, связывающих населенные пункты:

 

В ориентированном графе отношения между объектами (связи) несимметричны, например: начальник → подчиненный, отец → сын, бабушка → внучка.

Система, объекты которой находятся друг с другом в отношении вложенности или подчиненности, называется иерархической. Иерархическая модель наглядно представляется графом, в котором вершины верхнего уровня связаны с вершинами нижнего уровня как «один ко многим». Примерами иерархических моделей являются графические представления разнообразных классификаций (животных, растений, типов информационных моделей), размещение файлов и папок на жестком диске компьютера и т. п.

Информационная модель, объекты которой (вершины графа различных уровней) связаны между собой по принципу «многие ко многим», называется сетевой. Примерами сетевых моделей могут служить различные сети (компьютеров, магазинов), глобальная сеть Интернет.

С помощью информационных моделей можно представлять знания.

Семантическая модель — модель знаний в форме графа, в основе которой лежит идея о том, что любые знания можно представить в виде совокупности объектов (понятий) и связей (отношений) между ними.

В качестве примера представим в виде графа связи в предложении «Стаіць мая хата між хвой кучаравых».

 

Тема 5 Обработка информации в электронных таблицах

8. Обработка информации в электронных таблицах. Использование стандартных функций для нахождения суммы, среднего арифметического, поиска минимального (максимального) значений.

Функция СУММ

Функция СУММ, вне всяких сомнений, является наиболее используемой функцией Excel. Функция СУММ имеет следующий синтаксис:

СУММ(число1;число2;...;число255)

где число1, число2 — количество аргументов (от 1 до 255), сумму которых необходимо вычислить.

Аргументами функции СУММ должны быть числа, заданные в виде конкретных значений, ссылок на ячейки или диапазоны ячеек, массивов констант. Вместо ссылок можно использовать имена ячеек или диапазонов ячеек. Массив констант представ ляет собой массив чисел, заключенных в фигурные скобки, например {1;2;3} или {1:2:3}. Числа в фигурных скобках должны разделяться точкой с запятой либо двоеточием. Предположим, что в ячейках A1, A2 и A3 содержатся значения 1, 2 и 3. Тогда формулы =СУММ(1;2;3), =СУММ(A1;A2;A3), =СУММ(A1:A3), =СУММ(Данные) и =СУММ({1;2;3}) возвращают один и тот же результат — 6. Здесь имя Данные присвоено диапазону A1:A3. В первой формуле в качестве аргументов функции СУММ используются ссылки на ячейки, во второй формуле аргументом функции СУММ является массив значений.

С помощью функции СУММ можно подсчитать следующее.

· Сумму чисел, содержащихся в одном диапазоне ячеек. В этом случае достаточно задать один аргумент (число1). Для указания ссылки на непрерывный диапазон ячеек используется двоеточие (:) в качестве разделителя между первой и последней ячейками диапазона. Например, формула =СУММ(C5:E5) в ячейке F5 возвращает сумму чисел, содержащихся в диапазоне ячеек C5:E5.

· Сумму чисел, содержащихся в нескольких диапазонах (как смежных, так и нее смежных). В этом случае можно задать до 255 аргументов. Для создания ссылки на два несмежных диапазона используется оператор объединения диапазонов, обозначаемый точкой с запятой (;). Например, формула =СУММ(C5:C7;C9:C11; C13:C15;C17:C19) в ячейке C24 (рис. 6.25) возвращает сумму чисел, которые находятся в диапазонах C5:C7, C9:C11, C13:C15 и C17:C19.

· Сумму чисел, содержащихся в диапазоне, который является пересечением диапазонов, заданных в качестве аргументов. Для создания ссылки на такой диапазон используется оператор пересечения диапазонов — пробел. Например, формула в ячейке C21

=СУММ(C$5:C$7 $C5:$E5;C$9:C$11 $C9:$E9;C$13:C$15 $C13:$E13; C$17:C$19 $C17:$E17)

возвращает сумму чисел, которые содержатся на пересечении диапазонов: C5:C7 и C5:E5 (ячейка C5), C9:C11 и C9:E9 (ячейка C9), C13:C15 и C13:E13 (ячейка C13), C17:C19 и C17:E17 (ячейка C17), т.е. заданная таким образом функция вычисляет сумму чисел, содержащихся в ячейках C5, C9, C13 и C17.

В последней формуле использованы смешанные ссылки на диапазоны. Использование смешанных ссылок позволяет сократить время на ввод достаточно громоздких формул в диапазон C21:E23. Достаточно ввести только одну формулу в ячейку C21 и затем скопировать ее в остальные ячейки диапазона C21:E23.

Если на рабочем листе определены имена, то использование имен в качестве аргументов функции СУММ делает формулы если не менее громоздкими, то, по крайней мере, более осмысленными.

Функция СРЗНАЧ

Функция СРЗНАЧ вычисляет среднее арифметическое своих аргументов. Еслизаданы n действительных чисел a₁, a₂,..., a_n, то число

называется средним арифметическим чисел a₁, a₂,..., a_n.

В формуле для среднего арифметического сначала вычисляется сумма n чисел, затем полученный результат делится на количество слагаемых. Для вычисления среднего арифметического n чисел в Excel можно использовать одну из следующих формул:

· =СРЗНАЧ(Диапазон1)

· =СУММ(Диапазон1)/СЧЁТ(Диапазон1)

Всего функция СРЗНАЧ может иметь до 255 аргументов.

Функции МАКС и МИН

Функция МАКС возвращает наибольшее значение из набора значений, функция МИН — наименьшее значение. В качестве аргументов обеих функций могут использоваться числа, ссылки на ячейки или диапазоны ячеек, имена ячеек или диапазонов, массивы констант. Аргументов может быть до 255.

При определении максимального и минимального значений с помощью функций МАКС и МИН учитываются только те ячейки, которые содержат числа; пустые строки, текст (за исключением чисел, представленных в виде текста) и логические значения игнорируются.

Функции МИН и МАКС возвращают значение ошибки, если хотя бы одна ячейка диапазона содержит значение ошибки. Если диапазон не содержит ячеек с числовыми значениями, функции МАКС и МИН возвращают значение 0 (нуль).

Команды Сумма и Автосумма

Функции СУММ, МИН, МАКС, СРЗНАЧ используются в вычислениях довольно часто. В Excel для быстрой вставки этих функций в формулу на ленте имеются две команды. Команда Сумма расположена на вкладке Главная в группе Редактирование. Команда Автосумма находится на вкладке Формулы в группе Библиотека функций.

Для того чтобы вставить в ячейку функцию СУММ, активизируйте ячейку, в которую необходимо ввести формулу, и выберите команду Формулы-Автосумма либо команду Главная-Редактирование-Сумма. В ячейке появится знак равенства и имя функции СУММ с подсказкой, в которой отображается список аргументов функции СУММ. Excel автоматически выделит один из диапазонов с числами, если текущая ячейка смежная с этим диапазоном, — вокруг выделенного диапазона возникнет движущаяся рамка, в текущей ячейке этот диапазон будет выделен. Если нужно указать другой диапазон, выделите его с помощью мыши. Вы увидите, что в формуле вместо исходной ссылки появилась ссылка на другой диапазон. Если необходимо задать несколько аргументов функции СУММ, при выделении несмежных диапазонов используйте клавишу <Ctrl>. При выделении следующего диапазона Excel автоматически вставит точку с запятой в список аргументов, а затем добавит новую ссылку.

Для вставки функции СУММ в формулу используйте комбинацию клавиш <Alt+=>.

Для того чтобы вставить в формулу другие функции — СРЗНАЧ, МИН, МАКС и СЧЁТ, — необходимо щелкнуть на маленькой кнопке с черным треугольником, расположенной рядом с кнопкой Автосумма или Сумма. Щелчок на этой кнопке открывает меню из шести команд.

· Сумма. При выборе этой команды Excel автоматически вставляет в текущую ячейку функцию СУММ, как было описано выше.

Вставка остальных функций выполняется аналогично.

· Среднее. Выполняется вставка функции СРЗНАЧ.

· Число. Выполняется вставка функции СЧЁТ.

· Максимум. Выполняется вставка функции МАКС.

· Минимум. Выполняется вставка функции МИН.

· Другие функции. Эта команда открывает диалоговое окно Мастер функций, в котором содержится список доступных функций

 

9. Обработка информации в электронных таблицах. Ссылки: относительные и абсолютные.

Если для различных исходных данных необходимо выполнять повторяющиеся вычисления по одинаковым формулам, то такие формулы можно копировать. При этом в формулах будут изменяться ссылки на ячейки с исходными данными. Например, если формулу =B2*C2 из ячейки D2 скопировать в ячейку D3, то в ячейке D3 она примет вид: =B3*C3.

При копировании формул в электронных таблицах применяется относительная адресация, при которой ссылки на ячейки в формуле изменяются в соответствии с новым положением скопированной формулы. Таким образом, при копировании формулы из одной ячейки в другую номер строки (обозначение столбца) изменяется на столько, на сколько строк (столбцов) сместилась формула.

Формулу из одной ячейки можно скопировать сразу в диапазон ячеек.

Для копирования формул в диапазон ячеек можно использовать автозаполнение. Для этого выделим ячейку с формулой и протащим маркер заполнения до ячейки D5. Формула будет скопирована во все ячейки диапазона D3:D5

Ссылки, которые изменяются при копировании формул, называют относительными. По умолчанию относительными являются все ссылки на ячейки в формулах. Механизм относительной адресации работает и при изменении количества строк и столбцов в электронной таблице.

Если в результате удаления (вставки) строк (столбцов) изменился адрес ячейки, на которую ссылается формула, то и ссылка тоже изменится так, чтобы выполнялись прежние вычисления.

Если необходимо, чтобы при копировании формул адреса ячеек не изменялись, используют абсолютные ссылки. Для создания абсолютной ссылки нужно поставить знак $ в формуле перед именем столбца и номером строки, например: $B$7. В смешанных ссылках при копировании формул остается неизменным только номер строки (например, B$7) или имя столбца ($B7).

Изменять тип ссылки в MS Excel удобно нажатием клавиши F4.

Сначала вводим в формулу адрес ячейки, например B7. По умолчанию он является относительной ссылкой. Затем устанавливаем на него указатель мыши. При нажатии клавиши F4 ссылка меняется на абсолютную: $B$7. Последующие два нажатия F4 дают смешанные ссылки: B$7 и $B7, затем снова появляется исходная относительная ссылка B7.

 

10. Обработка информации в электронных таблицах. Копирование и перемещение содержимого ячеек. Форматирование таблицы. Вставка и удаление строк и столбцов таблицы.