Городского округа города Шарья
Костромской области
Муниципальный методический конкурс
образовательных учреждений городского округа город Шарья
Костромской области,
2008-2009
Номинация:
«Методические разработки по теме,
модулю, разделу преподаваемого предмета»
Тема работы:
«Задачи на проценты.
Метод визуально-графической поддержки»
Автор:
Скворцова Светлана Александровна,
Учитель математики,
МОУ СОШ №2
2008-2009
І. Введение
Проценты – одно из математических понятий, которые часто встречаются в повседневной жизни. Так, мы часто читаем или слышим, что, например, в выборах приняли участие столько-то % избирателей, рейтинг победителя хит-парада равен стольки-то %, уровень инфляции составляет столько-то % в год, банк начисляет столько-то % годовых, молоко содержит столько-то % жира, материал содержит столько-то % хлопка и т.д.
Задачи на части и проценты часто вызывают затруднения у учащихся. Причина такой ситуации, на мой взгляд, в том, что тема «Проценты» изучается 5-ом классе, когда, собственно, математики ещё нет, изучается непродолжительно в конце учебного года, и, наконец, к изучению процентов не возвращаются в старших классах.
Решение задач используется для различных учебных целей: для формирования мотивации и интереса к учебной деятельности у учащихся, для иллюстрации и конкретизации изученного материала, выработки у учащихся специальных умений и навыков, для контроля и оценки результатов их учебной работы и т.д. Но есть ещё одна цель обучения математике, которая, к сожалению, меньше всего достигается в процессе обучения – формирование у учащихся общего подхода, общего метода, общего умения решать те или иные математические задачи.
Ведь, действительно, частные способы решения отдельных видов задач, изучаемых в школе, могут быть скоро забыты и в этом ничего страшного нет, а вот общие методы к решению задач должны сохраниться у каждого выпускника школы надолго, на всю жизнь.
Общий подход к решению задачи – это модель разумного подхода к решению любых бытовых, практических, технических задач, которые будут повседневно встречаться человеку. Ведь жить – это значит решать задачи.
І І. Основная часть.
По страницам учебника «МАТЕМАТИКА-6»
Ответ:3 кг.
Вторая часть задачи:
Чтобы получить данную схему, дети рассуждали так: берем 10 кг изюма, содержащего 55% воды. Добавляем х кг воды. В воде воды 100%.Получаем свежий виноград массой 10 + х кг, содержащий 90% воды.
Составляем уравнение:
90*(10+х)=55*10+100х
900+90х=550+100х
900-550=10х
350=1Ох
х=35
Ответ:45кг.
Рассмотрим № 592 учебника.
На столе лежал расколотый арбуз массой 10 кг, содержащий 99% воды. Через некоторое время часть воды испарилась и ее процентное содержание в арбузе понизилось до 96%.Найти новую массу арбуза.
Учащиеся рассуждают так: на столе лежал арбуз, массой 10кг, содержащий99% воды. Он раскололся. Испарилось х кг воды. В воде воды 100%. После этого арбуз стал весить 10- х кг и содержать 96% воды
В итоге рассуждений учащиеся 6 класса получают схему:
99*10-100х=96*(10-х)
990-100х=960-96х
30=4х
х=7,5
Ответ:2,5 кг.
Рассмотрим № 643 учебника.
Сколько получится муки из 15,2 тонн пшеницы, если масса муки составляет80 % массы зерна?
Рассуждаем так: при размоле зерна массой 15,2 т, содержащего 80% муки отбрасываем отходов х т содержащих 0% муки. Получаем 15,2- х т муки. В муке муки 100%.
 В результате такого рассуждения получили схему:
В результате такого рассуждения получили схему:
Составляем уравнение:
15,2*80-0*х=100(15,2-х)
1216=1520-100х
-304=-100х
х=3,04
Ответ: 12,16т
Задачи из материалов ЕГЭ
ЕГЭ 2003г. Уровень В-7
В баке находится 30 литров 30% раствора соли. Сколько воды надо добавить,
чтобы в растворе было 20% соли?
30*30=(х+30)*20
900=20х+600
20х=300
х=15
Ответ: 15 л.
ЕГЭ 2003г. Уровень В-7
Масса первого сплава на 3 кг больше массы второго сплава. Первый сплав Содержит 10% цинка, второй 40%.Новый сплав, полученный из двух первоначальных, содержит 20%цинка. Определить массу нового сплава.
10*(3+х)+40х=(3+2х)*20
30+10х+40х=60+40х
30+50х=60+40х
10х=30
х=3
Ответ:9кг
ЕГЭ 2003г. Уровень В-7
Свежие грибы содержат 92% воды, а сухие 8%.Сколько получится сухих
Грибов из 23 кг свежих?

23*92-100х=8(23-х)
2116-100х=184-8х
х=21
Ответ: 2кг.
ЕГЭ 2003г. Уровень В-7
 Влажность сухой цементной смеси на складе составляет 18%.Во время перевозки из-за дождей влажность повысилась на 2 %.Найти массу перевезенной смеси, если со склада было отправлено 400кг.
Влажность сухой цементной смеси на складе составляет 18%.Во время перевозки из-за дождей влажность повысилась на 2 %.Найти массу перевезенной смеси, если со склада было отправлено 400кг.
400*18+100х=(400+х)*20
7200+100х=8000+20х
800= -80х
х=10
Ответ:410 кг.
ЕГЭ 2003г. Уровень А
В одной смеси содержится 15 % вещества N, а во второй 30 %. Сколько нужно взять каждой смеси, чтобы получить 18 кг смеси с содержанием 20 % вещества N.

15х+540-30х=360
-15х= -180
х=12
Ответ: 12 кг, 6 кг.
ЕГЭ 2003г. Уровень - В
Имеется 2 раствора поваренной соли разной концентрации 40% и 60%. Эти
Растворов?

Составляем систему 2 уравнений:
ì40 х + 60 у + 5 * 0 = 20 (х + у + 5)
í
î40 х + 60 у + 400 = 70 (х + у + 5)
Ответ: х = 1; у = 2.
ЕГЭ 2003г. Уровень - В
 В двух сосудах содержится раствор кислоты в первом -70%, во втором - 46%. Из первого сосуда 1 л раствора перелили во второй и жидкость перемешали, затем из 2 сосуда 1л раствора перелили в 1 и также перемешали, после чего концентрация в 1 сосуде стала 68%.Сколько жидкости было во 2 сосуде, если в1 сосуде ее было 10л.
В двух сосудах содержится раствор кислоты в первом -70%, во втором - 46%. Из первого сосуда 1 л раствора перелили во второй и жидкость перемешали, затем из 2 сосуда 1л раствора перелили в 1 и также перемешали, после чего концентрация в 1 сосуде стала 68%.Сколько жидкости было во 2 сосуде, если в1 сосуде ее было 10л.
Аналогично решается система уравнений
Ответ: х = 5, у = 50
ЕГЭ 2003г. Уровень - В
Имеются 2слитка, представляющие собой сплавы цинка и меди. Масса 1 слитка 2 кг, 2-Зкг. Эти два слитка сплавили вместе с 5 кг сплава цинка и меди, в котором цинка было 45% и получили сплав, в котором цинка стало 50%, если бы процентное содержание цинка в 1 слитке было бы такое же как во 2, а во втором такое же как в 1, то сплавив эти 2 слитка с 5 кг сплава цинка с медью в котором 60% цинка получили бы сплав, в котором содержится 55% цинка. Найдите процентное содержание цинка в 1 и 2 слитках.
 Составляем систему уравнений:
Составляем систему уравнений:
ì2х + Зу + 225 = 500
í
î2у + 3х + 300 = 550
Ответ: 40%, 65%.
ЕГЭ-2005 г. Уровень С
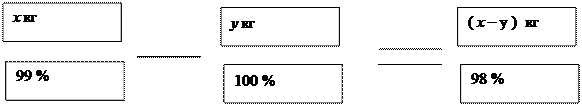 На овощной базе имелся крыжовник. Влажность, которого составляла 99%.3а время хранения его влажность уменьшилась на 1%. На сколько процентов уменьшилась масса хранившегося крыжовника?
На овощной базе имелся крыжовник. Влажность, которого составляла 99%.3а время хранения его влажность уменьшилась на 1%. На сколько процентов уменьшилась масса хранившегося крыжовника?
Составляем уравнение:
99 х – 100 у = 98 (х - у)
х = 2 у
(х - у) / х = (2у-у) / 2
у = у / 2
у =1 / 2
Ответ: масса уменьшилась вдвое, значит на 50%.
ЕГЭ-2005 г. В -7
 Имеются 2 слитка сплава серебра и олова. Первый слиток содержит 380г серебра и 40 г олова, а второй слиток 450 г серебра и 150 г олова. От каждого слитка взяли по куску, сплавили их и получили 200 г сплава, в котором оказался 81 % серебра. Определите массу в граммах куска, взятого от второго слитка.
Имеются 2 слитка сплава серебра и олова. Первый слиток содержит 380г серебра и 40 г олова, а второй слиток 450 г серебра и 150 г олова. От каждого слитка взяли по куску, сплавили их и получили 200 г сплава, в котором оказался 81 % серебра. Определите массу в граммах куска, взятого от второго слитка.
Составляем систему уравнений:
ì а + b = 200
ê а х + b х = 81 * 200
í
ï36 000 = 400 х
î 45 000 = 600 у
Ответ: 120 г.
ЕГЭ-2005 г. Уровень С
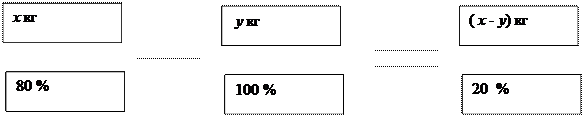 В свежих яблоках 80% воды, а в сушеных 20 %. На сколько % уменьшилась масса яблок при сушке?
В свежих яблоках 80% воды, а в сушеных 20 %. На сколько % уменьшилась масса яблок при сушке?
80 х – 100 у = 20 х – 20 у
60 х = 80 у
х = 80 у / 60 = 4 у / 3
Ответ:75%
ЕГЭ-2005 г. Уровень С
На 1 поле 65 % площади засеяно овсом, на 2 поле под овсом занято 45%площади. Известно, что на 1 и 2 полях вместе под овсом занято 53% общей площади. Какую часть всей площади составляет 1 поле?
Ответ: 40%.
ЕГЭ-2005 г. Уровень С
 Имеется два разных сплава меди со свинцом. Если взять 1 кг 1 сплава и 1 кг 2сплава и перемешать их, то получится сплав с содержанием 65% меди. Известно, что если взять кусок номер 1 первого сплава и кусок номер 2второго сплава, имеющих суммарную массу 7 кг и перемешать их, то получится сплав с содержанием меди 60%. Какова масса меди,содержащаяся в сплаве, если переплавить кусок 1 сплава равного по массе 2куска и 2 сплава равного по массе куску 1 сплава.
Имеется два разных сплава меди со свинцом. Если взять 1 кг 1 сплава и 1 кг 2сплава и перемешать их, то получится сплав с содержанием 65% меди. Известно, что если взять кусок номер 1 первого сплава и кусок номер 2второго сплава, имеющих суммарную массу 7 кг и перемешать их, то получится сплав с содержанием меди 60%. Какова масса меди,содержащаяся в сплаве, если переплавить кусок 1 сплава равного по массе 2куска и 2 сплава равного по массе куску 1 сплава.
Составляем систему уравнений:
ì х + у = 130
ï а х + b у = 420
í
ï b х + а у = 7 z
î а + b = 7
1) х + у = 130
b x + b y = 130 b
b x = 130 b – b y
2) x + y = 130
a x + a y = 130 a
a y = 130 a – a x
b x + a y = 130 b – b y + 130 a – a x = 130 (b+ a) – (a x + b y) = 130 * 7 – 420 = 490
7 * z = 490
z = 70
7* 0, 7 = 4,9 кг
Ответ: 4,9 кг.
Решение задач
1. Морская вода содержит 5 % по весу соли. Сколько кг пресной воды нужно прибавить к 40 кг морской воды, чтобы содержание соли в последней составляло 2 %?

40 * 5 + 0 * х = (40 + х) * 2
х = 60
Ответ:60кг.
- Имеется лом стали двух сортов с содержанием никеля 5% и40 %. Сколью
Ответ: 40 и 100т.
- Кусок сплава меди с оловом весом 12кг содержит 45% меди. Сколько чистого олова надо прибавить к этому куску, чтобы получившийся новый сплав имел 40 % меди?

12 * 45 + х * 0 = 40 (12 + х)
540 = 480 + 40 х
х = 1,5
Ответ: 441г.
- Древесина только что срубленного дерева содержит 64% воды. Через неделю количество воды стало 48% от веса дерева. Насколько уменьшился при этом вес дерева, если только что срубленное дерево весило 7,5 ц. Ответ округлить до десятых.

7,5 * 64 – 100 х = (7,5 – х) * 48
Ответ: приблизительно 2,3ц.
-
 Из 20 т руды выплавлено 8 т металла, содержащего 5% примеси. Каков процент примеси в руде?
Из 20 т руды выплавлено 8 т металла, содержащего 5% примеси. Каков процент примеси в руде?
10 * х – 1 200 = 40
20 х = 1 240
х = 6 2
Ответ: 62т.
- Если смешать 8 кг. и 2 кг. серной кислоты разной концентрации, то получится раствор 12% кислоты. При смешивании двух одинаковых масс тех же растворов получили 15% раствор. Определить первоначальную концентрацию растворов.

Составляем систему уравнений:
8 х + 2 у = 120
х + у = 30
Ответ: 10% и 20%.
-
 Сколько воды нужно выпарить из 0,5 т. целлюлозной массы, содержащей 85 % воды, чтобы получить массу с содержанием 75 % воды?
Сколько воды нужно выпарить из 0,5 т. целлюлозной массы, содержащей 85 % воды, чтобы получить массу с содержанием 75 % воды?
0,5 * 85 -100 х = 75 (0,5 – х)
х = 0.2 т.
Ответ: 0,2 т.
- Из руды, содержащей 25% примесей после переплавки получили 30 т металла. Сколько % примесей содержит, полученный металл?

38 * 25 – 8 * 100 = 30 х
Ответ: 5 %.
- Пчелы, перерабатывая цветочный нектар в мед освобождают его от значительной массы воды. Исследования показали, что нектар содержит 70 % воды, а полученный мед 17% воды. Сколько килограммов нектара приходится перерабатывать пчелам для получения 1 кг. меда?

70 х - (х – 1) * 100 = 1 7
70 х – 100 х + 100 = 17
- 30 х = - 93
х = 3
Ответ: приблизительно З кг.
- На складе есть 100кг. ягод. Проведенный анализ показал, что в ягодах содержится 99% воды. Через некоторое время анализ повторили. Оказалось что, содержание воды в ягодах упало до 98%. Какова теперь масса ягод?

99 * 100 – 100 х = 98 (100 – х)
9 900 – 100 х = 9 800 – 98 х
- 100 х + 98 х = 9 800 – 9 900
- 2 х = - 100
х = 50
Ответ: 50 кг ягод
- В банке находится 40 литров 40 % раствора сахарного песка. Сколько воды надо добавить, чтобы в растворе было 20 %песка?

40 * 40 = 20 (40 + х)
1 600 = 800 + 20 х
1 600 – 800 = 20 х
800 = 20 х
х = 40
Ответ: 40 л.
Ответ: 40 кг.
Следует обратить внимание учащихся,что ответ второго этапа решения задачи не является ответом на вопрос, поставленный в тексте задачи.
3. Тематическое планирование темы
| Класс
| Содержание
| Количество часов
| Результат обучения
|
|
| Задачи на выветривание, высыхание, испарение, процентное содержание.
|
| Иметь представление о визуально- графическом методе решения задач. Первичное применение и осмысление изученного.
|
|
| Задачи на процентное содержание и растворы.
|
| Применение визуально-графического метода. Уметь решать текстовые задачи на составление уравнений. Уметь отражать в письменной форме свои решения. Уметь рассуждать, выступать с решениями.
|
|
| Рациональные уравнения. Сплавы.(№98. 934,935)
|
| Составление и решение задач, выделяя три этапа математического моделирования. Формировать познавательные компетенции сравнения, сопоставления, классификации.
|
|
| Системы уравнений как математические модели реальных ситуаций.(196,197, 198.7.30; 7.49; 7.29;7.31)
|
| Знать, как составить математическую модель реальной ситуации и работать с составленной моделью. Уметь обосновывать суждения, правильно оформлять решения. выбрать из данной ситуации нужную. Уметь осмысливать ошибки и устранять их. Аргументировано отвечать на поставленные вопросы.
|
Поурочные разработки
Способ(арифметический)


1) 80 % = 0,80
2) 15,2 * 0,8 = 12,16 (т) – мука
Ответ: 12,16 т.
Способ (алгебраический)
Пусть х т мука, тогда (15,2 - х)- отходы, т.к. отходы это 20% составляем уравнение:
(15,2 – х): 0,2 = 15,2
15,2 – х = 15,2 * 0,2
15,2 – х = 3,04
х = 15,2 - 3,04
х = 12,16
Ответ: 12,16 т.
Ознакомление с новым материалом:
Параллельно с работой над текстом задачи на доске изображается рисунок-схема:

Составляем уравнение:
15,2 * 80 = 100 х
1 216 = 100 х
Х = 12,16
Ответ 12,16 т.
Вывод: (ученики делают самостоятельно). Сравнивают способы решения задач
.



- Первичное осмысление и применение изученного. Индивидуальная работа с раздаточным материалом.
I I I.Заключение
Покажем превосходство визуально-графического метода по сравнению с алгебраическим на примере конкурсной задачи.
Задача. В 500 кг руды содержится некоторое количество железа. После удаления из руды 200 кг примесей, содержащих в среднем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20%. Определите, какое количество железа осталось ещё в руде?
Алгебраический способ решения:
|
| Масса руды, в кг
| Масса железа, в кг
| Концентрация (доля железа в руде)
|
| Руда
|
| х кг
| х /500
|
| Руда после удаления примесей
| 500-200=300
| х – 0,12 * 200= х - 25
| х – 25 / 300
|
1) 500 – 200 = 300 (кг) – масса руды после удаления примесей.
2) 0,125 * 200 = 25 (кг) – масса железа в 200 кг примесей.
Пусть
х кг - масса железа в руде,
(х – 25) кг – масса железа в руде после удаления примесей.
х / 500 – доля железа в руде,
х - 25 / 300 – доля железа в руде после удаления примесей.
По условию, содержание железа в оставшейся руде повысилось на 20% = 0,2.
Составим уравнение:
| 5 (х -25)
|
|
|
| 3 х
|
|
|
| 1 500
|
| 1 500
| 1 500
|
5 х – 125-300-3 х = 0,
2 х = 425,
х = 212,5.
212,5 кг – масса железа в руде.
3) 212,5 – 25 = 187,5 (кг) – железа осталось в руде после удаления примесей.
Ответ: 187,5 кг.
Метод визуально-графической поддержки:
Руда 500 кг
500 х – 200 * 12.5 = 300 (х + 20)
500 х – 2 500 = 300 х + 6000
200 х = 8 500
х = 42,5
42,5 + 20 = 62,5 % - содержание железа в оставшейся руде.
62,5 х 300 = 187,5 (кг) – осталось железа в руде после удаления примесей.
Ответ: 187,5 кг.
Итак, сравним первый этап решения задачи: перевода условия задачи с математического языка на обычный. При визуально-графическом методе словесно это звучит так: из 500кг руды удалили 200 кг примесей, получили 300 кг оставшейся руды. Руда содержит х % железа, примеси 12,5% железа, а оставшаяся руда (х +20) % железа Входе перевода задачи появляется схема. И этого достаточно, чтобы получилась математическая модель. А при алгебраическом методе требуется умение находить дробь от числа, затем долю железа в руде до и после удаления примесей, а это вызывает затруднения у школьников. Далее получается дробное уравнение. А оно сложнее линейного.
Первый этап при визуально графическом методе решения текстовых задач проще, короче. нагляднее. Для изучения математики большое значение имеет зрительная память.
Далее. преимущество этого метода- он охватывает широкий спектр задач: на концентрацию. процентное содержание, сплавы. выветривание. усыхание т. е. все.кроме «банковских».
Этот метод можно применять и в смежных дисциплинах: химии, физике. Биологии. Географии. Самостоятельный перенос приемов деятельности в новые ситуации- это черта творческой деятельности учащегося. И все это позволяет выполнить метод визуально-графической поддержки.
IV.Приложение
Задачи для самостоятельного решения
Задача 1
В 500 кг руды содержится некоторое количество железа. После удаления из руды 200кг примесей, содержащих в среднем 12.5% железа. Содержание железа в оставшейся руде повысилось на 20%.Определите, какое количество железа осталось еще в руде?
Ответ: 187.5 кг.
Задача 2.
Сколько воды нужно вы парить из 40 кг 20% раствора соли, чтобы получить 25% раствор этой соли?
Ответ: 8кг.
Задача 3.
Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?
Ответ: 70 кг.
Задача 4.
Смешали 30% раствор соляной кислоты с 10% и получили 600 г 15 % раствора. Сколько граммов каждого раствора было взято?
Ответ: 150 г и 450 г.
Задача 5
Кусок сплава массой 36 кг содержит 45 % меди. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60 % меди?
Ответ: 13,5кг.
Задача 6.
Имеется два сплава меди с разным содержанием меди. Число,выражающее в процентах содержание меди в первом сплаве, на 40 меньше числа, выражающего в процентах содержание меди во втором сплаве. Оба эти сплава сплавили вместе, после чего содержание меди составило 36 процентов. Определить процентное содержание меди в первом и во втором сплавах, если известно, что в первом сплаве меди было 6 кг, а во втором -12кг.
Ответ: 20% и 60%.
Задача 7.
Имеется кусок сплава меди с оловом общей массой 12 кг, содержащей 45% меди. Сколько чистого олова надо прибавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди?
Ответ: 1,5 кг
Задача 8.
В бидон налили 3 литра молока 1% жирности и 7 литров молока 6 % жирности. Какова жирность, полученного молока?
Ответ: 4,5 %.
Задача 9.
Торговец продает орехи двух сортов одни по 90 центов другие по 60 центов за кг. Он хочет получить 50 кг смеси по 72 цента за кг. Сколько для этого потребуется орехов каждого сорта?
Ответ: 20 кг и 30 кг.
Задача 10.
Сколько граммов воды можно выпарить из 80г 6 % раствора соли. Чтобы получить раствор содержащий 10 % соли?
Ответ: 32 г.
Задача 11.
Имеется два кислотных раствора: один 20 %., другой 30 %. Взяли 0.5 л первого и 1,5 л второго и образовали новый раствор. Какова концентрация кислоты в новом растворе?
Ответ: 27.5 %
Задача 12.
Смешали 300 г 50 % и 100 г 30 % раствора кислоты. Определите процентное содержание кислоты в полученной смеси.
Ответ:45 %.
Задача 13.
Сколько чистой воды надо добавить к 300 г морской воды. Содержащей 4 5 соли. Чтобы получить воду, содержащую 3 5 соли?
Задача 14.
Имеется два сосуда. содержащие 4 кг и 6 кг раствора кислоты различной концентрации. Если их слить вместе. То получим раствор, содержащий 35% кислоты. Если же слить равные массы этих растворов. То получим раствор, содержащий 36% кислоты. Сколько кг кислоты содержится в каждом растворе?
Ответ: 1.64 кг и 1.86 кг
Задача 15.
Имеются две смеси апельсинового и ананасового соков. Первая смесь содержит 40 % апельсинового сока, а вторая 80%. Смешиваются х л первой смеси и у л второй, в результате получается 20 л смеси, содержащей 70 % апельсинового сока. Определите х и у.
Ответ: х = 5 у = 15 л.
городского округа города Шарья
Костромской области








 В результате такого рассуждения получили схему:
В результате такого рассуждения получили схему:



 Влажность сухой цементной смеси на складе составляет 18%.Во время перевозки из-за дождей влажность повысилась на 2 %.Найти массу перевезенной смеси, если со склада было отправлено 400кг.
Влажность сухой цементной смеси на складе составляет 18%.Во время перевозки из-за дождей влажность повысилась на 2 %.Найти массу перевезенной смеси, если со склада было отправлено 400кг.

 В двух сосудах содержится раствор кислоты в первом -70%, во втором - 46%. Из первого сосуда 1 л раствора перелили во второй и жидкость перемешали, затем из 2 сосуда 1л раствора перелили в 1 и также перемешали, после чего концентрация в 1 сосуде стала 68%.Сколько жидкости было во 2 сосуде, если в1 сосуде ее было 10л.
В двух сосудах содержится раствор кислоты в первом -70%, во втором - 46%. Из первого сосуда 1 л раствора перелили во второй и жидкость перемешали, затем из 2 сосуда 1л раствора перелили в 1 и также перемешали, после чего концентрация в 1 сосуде стала 68%.Сколько жидкости было во 2 сосуде, если в1 сосуде ее было 10л. Составляем систему уравнений:
Составляем систему уравнений: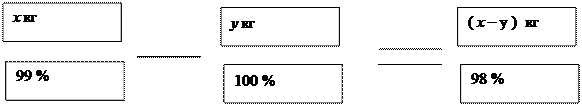 На овощной базе имелся крыжовник. Влажность, которого составляла 99%.3а время хранения его влажность уменьшилась на 1%. На сколько процентов уменьшилась масса хранившегося крыжовника?
На овощной базе имелся крыжовник. Влажность, которого составляла 99%.3а время хранения его влажность уменьшилась на 1%. На сколько процентов уменьшилась масса хранившегося крыжовника? Имеются 2 слитка сплава серебра и олова. Первый слиток содержит 380г серебра и 40 г олова, а второй слиток 450 г серебра и 150 г олова. От каждого слитка взяли по куску, сплавили их и получили 200 г сплава, в котором оказался 81 % серебра. Определите массу в граммах куска, взятого от второго слитка.
Имеются 2 слитка сплава серебра и олова. Первый слиток содержит 380г серебра и 40 г олова, а второй слиток 450 г серебра и 150 г олова. От каждого слитка взяли по куску, сплавили их и получили 200 г сплава, в котором оказался 81 % серебра. Определите массу в граммах куска, взятого от второго слитка.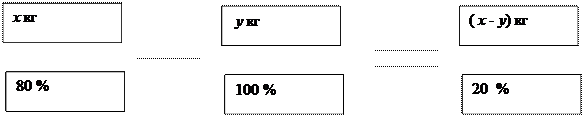 В свежих яблоках 80% воды, а в сушеных 20 %. На сколько % уменьшилась масса яблок при сушке?
В свежих яблоках 80% воды, а в сушеных 20 %. На сколько % уменьшилась масса яблок при сушке? Имеется два разных сплава меди со свинцом. Если взять 1 кг 1 сплава и 1 кг 2сплава и перемешать их, то получится сплав с содержанием 65% меди. Известно, что если взять кусок номер 1 первого сплава и кусок номер 2второго сплава, имеющих суммарную массу 7 кг и перемешать их, то получится сплав с содержанием меди 60%. Какова масса меди,содержащаяся в сплаве, если переплавить кусок 1 сплава равного по массе 2куска и 2 сплава равного по массе куску 1 сплава.
Имеется два разных сплава меди со свинцом. Если взять 1 кг 1 сплава и 1 кг 2сплава и перемешать их, то получится сплав с содержанием 65% меди. Известно, что если взять кусок номер 1 первого сплава и кусок номер 2второго сплава, имеющих суммарную массу 7 кг и перемешать их, то получится сплав с содержанием меди 60%. Какова масса меди,содержащаяся в сплаве, если переплавить кусок 1 сплава равного по массе 2куска и 2 сплава равного по массе куску 1 сплава.


 Из 20 т руды выплавлено 8 т металла, содержащего 5% примеси. Каков процент примеси в руде?
Из 20 т руды выплавлено 8 т металла, содержащего 5% примеси. Каков процент примеси в руде? 
 Сколько воды нужно выпарить из 0,5 т. целлюлозной массы, содержащей 85 % воды, чтобы получить массу с содержанием 75 % воды?
Сколько воды нужно выпарить из 0,5 т. целлюлозной массы, содержащей 85 % воды, чтобы получить массу с содержанием 75 % воды? 












