Рекомендуемая учебная литература: [ 1 ], часть 1: гл..VII- IX, § 63-76, с.143–176; [ 2 ]: гл. IX, § 36–46, с.95–116.
Задача К1 – на определение скорости и ускорения точки no заданным в координатной форме уравнениям ее движения.
По определению скорость точки 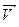 в данный момент времени – это вектор, равный производной от радиуса-вектора движущейся точки по времени и направленный по касательной к траектории точки в сторону движения
в данный момент времени – это вектор, равный производной от радиуса-вектора движущейся точки по времени и направленный по касательной к траектории точки в сторону движения
 . (2.1)
. (2.1)
В декартовой системе координат Охуz, принимаемой за неподвижную, радиус-вектор движущейся точки (рис. 13) определяется равенством:
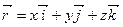 ,
,
где  – орты координатных осей;
– орты координатных осей;
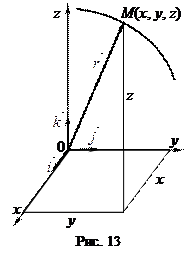 x = x (t), y = y (t), z = z (t). (2.2)
x = x (t), y = y (t), z = z (t). (2.2)
Уравнения (2.2) являются уравнениями движения точки, заданные координатным способом. Эти же уравнения являются уравнениями траектории точки (рис. 13) в параметрическом виде, где параметром является время t. Для определения траектории точки в случае задания ее движения координатным способом необходимо из уравнения (2.2) исключить время t. Для определения скорости точки, заданной координатным способом, по формуле (2.1) имеем
 =
=  , (2.3)
, (2.3)
где  – проекции вектора скорости точки на неподвижные декартовы координаты.
– проекции вектора скорости точки на неподвижные декартовы координаты.
Модуль скорости определяется формулой
 . (2.4)
. (2.4)
Направление вектора скорости определяется направляющими косинусами:
 .
.
Ускорение точки определяется как первая производная от вектора скорости по времени:
 =
= 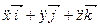 , (2.5)
, (2.5)
где  – проекции вектора ускорения точки на неподвижные декартовы координаты.
– проекции вектора ускорения точки на неподвижные декартовы координаты.
Модуль вектора ускорения вычисляется аналогично модулю вектора скорости:
 , (2.6)
, (2.6)
а направление вектора ускорения – направляющими косинусами:
 .
.
Движение точки может быть задано также естественным способом. При этом способе должна быть известна траектория точки и задан закон движения точки М по этой траектории: s = s (t), где  – дуга, отсчитываемая на траектории от начального положения точки M 0.
– дуга, отсчитываемая на траектории от начального положения точки M 0.
 Для определения положения точки на траектории задается также направление положительного отсчета дуги (рис. 14).
Для определения положения точки на траектории задается также направление положительного отсчета дуги (рис. 14).
Рис. 14 Рис. 15
При этом способе используются естественные оси с началом в текущем положении точки М на траектории (рис. 15) и единичными векторами  . Единичный вектор
. Единичный вектор  направлен по касательной к траектории в сторону положительного отсчета дуги, единичный вектор
направлен по касательной к траектории в сторону положительного отсчета дуги, единичный вектор  направлен по главной нормали траектории в сторону се вогнутости, единичный вектор
направлен по главной нормали траектории в сторону се вогнутости, единичный вектор  направлен по бинормали траектории в точке М.
направлен по бинормали траектории в точке М.
Орты  и
и  лежат в соприкасающейся плоскости, орты
лежат в соприкасающейся плоскости, орты  и
и  в нормальной плоскости, орты
в нормальной плоскости, орты  и
и  – в спрямляющей плоскости.
– в спрямляющей плоскости.
Скорость точки при естественном способе задания движения точки определяется формулой
 ,
,
где проекция вектора скорости на касательную  определяется по формуле:
определяется по формуле:
 . (2.7)
. (2.7)
Модуль вектора скорости  .
.
Вектор ускорения точки лежит в соприкасающейся плоскости и раскладывается на касательную и нормальную составляющие:
 ,
,
где проекция вектора ускорения на касательную
 (2.8)
(2.8)
называется касательным (тангенциальным) ускорением.
Касательное ускорение характеризует «быстроту» изменения величины скорости. При  (векторы касательного ускорения и скорости направлены в одну сторону) точка в данный момент времени движется ускоренно, при
(векторы касательного ускорения и скорости направлены в одну сторону) точка в данный момент времени движется ускоренно, при 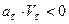 (векторы касательного ускорения и скорости направлены в разные стороны) – замедленно.
(векторы касательного ускорения и скорости направлены в разные стороны) – замедленно.
Проекция ускорения на главную нормаль
 , (2.9)
, (2.9)
где r – радиус кривизны траектории в точке М, называется нормальным ускорением.
Модуль вектора ускорения определяется по формуле
 . (2.10)
. (2.10)
Направление вектора ускорения определяется направляющими косинусами
 .
.
В соответствии с вышеизложенным задачу К1 необходимо решать в следующей последовательности:
1) выбрать систему координат;
2) исключив время из уравнений движения точки, определить уравнение траектории точки и изобразить ее график;
3) определить на графике положение точки в заданный момент времени;
4) по заданным уравнениям движения точки определить проекции скорости точки и модуль скорости по формулам (2.3) и (2.4) соответственно;
5) построить на рисунке вектор скорости точки в заданный момент времени;
6) по формулам (2.5) и (2.6) определить ускорение точки;
7) построить на рисунке вектор ускорения точки в заданный момент времени;
8) взять производную по времени от модуля скорости и составить выражение для квадрата касательного ускорения;
9) используя формулу (2.10), вычислить нормальное ускорение;
10) используя формулу нормального ускорения (2.9), вычислить радиус кривизны траектории в заданный момент времени;
11) разложить ускорение точки на касательную и нормальную составляющие на рисунке;
12) определить по касательному ускорению характер движения точки в заданный момент времени.
Пример выполнения задания
Движение точки М в плоскости х,у задано уравнениями
 (х, у – в см, t – в с) (2.11)
(х, у – в см, t – в с) (2.11)
Определить траекторию точки и для момента времени t 1 = 1/2 с найти положение точки M на траектории, ее скорость, полное, касательное и нормальное ускорения. Определить также радиус кривизны траектории в точке М.
Решение. Определим траекторию точки М, исключив из уравнений движения (2.11) время t. С этой целью преобразуем уравнения (2.11), приведя тригонометрические функции к одному аргументу:
 . (2.12)
. (2.12)
Подставляя (2.12) и первое уравнение (2.11), получим 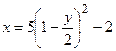 или
или  .
.
Траекторией точки является парабола (рис. 16).
Определим начальное положение точки М 0: при t = 0 x 0 = 5 cos2 0 – 2 = 3, у 0 = 4 sin2 0 = 0.
В момент времени t 1 = 1/2 с точка M имеет координаты:
 .
.
Определим проекции скорости точки по формулам (2.3):
 ,
,

 . (2.13)
. (2.13)
Рис. 16
По формуле (2.4) определим модуль скорости:

 . (2.14)
. (2.14)
Определим проекции и модуль скорости в момент времени t 1 = 1/2 с:

Вектор скорости строим (рис. 16) по составляющим:
 .
.
Определим проекции ускорения точки М, вычисляя производные по времени от проекций се скорости (2.13):

По формуле (2.6) определим модуль ускорения:
 .
.
При t 1 = 1/2 с  ,
, 
 , следовательно, a 1 = 3,48 см/с2, и вектор ускорения
, следовательно, a 1 = 3,48 см/с2, и вектор ускорения  направлен вертикально вверх.
направлен вертикально вверх.
Найдем производную от функции скорости (2.14) по времени:

При t 1 = 1/2 с  .
.
Учитывая, что  , вычислим нормальное ускорение по формуле (2.10):
, вычислим нормальное ускорение по формуле (2.10):
 .
.
Радиус кривизны вычислим по формуле (2.9)
 .
.
Поскольку векторы скорости и касательного ускорения направлены в одну сторону, точка в данный момент времени движется ускоренно.





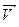 в данный момент времени – это вектор, равный производной от радиуса-вектора движущейся точки по времени и направленный по касательной к траектории точки в сторону движения
в данный момент времени – это вектор, равный производной от радиуса-вектора движущейся точки по времени и направленный по касательной к траектории точки в сторону движения . (2.1)
. (2.1)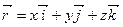 ,
, – орты координатных осей;
– орты координатных осей; x = x (t), y = y (t), z = z (t). (2.2)
x = x (t), y = y (t), z = z (t). (2.2) =
=  , (2.3)
, (2.3) – проекции вектора скорости точки на неподвижные декартовы координаты.
– проекции вектора скорости точки на неподвижные декартовы координаты. . (2.4)
. (2.4) .
. =
= 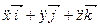 , (2.5)
, (2.5) – проекции вектора ускорения точки на неподвижные декартовы координаты.
– проекции вектора ускорения точки на неподвижные декартовы координаты. , (2.6)
, (2.6) .
. – дуга, отсчитываемая на траектории от начального положения точки M 0.
– дуга, отсчитываемая на траектории от начального положения точки M 0. Для определения положения точки на траектории задается также направление положительного отсчета дуги (рис. 14).
Для определения положения точки на траектории задается также направление положительного отсчета дуги (рис. 14). . Единичный вектор
. Единичный вектор  направлен по касательной к траектории в сторону положительного отсчета дуги, единичный вектор
направлен по касательной к траектории в сторону положительного отсчета дуги, единичный вектор  направлен по главной нормали траектории в сторону се вогнутости, единичный вектор
направлен по главной нормали траектории в сторону се вогнутости, единичный вектор  направлен по бинормали траектории в точке М.
направлен по бинормали траектории в точке М. ,
, определяется по формуле:
определяется по формуле: . (2.7)
. (2.7) .
. ,
, (2.8)
(2.8) (векторы касательного ускорения и скорости направлены в одну сторону) точка в данный момент времени движется ускоренно, при
(векторы касательного ускорения и скорости направлены в одну сторону) точка в данный момент времени движется ускоренно, при 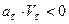 (векторы касательного ускорения и скорости направлены в разные стороны) – замедленно.
(векторы касательного ускорения и скорости направлены в разные стороны) – замедленно. , (2.9)
, (2.9) . (2.10)
. (2.10) .
. (х, у – в см, t – в с) (2.11)
(х, у – в см, t – в с) (2.11) . (2.12)
. (2.12)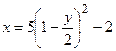 или
или  .
. .
. ,
,
 . (2.13)
. (2.13)
 . (2.14)
. (2.14)
 .
.
 .
. ,
, 
 , следовательно, a 1 = 3,48 см/с2, и вектор ускорения
, следовательно, a 1 = 3,48 см/с2, и вектор ускорения  направлен вертикально вверх.
направлен вертикально вверх.
 .
. , вычислим нормальное ускорение по формуле (2.10):
, вычислим нормальное ускорение по формуле (2.10): .
. .
.


