LR
ГРАФИКПАРАМЕТРЫ
Эталон: 1___,___; 2___,___; 3___,___; 4___,___.
| Инструкция для студентов.В задании указать правильную последовательность упорядочиваемых элементов в специальной строке ответа-эталона.
|
УСТАНОВИТЕ ПРАВИЛЬНУЮ ПОСЛЕДОВАТЕЛЬНОСТЬ
31. ПОСЛЕДОВАТЕЛЬНОСТЬОПРЕДЕЛЕНИЯ СЛУЧАЙНОГО СОБЫТИЯ. СЛУЧАЙНОЕ СОБЫТИЕ - .....
1 – нельзя
2 - оно может произойти
3 - это событие,
4 - или не произойти
5 - наступление которого
6 - достоверно предвидеть;
7 - в одних и тех же условиях
Эталон: _, _, _, _, _, _, _.
32. ПОСЛЕДОВАТЕЛЬНОСТЬ ФОРМУЛИРОВКИ ЗАКОНА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ ДЛЯ ДВУХ НЕСОВМЕСТНЫХ СОБЫТИЙ
1 - из двух несовместных событий
2 - одного
3 - их вероятностей
4 - (безразлично какого)
5 – события
6 - вероятность появления
7 - равна сумме Эталон: _, _, _, _, _, _, _.
33.ПОСЛЕДОВАТЕЛЬНОСТЬОПРЕДЕЛЕНИЯ РАВНОВОЗМОЖНЫХ СОБЫТИЙ. РАВНОВОЗМОЖНЫЕ СОБЫТИЯ…...
1 - из-за которых
2 - если при испытаниях
3 – происходит
4 - имеют место
5 - одно событие
6 - нет каких - либо причин
7 - чаще другого
Эталон:_, _, _, _, _, _, _.
| Инструкция для студентов. При выполнении заданий следует записать ответ, состоящий из трех пунктов. Схема ответа: • Высказывание А: верно/неверно; • Высказывание В: верно/неверно; • Связь : есть/нет.
|
УСТАНОВИТЕ ПРИЧИННО - СЛЕДСТВЕННУЮ СВЯЗЬ
34. А. ДИСПЕРСИЯ И СРЕДНЕЕ КВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ИМЕЮТ ОДИНАКОВЫЕ ЕДИНИЦЫ ИЗМЕРЕНИЯ.
ПОТОМУ ЧТО
Б. ДИСПЕРСИЯ И СРЕДНЕЕ КВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ХАРАКТЕРИЗУЮТ РАССЕЯНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ОКОЛО МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ.
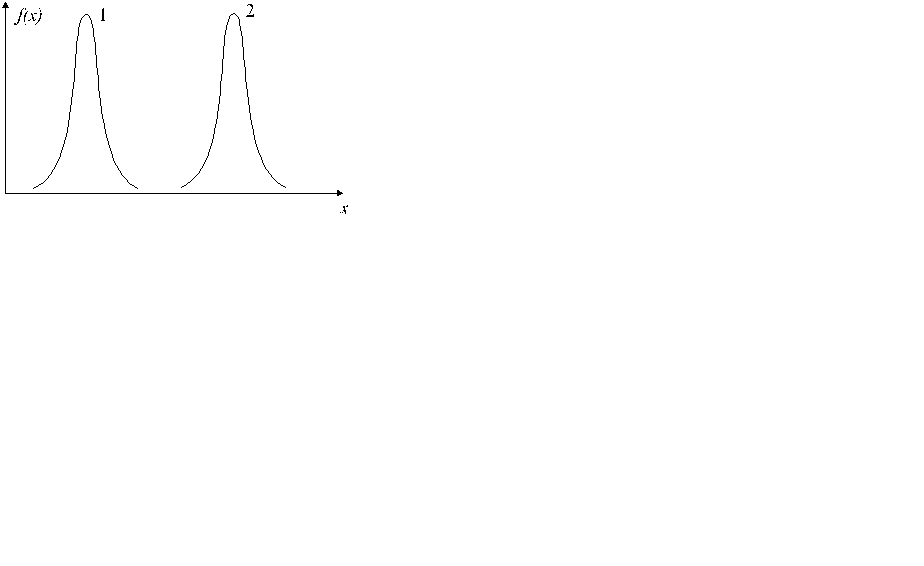
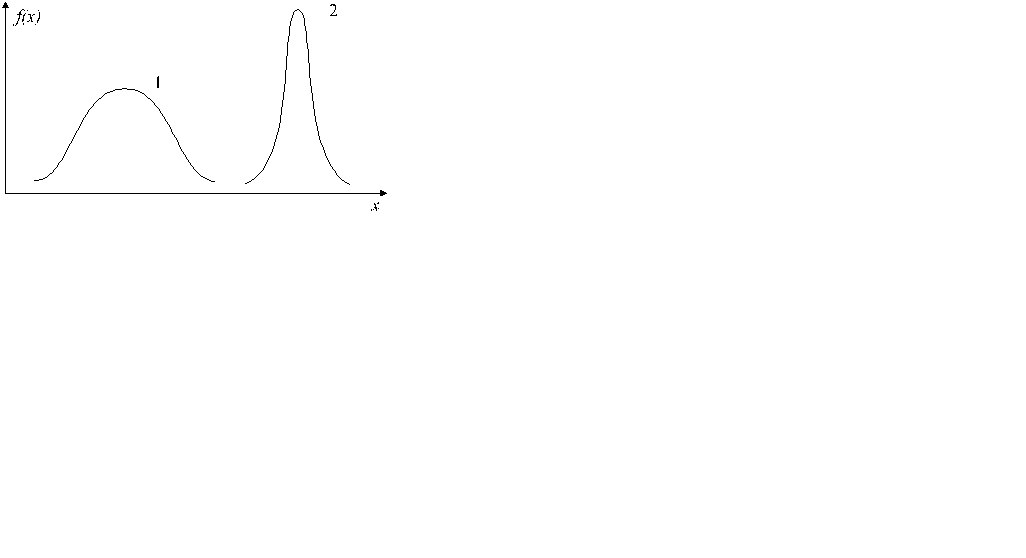
35. А. ИЗМЕНЕНИЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ПРИ ПОСТОЯННОМ СРЕДНЕМ КВАДРАТИЧНОМ ОТКЛОНЕНИИ НЕ МЕНЯЕТ ФОРМУ КРИВОЙ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ.
ПОТОМУ ЧТО
Б. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ХАРАКТЕРИЗУЕТ ПОЛОЖЕНИЕ КРИВОЙ НА ОСИ АБСЦИСС.
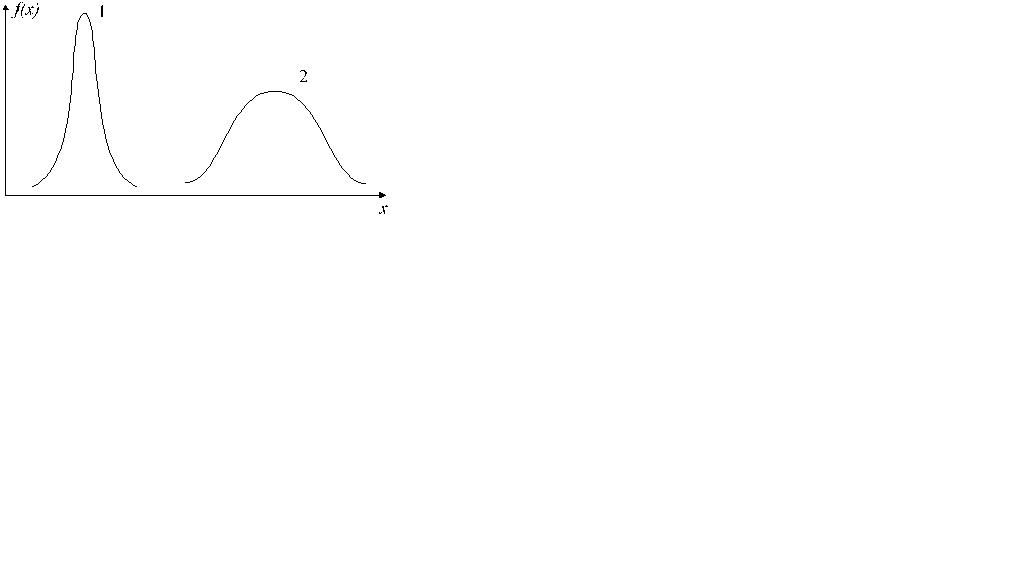
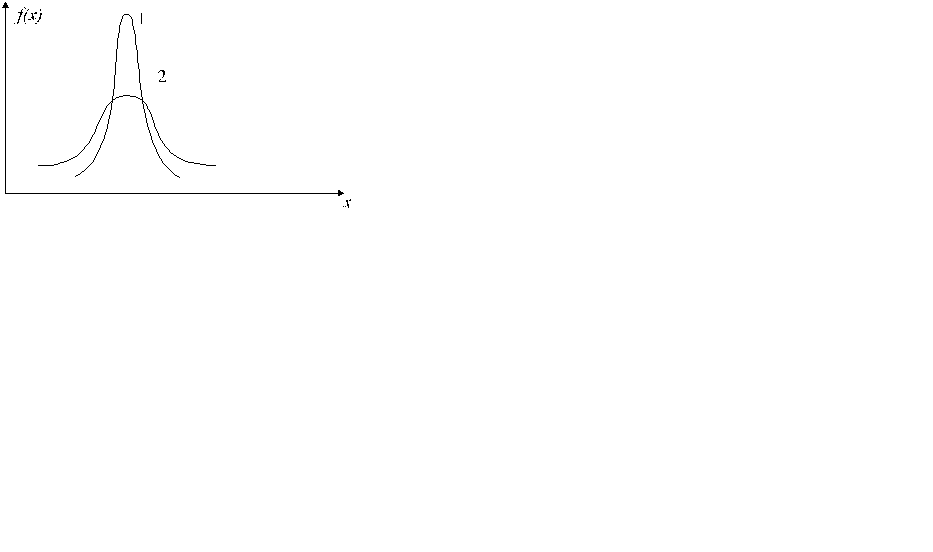
36.ПРИ УВЕЛИЧЕНИИ СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ КРИВАЯ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ СТАНОВИТСЯ БОЛЕЕ ОСТРОВЕРШИННОЙ
ПОТОМУ ЧТО
Б.СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ ХАРАКТЕРИЗУЕТ ПОЛУШИРИНУ КРИВОЙ.
37. А. ИЗМЕНЕНИЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ПРИ ПОСТОЯННОМ СРЕДНЕМ КВАДРАТИЧЕСКОМ ОТКЛОНЕНИИ НЕ МЕНЯЕТ ФОРМУ КРИВОЙ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ.
ПОТОМУ ЧТО
Б. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ХАРАКТЕРИЗУЕТ ПОЛОЖЕНИЕ КРИВОЙ НА ОСИ АБСЦИСС.
| Инструкция для студентов. При выполнении заданий следует записать решение с полным его обоснованием.
|
РЕШИТЕ ЗАДАЧИ
1. Брошены две монеты и игральная кость. Вероятность совмещения событий: «появился орел» , «появился орел», «появилось нечетное число очков»равна…….
2. Из колоды в 36 карт наудачу вынимается одна. Вероятность того, что будет вынута пика или туз равна……
3.Среди 1000 лотерейных билетов имеется 100выигрышных. Вероятность того, что три, один за другим выбранных билета, будут выигрышными, равна……..
4. Вероятность рождения мальчика равна 0,515.
· Вероятность того, что в семьях из двух детей первый ребенок - мальчик, второй – девочка равна………
· Вероятность того, что в семьях из двух детейодин из детей - мальчик, другой – девочка равна……
5. В аптечке находится 10 белых и 5розовых таблеток. Из аптечки дважды берут наудачу по одной таблетке, не возвращая их назад. Вероятность появления белой таблетки во второмслучае, если сначала достали розовую таблетку, равна…….
6. В большой популяции плодовой мушки 25% мух имеют мутацию глаз, 50% - мутацию крыльев, а 40% мух с мутацией глаз имеют и мутацию крыльев. Вероятность того, что у мухи наудачу выбранной из этой популяции, окажется хотя бы одна из этих мутаций, равна…….
7.Пусть вероятность того, что забег выиграет первый студент равна 1/3, а вероятность того, что забег выиграет второй студент равна 1/5. Вероятность того, что забег выиграет один из них, равна……..
8.Один стрелок поражает цель с вероятностью 0,85, а другой поражает цель с вероятностью 0,7. Стреляют одновременно. Вероятность поражения цели при попадании в нее хотя бы одной из двух пуль равна………..
9.Медсестра обслуживает трех пациентов. Вероятность того, что в течение часа пациент потребует внимания медсестры, равна для первого пациента – 0,2, для второго – 0, 5, для третьего – 0,7. Вероятность того, что по крайней мере один из пациентов не потребует внимания медсестры в течение часа, равна…...
10. В урне находятся 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну.
Вероятность того, что при первом испытании появится белый шар, при втором - черный и при третьем – синий равна…….
11.В ящике находится 130 шаров: 18 красных, 50 синих, 42 желтых и 20 белых. Вероятность того, что вынутые один за другим два шара будут цветными, равна……...
12.На медицинском предприятии 95% изготовленных деталей признаются годными. При этом из каждой сотни годных деталей 70% оказываются первого сорта. Вероятность того, что изделие, изготовленное на этом предприятии, будет первого сорта, равна………..
13.За определенный срок наблюдения зарегистрировали 14 солнечных и несколько пасмурных дней. Вероятность солнечного дня составила 0,7. Пасмурных дней было……
14.Бросают два игральных кубика. Вероятность того, что на первом кубике выпадет четное число очков, а на втором – число меньше 6 равна…….
15.Дана дифференциальная функция случайной величины
Xf(x) = 2x, при 0<x£ 1. Вероятность того, что в результате испытания X примет значения, принадлежащие интервалу 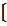 0,5; 1 ]равна…...
0,5; 1 ]равна…...
16. 80 пробирок находятся в ящике. Из них 4 имеют трещины. Вероятность того, что вынутые одна за другой две пробирки окажутся с трещинами равна….
17 .Дискретная случайная величина задана законом распределения
| Xi
| 7
| 8
| 9
| 10
|
| Pi
| 0,2
| 0,15
| 0,1
| 0,55
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
18. Дискретная случайная величина задана законом распределения
| Xi
| 2
| 3
| 4
| 5
|
| Pi
| 0,25
| 0,15
| 0,5
| 0,1
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
19. Дискретная случайная величина задана законом распределения
| Xi
| 28
| 30
| 40
| 45
|
| Pi
| 0,3
| 0,1
| 0,5
| 0,1
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
20. Дискретная случайная величина задана законом распределения
| Xi
| 21
| 22
| 24
| 25
|
| Pi
| 0,2
| 0,1
| 0,2
| 0,5
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
21. Дискретная случайная величина задана законом распределения
| Xi
| 8
| 9
| 10
| 11
|
| Pi
| 0,2
| 0,2
| 0,2
| 0,4
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
22. Дискретная случайная величина задана законом распределения
| Xi
| 10
| 13
| 14
| 15
|
| Pi
| 0, 2
| 0, 15
| 0, 1
| 0,55
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
23.Дискретная случайная величина задана законом распределения
| Xi
| 2
| 3
| 4
| 5
|
| Pi
| 0,1
| 0,1
| 0,2
| 0,6
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
24.Дискретная случайная величина задана законом распределения
| Xi
| 3
| 4
| 5
| 7
|
| Pi
| 0,5
| 0,1
| 0,3
| 0,1
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
25. Дискретная случайная величина задана законом распределения
| Xi
| 20
| 30
| 40
| 50
|
| Pi
| 0,2
| 0,15
| 0,1
| 0,55
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
26. Дискретная случайная величина задана законом распределения
| Xi
| 3
| 5
| 6
| 7
|
| Pi
| 0,2
| 0,1
| 0,1
| 0,6
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
27. Дискретная случайная величина задана законом распределения
| Xi
| 2
| 3
| 4
| 7
|
| Pi
| 0,3
| 0,1
| 0,1
| 0,5
|
| | | | | |
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
28. Дискретная случайная величина задана законом распределения
| Xi
| 2
| 3
| 4
| 5
|
| Pi
| 0,2
| 0,15
| 0,1
| 0,55
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
29. Дискретная случайная величина задана законом распределения
| Xi
| 1
| 2
| 3
| 4
| 5
| 6
|
| Pi
| 0,22
| 0,15
| 0,16
| 0,18
| 0,15
| 0,14
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
30.Дискретная случайная величина задана законом распределения
| Xi
| 10
| 13
| 14
| 15
|
| Pi
| 0,4
| 0,1
| 0,2
| 0,3
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
31. Дискретная случайная величина задана законом распределения
| Xi
| 3
| 4
| 5
| 7
| 9
|
| Pi
| 0,35
| 0,1
| 0,4
| 0,1
| 0,05
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..
32. Дискретная случайная величина задана законом распределения
| Xi
| 2
| 3
| 5
|
| Pi
| 0, 5
| 0, 3
| 0, 2
|
Математическое ожидание равно…..
Дисперсия равна……..
Среднее квадратическое отклонение равно……..





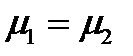
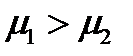
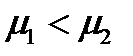

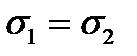
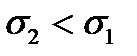
 0,5; 1 ]равна…...
0,5; 1 ]равна…...


