1. Равенство, содержащее дифференциал неизвестной функции.
2. Функция, удовлетворяющая данному уравнению.
3.Порядок наивысшей производной.
4.Среди предложенных ответов нет правильного.
22. ТОЧКА ДВИЖЕТСЯ ПО ЗАКОНУ S( t) =4 t3+ t2 +8(м). СКОРОСТЬ ДВИЖЕНИЯ ТОЧКИ В МОМЕНТВРЕМЕНИ t=2 с РАВНА….. м/с
1. 8 2. 52 3. 62 4. 74
| Инструкция для студентов. При выполнении задания следует написать только пропущенные требуемые слова или формулы, пронумеровав их. Объясните смысл, величин, входящих в формулу.
|
ДОПОЛНИТЕ
1. Геометрический смысл дифференциала функции
dy – это приращение………..(1)……….…(2) к графику
функции.
2.Градиент скалярной, функции – это ……..…..(1), характеризующий направление скорейшего ……..…..(2) функции.
3.ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ЭТО ……..(1), СОДЕРЖАЩЕЕ………(2) НЕИЗВЕСТНОЙ ФУНКЦИИ.
4.оБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ – ЭТО УРАВНЕНИЯ, В КОТОРЫХ ИСКОМАЯ ФУНКЦИЯ ЕСТЬ ФУНКЦИЯ…………..(1)……………(2)
| Инструкция для студентов. Задание состоит в выборе правильных пар из двух множеств. Каждому элементу левого задающего множества L соответствует определенный элемент или два (смотрите эталон ответа) правого множества выбора R.
|
УСТАНОВИТЕ СООТВЕТСТВИЕ
5. СООТВЕТСТВИЕ МЕЖДУ ВЕЛИЧИНОЙ И МАТЕМАТИЧЕСКИМ ВЫРАЖЕНИЕМ Для функции 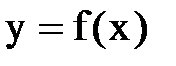
LR
| Величина
| Математическое выражение
|
| 1.Приращение аргумента.
2.Приращение функции.
3.Отношение приращения аргумента к приращению функции.
| А. 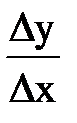 Б.
Б. 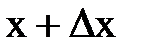 В.
В.  Д.
Д. 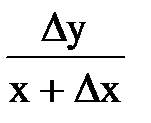 Е.
Е. 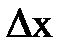 Ж
Ж 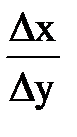
|
Эталон: 1_,2_,3_.
СООТВЕТСТВИЕ МЕЖДУФУНКЦИЕЙ И ЕЕ ПРОИЗВОДНОЙ
LR
| Функция у
| Производная функции 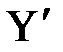
|
| 1. Sinx
2. Cosx
3. Sin2x
4. Sinx2
5. sin2x
| А. 2cos2x
Б. sinx
В. –sinx
Г. –cosx
Д. Cosx Е. 2xcosx2
Ж. 2sinx·cosx
З. cos2x
|
Эталон: 1_, 2_, 3_, 4_, 5_.
7. СООТВЕТСТВИЕ МЕЖДУ НАЗВАНИЯМИ И ЭЛЕМЕНТАМИ ФОРМУЛЫ dy= y' dx
LR
| Элементы формулы
| НАЗВАНИЕ
|
| 1. dy
2. y'
3. dx
| А. Дифференциал аргумента.
Б. Приращение функции.
В. Интеграл функции.
Г. Производная функции.
Д. Дифференциал функции.
|
Эталон: 1_, 2_, 3_.
8.СООТВЕТСТВИЕ МЕЖДУ ОБОЗНАЧЕНИЯМИ И НАЗВАНИЯМИ НеопределеннОГО интеграла 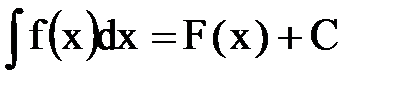
LR
| ОБОЗНАЧЕНИЕ
| Название
|
1. 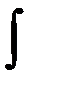 2. f(x)
3. f(x)dx
4. F(X).
5. C. Эталон: 1_, 2_, 3_, 4_, 5_.
2. f(x)
3. f(x)dx
4. F(X).
5. C. Эталон: 1_, 2_, 3_, 4_, 5_.
| А. Подынтегральное выражение.
Б. Константа интегрирования.
В. Подынтегральная функция.
Г. Первообразная..
Д. Интеграл
Ж. Производная функции
|
СООТВЕТСТВИЕ МЕЖДУ ИНТЕГРАЛОМ И ЕГО ЗНАЧЕНИЕМ
LR
| НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
| ЕГО ЗНАЧЕНИЕ
|
1. 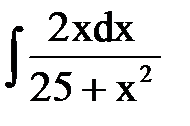 2.
2. 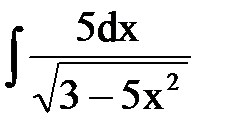
| А. 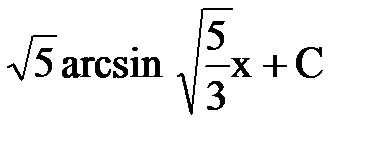 Б.
Б. 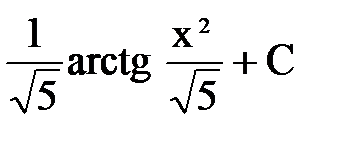 В.
В. 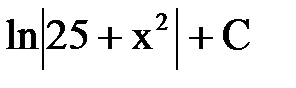 Г.
Г. 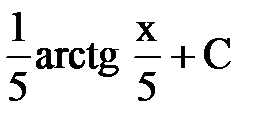
|
Эталон: 1_, 2_.
СООТВЕТСТВИЕ МЕЖДУ ИНТЕГРАЛОМ И ЕГО ЗНАЧЕНИЕМ
LR
| неопРЕДЕЛЕННЫЙ ИНТЕГРАЛ
| ЕГО ЗНАЧЕНИЕ
|
1. 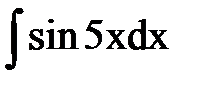 2.
2. 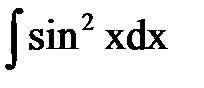
| А. 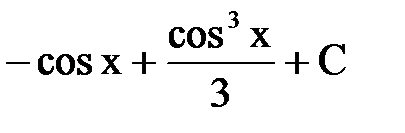 Б.
Б. 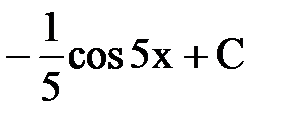 В.
В. 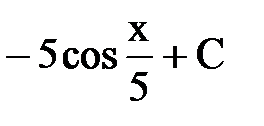 Г.
Г. 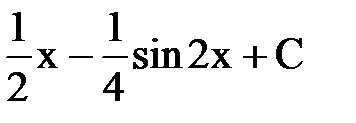
|
Эталон: 1_, 2_.
СООТВЕТСТВИЕ МЕЖДУ ИНТЕГРАЛОМИ ЕГО ЗНАЧЕНИЕМ
LR
| НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
| ЕГО ЗНАЧЕНИЕ
|
1.
2. 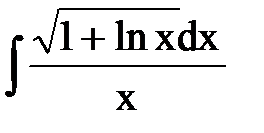 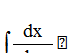
| А. 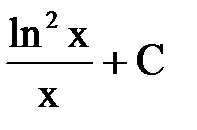 Б.
Б. 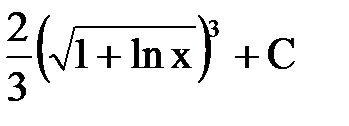 В.
В. 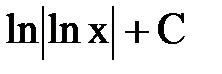 Г.
Г. 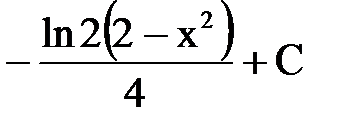
|
Эталон: 1_, 2_.
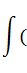
СООТВЕТСТВИЕ МЕЖДУ ИНТЕГРАЛОМ И ЕГО ЗНАЧЕНИЕМ
LR
| ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
| ЕГО ЗНАЧЕНИЕ
|
1. 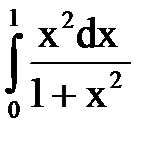 2.
2. 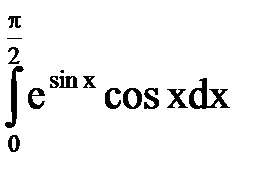
| А. 1,7
Б. 0,072
В. 0,2146
Г. 5,2
|
Эталон: 1_, 2_.
СООТВЕТСТВИЕ МЕЖДУ ИНТЕГРАЛОМ И ЕГО ЗНАЧЕНИЕМ
LR
| ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
| ЕГО ЗНАЧЕНИЕ
|
1. 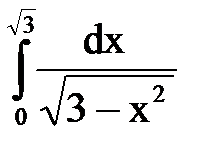 2.
2. 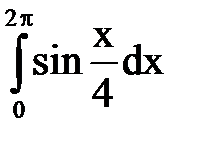
| А. 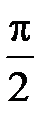 Б. 4
В. 8
Б. 4
В. 8
|
| Инструкция для студентов. В задании указать правильную последовательность упорядочиваемых элементов в специальной строке ответа-эталона.
|
УСТАНОВИТЕ ПРАВИЛЬНУЮ ПОСЛЕДОВАТЕЛЬНОСТЬ
ПОСЛЕДОВАТЕЛЬНОСТЬ ОПРЕДЕЛЕНИЯ. Градиент скалярной функции В ДАННОЙ ТОЧКЕ - ЭТО
1 – по длине, равный
2 – вектор, направленный по нормали
3 – производной данной функции по
4 – в сторону возрастания функции
5 – этому направлению.
6 – к поверхности уровня в этой точке
Эталон: _, _, _, _, _, _.
ПОСЛЕДОВАТЕЛЬНОСТЬ ОПРЕДЕЛЕНИЯ. Производная функции-это
1 – отношения.
2 – приращения функции  у
у
3 – при стремлении
4 – к нулю
5 – к приращению аргумента  х
х
6 – предел
7 – приращения аргумента  х
х
Эталон:_, _, _, _, _, _, _.
ПОСЛЕДОВАТЕЛЬНОСТЬ ОПРЕДЕЛЕНИЯ. Производной функции f( x, y) в точке М(х,у) по направлению l называется
1 – двух значений
2 – деленной на
3 – функции в некоторых двух точках
4 – этими точками
5 – предел разности
6 – расстояние междуЭталон:_, _, _, _, _, _.
ПОСЛЕДОВАТЕЛЬНОСТЬ ОПРЕДЕЛЕНИЯ. Определенный интеграл-это
1 – функции f(x)
2 – всех интегральных
3 – на отрезке (а,b)
4 – общий предел
5 – сумм
Эталон:_, _, _, _, _.
ПОСЛЕДОВАТЕЛЬНОСТЬ ОПРЕДЕЛЕНИЯ. согласно формуле Ньютона – Лейбница ДЛЯ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ДОСТАТОЧНО НАЙТИ.
1 – какой либо первообразной
2 – при верхнем и нижнем
3 – разность значений
4 – пределах интегрирования
5 – функции F(x) для f(x).
Эталон:_, _, _, _, _.





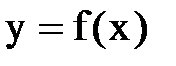
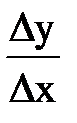 Б.
Б. 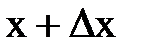 В.
В.  Д.
Д. 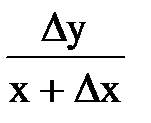 Е.
Е. 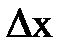 Ж
Ж 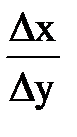
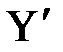
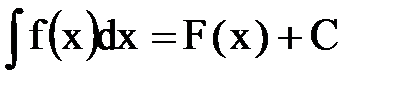
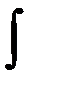 2. f(x)
3. f(x)dx
4. F(X).
5. C. Эталон: 1_, 2_, 3_, 4_, 5_.
2. f(x)
3. f(x)dx
4. F(X).
5. C. Эталон: 1_, 2_, 3_, 4_, 5_.
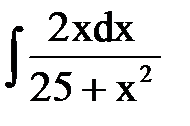 2.
2. 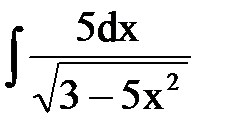
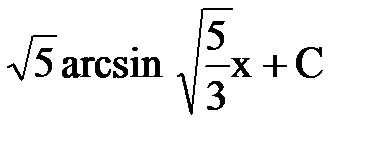 Б.
Б. 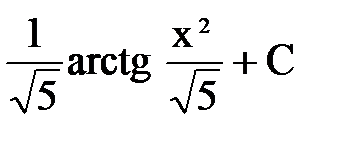 В.
В. 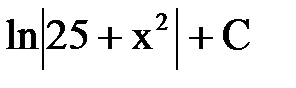 Г.
Г. 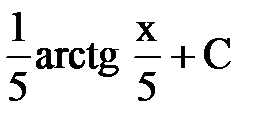
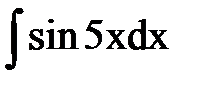 2.
2. 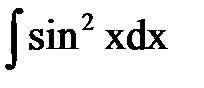
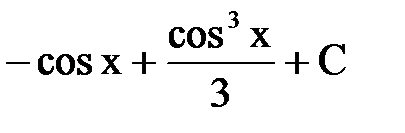 Б.
Б. 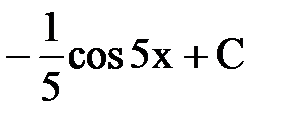 В.
В. 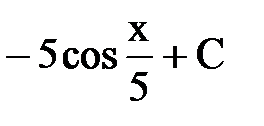 Г.
Г. 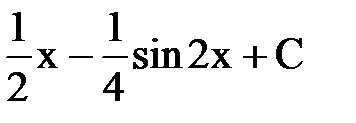
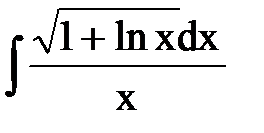
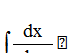
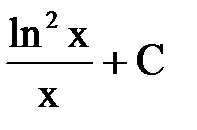 Б.
Б. 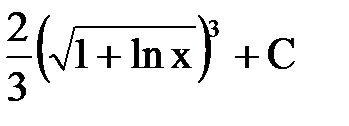 В.
В. 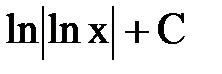 Г.
Г. 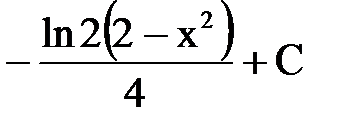
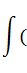
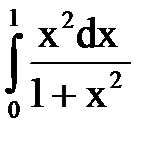 2.
2. 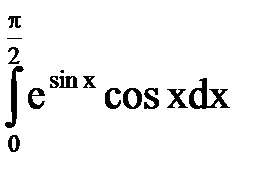
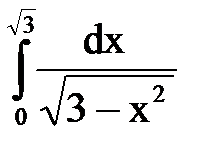 2.
2. 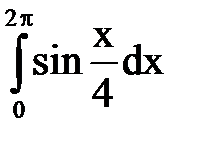
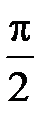 Б. 4
В. 8
Б. 4
В. 8
 у
у


