Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...
Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...
Топ:
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Дисциплины:
 2024-02-15 |
 64 |
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
L R
| КРИТЕРИЙ | ГИПОТЕЗА |
| 1. Кнабл³Ккр | А. Для параметрических критериев подтверждается Н0. |
| 2. Кнабл<Ккр | Б. Для параметрических критериев подтверждается Н1. |
| В.Для непараметрических критериев подтверждается Н0. | |
| Г. Для непараметрических крите- риев подтверждается Н1. |
Эталон: 1_,_,2_,_.
| Инструкция для студентов.В задании указать правильную последовательность упорядочиваемых элементов в специальной строке ответа-эталона. |
50.ПОСЛЕДОВАТЕЛЬНОСТЬ ОБЩЕЙ ПОСТАНОВКИ ЗАДАЧИ ПРОВЕРКИ ГИПОТЕЗ
1. По таблице находят Ккр
2. Выбирают критерий достоверности
3. Сравнивают Кнабли Ккр
4. Формулируют нулевую гипотезу
5. Вывод
6. Формулируют альтернативную гипотезу
7. По выборке определяют Кнабл
Эталон: _, _, _, _, _, _, _,_.
51. ПОСЛЕДОВАТЕЛЬНОСТЬ ДЕЙСТВИЙ ПРИ ПОСТРОЕНИИ ГИСТОГРАММЫ
1. Определяют количество выборочных данных в каждом классе
2. Определяют ширину классов и количество классов
3. Строят гистограмму
4. Диапазон измеряемой величины разбивают на равные интервалы
5. Устанавливают границы классов
Эталон: _, _, _, _, _.
52. ПОСЛЕДОВАТЕЛЬНОСТЬ ОПРЕДЕЛЕНИЯ: МОДА – ЭТО ……..
1. вероятности.
2. за ней варианты
3. имеют
4. такое значение
5. и следующая
6. меньше
7. варианты, что
8. предшествующая
Эталон: _, _, _, _, _, _,_, _.
ПОСЛЕДОВАТЕЛЬНОСТЬ ДЕЙСТВИЙ ПРИ СРАВНЕНИИ ГЕНЕРАЛЬНЫХ СРЕДНИХ ДВУХ НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
|
|
1. Зная a и f, находят по таблице tкр.
2. Выдвигают Н0 :m1 = m2.
3. Вывод.
4. Сравнивают tнабл и tкр.
5. Определяют по формуле tнабл.
6. Выдвигают Н1 :m1 ¹m2.
7. Определяют f.
Эталон: _, _, _, _, _, _, _.
ПОСЛЕДОВАТЕЛЬНОСТЬ ДЕЙСТВИЙ ПРИ СРАВНЕНИИ ГЕНЕРАЛЬНЫХ ДИСПЕРСИЙ ДВУХ НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
1. Выдвигают Н1: σ12> σ22
2. Определяют f1 , f2
3. СравниваютFнабл и Fкр
4. Зная a, f1 , f2 находят Fкр
5. Вывод
6. Выдвигают Н0 : σ12 = σ22 .
7. ОпределяютFнабл
Эталон: _, _, _, _, _, _, _.
ПОСЛЕДОВАТЕЛЬНОСТЬ ДЕЙСТВИЙ ПРИ ПРОВЕРКЕ ГИПОТЕЗ О ЗАКОНАХ РАСПРЕДЕЛЕНИЯ
1. Определяют χ2набл.
2. Вывод
3. Определяют f
4. Зная a и f, находят χ2кр
5. Выдвигают Н1
6. Сравнивают χ2набл и χ2кр
7. Выдвигают Н0. Эталон: _, _, _, _, _, _, _.
УСТАНОВИТЕ ПРИЧИННО - СЛЕДСТВЕННУЮ СВЯЗЬ
| Инструкция для студентов. При выполнении задания следует записать ответ, состоящий из трех пунктов. Схема ответа: • Высказывание А: верно/неверно; • Высказывание В: верно/неверно; • Связь : есть/нет. |
56. А. ЕСЛИ ПРИ ПРОВЕРКЕ ГИПОТЕЗ О РАВЕНСТВЕ ГЕНЕРАЛЬНЫХ ДИСПЕРСИЙ ПОДТВЕРЖДАЕТСЯ НУЛЕВАЯ ГИПОТЕЗА, ТО НЕЛЬЗЯ ПРИМЕНЯТЬ КРИТЕРИЙ СТЬЮДЕНТА ДЛЯ СРАВНЕНИЯ ГЕНЕРАЛЬНЫХ СРЕДНИХ.
ПОТОМУ ЧТО
Б. ОДНИМ ИЗ УСЛОВИЙ ПРИМЕНЕНИЯ КРИТЕРИЯ СТЬЮДЕНТА ДЛЯ СРАВНЕНИЯ ГЕНЕРАЛЬНЫХ СРЕДНИХ ЯВЛЯЕТСЯ РАВЕНСТВО ГЕНЕРАЛЬНЫХ ДИСПЕРСИЙ.
57. А. ДЛЯ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ МОДА И МЕДИАНА НЕ СОВПАДАЮТ С МАТЕМАТИЧЕСКИМ ОЖИДАНИЕМ
ПОТОМУ ЧТО
Б. ГРАФИК НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ СИММЕТРИЧЕН ОТНОСИТЕЛЬНО ПРЯМОЙ Х = m .
58. А. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ – ЭТО УСЛОВНОЕ ПОНЯТИЕ
ПОТОМУ ЧТО
Б. НА ПРАКТИКЕ БЫВАЕТ НЕВОЗМОЖНО ИССЛЕДОВАТЬ ВСЮ ГЕНЕРАЛЬНУЮ СОВОКУПНОСТЬ ОБЪЕКТОВ.
59. А. ПРИ УВЕЛИЧЕНИИ ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТИ ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ РАСШИРЯЕТСЯ
ПОТОМУ ЧТО
Б. ПРИ УВЕЛИЧЕНИИ ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТИ ВЕЛИЧИНА НОРМИРОВАННОГО ОТКЛОНЕНИЯ УМЕНЬШАЕТСЯ.
|
|
60. А. ЕСЛИ ПРИ СРАВНЕНИИ ГЕНЕРАЛЬНЫХ СРЕДНИХ ДВУХ НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН ПОДТВЕРЖДАЕТСЯ НУЛЕВАЯ ГИПОТЕЗА, ТО ВЫБОРКИ ПРИНАДЛЕЖАТ РАЗНЫМ ГЕНЕРАЛЬНЫМ СОВОКУПНОСТЯМ.
ПОТОМУ ЧТО
Б. НУЛЕВАЯ ГИПОТЕЗА ЗАКЛЮЧАЕТСЯ В ТОМ, ЧТО РАЗЛИЧИЕ ГЕНЕРАЛЬНЫХ СРЕДНИХ НЕЗНАЧИМО.
61. А. ЕСЛИ ПРИ СРАВНЕНИИ ГЕНЕРАЛЬНЫХ СРЕДНИХ ДВУХ НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН ПОДТВЕРЖДАЕТСЯ АЛЬТЕРНАТИВНАЯ ГИПОТЕЗА, ТО ВЫБОРКИ ПРИНАДЛЕЖАТ РАЗНЫМ ГЕНЕРАЛЬНЫМ СОВОКУПНОСТЯМ.
ПОТОМУ ЧТО
Б. АЛЬТЕРНАТИВНАЯ ГИПОТЕЗА ЗАКЛЮЧАЕТСЯ В ТОМ, ЧТО РАЗЛИЧИЕ ГЕНЕРАЛЬНЫХ СРЕДНИХ НЕЗНАЧИМО.
62. А. ЕСЛИ ПРИ ПРОВЕРКЕ ГИПОТЕЗ О РАВЕНСТВЕ ГЕНЕРАЛЬНЫХ ДИСПЕРСИЙ ПОДТВЕРЖДАЕТСЯ НУЛЕВАЯ ГИПОТЕЗА, ТО НЕЛЬЗЯ ПРИМЕНЯТЬ КРИТЕРИЙ СТЬЮДЕНТА ДЛЯ СРАВНЕНИЯ ГЕНЕРАЛЬНЫХ СРЕДНИХ.
ПОТОМУ ЧТО
Б. ОДНИМ ИЗ УСЛОВИЙ ПРИМЕНЕНИЯ КРИТЕРИЯ СТЬЮДЕНТА ДЛЯ СРАВНЕНИЯ ГЕНЕРАЛЬНЫХ СРЕДНИХ ЯВЛЯЕТСЯ РАВЕНСТВО ГЕНЕРАЛЬНЫХ ДИСПЕРСИЙ.
63. А. ЕСЛИ ПРИ ПРОВЕРКЕ ГИПОТЕЗ О РАВЕНСТВЕ ГЕНЕРАЛЬНЫХ ДИСПЕРСИЙ ПОДТВЕРЖДАЕТСЯ АЛЬТЕРНАТИВНАЯ ГИПОТЕЗА, ТО МОЖНО ПРИМЕНЯТЬ КРИТЕРИЙ СТЬЮДЕНТА ДЛЯ СРАВНЕНИЯ ГЕНЕРАЛЬНЫХ СРЕДНИХ.
ПОТОМУ ЧТО
Б. АЛЬТЕРНАТИВНАЯ ГИПОТЕЗА ЗАКЛЮЧАЕТСЯ В ТОМ, ЧТО РАЗЛИЧИЕ ГЕНЕРАЛЬНЫХ ДИСПЕРСИЙ НЕЗНАЧИМО.
64. А. ЕСЛИ ПРИ ПРОВЕРКЕ ГИПОТЕЗ О ЗАКОНАХ РАСПРЕДЕЛЕНИЯ ПОДТВЕРЖДАЕТСЯ НУЛЕВАЯ ГИПОТЕЗА, ТО НЕТ ПОДЧИНЕНИЯ РАССМАТРИВАЕМОМУ ЗАКОНУ РАСПРЕДЕЛЕНИЯ.
ПОТОМУ ЧТО
Б. НУЛЕВАЯ ГИПОТЕЗА ЗАКЛЮЧАЕТСЯ В ТОМ, ЧТО РАЗЛИЧИЕ МЕЖДУ ЭМПИРИЧЕСКИМИ И ТЕОРЕТИЧЕСКИМИ ЧАСТОТАМИ ЗНАЧИМО.
65. А. ЕСЛИ ПРИ ПРОВЕРКЕ ГИПОТЕЗ О ЗАКОНАХ РАСПРЕДЕЛЕНИЯ ПОДТВЕРЖДАЕТСЯ АЛЬТЕРНАТИВНАЯ ГИПОТЕЗА, ТО НЕТ ПОДЧИНЕНИЯ РАССМАТРИВАЕМОМУ ЗАКОНУ РАСПРЕДЕЛЕНИЯ.
ПОТОМУ ЧТО
Б. АЛЬТЕРНАТИВЕАЯ ГИПОТЕЗА ЗАКЛЮЧАЕТСЯ В ТОМ, ЧТО РАЗЛИЧИЕ МЕЖДУ ЭМПИРИЧЕСКИМИ И ТЕОРЕТИЧЕСКИМИ ЧАСТОТАМИ ЗНАЧИМО.
| Инструкция для студентов. При выполнении заданий запишите решение с полным его обоснованием. |
1. Из общего числа студентов выборочно измерен рост у 81 мужчины. Средний рост оказался равным 171 см с дисперсией S2 = 64 см2. Ошибка выборочного среднего равна…..Коэффициент вариации равен….
2. Содержание гемоглобина в крови, взятой у одной группы мужчин ( n1 = 40 ) оказалось равным в среднем 150. Тот же показатель для другой группы мужчин того же возраста (n2= 30) составил 160. Среднее значение изучаемой величины равно…, дисперсия равна…. и среднее квадратическое отклонение равно…...
|
|
3. Количественный признак Х распределен нормально. По выборке объема 18 найдено выборочное среднее значение 21,5 и среднее квадратическое отклонение S = 0,9. Коэффициент вариации равен….., ошибка выборочного среднего равна…… и доверительный интервал для математического ожидания при уровне значимости a£ 0,05 имеет вид…...
4. По данным девяти независимых равноточных измерений физической величины найдено среднее арифметическое результатов отдельных наблюдений 41,21 и исправленная дисперсия S2 = 25. Коэффициент вариации равен….., ошибка выборочного среднего равна….. и доверительный интервал для математического ожидания с доверительной вероятностью Р³ 0,99 имеет вид……...
5. При измерении содержания кальция (мг %) в сыворотке крови подопытных животных получили следующие результаты : 14,5 14,7 14,8 14,9 15,1 15,3 15,5 15,8 15,9. Интервальная оценка среднего значения соответствующей величины при уровне значимости a£ 0,05 имеет вид……...
6. При подсчете количества листьев у одного из лекарственных растений были получены следующие результаты: 5, 8, 10, 11, 12, 14. Интервальная оценка среднего значения соответствующей величины с доверительной вероятностью Р³ 0,95 имеет вид……...
7. Дан вариационный ряд:
Хi 25 28 30 32 34 36 40
ni 5 15 17 24 25 16 10
Мода равна………... Медиана равна……..
8. Дан вариационный ряд:
Хi 1 2 3 4 5 6
ni 5 10 10 25 40 10
Мода равна………... Медиана равна……..
9. Даны результаты измерений частоты сердечных сокращений у 13студентов перед началом занятий по физкультуре (выборка Х1 ) и у 12студентов после окончания занятий ( выборка Х2 ): оценки дисперсий соответственно равны S21= 79,6, S22 = 125,2. При уровне значимости a£ 0,05 проверьте гипотезу о равенстве генеральных дисперсий по результатам проведенных измерений.
10.Даны результаты измерений систолического давления в начальной стадии шока (мм рт. ст.) у 14 больных, оставшихся в живых после шока ( выборка Х1 ) и у 11 больных, умерших после шока ( выборка Х2 ): Х1ср= 137,3 , Х2ср= 86,5 . Расчетное значение t- критерия составило tэксп= 3,08. При уровне значимости a£ 0,05 определите значимость различия этих средних значений.
|
|
11.Даны результаты измерений частоты сердечных сокращений 11 студентов, проведенных сразу после окончания занятий по физкультуре
( выборка Х1 ) и 10 студентов - через 30 минут после окончания занятий по физкультуре ( выборка Х2): оценки дисперсий соответственно равны
S21= 139,9,S22 = 74,2. При уровне значимости a£ 0,05 проверьте гипотезу о равенстве генеральных дисперсий по результатам проведенных измерений.
12.Даны результаты измерений систолического давления в начальной стадии шока (мм рт. ст.) у 13 больных, оставшихся в живых (выборка Х1) и у 12 больных, умерших после шока (выборка Х2). Оценки дисперсий: дисперсии соответственно равны S21= 73,8, S22 = 116,9. При уровне значимости a £0,05 проверьте гипотезу о равенстве генеральных дисперсий по результатам проведенных измерений.
13.Даны результаты измерений среднего артериального давления (мм рт. ст. ) у 23 больных в начальной стадии шока ( выборка Х1 ) и у тех же 23 больных в конечной ( выборка Х2) стадиях шока: . Х 1ср= 85 , Х 2ср= 87 . Расчетное значение t- критерия составило tнабл = - 0,03. При уровне значимости a £0,05 определите значимость различия этих средних значений.
14.Средняя масса таблеток, найденная по выборке объемом 35 из первой партии, составила 0,5 г; по выборке объемом 40 из второй партии – 0,51 г. Расчетное значение t –критерия составило t набл = -1,52. При a ≤ 0,05 выясните, можно ли считать различие в средних значениях масс таблеток случайным.
15.Даны результаты измерений диастолического давления (мм рт. ст.) у 18 мужчин ( выборка Х1 ) и у 13 женщин ( выборка Х2 ): Х 1ср = 63,6 , Х 2ср= 31,5 . Расчетное значение t- критерия составило tнабл = 2,19.
При уровне значимости a£ 0,05 определите значимость различия этих средних значений.
16. Изучали влияние кобальта на массу тела кроликов. Опыт проводился на двух группах животных: опытной объемом 8и контрольной объемом 9. Опытные кролики в отличие от контрольных ежедневно получали добавку к рациону в виде хлористого кобальта по 0,06 г на 1 кг массы. За время опыта животные дали следующие прибавки живой массы тела: Х1= 638 г при дисперсии S12= 2596,3 г2 против Х2 = 626 г и дисперсии S22= 3579 г2 у контрольной группы. Можно ли для оценки достоверности этой разности использовать критерий Стьюдента?
Привести обоснование: расчеты с использованием критерия Фишера при a ≤ 0,05.
17.Изучали влияние эндотоксина на выживаемость облученных животных. В опытной группе было 36животных, выжило 23 (63,9%). В контрольной группе было 14 животных, выжило после облучения 3 (21,4%).
|
|
Можно ли судить о положительном влиянии эндотоксина на выживаемость животных, если наблюдаемое значениеt –критерия Стьюдентаtнабл= 2,71.
Уровень доверительной вероятности принять Р≥ 0,95.
18. Даны результаты измерений среднего артериального давления (мм рт. ст.) у 15 больных в начальной стадии шока ( выборка Х1 ) и у 15 больных в конечной ( выборка Х2 ) стадиях шока: Х 1ср = 99 , Х 2ср= 63 . Расчетное значение t- критерия составило tнабл = 2,47.
При уровне значимости a£ 0,05 определите значимость различия этих средних значений.
19.Даны результаты измерений систолического давления в начальной стадии шока (мм рт. ст.) у 21 больного, оставшихся в живых ( выборка Х 1 ) и у 12 больных, умерших после шока ( выборка Х 2): . Х 1ср = 124 ,
Х 2ср= 102 . Расчетное значение t- критерия составило tнабл = 0,37. При уровне значимости a£ 0,05 определите значимость различия этих средних значений.
20.Даны результаты измерений среднего артериального давления (мм рт. ст.) у 23 больных в начальной (выборкаХ 1) и у тех же 23 больных (выборка Х 2) в конечной стадиях шока: оценки дисперсий соответственно равны
S21= 270,2, S22 = 233,9.
При уровне значимости a£ 0,05 проверьте гипотезу о равенстве генеральных дисперсийпо результатам проведенных измерений.
21.Изучали влияние туберкулина на состав периферической крови низших обезьян: понижалось количество эозинофилов после введения туберкулина у большинства обезьян. Используя критерий знаков, получили следующие результаты: из 14 наблюдений 2 разности – нулевые, 10– положительные, 2 – отрицательные. При Р≥ 0,95 nкр = 12. Можно ли утверждать, что введение туберкулина вызывает снижение эозинофилов в периферической крови обезьян?
22.Изучали данные о годовых удоях коров и их потомства по второму и третьему отелам. При использовании критерия знаков получили следующие результаты: из 25 парных наблюдений положительная разница – в 12 случаях, отрицательная – в 13случаях. При Р≥ 0,95
nкр = 10. Сделайте вывод о достоверности различия между удоями коров материнского поколения и их потомства.
23.Даны результаты измерений среднего артериального давления (мм рт. ст. ) у 15 больных в начальной ( выборка Х 1 ) и у тех же 15 больных ( выборка
Х2 ) в конечной стадиях шока: оценки дисперсий соответственно равны S21= 28,8, S22 = 40,2. При уровне значимости a£ 0,05 проверьте гипотезу о равенстве генеральных дисперсий по результатам проведенных измерений.
24. Даны результаты измерений роста ( в см ) 19 детей ( выборка Х 1 ) и массы ( в кг ) 15 детей из той же группы: оценки дисперсий соответственно равны S21= 130,39, S22 = 32,98. При уровне значимости a£ 0,05 проверьте гипотезу о равенстве генеральных дисперсий по результатам проведенных измерений.
25. Даны результаты измерений пульса 13 студентов, проведенных перед началом занятий по физкультуре ( выборка Х1 ) и 12 студентов - после окончания занятий по физкультуре ( выборка Х2 ): Х1ср= 86 уд/мин , Х2ср= 152 уд/мин . Расчетное значение t- критерия составило tэксп= - 1,32. При уровне значимости a£ 0,05 определите значимость различия этих средних значений пульса.
26. Даны результаты измерений систолического давления в начальной стадии шока (мм рт. ст. ) у 13 больных, оставшихся в живых после шока ( выборка Х1 ) и у 12 больных, умерших после шока ( выборка Х2 ): Х1ср= 66 , Х2ср= 173 . Расчетное значение t- критерия составило tэксп= 3,59. При уровне значимости a£ 0,05 определите значимость различия этих средних значений.
27. Даны результаты измерений систолического давления в начальной стадии шока (мм рт. ст. ) у 14 больных, оставшихся в живых ( выборка Х1 ) и у 11 больных, умерших после шока ( выборка Х2 ): оценки дисперсий соответственно равны S21= 106,6, S22 = 40,9. При уровне значимости a£ 0,05 проверьте гипотезу о равенстве генеральных дисперсий по результатам проведенных измерений.
28.В таблице приведены эмпирические и вычисленные по нормальному закону частоты распределения длины тела у 267 мужчин. Из приведенных данных видно, что между этими частотами нет полного совпадения. При a ≤ 0,05 нужно установить, случайны или закономерны эти различия, т.е. следует ли это распределение роста мужчин нормальному закону. Расчет χ2 – критерия дал значение 1,47.
Эмпирические частоты 12 31 71 82 46 19 6
Теоретические частоты 12 34 68 78 51 20 5
29.В таблице приведены эмпирические и вычисленные по нормальному закону частоты распределения урожайности фасоли для 200 семян. При a ≤ 0,05 установить, случайны или закономерны эти различия, т.е. следует ли это распределение нормальному закону. Расчет χ2 – критерия дал значение 20,09.
Эмпирические частоты 1 5 17 45 70 51 10 1 0
Теоретические частоты 1 3 7 22 88 69 7 2 1
30.Даны результаты измерений пульса 11 студентов, проведенных сразу после окончания занятий по физкультуре ( выборка Х1 ) и 10 студентов - через 30 минут после окончания занятий по физкультуре ( выборка Х2 ):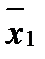 
= 140 уд/мин , 
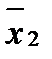= 74 уд/мин . Расчетное значение t- критерия составило tнабл = - 0,6. При уровне значимости a£ 0,05 определить значимость различия этих средних значений пульса.
31.Даны результаты измерений систолического давления в начальной стадии шока (мм рт. ст. ) у 21больного, оставшихся в живых ( выборка Х1 ) и у 12 больных, умерших после шока ( выборка Х2): оценки дисперсий соответственно равны S21 = 172,8, S22 = 161,4. При уровне значимости a£0,05 проверить гипотезу о равенстве генеральных дисперсий по результатам проведенных измерений.
32.Изучали систолическое давление в начальной стадии шока (ммрт.ст.) у людей, умерших после шока.Объем выборки n=12. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота
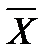= 101,83
79 – 90 0,16 S = 12,7
90 – 101 0,25
101 - 112 0,33 χ2 набл =1,36
112 – 123 0,25
· С α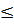 
0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р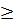 
0,95.
33.Изучали среднее артериальное давление в конечной стадии шока (ммрт.ст.). Объем выборки n=23. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота 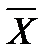= 8,21
51 – 64 0,04 S = 15,2
64 –77 0,17
77 - 90 0,34
90 - 103 0,3 χ2 набл =0,24
103 – 116 0,13
· С α 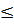0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р 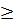0,95.
34. Изучали содержание магния (мг%) в сыворотке крови здоровых кроликов. Объем выборки n=10. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота 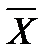= 10
9 - 9.5 0.2 S = 0,6
9.5 – 10 0.5
10 – 10.5 0.2 χ2 набл =0,09
10.5 - 11 0.11
· С α 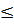0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р 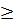0,95.
35.Изучали содержание кальция (мг%) в сыворотке крови больных обезьян. Объем выборки n=11. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота 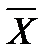= 6,86
5 - 5.75 0.09 S = 0,8
5.75 – 6.5 0.18
6.5 – 7.25 0.45
7.25 – 8 0.27 χ2 набл =0,47
· С α 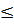0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р 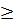0,95.
36. Изучали систолическое давление в начальной стадии шока (ммрт.ст.) у людей, оставшихся в живых. Объем выборки n=21. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота
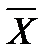= 123,95
93 - 105 0,04 S = 13,1
105 - 117 0,28
117 - 129 0,33
129 – 141 0,23
141 – 153 0,09 χ2 набл =1,03
· С α 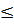0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р 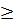0,95.
37.Изучали рост мужчин 25 лет (см) для городской местности.
Объем выборки n=19. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота
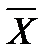= 170,15
160 –164 0,1 S = 4
164 – 168 0,15
168 - 172 0,36 χ2 набл =2,14
172 - 176 0,27
176 – 180 0,1
· С α 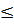0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервалдля математического ожидания с доверительной вероятностью Р 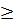0,95.
38.Изучали воздействие определенной физиопроцедуры
на частоту сердечных сокращений (уд\мин) у группы испытуемых. Объем выборки n=18. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота
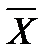= 70,16
67 –68,2 0,05 S = 1,2
68,2 – 69,4 0,16
69,4 – 70,6 0,44 χ2 набл =0,09
70,6 – 71,8 0,22
71,8 – 73,0 0,05
· С α 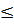0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервалдля математического ожидания с доверительной вероятностью Р 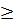0,95.
39.Изучали рост студентов колледжа (см). Объем выборки n=19. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота 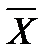= 170,15
160 –164 0.1 S = 4
164 – 168 0.15
168 - 172 0.36 χ2 набл =2,14
172 - 176 0.27
176 – 180 0.1
· С α 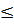0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р 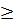0,95.
40.Изучали среднее артериальное давление в конечной стадии шока (ммрт.ст.). Объем выборки n=15. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота 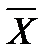= 99,86
89 – 94 0,06 S = 4,8
94 – 99 0,33
99 – 104 0,4
104 – 109 0,2 χ2 набл =0,4
· С α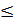 
0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р 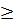0,95.
41.Изучали среднее артериальное давление в начальной стадии шока
(ммрт.ст.). Объем выборки n=23. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота 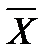= 85,04
59 - 70 0,17 S = 16,4
70 - 81 0,26
81 – 92 0,21
92 - 103 0,17 χ2 набл =0,35
103 -114 0,13
· С α 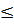0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р 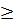0,95.
42. Изучали воздействие нового препарата на массу тела лабораторных мышей (г). Объем выборки n=9. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота 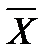= 74,11
64 – 68,75 0,12 S = 5,1
68,75 – 73,5 0,32 χ2 набл =3,51
73,5 – 78,25 0,42
78,25 - 83 0,13
· С α 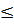0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервалдля математического ожидания с доверительной вероятностью Р 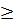0,95.
43.Изучали среднее артериальное давление в конечной стадии шока (ммрт.ст.). Объем выборки n=15.
Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота 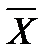= 63,46
51 – 57 0,13 S = 6,3
57 – 63 0,4
63 – 69 0,26
69 – 75 0,2 χ2 набл =0,45
· С α 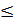0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р 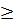0,95.
44.Изучали систолическое давление в начальной стадии шока
(ммрт.ст.). Объем выборки n=23. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота 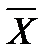= 121,5
92 – 106 0,09S =12,7
106 – 120025χ2 набл =0,4
120 – 134 0,39
134 – 148 0,14
· С α 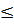0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р 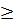0,95.
45.Изучали воздействие определенной физиопроцедуры на частоту сердечных сокращений (уд/мин) у группы испытуемых. Объем выборки n=16. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота 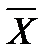= 70,75
67 –68,5 0,12S = 1,42
68,5 – 700,26
70– 71,50,48χ2 набл =0,09
71,5- 73,0 0,22
73– 74,5 0,07
· С α 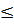0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р 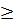0,95.
46.Изучали рост мужчин 25 лет (см) для сельской местности. Объем выборки n=21. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота
161 – 165 0,04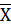 
= 171,42
165 –169 0,19 S = 3,6
169 – 173 0,47 χ2 набл =2,2
173 – 177 0,19
177 – 181 0,09
· С α 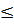0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р 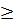0,95.
47. Изучали рост мужчин 30 лет (см) для сельской местности. Объем выборки n=24. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интервалов Частота
160 – 165 0,10 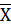= 172,5
165 –170 0,22 S = 2,9
170 – 175 0,51 χ2 набл =2,2
175 – 180 0,19
180 – 185 0,04
· С α 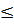0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервал для математического ожидания с доверительной вероятностью Р 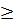0,95.
48. . Изучали воздействие нового препарата на массу тела лабораторных мышей (г). Объем выборки n=15. Проведена статистическая обработка данных.
РЕЗУЛЬТАТЫ РАСЧЕТА НА КОМПЬЮТЕРЕ
Границы интерваловЧастота 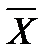= 68,5
60 – 64,25 0,14 S =4,6
64,25 – 68,5 0,38 χ2 набл =3,51
68,5 – 72,75 0,46
72,75 - 77 0,23
· С α 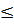0,05 выяснить, следует ли распределение нормальному закону.
· Построить гистограмму распределения частот.
· Определить доверительный интервалдля математического ожидания с доверительной вероятностью Р 0,95.
Биомеханика
| Инструкция для студентов. При выполнении заданий следует выбрать номер правильного ответа. Правильных ответов может быть несколько. |
ИНТЕНСИВНОСТЬ ЗВУКА
1. Плотность потока энергии звуковой волны.
2. Поток энергии звуковой волны.
3. Объемная плотность энергии звуковой волны.
4. Энергия звуковой волны.
2.ЭНЕРГИЯ В 100 Дж ПЕРЕНОСИТСЯ В ТЕЧЕНИЕ 5с ЧЕРЕЗ ПЛОЩАДКУ S=20м2, ПРИЧЕМ ПЛОЩАДКА ОРИЕНТИРОВАНА ПЕРПЕНДИКУЛЯРНО НАПРАВЛЕНИЮ РАСПРОСТРАНЕНИЯ ВОЛНЫ. ЗНАЧЕНИЕ ИНТЕНСИВНОСТИ ВОЛНЫ ПРИ ЭТОМ
1. 1 2. 5 3. 20 4. 10 000
3.АМПЛИТУДАЗВУКОВОЙ ВОЛНЫ УВЕЛИЧИЛАСЬ В 3 РАЗА. ЕЕ ИНТЕНИВНОСТЬ ВОЗРОСЛА В… РАЗА
1. 3 2. 6
3. 9 4. Не изменилась
4.АМПЛИТУДАЗВУКОВОЙ ВОЛНЫ УВЕЛИЧИЛАСЬ В 3 РАЗА. УРОВЕНЬ ГРОМКОСТИ УВЕЛИЧИЛСЯ ПРИМЕРНО НА……ДЕЦИБЕЛЛ
1. 3 2. 6
3. 10 4. 100
5.ГАРМОНИЧЕСКИЙСПЕКТРСЛОЖНОГО КОЛЕБАНИЯ – ЭТО ЗАВИСИМОСТЬ ОТЧАСТОТЫ
1. Амплитуды колебаний
2. Коэффициента затухания
3. Фазы колебаний
4. Смещения колеблющейся точки Х
ЧАСТОТА ОСНОВНОГОТОНА – ЭТО
1. Наибольшая частота спектра.
2. Средняя частота спектра.
3. Наименьшая частота спектра.
4. Среднее арифметическое наибольшей и наименьшей частоты.
ЧАСТОТЫ ОБЕРТОНОВ
1. Любые произвольные
2. Произвольные, но больше основной частоты
3. Кратные основной частоте
4. Произвольные, но меньше основной частоты
|
|
|
Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!
