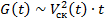Дополнительные главы обработки сейсмических данных
Основными учебными материалами по обработке сейсмических данных являются книгиЛ.Хаттона и О. Уилмаза.
Операции во временной области
Свертка – это математическая операция, которая двум функциям ставит в соответствие определенным образом вычисленную третью.
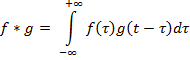
Свертка играет ключевую роль в электротехнике, так как с ее помощью описывается реакция линейной системы на входное воздействие, а также в сейсмике, поскольку в очень широком диапазоне условий земная толща ведет себя как линейная система.
Физический смысл свертки:

Свертку можно рассматривать как суперпозицию сдвинутых копий функции импульса сейсмического источника, умноженных на значения последовательных отсчетов коэффициентов отражения.
Система (среда) является предметом изучения.
Свойства свертки:
-линейность

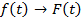
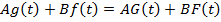
-стационарность (не изменяется по времени)
Функция источника:
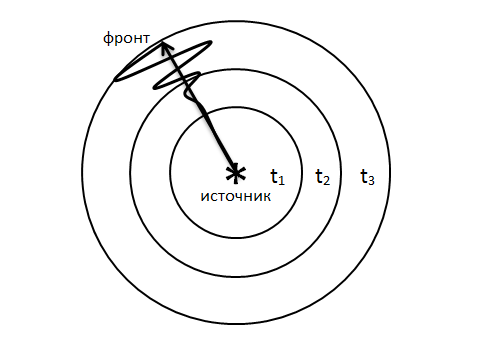
Уравнение для свертки в дискретном виде:
Последовательность, задающая входное воздействие (сигнал) - 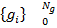 , где
, где

Последовательность, задающая характеристику среды - 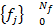 ,где
,где
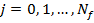
Последовательность, обозначающая сейсмическую трассу -  , где
, где


Пример:
Даны импульсная характеристика 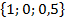 и сигнал
и сигнал 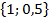 . Сделать их свертку.
. Сделать их свертку.
|
| 1
| 0
| 0,5
|
|
|
| 0,5
| 1
|
|
|
| 1
|
|
| 0,5
| 1
|
|
| 0,5
|
|
|
| 0,5
| 1
|
| 0,5
|
|
|
|
| 0,5
| 1
| 0,25
|
Свертка  .
.
Сверточная модель трассы
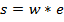
Свертку можно рассматривать как суперпозицию сдвинутых копий функции 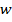 , умноженных на значения последовательных отсчетов
, умноженных на значения последовательных отсчетов  .
.
В сейсморазведке функцию 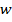 обычно интерпретируют как зондирующий импульс сейсмического источника, а
обычно интерпретируют как зондирующий импульс сейсмического источника, а  – как временную последовательность, связанную с распределением акустических жесткостей в среде. Вариации значений акустической жесткости приводят к образованию отражений, возвращающихся к поверхности земли. Функцию
– как временную последовательность, связанную с распределением акустических жесткостей в среде. Вариации значений акустической жесткости приводят к образованию отражений, возвращающихся к поверхности земли. Функцию  называют поэтому последовательностью коэффициентов отражения. Результат свертки
называют поэтому последовательностью коэффициентов отражения. Результат свертки 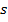 обозначает сейсмическую трассу.
обозначает сейсмическую трассу.
Используется модель среды, удовлетворяющая следующим условиям:
- слои горизонтальны;
- свойства постоянны;
- падает плоская волна;
- нормальное падение волны.
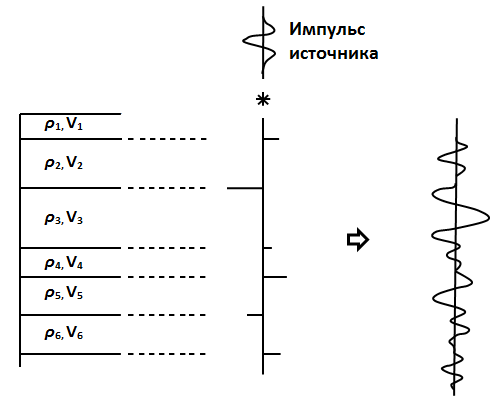
Формула для коэффициента отражения:
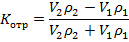
Выполняя операцию свертки коэффициентов отражения с исходным сигналом, получаем трассу:
Функция взаимной корреляции (ВКФ)
Взаимно-корреляционные функции используются для количественной оценки подобия между двумя временными рядами как функции временного сдвига между ними.


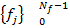

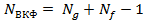

Пример:
Даны две последовательности 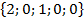 и
и 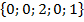 . Посчитать ВКФ.
. Посчитать ВКФ.
|
|
|
|
| 2
| 0
| 1
| 0
| 0
|
|
|
|
|
| T
|
| 0
| 0
| 2
| 0
| 1
|
|
|
|
|
|
|
|
| 2
| -4
|
|
| 0
| 0
| 2
| 0
| 1
|
|
|
|
|
|
|
| 0
| -3
|
|
|
| 0
| 0
| 2
| 0
| 1
|
|
|
|
|
|
| 5
| -2
|
|
|
|
| 0
| 0
| 2
| 0
| 1
|
|
|
|
|
| 0
| -1
|
|
|
|
|
| 0
| 0
| 2
| 0
| 1
|
|
|
|
| 2
| 0
|
|
|
|
|
|
| 0
| 0
| 2
| 0
| 1
|
|
|
| 0
| 1
|
|
|
|
|
|
|
| 0
| 0
| 2
| 0
| 1
|
|
| 0
| 2
|
|
|
|
|
|
|
|
| 0
| 0
| 2
| 0
| 1
|
| 0
| 3
|
|
|
|
|
|
|
|
|
| 0
| 0
| 2
| 0
| 1
| 0
| 4
|
ВКФ  , анализ ВКФ показывает, что функции на сдвиге
, анализ ВКФ показывает, что функции на сдвиге 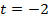 максимально коррелируют друг с другом.
максимально коррелируют друг с другом.
Свертка в матричном виде
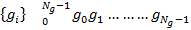

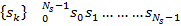
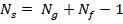
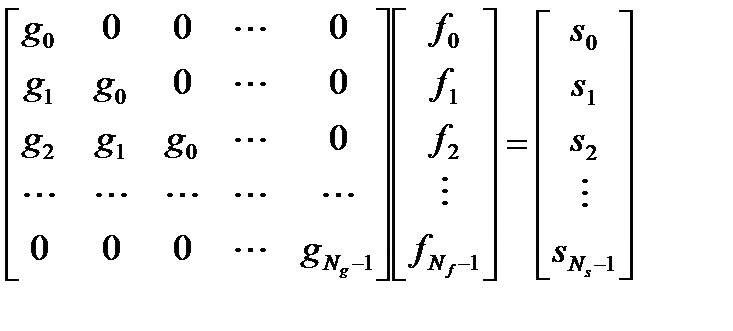
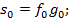

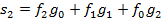
Преобразование Фурье
Преобразование Фурье выступает в трех общих формах, соответствующих трем классам функций:
1. Непрерывные периодические функции. Такие функции повторяются с некоторым периодом  . В этом случае функция представляется как дискретная бесконечная сумма, а коэффициенты Фурье выражаются через интегралы.
. В этом случае функция представляется как дискретная бесконечная сумма, а коэффициенты Фурье выражаются через интегралы.
2. Непрерывные непериодические функции. В этом случае и функция, и коэффициенты Фурье представляются интегралами.
3. Дискретные периодические и непериодические функции. В этом случае функция и коэффициенты Фурье представляются дискретными суммами.
Основной результат Фурье состоит в следующем. Пусть  –периодическая функция времени
–периодическая функция времени 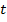 с периодом
с периодом  . Тогда
. Тогда 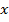 можно представить в виде бесконечного тригонометрического ряда.
можно представить в виде бесконечного тригонометрического ряда.
Свойства преобразования Фурье:
1) Линейность (следует из линейности интеграла):
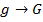
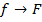
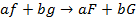
2) Запаздывание: 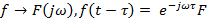
1. Преобразование Фурье для непрерывной периодической функции представляется в виде бесконечной суммы составляющих, а коэффициенты Фурье выражаются через интегралы:
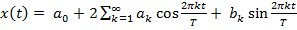 ;
;
Коэффициенты Фурье:
 ,
,
 ,
, 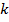 – номер гармоники.
– номер гармоники.
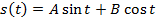
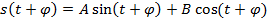
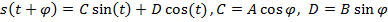 ,
, 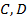 не зависят от
не зависят от 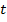
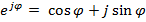
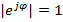 ,
, 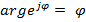
Преобразование Фурье в комплексном виде
Функция представляется в виде дискретной бесконечной суммы составляющих:
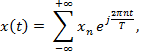
где 
2. Если функция непрерывная непериодическая, то и функция, и коэффициенты Фурье представляются интегралами:
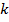 -eкоэффициенты
-eкоэффициенты 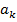 и
и 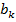 соответствуют стандартно определенной циклической частоте:
соответствуют стандартно определенной циклической частоте:
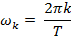
и расстояние между соседними суммируемыми частотными компонентами (разница двух гармоник) составляет:

при 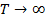 ,
, 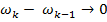
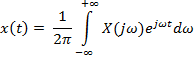
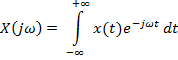
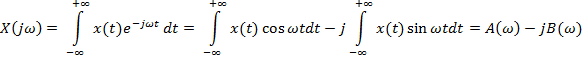
Амплитудный спектр = 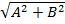
Фазовый спектр = 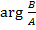 (изменяется в пределах от
(изменяется в пределах от 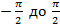 )
)
3. Дискретное преобразование Фурье (ДПФ)
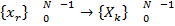
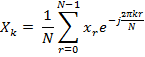
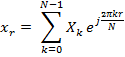
Свойства ДПФ
Периодичность: ДПФ периодично с периодом 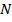 .
.

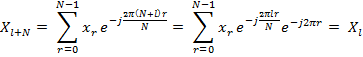
Вещественные временные ряды
Комплексное сопряжение: 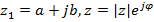 ,
,
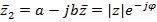
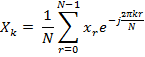
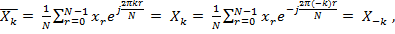 если
если 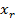 действительное.
действительное.
Таким образом, 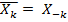
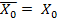 , т.е. компонента нулевой частоты (постоянная составляющая) вещественна и, поскольку вследствие периодичности
, т.е. компонента нулевой частоты (постоянная составляющая) вещественна и, поскольку вследствие периодичности 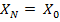 ,
, 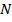 -я частотная компонента также вещественна.
-я частотная компонента также вещественна.
Из свойств сопряжения и периодичности получаем:
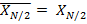 , т.е. компонента с номером
, т.е. компонента с номером 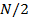 тоже имеет вещественное значение.
тоже имеет вещественное значение.
Используя вышеприведенные свойства, получаем симметрию спектра:
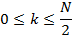
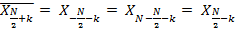
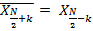
Каждой компоненте соответствует определенная частота. Компоненте с номером 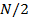 соответствует так называемая частота Найквиста.
соответствует так называемая частота Найквиста.
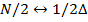
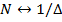 , где
, где  - шаг дискретизации
- шаг дискретизации
Теорема о свертке:
Пусть 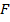 и
и 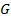 – дискретные преобразования Фурье последовательностей
– дискретные преобразования Фурье последовательностей 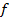 и
и 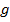 соответственно. Тогда:
соответственно. Тогда:
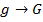 ,
, 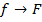
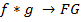
Т. е., свертка во временной области эквивалентна умножению соответствующих преобразований Фурье в частотной области.
Теорема о сдвиге:
По определению ДПФ:
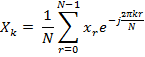
для 


Разбивая сумму на две части, от  до
до 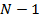 и от
и от 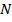 до
до 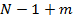 , и учитывая равенство
, и учитывая равенство
 , то получаем
, то получаем 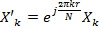 .
.
Интерполяция на основе преобразования Фурье:
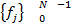 →преобразование Фурье→
→преобразование Фурье→ 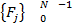 →берем половину спектра→
→берем половину спектра→ 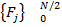 →
→
→делаем линейную интерполяцию→ 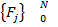 →обратное преобразование Фурье→
→обратное преобразование Фурье→ 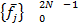
Нуль-фазовый сигнал:
В широком классе свойством минимальной длительности обладает сигнал с нулевым фазовым спектром. Такой сигнал симметричен относительно нулевого момента времени и, следовательно, не обладает свойством причинности. В идеальном случае он может продолжаться до бесконечности в обе стороны от нулевого момента времени.
Быстрое преобразование Фурье
Как следует из самого названия, БПФ – это просто изящный способ быстрого вычисления дискретного преобразования Фурье. Обычный алгоритм ДПФ требует для своего выполнения порядка 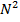 арифметических операций, тогда как при БПФ их требуется только
арифметических операций, тогда как при БПФ их требуется только 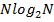 . При типичной для сейсморазведки значении
. При типичной для сейсморазведки значении 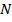 , равном 4096 отсчетов, БПФ вычисляется в 340 раз быстрее ДПФ.
, равном 4096 отсчетов, БПФ вычисляется в 340 раз быстрее ДПФ.

Количество точек во временной последовательности должно равняться степени двойки, для чего на практике последовательность обычно дополняют нулями.
z -преобразование
Рассмотрим временную последовательность с постоянным шагом дискретизации:
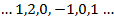
и построим следующий полином от  :
:
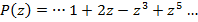
Этот полином и называется -преобразованием.
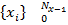
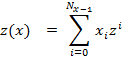
Свойство -преобразования:
если 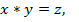 то
то 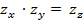
Таким образом, перемножение -преобразований эквивалентно свертке двух исходных последовательностей. Но, согласно теореме о свертке, этой операции эквивалентно и перемножение преобразований Фурье. Следовательно, преобразование Фурье временной последовательности можно рассматривать как частный случай -преобразования, когда
Влияние фазы сигнала

Свойства минимально-фазовых сигналов:
1) Реализуемые (импульс определяется как переходная форма волны конечной длины);
2) Причинные;
3) Максимум энергии находится в начале импульса;
4) АКФ сигналов с одинаковыми амплитудными спектрами равны.
Обратная фильтрация
Пусть заданы:
 – трасса
– трасса
 – импульс источника
– импульс источника
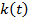 – коэффициенты отражения
– коэффициенты отражения
Тогда сейсмическая трасса представляет собой свертку импульса источника с коэффициентами отражения:

Задача обратной фильтрации:
Найти такой фильтр  , который при свертке с сигналом
, который при свертке с сигналом  дает дельта-функцию
дает дельта-функцию  . Тогда, в результате свертки этого фильтра с трассой, получаются коэффициенты отражения.
. Тогда, в результате свертки этого фильтра с трассой, получаются коэффициенты отражения.

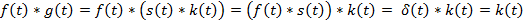
Блок-схема обратной фильтрации:

Рассмотрим пример обратной фильтрации для элементарного диполя:




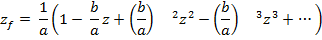
Если 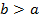 , то ряд расходится, тогда задача неустойчива (т.е. при малых изменениях начальных условий сильно меняется результат).
, то ряд расходится, тогда задача неустойчива (т.е. при малых изменениях начальных условий сильно меняется результат).
Пример 1:




Пример 2:

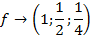

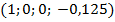
Пример 3:


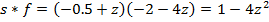
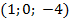
Метод наименьших квадратов
Когда входной импульс имеет вид, близкий к требуемому, например,  , в отличие от
, в отличие от  , обратная фильтрация дает хорошую аппроксимацию единичного импульса.
, обратная фильтрация дает хорошую аппроксимацию единичного импульса.
Можем ли мы улучшить результат?
При данном входном импульсе  найти такой двухэлементный фильтр
найти такой двухэлементный фильтр 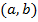 , чтобы ошибка между действительным и желаемым результатами
, чтобы ошибка между действительным и желаемым результатами 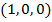 была минимальной с точки зрения метода наименьших квадратов. Рассчитаем действительный результат, свернув фильтр
была минимальной с точки зрения метода наименьших квадратов. Рассчитаем действительный результат, свернув фильтр 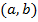 с входным импульсом
с входным импульсом  .
.



Ошибка  определяется как сумма квадратов разностей коэффициентов действительного и желаемого результатов:
определяется как сумма квадратов разностей коэффициентов действительного и желаемого результатов:

Задача состоит в том, чтобы найти такие коэффициенты  , чтобы
, чтобы  принимала минимальное значение. Упростив уравнение, взяв частные производные по
принимала минимальное значение. Упростив уравнение, взяв частные производные по  и
и 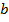 и задав результаты равные
и задав результаты равные  , получаем:
, получаем:

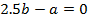
Имеется два уравнения и два неизвестных коэффициента фильтра. Так называемую нормальную систему уравнений можно привести в матричную форму:

Сейчас рассчитаем ВКФ желаемого результата  с входным импульсом
с входным импульсом 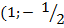 )
)

АКФ входного импульса равна:

Таким образом, в общем случае элементы матрицы в левой части – задержки АКФ входного импульса, а элементы матрицы, состоящей из одной колонки в правой части – это задержки ВКФ желаемого результата с входным импульсом.
Эти наблюдения были обобщены Винером для выведения фильтров, которые преобразуют входной сигнал в любой нужный выходной сигнал. Общая форма матричного уравнения для фильтра длины  .
.
Оптимальный фильтр Винера:

Здесь 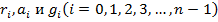 – ФАК входного импульса, коэффициенты желаемого фильтра и ФВК желаемого результата соответственно. Оптимальный фильтр Винера
– ФАК входного импульса, коэффициенты желаемого фильтра и ФВК желаемого результата соответственно. Оптимальный фильтр Винера  является оптимальным в том смысле, что ошибка, определенная по методу наименьших квадратов между действительным и желаемым результатами является минимальной. Когда желаемый результат представляет собой единичный импульс с нулевой задержкой
является оптимальным в том смысле, что ошибка, определенная по методу наименьших квадратов между действительным и желаемым результатами является минимальной. Когда желаемый результат представляет собой единичный импульс с нулевой задержкой 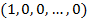 , фильтр Винера идентичен обратному фильтру, действующему по принципу наименьших квадратов. Другими словами, последний является специальным случаем первого. Фильтр Винера применяется для решения большого класса задач, в которых может быть рассмотрен любой желаемый результат, а не только единичный импульс с нулевой задержкой.
, фильтр Винера идентичен обратному фильтру, действующему по принципу наименьших квадратов. Другими словами, последний является специальным случаем первого. Фильтр Винера применяется для решения большого класса задач, в которых может быть рассмотрен любой желаемый результат, а не только единичный импульс с нулевой задержкой.
Деконволюция
Модель фильтрации зарегистрированной сейсмограммы описывается уравнением:

где  – зарегистрированная сейсмограмма,
– зарегистрированная сейсмограмма,  – основной сейсмический импульс,
– основной сейсмический импульс,  – импульсный отклик разреза,
– импульсный отклик разреза, 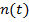 – случайная помеха, * - обозначение деконволюции.
– случайная помеха, * - обозначение деконволюции.
Деконволюция пытается восстановить последовательность коэффициентов отражения (или импульсный отклик) по зарегистрированной сейсмограмме.
Блок-схема деконволюции:
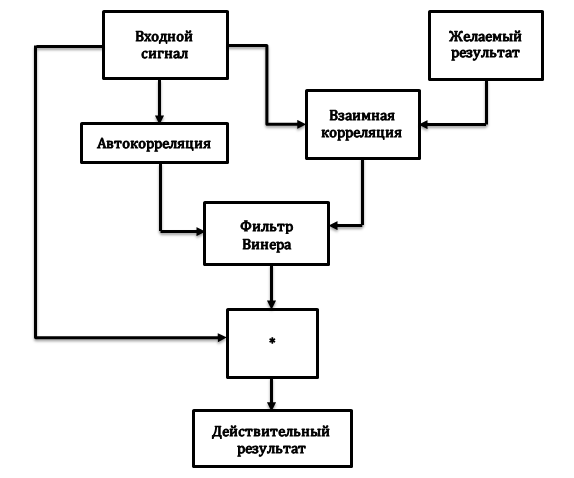
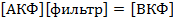
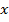 – входной импульс
– входной импульс
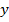 – желаемый выходной сигнал
– желаемый выходной сигнал
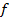 -?
-?

Варианты желаемого результата деконволюции:
1)  -импульс (единичный импульс с нулевой задержкой);
-импульс (единичный импульс с нулевой задержкой);
2) сдвинутый -импульс (единичный импульс с произвольной задержкой);
3) сдвинутая входная трасса;
4) нуль-фазовый сигнал;
5) любая произвольная форма.
Достижение результатов 1-2 называют деконволюцией сжатия. Результат 3 – итог предсказывающей деконволюции, результат 4 – пиковой деконволюции и результат 5 – формирующей.
Ограничения, лежащие в основе деконволюции:
1) Разрез состоит из горизонтальных слоев с постоянной скоростью;
2) Источник формирует плоскую продольную волну, которая вертикально падает на границы слоев. При таких условиях поперечные волны не формируются;
3) Форма волны источника не меняется при прохождении по разрезу, т.е. она является стационарной;
4) Компонента помех равна 0;
5) Сейсмический импульс является минимально-фазовым;
6) Коэффициенты отражения являются случайным процессом.
Деконволюция сжатия
Процесс с единичным импульсом с единичной задержкой называется деконволюцией сжатия. Взаимная корреляция желаемого единичного импульса 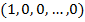 со входным импульсом (
со входным импульсом ( дает последовательность (
дает последовательность (

Деконволюция сжатия с математической точки зрения идентична обратной фильтрации по методу наименьших квадратов. В идеальном случае мы хотим получить одиночный импульс с нулевой задержкой, но, обычно, входной импульс – смешанно-фазовый сигнал. Если входной импульс не является минимально-фазовым, деконволюция сжатия не может преобразовать его в совершенный единичный импульс с нулевой задержкой. Хотя амплитудный спектр, в сущности, плоский, фазовый спектр результата не является минимально-фазовым. Оператор деконволюции сжатия представляет собой результат обращения минимально-фазового эквивалента входного импульса. Этот импульс может быть минимально-фазовым, но может и не быть таковым.
Предварительное отбеливание
Деконволюция отфильтрованного импульса не дает совершенный единичный импульс. Вместо этого получается единичный шаг-импульс, сопровождаемый высокими частотами. Такой низкочастотный результат обусловлен тем, что оператор деконволюции пытается усилить отсутствующие частоты. Может ли эта проблема быть связана с зарегистрированной сейсмограммой? Ситуация, когда амплитудный спектр входного сигнала содержит нули, встречается редко. В сейсмограмме всегда содержатся помехи и они являются аддитивными во временной и в частотной областях. Более того, в процессе обработки формируются цифровые помехи, также являющиеся аддитивными в частотной области. Однако, для того, чтобы гарантировать цифровую устойчивость, перед деконволюцией вводится искусственный уровень белого шума. Этот процесс называется предварительным отбеливанием. Оно достигается путем прибавления константы к нулевой задержке функции автокорреляции.



Двумерная фильтрация
В сейсмике чаще всего приходится иметь дело с двумерными преобразованиями, у которых одна координата временная, а другая пространственная. Соответствующую область частот обычно называют - плоскостью, где 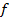 - временная и
- временная и 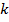 - пространственная частоты.
- пространственная частоты.
Двумерная фильтрация – это распространение на двумерный случай одномерной фильтрации. Например, двумерная свертка эквивалентна перемножению двумерных спектров. Таким образом, двумерную фильтрацию можно реализовать, если построить подходящий спектр фильтра в двумерной частотной области и умножить его на двумерное преобразование Фурье входных данных.
Фильтрация в 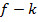 - области привлекательна тем, что в отличие от одного измерения, где сигнал и помеха могут перекрываться, делая одномерную фильтрацию неэффективной, в двух измерениях они обычно не перекрываются по
- области привлекательна тем, что в отличие от одного измерения, где сигнал и помеха могут перекрываться, делая одномерную фильтрацию неэффективной, в двух измерениях они обычно не перекрываются по 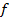 и
и 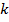 одновременно.
одновременно.
Рассмотрим следующую двумерную функцию:
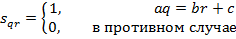
где 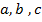 – постоянные коэффициенты, задающие прямую в плоскости
– постоянные коэффициенты, задающие прямую в плоскости 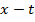 с тангенсом угла наклона
с тангенсом угла наклона  .
.
Делаем двумерное преобразование Фурье:
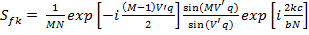 , где
, где 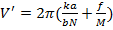
При 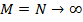 :
:
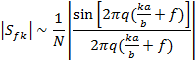
В пределе получаем, что вся энергия концентрируется вдоль прямой 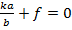 .
.
Это и есть желаемый результат. Коэффициент с определяет только фазу сигнала.
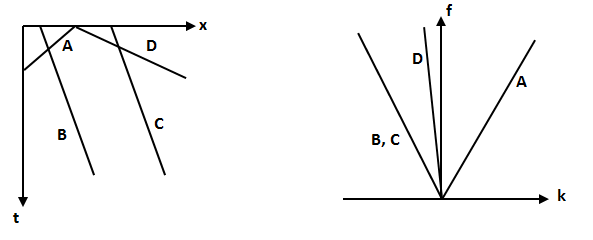
На рисунке показаны некоторые прямые и их двумерные спектры в том виде, как они обычно изображаются в сейсмике (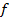 меняется от нуля до временной частоты Найквиста
меняется от нуля до временной частоты Найквиста 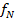 и
и 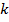 меняется от
меняется от 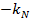 до
до 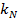 , где
, где 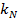 – пространственная частота Найквиста). Поскольку коэффициент
– пространственная частота Найквиста). Поскольку коэффициент 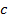 входит только в фазу двумерного спектра, прямые В и С отображаются на
входит только в фазу двумерного спектра, прямые В и С отображаются на 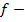 - плоскости в одну и ту же прямую линию. Все такие прямые в
- плоскости в одну и ту же прямую линию. Все такие прямые в 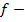 - плоскости проходят через начало координат. Кроме того, крутым наклонам в
- плоскости проходят через начало координат. Кроме того, крутым наклонам в 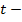 - области (т.е. большим значениям
- области (т.е. большим значениям 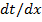 ) соответствуют пологие наклоны на
) соответствуют пологие наклоны на 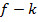 - плоскости (малые значения
- плоскости (малые значения 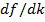 ).
).
Наклонная прямая 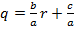 в
в 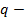 - области (эквивалентной
- области (эквивалентной 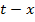 ) отображается в наклонную прямую
) отображается в наклонную прямую 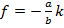 на плоскости
на плоскости 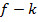 .
.
Эти уравнения дают связь между временной и пространственной координатами, из которой скорость можно определить как 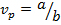 , где
, где 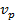 – фазовая (кажущаяся) скорость.
– фазовая (кажущаяся) скорость.
Поскольку наклонная прямая в области 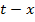 переходит в наклонную прямую на плоскости
переходит в наклонную прямую на плоскости 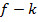 , прямолинейные оси синфазности в заданном диапазоне наклонов можно подавить с помощью фильтра, двумерное преобразование Фурье которого равно нулю в интервале между соответствующими наклонами на
, прямолинейные оси синфазности в заданном диапазоне наклонов можно подавить с помощью фильтра, двумерное преобразование Фурье которого равно нулю в интервале между соответствующими наклонами на 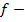 - плоскости и единице вне его. Такой фильтр обычно называют веерным.
- плоскости и единице вне его. Такой фильтр обычно называют веерным.
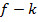 - фильтрация используется, в особенности, при обработке скважинной сейсморазведки (метод ВСП). В наземной сейсморазведке такая фильтрация используется для подавления поверхностных волн.
- фильтрация используется, в особенности, при обработке скважинной сейсморазведки (метод ВСП). В наземной сейсморазведке такая фильтрация используется для подавления поверхностных волн.
Преобразование Радона
Преобразование Радона — интегральное преобразование функции многих переменных, родственное преобразованию Фурье.Важнейшее свойство преобразования Радона — обратимость, то есть возможность восстанавливать исходную функцию по её преобразованию Радона.
Пусть 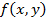 – функция двух действительных переменных, определенная на всей плоскости и достаточно быстро убывающая на бесконечности. Тогда преобразованием Радона функции
– функция двух действительных переменных, определенная на всей плоскости и достаточно быстро убывающая на бесконечности. Тогда преобразованием Радона функции 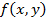 называется функция:
называется функция:
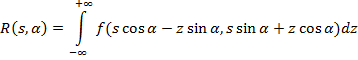
Преобразование Радона имеет простой геометрический смысл – это интеграл от функции вдоль прямой, перпендикулярной вектору  и проходящей на расстоянии
и проходящей на расстоянии 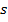 от начала координат.
от начала координат.
Преобразование можно записать и в другом виде, записывая уравнение прямой в виде 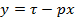 . Тогда преобразование Радона выглядит:
. Тогда преобразование Радона выглядит:
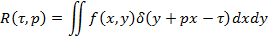
Когда 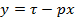 ,
, 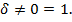
Связь преобразования Радона (ПР) с преобразованием Фурье (ПФ):
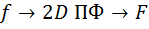
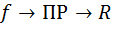
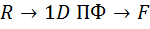
Таким образом, одномерноепреобразование Фурье от преобразования Радона для функции 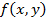 есть не что иное какдвумерноепреобразование Фурье от функции
есть не что иное какдвумерноепреобразование Фурье от функции 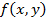 .
.
Преобразование Радона, главным образом, используется в медицине (компьютерная рентгеновская томография). Иногда ПР применяют в геофизической томографии.
Также существует гиперболическое преобразование Радона:
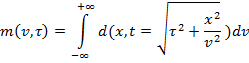
Основная техническая проблема преобразований Радона – их неустойчивость. Для ее решения применяют алгоритмы регуляризации: наименьших квадратов и «высокоразрешающий».
Способы удаления кратных волн:
1) методы, использующие периодические свойства кратных волн (предсказывающая деконволюция);
2) методы, использующие кривизну годографов кратных волн (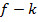 - фильтрация, преобразование Радона);
- фильтрация, преобразование Радона);
3) продолжение волнового поля;
4) SRME.
Факторы, влияющие на амплитуду:
1) поглощение;
2) рассеяние;
3) расхождение;
4) потери энергии при прохождении границ.
Сферическое расхождение
Затухание амплитуды с удалением от источника происходит по следующим законам:
для поверхностной волны - 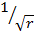 ;
;
для головной волны - 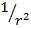 ;
;
для остальных типов волн - 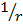 ;
;
Для компенсации сферического расхождения можно использовать масштабный множитель 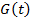 , пропорциональный
, пропорциональный 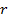 :
:
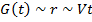 (для среды с постоянной скоростью)
(для среды с постоянной скоростью)
Если рассматривать случай слоистой среды с переменной скоростью и с учетом преломления, в качестве 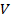 должна использоваться среднеквадратичная скорость
должна использоваться среднеквадратичная скорость 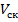 :
:
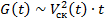
Обычно, амплитудный уровень сейсмических записей требуется сделать всюду примерно одинаковым. Кроме того, при контроле качества обработки необходимо приводить записи к динамическому диапазону, пригодному для их визуализации.
Способы восстановления амплитуды:
1) усиление;
2) компенсация за сферическое расхождение;
3) АРУ.
Разнообразные процедуры выравнивания амплитуд можно разделить на две категории:
1) Выравнивание, не зависящее от данных.
Это такие процедуры, в которых ко всем трассам применяется одна и та же масштабирующая кривая, полученная осреднением по большому массиву данных. Таким образом, масштабный множитель каждого конкретного отсчета не зависит ни от его собственного значения, ни от среднего значения соседних отсчетов.
2) Выравнивание, зависящее от данных.
Когда вариации амплитудного уровня велики и непредсказуемы, выравнивание записи путем умножения на единую для профиля масштабирующую функцию может оказаться недостаточным. В этом случае целесообразно применять индивидуальные масштабирующие функции потрассно. Процедуры выравнивания амплитудного уровня, в которых каждый отсчет записи умножается на масштабный коэффициент, величина которого определяется значениями в окрестности данного отсчета, объединяют



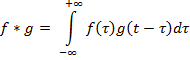


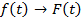
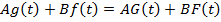

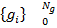 , где
, где
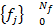 ,где
,где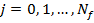
 , где
, где

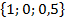 и сигнал
и сигнал 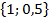 . Сделать их свертку.
. Сделать их свертку. .
.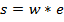
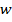 , умноженных на значения последовательных отсчетов
, умноженных на значения последовательных отсчетов  .
.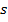 обозначает сейсмическую трассу.
обозначает сейсмическую трассу.
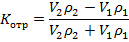


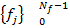

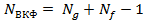

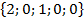 и
и 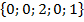 . Посчитать ВКФ.
. Посчитать ВКФ. , анализ ВКФ показывает, что функции на сдвиге
, анализ ВКФ показывает, что функции на сдвиге 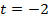 максимально коррелируют друг с другом.
максимально коррелируют друг с другом.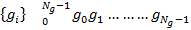

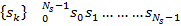
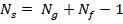
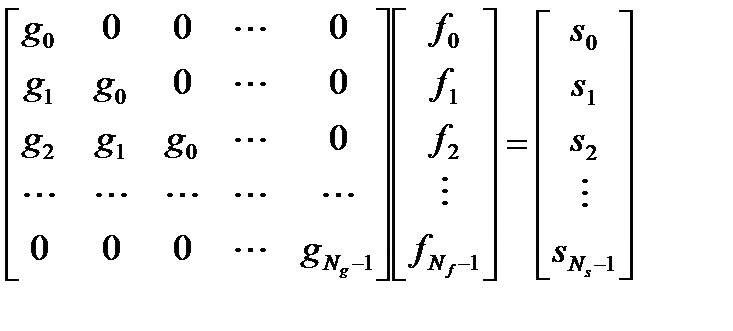
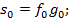

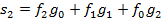
 . В этом случае функция представляется как дискретная бесконечная сумма, а коэффициенты Фурье выражаются через интегралы.
. В этом случае функция представляется как дискретная бесконечная сумма, а коэффициенты Фурье выражаются через интегралы. –периодическая функция времени
–периодическая функция времени 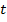 с периодом
с периодом 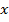 можно представить в виде бесконечного тригонометрического ряда.
можно представить в виде бесконечного тригонометрического ряда.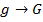
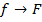
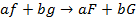
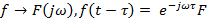
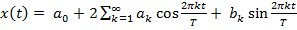 ;
; ,
, ,
, 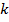 – номер гармоники.
– номер гармоники.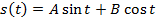
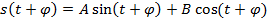
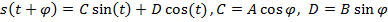 ,
, 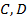 не зависят от
не зависят от 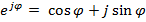
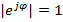 ,
, 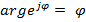
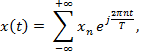

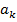 и
и 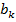 соответствуют стандартно определенной циклической частоте:
соответствуют стандартно определенной циклической частоте: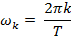

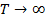 ,
, 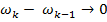
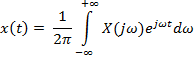
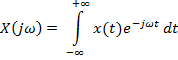
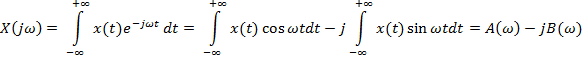
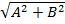
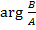 (изменяется в пределах от
(изменяется в пределах от 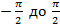 )
)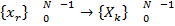
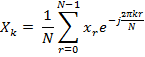
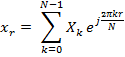
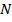 .
.
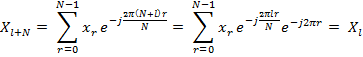
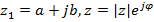 ,
,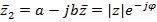
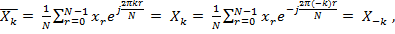 если
если 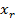 действительное.
действительное.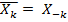
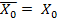 , т.е. компонента нулевой частоты (постоянная составляющая) вещественна и, поскольку вследствие периодичности
, т.е. компонента нулевой частоты (постоянная составляющая) вещественна и, поскольку вследствие периодичности 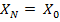 ,
, 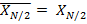 , т.е. компонента с номером
, т.е. компонента с номером 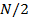 тоже имеет вещественное значение.
тоже имеет вещественное значение.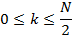
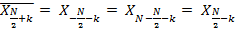
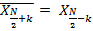
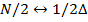
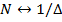 , где
, где  - шаг дискретизации
- шаг дискретизации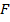 и
и 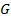 – дискретные преобразования Фурье последовательностей
– дискретные преобразования Фурье последовательностей 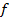 и
и 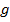 соответственно. Тогда:
соответственно. Тогда: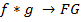



 до
до 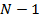 и от
и от 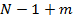 , и учитывая равенство
, и учитывая равенство , то получаем
, то получаем 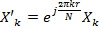 .
.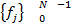 →преобразование Фурье→
→преобразование Фурье→ 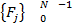 →берем половину спектра→
→берем половину спектра→ 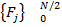 →
→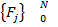 →обратное преобразование Фурье→
→обратное преобразование Фурье→ 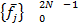
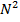 арифметических операций, тогда как при БПФ их требуется только
арифметических операций, тогда как при БПФ их требуется только 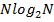 . При типичной для сейсморазведки значении
. При типичной для сейсморазведки значении 
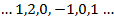
 :
: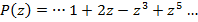
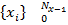
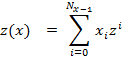
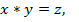 то
то 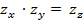
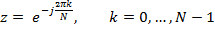

 – трасса
– трасса – импульс источника
– импульс источника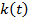 – коэффициенты отражения
– коэффициенты отражения
 , который при свертке с сигналом
, который при свертке с сигналом  . Тогда, в результате свертки этого фильтра с трассой, получаются коэффициенты отражения.
. Тогда, в результате свертки этого фильтра с трассой, получаются коэффициенты отражения.
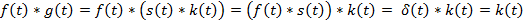





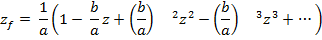
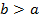 , то ряд расходится, тогда задача неустойчива (т.е. при малых изменениях начальных условий сильно меняется результат).
, то ряд расходится, тогда задача неустойчива (т.е. при малых изменениях начальных условий сильно меняется результат).



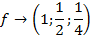

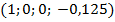


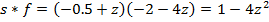
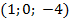
 , в отличие от
, в отличие от  , обратная фильтрация дает хорошую аппроксимацию единичного импульса.
, обратная фильтрация дает хорошую аппроксимацию единичного импульса.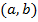 , чтобы ошибка между действительным и желаемым результатами
, чтобы ошибка между действительным и желаемым результатами 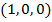 была минимальной с точки зрения метода наименьших квадратов. Рассчитаем действительный результат, свернув фильтр
была минимальной с точки зрения метода наименьших квадратов. Рассчитаем действительный результат, свернув фильтр 

 определяется как сумма квадратов разностей коэффициентов действительного и желаемого результатов:
определяется как сумма квадратов разностей коэффициентов действительного и желаемого результатов:
 , чтобы
, чтобы  и
и 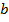 и задав результаты равные
и задав результаты равные  , получаем:
, получаем:
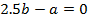

 с входным импульсом
с входным импульсом 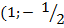 )
)

 .
.
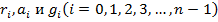 – ФАК входного импульса, коэффициенты желаемого фильтра и ФВК желаемого результата соответственно. Оптимальный фильтр Винера
– ФАК входного импульса, коэффициенты желаемого фильтра и ФВК желаемого результата соответственно. Оптимальный фильтр Винера  является оптимальным в том смысле, что ошибка, определенная по методу наименьших квадратов между действительным и желаемым результатами является минимальной. Когда желаемый результат представляет собой единичный импульс с нулевой задержкой
является оптимальным в том смысле, что ошибка, определенная по методу наименьших квадратов между действительным и желаемым результатами является минимальной. Когда желаемый результат представляет собой единичный импульс с нулевой задержкой 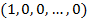 , фильтр Винера идентичен обратному фильтру, действующему по принципу наименьших квадратов. Другими словами, последний является специальным случаем первого. Фильтр Винера применяется для решения большого класса задач, в которых может быть рассмотрен любой желаемый результат, а не только единичный импульс с нулевой задержкой.
, фильтр Винера идентичен обратному фильтру, действующему по принципу наименьших квадратов. Другими словами, последний является специальным случаем первого. Фильтр Винера применяется для решения большого класса задач, в которых может быть рассмотрен любой желаемый результат, а не только единичный импульс с нулевой задержкой.
 – зарегистрированная сейсмограмма,
– зарегистрированная сейсмограмма,  – основной сейсмический импульс,
– основной сейсмический импульс,  – импульсный отклик разреза,
– импульсный отклик разреза, 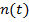 – случайная помеха, * - обозначение деконволюции.
– случайная помеха, * - обозначение деконволюции.
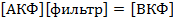
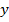 – желаемый выходной сигнал
– желаемый выходной сигнал
 -импульс (единичный импульс с нулевой задержкой);
-импульс (единичный импульс с нулевой задержкой);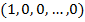 со входным импульсом (
со входным импульсом ( дает последовательность (
дает последовательность (




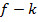 - области привлекательна тем, что в отличие от одного измерения, где сигнал и помеха могут перекрываться, делая одномерную фильтрацию неэффективной, в двух измерениях они обычно не перекрываются по
- области привлекательна тем, что в отличие от одного измерения, где сигнал и помеха могут перекрываться, делая одномерную фильтрацию неэффективной, в двух измерениях они обычно не перекрываются по 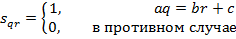
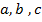 – постоянные коэффициенты, задающие прямую в плоскости
– постоянные коэффициенты, задающие прямую в плоскости 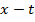 с тангенсом угла наклона
с тангенсом угла наклона  .
.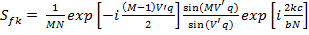 , где
, где 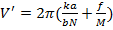
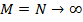 :
: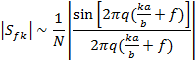
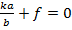 .
.
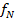 и
и 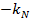 до
до 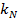 , где
, где 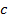 входит только в фазу двумерного спектра, прямые В и С отображаются на
входит только в фазу двумерного спектра, прямые В и С отображаются на 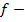 - плоскости в одну и ту же прямую линию. Все такие прямые в
- плоскости в одну и ту же прямую линию. Все такие прямые в 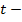 - области (т.е. большим значениям
- области (т.е. большим значениям 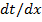 ) соответствуют пологие наклоны на
) соответствуют пологие наклоны на 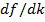 ).
).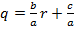 в
в 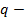 - области (эквивалентной
- области (эквивалентной 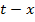 ) отображается в наклонную прямую
) отображается в наклонную прямую 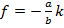 на плоскости
на плоскости 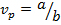 , где
, где 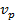 – фазовая (кажущаяся) скорость.
– фазовая (кажущаяся) скорость.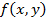 – функция двух действительных переменных, определенная на всей плоскости и достаточно быстро убывающая на бесконечности. Тогда преобразованием Радона функции
– функция двух действительных переменных, определенная на всей плоскости и достаточно быстро убывающая на бесконечности. Тогда преобразованием Радона функции 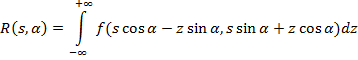
 и проходящей на расстоянии
и проходящей на расстоянии 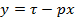 . Тогда преобразование Радона выглядит:
. Тогда преобразование Радона выглядит: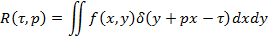
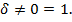
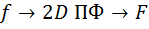
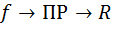
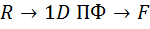
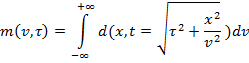
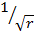 ;
;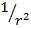 ;
;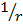 ;
;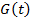 , пропорциональный
, пропорциональный 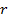 :
: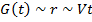 (для среды с постоянной скоростью)
(для среды с постоянной скоростью)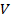 должна использоваться среднеквадратичная скорость
должна использоваться среднеквадратичная скорость 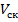 :
: