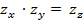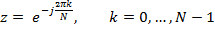Автокорреляционная функция – это частный случай взаимно-корреляционной. Она измеряет степень подобия между временным рядом и его сдвинутой по времени копией как функцию от величины этого сдвига.
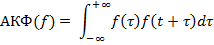
Свойства АКФ:
- максимум функции в нуле (нулевой сдвиг);
- функция симметрична относительно нуля;
- если функция периодична, то АКФ функции периодична с тем же периодом Т.
АКФ и ВКФ нормируются, т.е. делятся на максимальное значение. Таким образом,
maxАКФ = 1.
Свертка в матричном виде
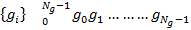

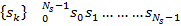
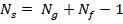
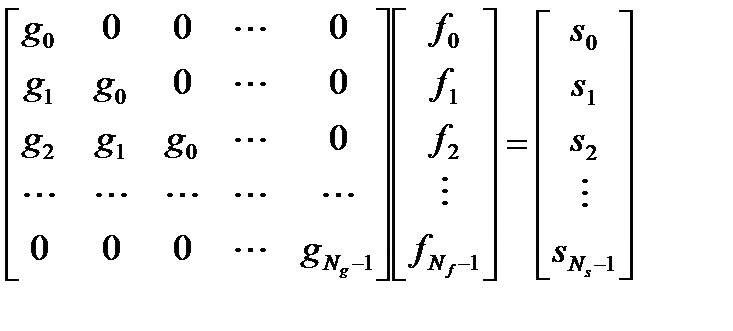
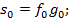

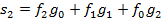
Преобразование Фурье
Преобразование Фурье выступает в трех общих формах, соответствующих трем классам функций:
1. Непрерывные периодические функции. Такие функции повторяются с некоторым периодом  . В этом случае функция представляется как дискретная бесконечная сумма, а коэффициенты Фурье выражаются через интегралы.
. В этом случае функция представляется как дискретная бесконечная сумма, а коэффициенты Фурье выражаются через интегралы.
2. Непрерывные непериодические функции. В этом случае и функция, и коэффициенты Фурье представляются интегралами.
3. Дискретные периодические и непериодические функции. В этом случае функция и коэффициенты Фурье представляются дискретными суммами.
Основной результат Фурье состоит в следующем. Пусть  –периодическая функция времени
–периодическая функция времени 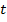 с периодом
с периодом  . Тогда
. Тогда 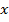 можно представить в виде бесконечного тригонометрического ряда.
можно представить в виде бесконечного тригонометрического ряда.
Свойства преобразования Фурье:
1) Линейность (следует из линейности интеграла):
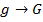
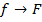
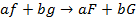
2) Запаздывание: 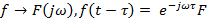
1. Преобразование Фурье для непрерывной периодической функции представляется в виде бесконечной суммы составляющих, а коэффициенты Фурье выражаются через интегралы:
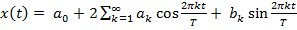 ;
;
Коэффициенты Фурье:
 ,
,
 ,
, 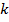 – номер гармоники.
– номер гармоники.
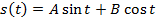
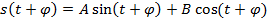
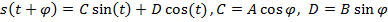 ,
, 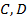 не зависят от
не зависят от 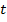
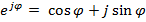
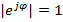 ,
, 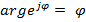
Преобразование Фурье в комплексном виде
Функция представляется в виде дискретной бесконечной суммы составляющих:
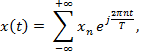
где 
2. Если функция непрерывная непериодическая, то и функция, и коэффициенты Фурье представляются интегралами:
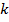 -eкоэффициенты
-eкоэффициенты 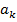 и
и 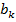 соответствуют стандартно определенной циклической частоте:
соответствуют стандартно определенной циклической частоте:
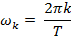
и расстояние между соседними суммируемыми частотными компонентами (разница двух гармоник) составляет:

при 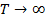 ,
, 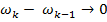
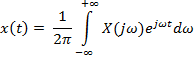
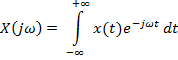
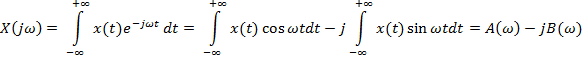
Амплитудный спектр = 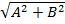
Фазовый спектр = 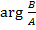 (изменяется в пределах от
(изменяется в пределах от 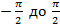 )
)
3. Дискретное преобразование Фурье (ДПФ)
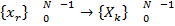
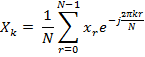
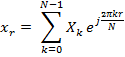
Свойства ДПФ
Периодичность: ДПФ периодично с периодом 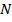 .
.

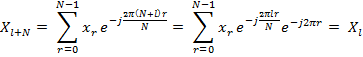
Вещественные временные ряды
Комплексное сопряжение: 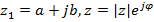 ,
,
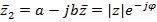
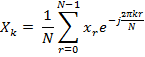
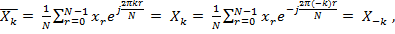 если
если 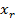 действительное.
действительное.
Таким образом, 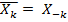
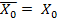 , т.е. компонента нулевой частоты (постоянная составляющая) вещественна и, поскольку вследствие периодичности
, т.е. компонента нулевой частоты (постоянная составляющая) вещественна и, поскольку вследствие периодичности 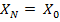 ,
, 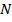 -я частотная компонента также вещественна.
-я частотная компонента также вещественна.
Из свойств сопряжения и периодичности получаем:
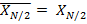 , т.е. компонента с номером
, т.е. компонента с номером 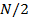 тоже имеет вещественное значение.
тоже имеет вещественное значение.
Используя вышеприведенные свойства, получаем симметрию спектра:
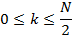
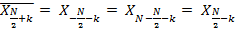
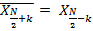
Каждой компоненте соответствует определенная частота. Компоненте с номером 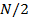 соответствует так называемая частота Найквиста.
соответствует так называемая частота Найквиста.
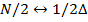
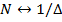 , где
, где  - шаг дискретизации
- шаг дискретизации
Теорема о свертке:
Пусть 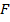 и
и 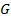 – дискретные преобразования Фурье последовательностей
– дискретные преобразования Фурье последовательностей 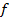 и
и 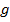 соответственно. Тогда:
соответственно. Тогда:
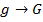 ,
, 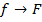
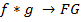
Т. е., свертка во временной области эквивалентна умножению соответствующих преобразований Фурье в частотной области.
Теорема о сдвиге:
По определению ДПФ:
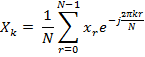
для 


Разбивая сумму на две части, от  до
до 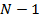 и от
и от 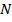 до
до 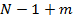 , и учитывая равенство
, и учитывая равенство
 , то получаем
, то получаем 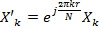 .
.
Интерполяция на основе преобразования Фурье:
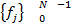 →преобразование Фурье→
→преобразование Фурье→ 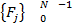 →берем половину спектра→
→берем половину спектра→ 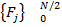 →
→
→делаем линейную интерполяцию→ 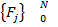 →обратное преобразование Фурье→
→обратное преобразование Фурье→ 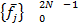
Нуль-фазовый сигнал:
В широком классе свойством минимальной длительности обладает сигнал с нулевым фазовым спектром. Такой сигнал симметричен относительно нулевого момента времени и, следовательно, не обладает свойством причинности. В идеальном случае он может продолжаться до бесконечности в обе стороны от нулевого момента времени.
Быстрое преобразование Фурье
Как следует из самого названия, БПФ – это просто изящный способ быстрого вычисления дискретного преобразования Фурье. Обычный алгоритм ДПФ требует для своего выполнения порядка 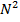 арифметических операций, тогда как при БПФ их требуется только
арифметических операций, тогда как при БПФ их требуется только 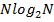 . При типичной для сейсморазведки значении
. При типичной для сейсморазведки значении 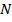 , равном 4096 отсчетов, БПФ вычисляется в 340 раз быстрее ДПФ.
, равном 4096 отсчетов, БПФ вычисляется в 340 раз быстрее ДПФ.

Количество точек во временной последовательности должно равняться степени двойки, для чего на практике последовательность обычно дополняют нулями.
z -преобразование
Рассмотрим временную последовательность с постоянным шагом дискретизации:
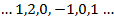
и построим следующий полином от  :
:
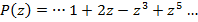
Этот полином и называется -преобразованием.
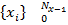
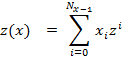
Свойство -преобразования:
если 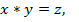 то
то 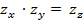
Таким образом, перемножение -преобразований эквивалентно свертке двух исходных последовательностей. Но, согласно теореме о свертке, этой операции эквивалентно и перемножение преобразований Фурье. Следовательно, преобразование Фурье временной последовательности можно рассматривать как частный случай -преобразования, когда
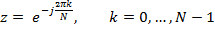



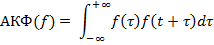
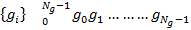

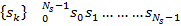
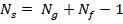
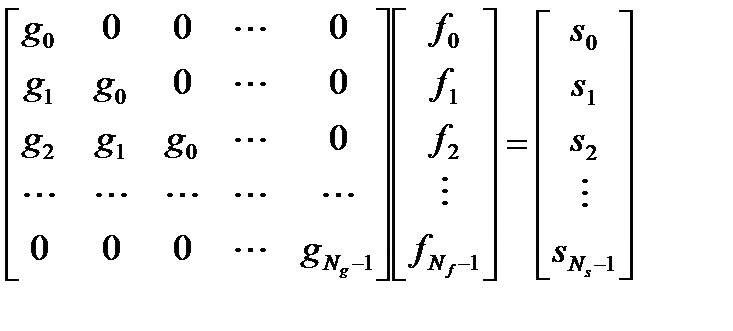
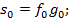

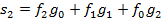
 . В этом случае функция представляется как дискретная бесконечная сумма, а коэффициенты Фурье выражаются через интегралы.
. В этом случае функция представляется как дискретная бесконечная сумма, а коэффициенты Фурье выражаются через интегралы. –периодическая функция времени
–периодическая функция времени 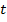 с периодом
с периодом 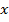 можно представить в виде бесконечного тригонометрического ряда.
можно представить в виде бесконечного тригонометрического ряда.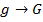
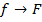
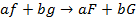
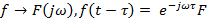
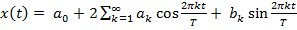 ;
; ,
, ,
, 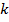 – номер гармоники.
– номер гармоники.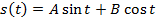
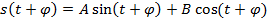
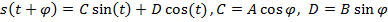 ,
, 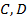 не зависят от
не зависят от 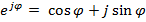
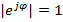 ,
, 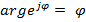
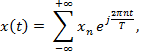

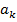 и
и 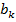 соответствуют стандартно определенной циклической частоте:
соответствуют стандартно определенной циклической частоте: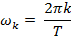

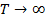 ,
, 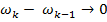
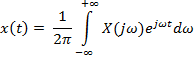
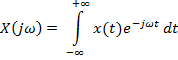
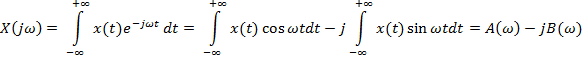
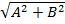
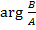 (изменяется в пределах от
(изменяется в пределах от 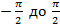 )
)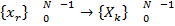
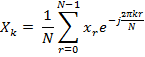
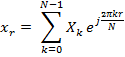
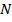 .
.
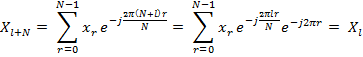
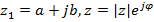 ,
,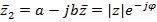
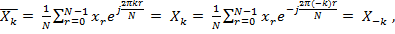 если
если 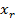 действительное.
действительное.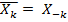
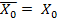 , т.е. компонента нулевой частоты (постоянная составляющая) вещественна и, поскольку вследствие периодичности
, т.е. компонента нулевой частоты (постоянная составляющая) вещественна и, поскольку вследствие периодичности 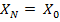 ,
, 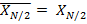 , т.е. компонента с номером
, т.е. компонента с номером 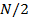 тоже имеет вещественное значение.
тоже имеет вещественное значение.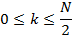
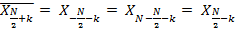
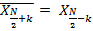
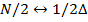
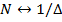 , где
, где  - шаг дискретизации
- шаг дискретизации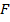 и
и 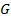 – дискретные преобразования Фурье последовательностей
– дискретные преобразования Фурье последовательностей 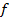 и
и 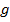 соответственно. Тогда:
соответственно. Тогда: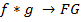



 до
до 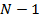 и от
и от 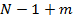 , и учитывая равенство
, и учитывая равенство , то получаем
, то получаем 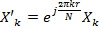 .
.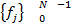 →преобразование Фурье→
→преобразование Фурье→ 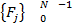 →берем половину спектра→
→берем половину спектра→ 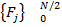 →
→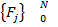 →обратное преобразование Фурье→
→обратное преобразование Фурье→ 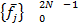
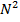 арифметических операций, тогда как при БПФ их требуется только
арифметических операций, тогда как при БПФ их требуется только 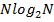 . При типичной для сейсморазведки значении
. При типичной для сейсморазведки значении 
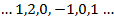
 :
: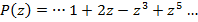
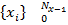
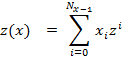
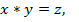 то
то