Суммой двух событий 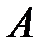 и
и 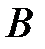 называется событие
называется событие 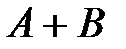 , которое состоит в появлении хотя бы одного из этих событий.
, которое состоит в появлении хотя бы одного из этих событий.
Пример 1. Если 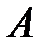 – «при бросании игрального кубика выпало 5 очков»,
– «при бросании игрального кубика выпало 5 очков», 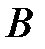 – «при бросании игрального кубика выпало 6 очков», то
– «при бросании игрального кубика выпало 6 очков», то 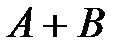 – «при бросании игрального кубика выпало больше 4 очков».
– «при бросании игрального кубика выпало больше 4 очков».
Пример 2. Монета брошена два раза. Если 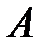 – «появился герб при первом бросании»,
– «появился герб при первом бросании», 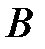 – «появился герб при втором бросании», то
– «появился герб при втором бросании», то 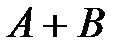 – «герб появился хотя бы один раз».
– «герб появился хотя бы один раз».
Произведением двух событий 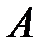 и
и 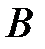 называется событие
называется событие 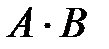 , которое состоит в совместном появлении этих событий.
, которое состоит в совместном появлении этих событий.
Пример 3. Если 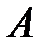 – «при бросании игрального кубика выпало больше 4 очков»,
– «при бросании игрального кубика выпало больше 4 очков», 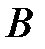 – «при бросании игрального кубика выпало четное число очков», то
– «при бросании игрального кубика выпало четное число очков», то 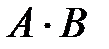 – «при бросании игрального кубика выпало 6 очков».
– «при бросании игрального кубика выпало 6 очков».
Пример 4. Если 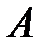 – «в подъезд вошел мужчина»,
– «в подъезд вошел мужчина», 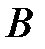 – «в подъезд вошел светловолосый человек», то
– «в подъезд вошел светловолосый человек», то 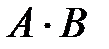 – «в подъезд вошел светловолосый мужчина».
– «в подъезд вошел светловолосый мужчина».
Аналогично можно определить сумму и произведение любого конечного числа событий.
События 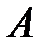 и
и 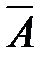 называются противоположными, если они несовместны и образуют полную группу событий.
называются противоположными, если они несовместны и образуют полную группу событий.
Пример 5. События 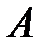 – «при бросании игрального кубика выпало четное число очков» и
– «при бросании игрального кубика выпало четное число очков» и 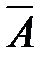 – «при бросании игрального кубика выпало нечетное число очков» являются противоположными.
– «при бросании игрального кубика выпало нечетное число очков» являются противоположными.
Пример 6. Стрелок стреляет по мишени один раз. События 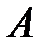 – «стрелок попал в мишень» и
– «стрелок попал в мишень» и 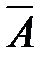 – «стрелок промахнулся» являются противоположными.
– «стрелок промахнулся» являются противоположными.
Теорема сложения вероятностей.
Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления:
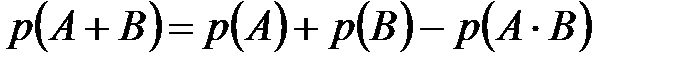 .
.
В частности, если события 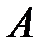 и
и 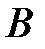 несовместны, то
несовместны, то
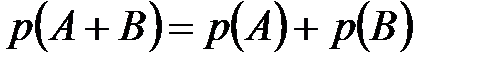 .
.
Теорема сложения вероятностей справедлива для любого конечного числа несовместных событий.
Если события 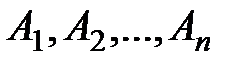 несовместны, то
несовместны, то
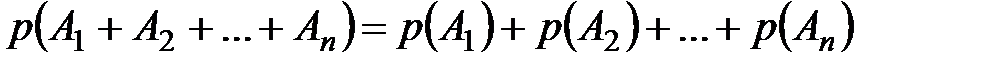 .
.
Следствия теоремы сложения вероятностей:
1. Сумма вероятностей несовместных событий 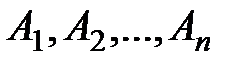 , образующих полную группу, равна 1.
, образующих полную группу, равна 1.
2. Сумма вероятностей противоположных событий равна 1, то есть 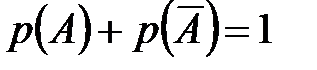 .
.
Условной вероятностью 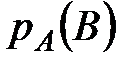 называется вероятность события
называется вероятность события 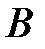 , вычисленная в предположении, что событие
, вычисленная в предположении, что событие 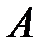 уже наступило.
уже наступило.
Два события называются независимыми, если появление любого из них не изменяет вероятности появления другого, то есть
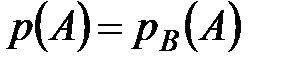 или
или 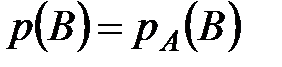 .
.
Несколько событий называются независимыми в совокупности (независимыми), если они попарно независимы и независимы каждое из них и все возможные произведения остальных.
Теорема умножения вероятностей.
Вероятность произведения двух событий 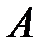 и
и 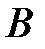 находится по формуле:
находится по формуле:
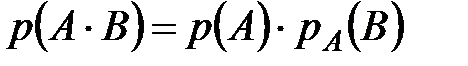 .
.
В частности, если события 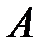 и
и 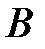 независимы, то
независимы, то
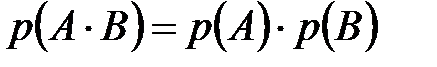 .
.
Теорема умножения вероятностей справедлива для любого конечного числа событий:
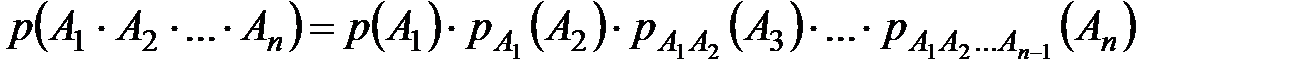 , где
, где
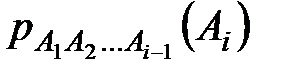 – вероятность события
– вероятность события 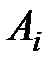 , вычисленная в предположении, что события
, вычисленная в предположении, что события 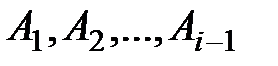 уже наступили.
уже наступили.
В частности, если события 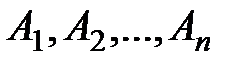 независимы, то
независимы, то
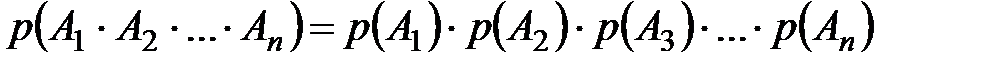 .
.
Пример 7. В урне 4 белых и 7 черных шаров. Наудачу по одному извлекают два шара без возвращения. Найти вероятность того, что оба шара окажутся белыми.
Рассмотрим события:
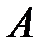 – «первый шар оказался белым»;
– «первый шар оказался белым»;
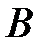 – «второй шар оказался белым»;
– «второй шар оказался белым»;
 – «оба шара оказались белыми».
– «оба шара оказались белыми».
По определения произведения событий заключаем, что 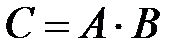 .
.
Тогда по теореме умножения вероятностей
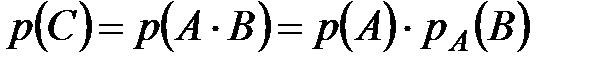 .
.
Вероятность того, что первый шар окажется белым, 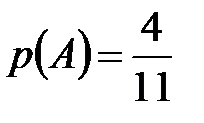 .
.
Вероятность того, что второй шар окажется белым, при условии, что первый шар оказался белым, то есть условная вероятность 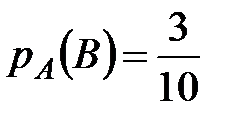 (после того, как из урны извлечен один белый шар, в ней осталось 10 шаров, из них 3 белых).
(после того, как из урны извлечен один белый шар, в ней осталось 10 шаров, из них 3 белых).
Окончательно получаем 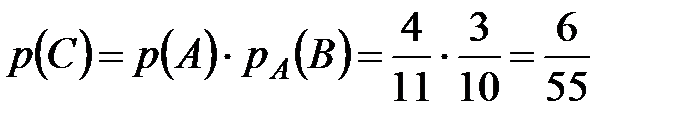 .
.
Пример 8. Брошены два игральных кубика. Найти вероятность того, что на первом кубике выпало четное число очков, а на втором – меньше 5 очков.
Введем обозначения событий:
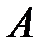 – «на первом кубике выпало четное число очков»;
– «на первом кубике выпало четное число очков»;
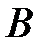 – «на втором кубике выпало меньше 5 очков»;
– «на втором кубике выпало меньше 5 очков»;
 – «на первом кубике выпало четное число очков, а на втором – меньше 5 очков».
– «на первом кубике выпало четное число очков, а на втором – меньше 5 очков».
По определению произведения событий, 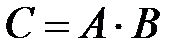 .
.
Из условия задачи следует, что события 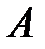 и
и 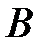 независимы. Очевидно, что
независимы. Очевидно, что 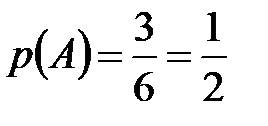 ,
, 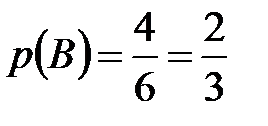 . Тогда по теореме умножения вероятностей для независимых событий находим:
. Тогда по теореме умножения вероятностей для независимых событий находим:
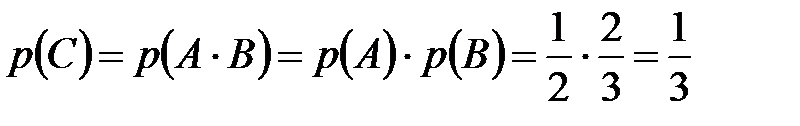 .
.
Пример 9. Вероятность поломки первого станка в течение смены равна 0,15, а второго – 0,08. Считая, что станки работают независимо друг от друга, найти вероятность того, что в течение смены поломается хотя бы один станок.
Пусть 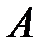 – «поломался первый станок»;
– «поломался первый станок»; 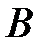 – «поломался второй станок»;
– «поломался второй станок»;  – «поломался хотя бы один станок».
– «поломался хотя бы один станок».
По определению суммы событий, 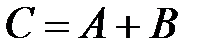 .
.
По теореме сложения вероятностей
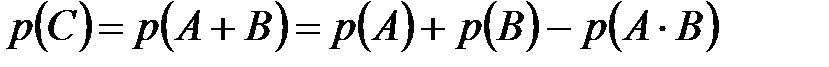 .
.
Станки работают независимо друг от друга, поэтому события 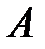 и
и 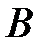 независимы. Значит
независимы. Значит 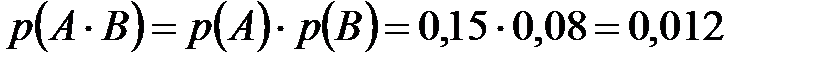 .
.
Тогда искомая вероятность
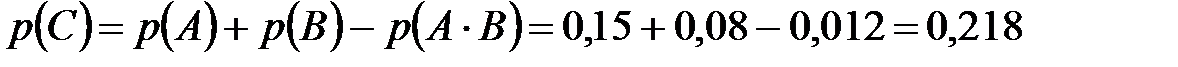 .
.
Пример 10. Стрелок выстрелил три раза по удаляющейся цели. Вероятность попадания в цель при первом выстреле равна 0,8, при втором – 0,7, при третьем – 0,6. Найти вероятность того, что стрелок: а) попадет три раза; б) промахнется три раза; в) попадет ровно один раз; г) попадет ровно два раза; д) попадет хотя бы один раз.
Рассмотрим события:
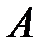 – «стрелок попал в цель при первом выстреле»;
– «стрелок попал в цель при первом выстреле»;
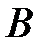 – «стрелок попал в цель при втором выстреле»;
– «стрелок попал в цель при втором выстреле»;
 – «стрелок попал в цель при третьем выстреле».
– «стрелок попал в цель при третьем выстреле».
По условию задачи, 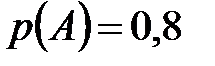 ,
, 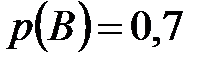 ,
, 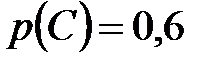 .
.
Рассмотрим противоположные события:
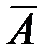 – «стрелок промахнулся при первом выстреле»;
– «стрелок промахнулся при первом выстреле»;
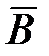 – «стрелок промахнулся при втором выстреле»;
– «стрелок промахнулся при втором выстреле»;
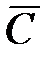 – «стрелок промахнулся при третьем выстреле».
– «стрелок промахнулся при третьем выстреле».
По следствию из теоремы сложения вероятностей, найдем:
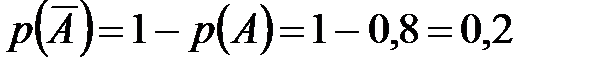 ;
; 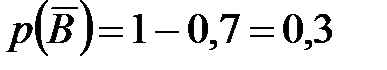 ;
; 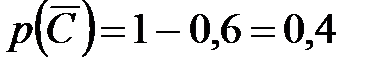 .
.
а) Найдем вероятность события 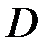 – «стрелок попал в цель три раза». Очевидно, что
– «стрелок попал в цель три раза». Очевидно, что 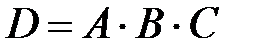 .
.
Так как, по условию задачи, вероятность попадания в цель при каждом выстреле не зависит от результата предыдущих выстрелов, то события 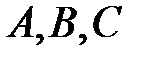 являются независимыми. Значит, по теореме умножения вероятностей
являются независимыми. Значит, по теореме умножения вероятностей
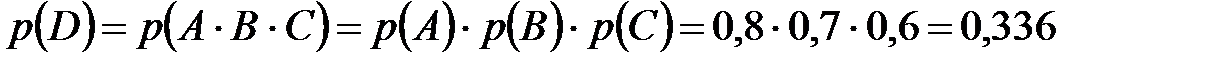 .
.
б) Найдем вероятность события 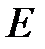 – «стрелок промахнулся три раза». Поскольку
– «стрелок промахнулся три раза». Поскольку 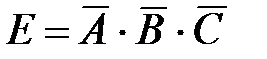 и события
и события 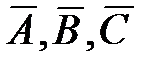 независимы, то
независимы, то
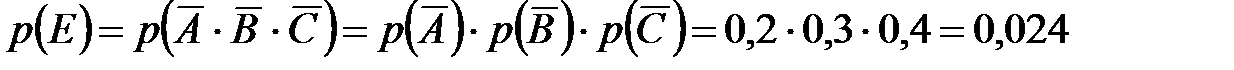 .
.
в) Вычислим вероятность события 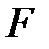 – «стрелок попал в цель ровно один раз». Событие
– «стрелок попал в цель ровно один раз». Событие 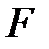 является суммой трех событий: стрелок может попасть в цель при первом выстреле и при этом промахнуться при втором и третьем выстрелах; может попасть в цель при втором выстреле и при этом промахнуться при первом и третьем выстрелах; наконец, он может попасть в цель при третьем выстреле и при этом промахнуться при первом и втором выстрелах, то есть
является суммой трех событий: стрелок может попасть в цель при первом выстреле и при этом промахнуться при втором и третьем выстрелах; может попасть в цель при втором выстреле и при этом промахнуться при первом и третьем выстрелах; наконец, он может попасть в цель при третьем выстреле и при этом промахнуться при первом и втором выстрелах, то есть
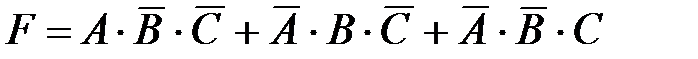 .
.
Слагаемые, стоящие в правой части последнего равенства, несовместны, а сомножители в каждом слагаемом независимы. Тогда, по теоремам сложения и умножения вероятностей
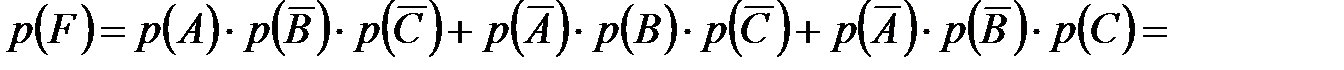
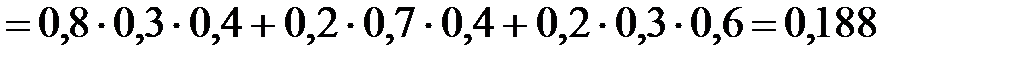 .
.
г) Событие 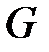 – «стрелок попал в цель ровно два раза» выражается через события
– «стрелок попал в цель ровно два раза» выражается через события 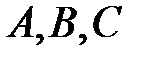 следующим образом:
следующим образом:
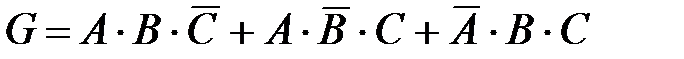 .
.
Значит, 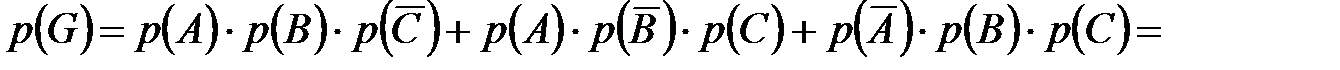
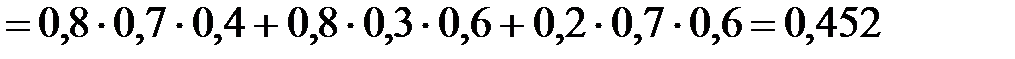 .
.
д) Рассмотрим событие 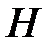 – «стрелок попал в цель хотя бы один раз». Событие
– «стрелок попал в цель хотя бы один раз». Событие 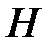 является суммой событий
является суммой событий 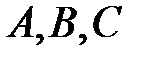 . Однако события
. Однако события 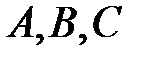 являются совместными, и вероятность их суммы не равна сумме их вероятностей. В данном случае удобно рассмотреть противоположное событие
являются совместными, и вероятность их суммы не равна сумме их вероятностей. В данном случае удобно рассмотреть противоположное событие 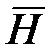 – «стрелок не попал в цель ни разу».
– «стрелок не попал в цель ни разу».
Заметим, что 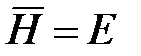 . Следовательно,
. Следовательно,
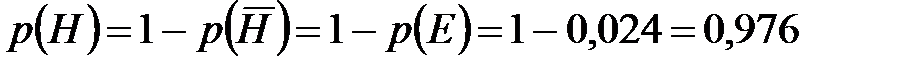 .
.
Пример 11. Студент решил правильно 6 из 10 заданных задач. Найти вероятность того, что из трех случайной выбранных преподавателем для проверки задач правильно решены две.
Введем обозначения событий: 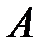 – «первая из выбранных для проверки задач решена правильно»;
– «первая из выбранных для проверки задач решена правильно»; 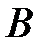 – «вторая задача решена правильно»;
– «вторая задача решена правильно»;  – «третья задача решена правильно»;
– «третья задача решена правильно»; 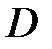 – «правильно решены две задачи».
– «правильно решены две задачи».
Выразим событие 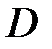 через события
через события 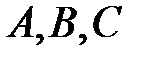 :
:
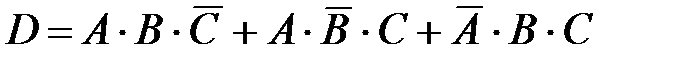 .
.
Слагаемые, стоящие в правой части равенства, несовместны, однако сомножители в каждом слагаемом зависимы (так как вероятность того, что очередная выбранная преподавателем для проверки задача решена правильно, зависит от того, правильно ли были решены предыдущие задачи). Следовательно, по теоремам сложения и умножения вероятностей
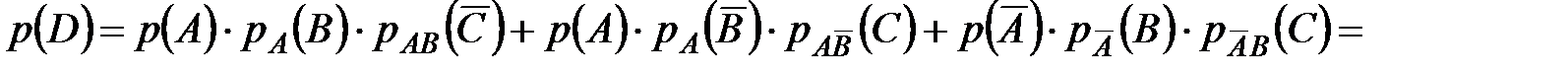
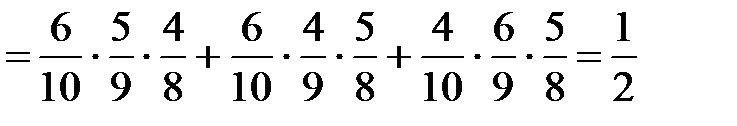 .
.
Задачи
1. Брошены две монеты. Найти вероятность того, что выпадет хотя бы один герб.
2. В урне 5 красных и 8 белых шаров. Из урны последовательно без возвращения вынимают два шара. Найти вероятность того, что: а) оба шара белые; б) оба шара красные; в) первый шар белый, а второй красный; г) шары разного цвета.
3. Имеются 2 изделия первого сорта, 4 изделия второго сорта и 5 изделий третьего сорта. Случайным образом отбирается одно изделие. Найти вероятность того, что оно: а) первого или второго сорта; б) не второго сорта.
4. Брошены четыре монеты.Какова вероятность того, что на всех четырех монетах выпадет герб?
5. В лотерее выпущено 10000 билетов и установлены 10 выигрышей по 1000 рублей, 100 – по 500 рублей, 500 – по 100 рублей и 1000 выигрышей по 25 рублей. Гражданин купил 1 билет. Какова вероятность того, что он выиграет не меньше 100 рублей?
6. Игральный кубик брошен два раза. Найти вероятность того, что хотя бы один раз выпадет: а) 4 очка; б) меньше 3 очков.
7. Брошены три игральных кубика. Найти вероятность того, что: а) на всех кубиках выпало нечетное число очков; б) на первом кубике выпало 1 очко, на втором – 2 очка, на третьем – 3 очка; в) на первом кубике выпало 6 очков, на втором – больше 2 очков, на третьем – не больше 5 очков.
8. Рабочий обслуживает 5 станков. 20% времени он уделяет первому станку, 10% – второму, 15% – третьему, 25% – четвертому и 30% пятому станку. Какова вероятность того, что случайно заглянувший в цех мастер найдет рабочего: а) у первого или третьего станка; б) у первого или пятого станка; в) у первого или у второго или у третьего станка?
9. Из колоды в 36 карт одну за другой (без возвращения) вытаскивают 2 карты. Какова вероятность того, что появятся: а) 2 дамы; б) ни одной дамы; в) хотя бы одна дама; г) валет и дама?
10. В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны три человека. Найти вероятность того, что все отобранные лица окажутся: а) мужчинами; б) женщинами; в) лицами одного пола.
11. В ящике 10 деталей, среди которых 6 окрашенных. Сборщик наудачу извлекает 4 детали. Найти вероятность того, что все извлеченные детали окажутся: а) окрашенными; б) неокрашенными.
12. Деталь проходит три независимых операции обработки. Вероятность получения брака на первой операции равна 0,02, на второй – 0,03, на третьей – 0,01. Найти вероятность получения детали без брака после трех операций.
13. Из цифр 1, 2, 3, 4, 5 выбирается одна цифра, а из оставшихся цифр – вторая. Найти вероятность того, что выбраны две нечетные цифры.
14. Два стрелка сделали по одному выстрелу по мишени. Вероятность попадания в мишень для первого стрелка равна 0,6, а для второго – 0,7. Найти вероятности следующих событий: а) только один из стрелков попадет в мишень; б) оба стрелка попадут в мишень; в) ни один из стрелков не попадет в мишень; г) хотя бы один из стрелков попадет в мишень; д) хотя бы один стрелок промахнется.
15. Студент знает ответы на 20 вопросов из 25. Экзаменатор последовательно задает студенту три вопроса. Найти вероятность того, что студент: а) ответит на все вопросы; б) не ответит ни на один вопрос; в) ответит на первый и второй вопросы, но не ответит на третий вопрос; г) ответит только на один вопрос.
16. Монета брошена три раза. Найти вероятность того, что цифра выпадет: а) ровно один раз; б) ровно два раза; в) хотя бы один раз.
17. Из полной колоды карт (52 карты) вынимается одна карта. Даны события: А – «появление туза»; В – «появление карты красной масти»; С – «появление бубнового туза»; D – «появление десятки». Найти безусловные и условные вероятности в каждой из указанных пар событий и определить, зависимы или независимы эти события: а) А и В; б) А и С; в) В и С; г) В и D.
18. Студент должен сдать в сессию экзамены по истории, иностранному языку и экономике. Вероятность того, что студент сдаст экзамен по истории, равна 0,75, по иностранному языку – 0,9, по экономике – 0,5. Найти вероятность того, что студент: а) сдаст все экзамены; б) не сдаст ни одного экзамена; в) сдаст один экзамен; г) сдаст хотя бы один экзамен.
19. Четыре исследователя, независимо друг от друга, производят измерение некоторой физической величины. Вероятность того, что исследователь допустит ошибку при считывании показаний прибора, равна 0,1. Найти вероятность того, что при однократном измерении ошибка будет допущена: а) всеми исследователями; б) хотя бы одним исследователем; в) только двумя исследователями.
20. Вероятность попадания в цель при одном выстреле для первого стрелка равна p, для второго – 0,7. Вероятность ровно одного попадания при одном выстреле обоих стрелков равна 0,38. Найти p.
21. Между двумя городами в течение суток осуществляется четыре авиарейса: утренний, дневной, вечерний и ночной. В среднем задерживаются 15% утренних, 20% вечерних, 10% дневных и ночных рейсов. Найти вероятность того, что в течение наступающих суток: а) будут задержаны все четыре авиарейса; б) не будет задержан ни один авиарейс; в) будет задержан хотя бы один авиарейс; г) будут задержаны три авиарейса; д) будут задержаны два авиарейса.
22. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,6, а для второго – p. Вероятность того, что при одном выстреле обоих стрелков произойдет хотя бы одно попадание, равна 0,9. Найти p.
23. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,6; 0,7.
24. Вероятность хотя бы одного попадания в цель при четырех независимых выстрелах равна 0,9984. а) Найти вероятность попадания в цель при одном выстреле. б) Найти вероятность того, что при трех выстрелах произойдет ровно два попадания в цель.
25. В мешке содержится десять одинаковых кубиков с номерами от 1 до 10. Наудачу извлекают по одному три кубика. Найти вероятность того, что последовательно появятся кубики с номерами 1, 2, 3, если кубики извлекаются: а) без возвращения; б) с возвращением (извлеченный кубик возвращается в мешок).
26. В урнах находятся шары, отличающиеся только цветом. В первой урне – 4 белых, 10 черных и 7 красных шаров, во второй - 9 белых, 7 черных и 5 красных шаров. Из обеих урн наудачу извлекли по одному шару. Какова вероятность того, что оба шара одного цвета?
Ответы
1. 0,75. 2. а) 14/39;б) 5/39;в) 10/39;г) 20/39. 3. а) 6/11; б) 7/11. 4. 1/16. 5. 0,061. 6. а) 11/36;б) 5/9. 7. а) 1/8; б) 1/216; в) 5/54. 8. а) 0,35; б) 0,5; в) 0,45. 9. а) 1/105; б) 248/315; в) 67/315; г) 8/315. 10. а) 7/24; б) 1/120; в) 3/10. 11. а) 1/14;б) 1/210. 12. 0,94. 13. 0,3. 14. а) 0,46; б) 0,42; в) 0,12; г) 0,88; д) 0,58. 15. а) 57/115; б) 1/230; в) 19/138; г) 2/23. 16. а) 3/8;б) 3/8;в) 3/4. 17. а) независимы; б) зависимы; в) зависимы; г) независимы. 18. а) 0,3375; б) 0,0125; в) 0,1625; г) 0,9875. 19. а) 0,0001; б) 0,3439; в) 0,0486. 20. 0,8. 21. а) 0,0003; б) 0,5508; в) 0,4492; г) 0,0083; д) 0,0833. 22. 0,75. 23. 0,9496. 24. а) 0,8; б) 0,384. 25. а) 1/720; б) 1/1000. 26. 47/147.



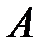 и
и 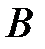 называется событие
называется событие 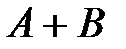 , которое состоит в появлении хотя бы одного из этих событий.
, которое состоит в появлении хотя бы одного из этих событий.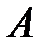 – «при бросании игрального кубика выпало 5 очков»,
– «при бросании игрального кубика выпало 5 очков», 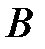 – «при бросании игрального кубика выпало 6 очков», то
– «при бросании игрального кубика выпало 6 очков», то 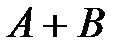 – «при бросании игрального кубика выпало больше 4 очков».
– «при бросании игрального кубика выпало больше 4 очков».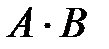 , которое состоит в совместном появлении этих событий.
, которое состоит в совместном появлении этих событий.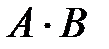 – «при бросании игрального кубика выпало 6 очков».
– «при бросании игрального кубика выпало 6 очков».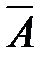 называются противоположными, если они несовместны и образуют полную группу событий.
называются противоположными, если они несовместны и образуют полную группу событий.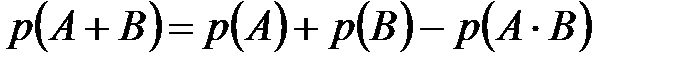 .
.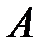 и
и 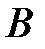 несовместны, то
несовместны, то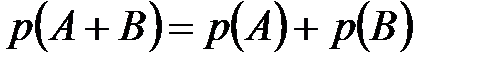 .
.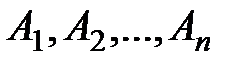 несовместны, то
несовместны, то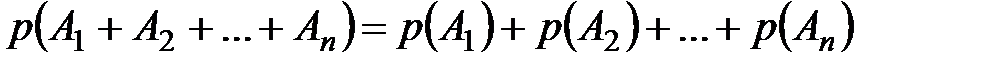 .
.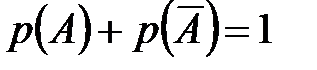 .
.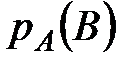 называется вероятность события
называется вероятность события 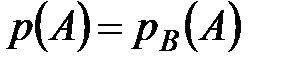 или
или 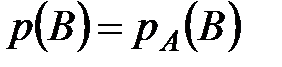 .
.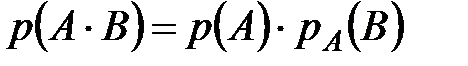 .
.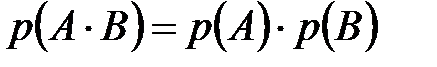 .
.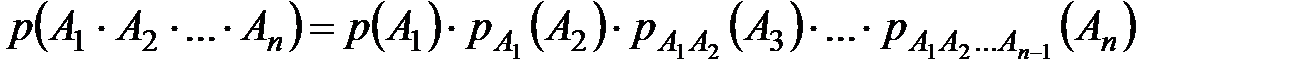 , где
, где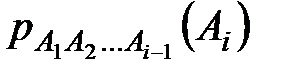 – вероятность события
– вероятность события 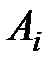 , вычисленная в предположении, что события
, вычисленная в предположении, что события 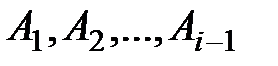 уже наступили.
уже наступили.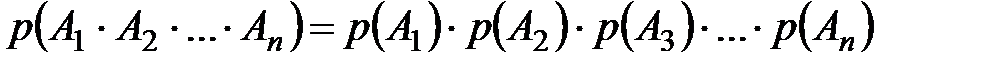 .
.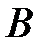 – «второй шар оказался белым»;
– «второй шар оказался белым»; – «оба шара оказались белыми».
– «оба шара оказались белыми».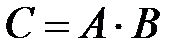 .
.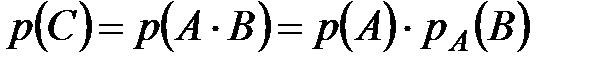 .
.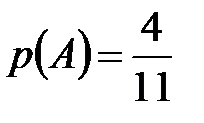 .
.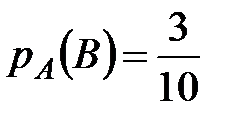 (после того, как из урны извлечен один белый шар, в ней осталось 10 шаров, из них 3 белых).
(после того, как из урны извлечен один белый шар, в ней осталось 10 шаров, из них 3 белых).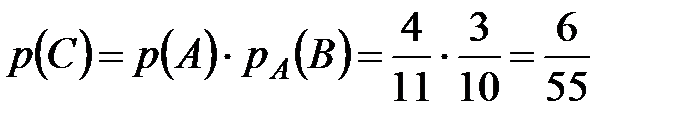 .
.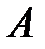 и
и 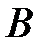 независимы. Очевидно, что
независимы. Очевидно, что 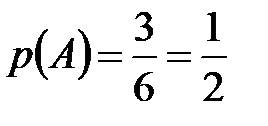 ,
, 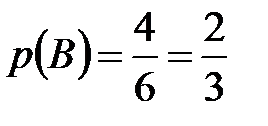 . Тогда по теореме умножения вероятностей для независимых событий находим:
. Тогда по теореме умножения вероятностей для независимых событий находим: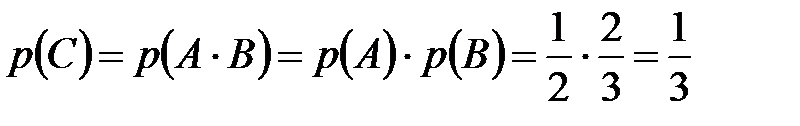 .
.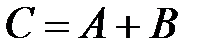 .
.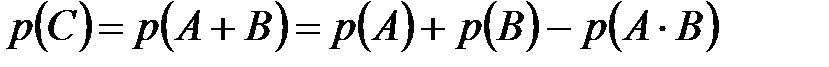 .
.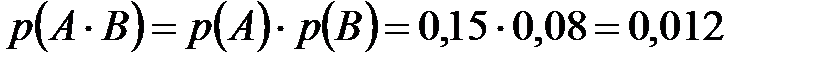 .
.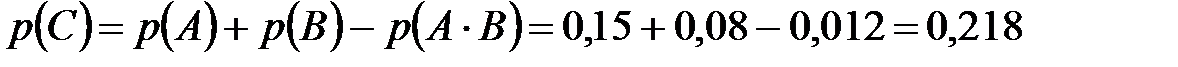 .
.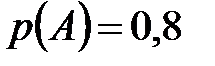 ,
, 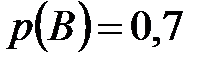 ,
, 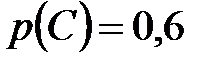 .
.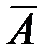 – «стрелок промахнулся при первом выстреле»;
– «стрелок промахнулся при первом выстреле»;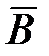 – «стрелок промахнулся при втором выстреле»;
– «стрелок промахнулся при втором выстреле»;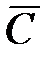 – «стрелок промахнулся при третьем выстреле».
– «стрелок промахнулся при третьем выстреле».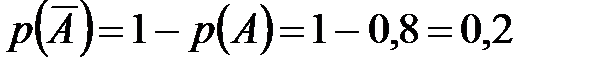 ;
; 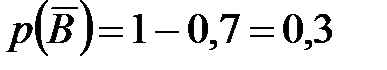 ;
; 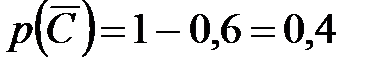 .
.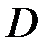 – «стрелок попал в цель три раза». Очевидно, что
– «стрелок попал в цель три раза». Очевидно, что 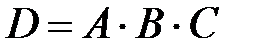 .
.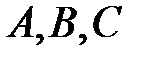 являются независимыми. Значит, по теореме умножения вероятностей
являются независимыми. Значит, по теореме умножения вероятностей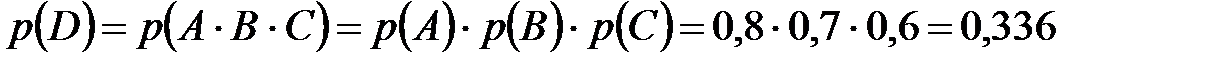 .
.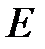 – «стрелок промахнулся три раза». Поскольку
– «стрелок промахнулся три раза». Поскольку 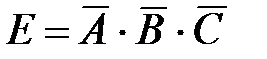 и события
и события 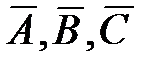 независимы, то
независимы, то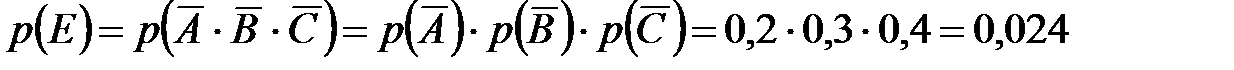 .
.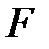 – «стрелок попал в цель ровно один раз». Событие
– «стрелок попал в цель ровно один раз». Событие 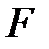 является суммой трех событий: стрелок может попасть в цель при первом выстреле и при этом промахнуться при втором и третьем выстрелах; может попасть в цель при втором выстреле и при этом промахнуться при первом и третьем выстрелах; наконец, он может попасть в цель при третьем выстреле и при этом промахнуться при первом и втором выстрелах, то есть
является суммой трех событий: стрелок может попасть в цель при первом выстреле и при этом промахнуться при втором и третьем выстрелах; может попасть в цель при втором выстреле и при этом промахнуться при первом и третьем выстрелах; наконец, он может попасть в цель при третьем выстреле и при этом промахнуться при первом и втором выстрелах, то есть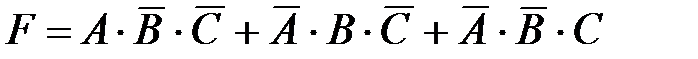 .
.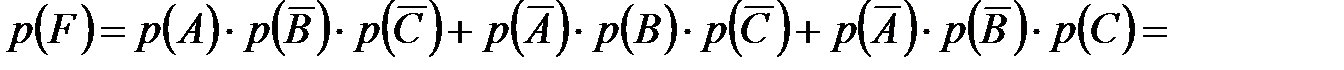
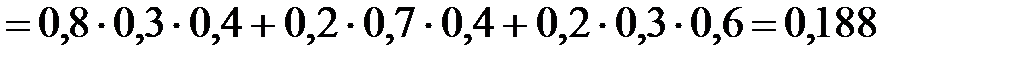 .
. – «стрелок попал в цель ровно два раза» выражается через события
– «стрелок попал в цель ровно два раза» выражается через события 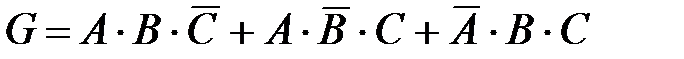 .
.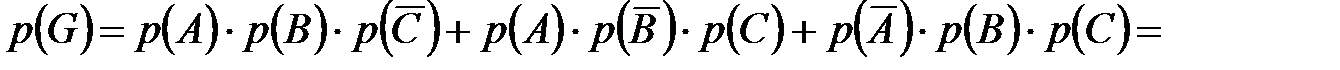
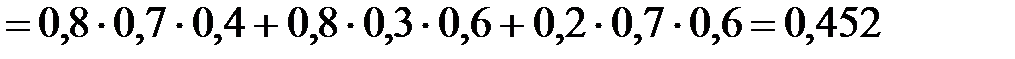 .
.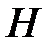 – «стрелок попал в цель хотя бы один раз». Событие
– «стрелок попал в цель хотя бы один раз». Событие 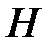 является суммой событий
является суммой событий 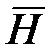 – «стрелок не попал в цель ни разу».
– «стрелок не попал в цель ни разу».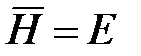 . Следовательно,
. Следовательно,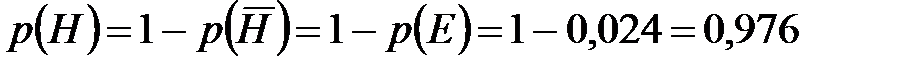 .
.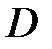 – «правильно решены две задачи».
– «правильно решены две задачи».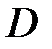 через события
через события 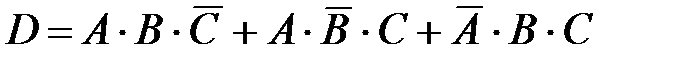 .
.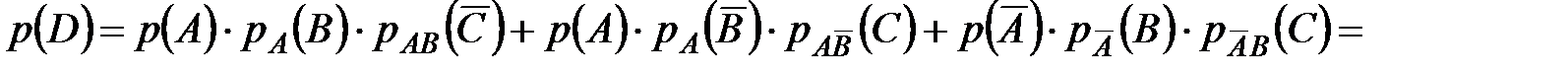
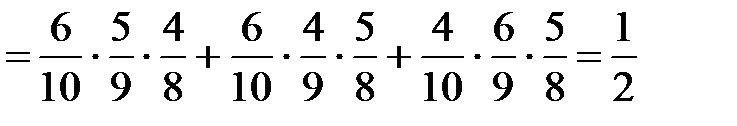 .
.


