

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
5. Радиус-вектор 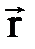 – это вектор, проведённый из начала координат в данную точку.
– это вектор, проведённый из начала координат в данную точку.
Его проекции на координатные оси равны декартовым координатам данной точки. В пространственной декартовой системе координат радиус–вектор 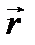 можно представить следующим образом:
можно представить следующим образом:
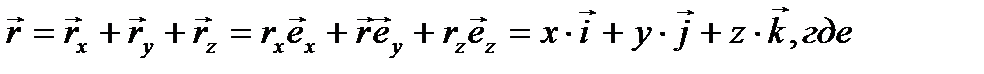
| (2.11) |
rx = x; ry =y; rz =z - проекции вектора 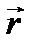 на координатные оси.
на координатные оси.
6. Приращение - это то, что стало, минус то, что было.
Обозначают приращение символом D - дельта.
Пусть первоначальная длина некоторого вектора 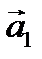 , конечная –
, конечная – 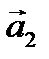 .
.
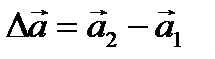 . .
| (2.12) |
Выражение (2.12) определяет приращение вектора 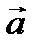 ,а (2.13) приращение скаляра:
,а (2.13) приращение скаляра:
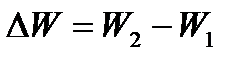
| (2.13) |
Модулем приращения вектора 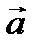 – называется выражение (2.14):
– называется выражение (2.14):
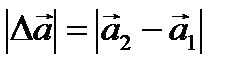 . .
| (2.14) |
Приращением модуля вектора 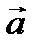 называется выражение (2.15):
называется выражение (2.15):
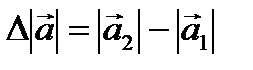 . .
| (2.15) |
7. Скалярное произведение векторов
Скалярным произведением векторов называется скаляр, равный произведению модулей перемножаемых векторов и косинуса угла между ними:
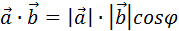
| (2.16) |
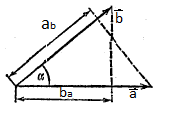
Рис. 2.8. Скалярное произведение векторов
Произведение 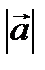 cos α= ab равно проекции вектора
cos α= ab равно проекции вектора 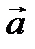 на направление вектора
на направление вектора 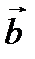 , а произведение
, а произведение  cos α= ba - проекции вектора
cos α= ba - проекции вектора 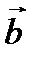 на направление вектора
на направление вектора 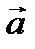 .
.
Из рис.2.8. следует, что:
скалярное произведение модуля одного вектора можно рассматривать как произведение модуля одного из перемножаемых векторов на проекцию другого вектора на направление первого.
Скалярное произведение обладает свойствами коммутативности и дистрибутивности.
Коммутативность означает, что произведение не зависит от порядка сомножителей: 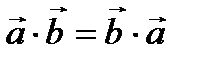 .
.
Дистрибутивность заключается в том, что произведение сумм векторов равно сумме произведений слагаемых, взятых попарно, например:
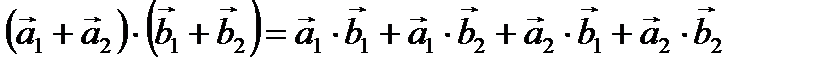 . .
| (2.17) |
Аналогичное равенство имеет место при любом числе слагаемых в каждом сомножителе.
Скалярные произведения ортов координатных осей декартовой системы координат равны:
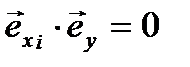 , т.к. , т.к. 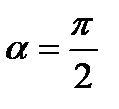 , а , а 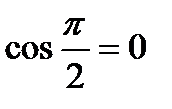 . .
| (2.18) |
Под квадратом модуля понимают скалярное произведение вектора самого на себя:
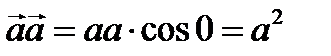 . .
| (2.19) |
Векторное произведение векторов
Векторное произведение векторов 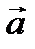 и
и 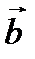 обозначается так:
обозначается так:
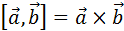
|
Векторным произведением векторов 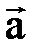 и
и 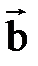 называют вектор
называют вектор 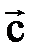 , определяемый соотношением (2.20):
, определяемый соотношением (2.20):
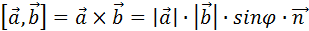
| (2.20) |
где 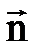 – вектор нормали к плоскости, в которой лежат векторы
– вектор нормали к плоскости, в которой лежат векторы 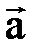 и
и 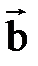 .
.
Направление вектора 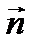 выбирается так, чтобы тройка векторов-
выбирается так, чтобы тройка векторов- 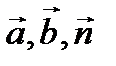 - образовывала правовинтовую систему: если смотреть вдоль вектора
- образовывала правовинтовую систему: если смотреть вдоль вектора 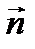 , то поворот по кратчайшему пути от первого сомножителя ко второму осуществляется по часовой стрелке.
, то поворот по кратчайшему пути от первого сомножителя ко второму осуществляется по часовой стрелке.
Модуль векторного произведения определяется соотношением 
|
|
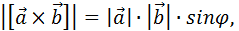
| (2.21) |
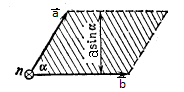
Рис. 2.9. Векторное произведение векторов 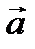 и
и 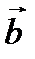
Свойства векторного произведения:
векторное произведение в отличие от скалярного некоммутативно, но обладает свойством дистрибутивности.
1. 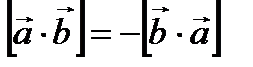 . – векторное произведение векторов некоммутативно; . – векторное произведение векторов некоммутативно;
| (2.22) | ||
| 2. | (2.23) | ||
|
|
|

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!