

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Ускорением называется физическая величина, характеризующая быстроту изменения скорости по модулю и направлению.
Средним ускорением неравномерного движения в интервале от t до t+Dt называется векторная величина, равная отношению приращения вектора скорости - DV к приращению времени - Dt.
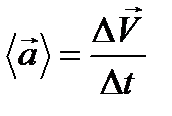
| (5.1) |
Вектор среднего ускорения сонаправлен с вектором приращения вектора скорости: <а>DV.
Модуль вектора среднего ускорения определяется формулой:
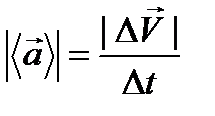
| (5.2) |
Единицей измерения ускорения в системе СИ является - 1 м/c2.
Если Dt®0, то <а>® а мгн
Мгновенным ускорением частицы (МТ) в момент времени t является предел отношения приращения вектора скорости к приращению времени, за которое оно (приращение вектора скорости) произошло:
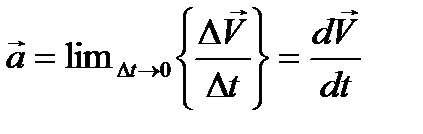
| (5.3) |
Мгновенное ускорение есть первая производная от вектора скорости по времени, или вторая производная радиус - вектора по времени:
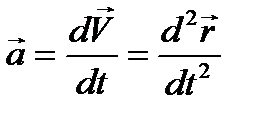
| (5.4) |
Но радиус - вектор 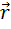 можно представить в виде:
можно представить в виде:
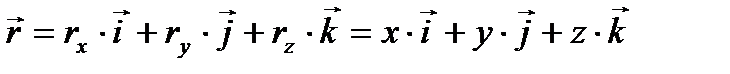
| (5.5) |
и тогда вектор ускорения 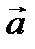 можно представить в виде:
можно представить в виде:
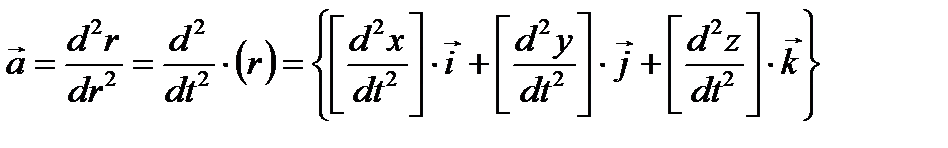
| (5.6) |
Компоненты вектора мгновенного ускорения равны вторым производным соответствующих координат по времени:
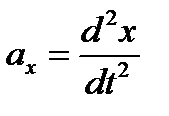 , , 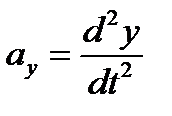 , , 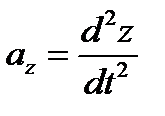
| (5.7) |
В общем случае вектор ускорения можно представить в следующем виде:
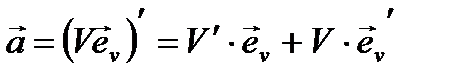
| (5.8) |
Рассмотрим теперь два частных случая: 1) движение по прямолинейной траектории и 2) равномерное движение по окружности.
1. При движении в одну и ту же сторону по прямолинейной траектории скорость изменяется только по модулю. Представим скорость в виде:
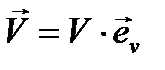
| (5.9) |
где 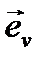 - орт вектора скорости.
- орт вектора скорости.
Рассмотрим движение по прямолинейной траектории:
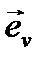 = const, а изменяется только модуль скорости - V.
= const, а изменяется только модуль скорости - V.
Тогда
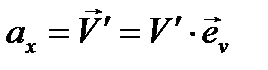
| (5.10) |
Это ускорение называется тангенциальной (касательной) составляющей ускорения и обозначается -  .
.
Если V¢>0, то ускорение 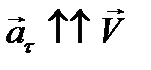 .
.
Если же V¢<0, то 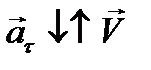 , а | ax |=| V ¢ |.
, а | ax |=| V ¢ |.
Рассмотрим равномерное движение по окружности радиуса R, V=const, а еv - изменяется, тогда:
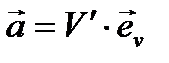
| (5.11) |
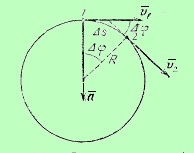
Pис. 5.1. В момент времени t частица находилась в точке 1, а спустя время Dt она оказалась в точке 2, пройдя путь DS= 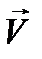 Dt; за этот промежуток времени орт скорости поворачивается на угол Dj и получает приращение
Dt; за этот промежуток времени орт скорости поворачивается на угол Dj и получает приращение 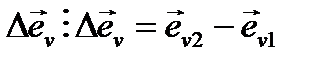
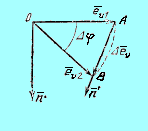
| B |
Приращение угла поворота равно:
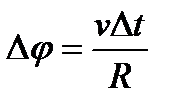
| (5.12) |
По определению производной:
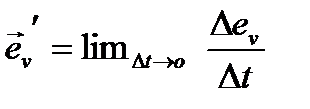
| (5.13) |
Если Dt®0, то Dj®0, а отношение хорды АВ к длине дуги È АВ®1. Тогда приняв 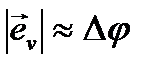 , можно написать что,
, можно написать что, 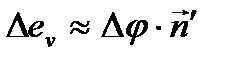 ¢, где n¢- единичный вектор, имеющий такое же направление как и Δ ev. При предельном переходе этот единичный вектор превращается в n - орт нормали к траектории в той точке, в которой была частица в момент времени t.
¢, где n¢- единичный вектор, имеющий такое же направление как и Δ ev. При предельном переходе этот единичный вектор превращается в n - орт нормали к траектории в той точке, в которой была частица в момент времени t.
|
|
Подставив в формулу (5.18.) значения 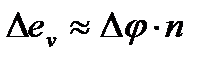 с учетом того, что
с учетом того, что 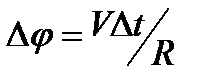 , получим:
, получим:
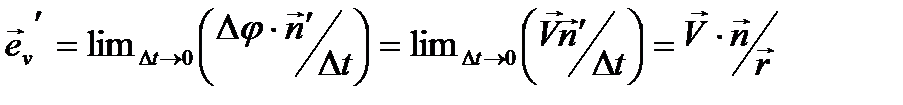
| (5.19) |
Быстрота поворота вектора скорости пропорциональна модулю скорости и кривизне траектории, (в случае окружности кривизна траектории характеризуется величиной обратной радиусу).
А формула (5.11) после подстановки в нее значения ev¢ из формулы (5.18.) примет вид:
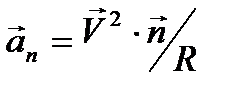
| (5.20) |
Т.е. при равномерном движении по окружности ускорение определяется формулой (5.20.) и направлено оно по нормали к мгновенной скорости. Эту составляющую ускорения называют нормальной составляющей ускорения или нормальным ускорением и обозначают индексом n.
Каждой точке произвольной криволинейной траектории можно сопоставить окружность, которая сливается с линией на бесконечно малом ее участке (рис.5.3.)
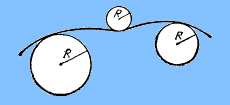
Рис. 5.3. Радиус окружности, сливающейся с траекторией на бесконечно малом ее участке, характеризует кривизну траектории
Радиус этой окружности характеризует кривизну линии в данной точке и называется радиусом кривизны.
Кривизна характеризуется величиной, обратной радиусу окружности:
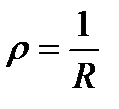
| (5.21) |
При неравномерном движении частиц по криволинейной траектории оба множителя в формуле 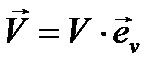 (5.9.), меняются со временем.
(5.9.), меняются со временем.
Тогда, в общем случае, ускорение распадается на два слагаемых:
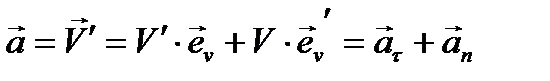
| (5.22) |
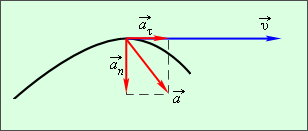
где первое слагаемое коллинеарно вектору мгновенной скорости и, следовательно, направлено по касательной к траектории - тангенциальная (касательная) составляющая ускорения - at, а второе слагаемое совпадает по направлению с нормалью к скорости - нормальная составляющая ускорения - 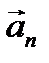 .
.
Первое слагаемое (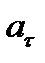 )- характеризует быстроту изменения модуля скорости, второе (
)- характеризует быстроту изменения модуля скорости, второе (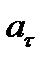 )- быстроту изменения направления скорости.
)- быстроту изменения направления скорости.
Составляющие ускорения 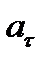 и
и 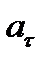 перпендикулярны друг к другу, поэтому квадрат модуля ускорения равен сумме квадратов модулей составляющих:
перпендикулярны друг к другу, поэтому квадрат модуля ускорения равен сумме квадратов модулей составляющих:
|
|
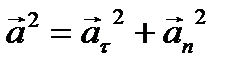 , , 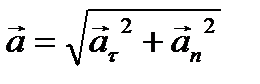
| (5.23) |
Историческая справка.
Понятие ускорения было впервые введено во французской высшей школе преподавателем Понселе, в 1841 году, который был ранее инженером французской армии.
В системе единиц СИ [a]=1 м/c2.
В зависимости от значений at и an движение можно классифицировать так;
1) ax =0, 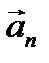 =0 - прямолинейное равномерное движение;
=0 - прямолинейное равномерное движение;
2) ax = 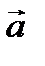 = const;
= const; 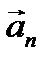 =0 - прямолинейное равнопеременное движение;
=0 - прямолинейное равнопеременное движение;
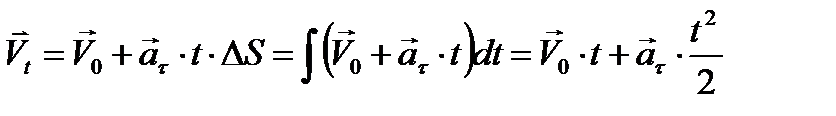
3) ax = f (x); 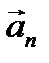 =0 - прямолинейное движение с переменным ускорением;
=0 - прямолинейное движение с переменным ускорением;
4) ax =0; 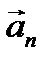 = const - равномерное движение по окружности;
= const - равномерное движение по окружности;
5) ax =0; 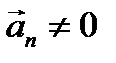 - равномерное криволинейное движение;
- равномерное криволинейное движение;
ax = const; 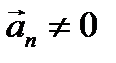 - криволинейное равнопеременное движение;
- криволинейное равнопеременное движение;
ax = f (x); 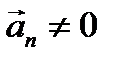 - криволинейное движение с переменным ускорением.
- криволинейное движение с переменным ускорением.
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!