Глава 1. Кинематика материальной точки
Механическое движение
Всякое изменение вообще называется движением в широком смысле слова.
Простейшей формой движения является механическое движение. Механическое движение заключается в изменении с течением времени взаимного расположения тел или частей тел друг относительно друга.
Механика - часть физики, изучающая закономерности механического движения. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564 - 1642) и окончательно сформулированы английским ученым И. Ньютоном (1643 - 1727).
Механика Галилея-Ньютона называется классической механикой, в ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме (V<<с).
Законы движения макроскопических тел со скоростями, сравнимыми со скоростью света в вакууме, изучаются релятивистской механикой, законы движения микроскопических тел (отдельные атомы и элементарные частицы) - изучаются квантовой механикой.
Механика делится на три раздела: кинематику, динамику, статику.
Кинематика изучает движение тел, не выясняя причин, его обуславливающих.
Динамика изучает законы движения тел и причины, обуславливающие это движение.
Статика изучает законы равновесия системы тел. Если известны законы движения тел, то из них можно установить и законы равновесия. Поэтому физика отдельно от законов динамики законы статики не рассматривает.
Реальные движения тел настолько сложны, что изучая их, необходимо отвлечься от несущественных для рассматриваемого движения деталей. В механике часто используют идеализации движений, а для описания движения тел в зависимости от условий конкретных задач используют разные физические модели.
Простейшими моделями являются материальная точка – МТ, макрочастица - МЧ и абсолютно твердое тело - АТТ.
Материальная точка (МТ) - тело, размерами которого можно пренебречь, считая что вся масса тела сосредоточена в одной точке.
Макроскопическая частица (МЧ) - частица образованная большим числом атомов.
Абсолютное твердое тело (АТТ) - тело, деформациями которого в условиях данной задачи можно пренебречь.
Системой отсчета (СО) называют совокупность неподвижных друг относительно друга тел, по отношению к которой рассматривается движение, и часов, связанных с ними, отсчитывающих время.
Для описания движения систему отсчета связывают с системой координат. Самая простая система - декартова система координат, три взаимно перпендикулярных оси x, y, z.
В пространственной декартовой системе координат положение частицы задается ее координатами - x, y, z.
Траекторией движения МТ называется линия, которую описывает материальная точка (частица) при своем движении.
В зависимости от формы траектории движение делят на: прямолинейное, криволинейное, по окружности.
Расстояние между точками а и b, отсчитанное вдоль траектории называется длиной пройденного пути или путем - (S ab - lab).
Перемещением - 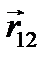 - называется направленный отрезок прямой, проведенной из начального положения в конечное.
- называется направленный отрезок прямой, проведенной из начального положения в конечное.
Перемещение характеризуется числовым значением и определенным направлением.
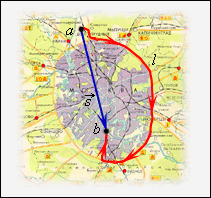
Рис. 1.1. Длина пройденного пути, при движении от точки a до точки b,
вектор перемещения 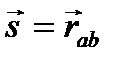
Механика ставит перед собой две основные задачи:
1. Изучение различных движений и обобщение полученных результатов в виде законов движения – законов, с помощью которых может быть предсказан характер движения в каждом конкретном случае.
2. Отыскание общих механических свойств, т.е. общих теорем или принципов, присущих любой системе, независимо от конкретного рода взаимодействий между телами системы.
Решение первой задачи привело к установлению Ньютоном и Эйнштейном так называемых динамических законов, решение же второй задачи – к обнаружению законов сохранения таких фундаментальных величин, как энергия, импульс и момент импульса.
Векторы
В физике для описания движения используют два вида физических величин: скаляры и векторы.
Физической величиной (ФВ) называется
Скаляры - величины, определяемые лишь числовым значением.
Примеры СФВ: масса - m, время - t, энергия - W и т.д.
Величины, характеризующиеся числовым значением, определенным, направлением и складывающиеся по правилу параллелограмма, называется векторами. Они играют в физике большую роль.
Векторы обозначаются буквами со стрелкой над ней: 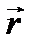 ,
, 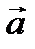 ,
, 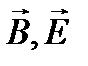 или, при письме, буквой с черточкой над ней:
или, при письме, буквой с черточкой над ней: 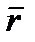 .
.
ПримерыВФВ: вектор перемещения - 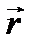 , вектор линейного ускорения -
, вектор линейного ускорения - 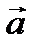 , вектор скорости -
, вектор скорости - 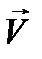 , вектор напряженности электрического поля -
, вектор напряженности электрического поля - 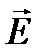 , вектор магнитной индукции -
, вектор магнитной индукции - 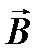 и т.д.
и т.д.
Модулем вектора - называется числовое значение вектора.
Модуль вектора - всегда положительный скаляр.
Модуль вектора обозначается той же буквой обычного шрифта либо буквой полужирного шрифта, по бокам которой ставят вертикальные черточки:
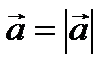 - модуль вектора
- модуль вектора 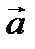 .
.
Во всех случаях, когда это возможно, модуль вектора нужно обозначать буквой обычного шрифта. Однако, в некоторых случаях модуль можно обозначать только с помощью боковых черточек.
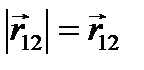 - обозначение модуля вектора перемещения.
- обозначение модуля вектора перемещения.
Свободный вектор - вектор, который может быть отложен из любой точки пространства.
Рассмотрим три свободных вектора 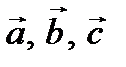 .
.
Векторы, направленные вдоль параллельных прямых (в одну и ту же, либо в противоположные стороны) называются коллинеарными.

Рис. 2.1. Коллинеарные векторы 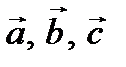 направлены вдоль параллельных прямых
направлены вдоль параллельных прямых
Путем переноса коллинеарные векторы могут быть расположены на одной и той же прямой.
Векторы, лежащие в параллельных плоскостях называются компланарными.

Рис. 2.2. Между векторами 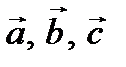 имеются соотношения:
имеются соотношения: 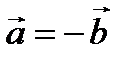 ,
, 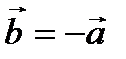 ,
, 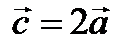 ,
, 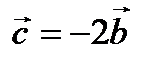
Векторы нельзя сравнивать друг с другом, не бывает положительных и отрицательных векторов, невозможны равенства вида 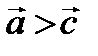 .
.
Сравнивать можно модули векторов.
Соотношение 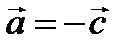 означает лишь, что векторы
означает лишь, что векторы 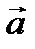 и
и 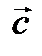 имеют одинаковые модули, а направления этих векторов противоположны.
имеют одинаковые модули, а направления этих векторов противоположны.
Действия над векторами
Пусть у нас имеются два свободных вектора 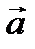 и
и 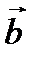 . Произведем над этими векторами операции сложения, вычитания, умножения.
. Произведем над этими векторами операции сложения, вычитания, умножения.
1. Сложение векторов. Складывать два вектора можно двумя способами - по правилам треугольника и параллелограмма.
· Правило треугольника. Если начало второго вектора совместить с концом первого, то вектор, проведенный из начала первого в конец второго будет являться суммой двух векторов. 
Рис.2.3. Правило треугольника. Вектор 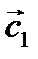 является суммой векторов
является суммой векторов 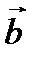 и
и 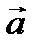
· Правило параллелограмма. Если оба вектора выходят из одной точки, то суммой векторов будет вектор 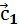 , выходящий из общей точки и совпадающий с диагональю параллелограмма, сторонами которого являются два исходных вектора.
, выходящий из общей точки и совпадающий с диагональю параллелограмма, сторонами которого являются два исходных вектора.

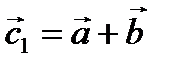 (2.1)
(2.1)
Рис. 2.4. Правило параллелограмма. Вектор 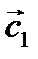 является суммой векторов
является суммой векторов 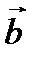 и
и 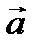
2. Вычитание векторов: 
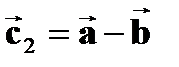 (2.2).
(2.2).
Разностью векторов 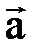 и
и 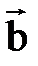 называется вектор
называется вектор 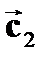 , который в сумме с вектором
, который в сумме с вектором 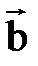 даёт вектор
даёт вектор 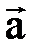 .
.





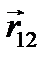 - называется направленный отрезок прямой, проведенной из начального положения в конечное.
- называется направленный отрезок прямой, проведенной из начального положения в конечное.
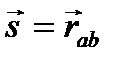
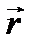 ,
, 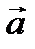 ,
, 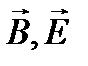 или, при письме, буквой с черточкой над ней:
или, при письме, буквой с черточкой над ней: 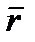 .
.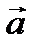 , вектор скорости -
, вектор скорости - 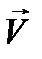 , вектор напряженности электрического поля -
, вектор напряженности электрического поля - 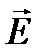 , вектор магнитной индукции -
, вектор магнитной индукции - 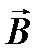 и т.д.
и т.д.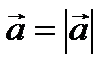 - модуль вектора
- модуль вектора 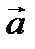 .
.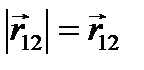 - обозначение модуля вектора перемещения.
- обозначение модуля вектора перемещения.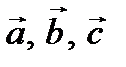 .
. 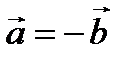 ,
, 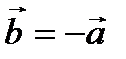 ,
, 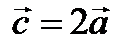 ,
, 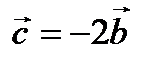
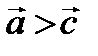 .
.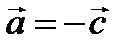 означает лишь, что векторы
означает лишь, что векторы 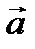 и
и 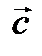 имеют одинаковые модули, а направления этих векторов противоположны.
имеют одинаковые модули, а направления этих векторов противоположны.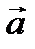 и
и 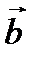 . Произведем над этими векторами операции сложения, вычитания, умножения.
. Произведем над этими векторами операции сложения, вычитания, умножения.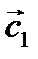 является суммой векторов
является суммой векторов 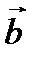 и
и 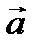
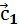 , выходящий из общей точки и совпадающий с диагональю параллелограмма, сторонами которого являются два исходных вектора.
, выходящий из общей точки и совпадающий с диагональю параллелограмма, сторонами которого являются два исходных вектора.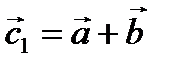 (2.1)
(2.1)
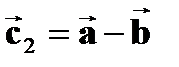 (2.2).
(2.2).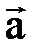 и
и 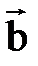 называется вектор
называется вектор 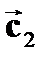 , который в сумме с вектором
, который в сумме с вектором 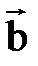 даёт вектор
даёт вектор  .
.


