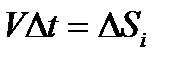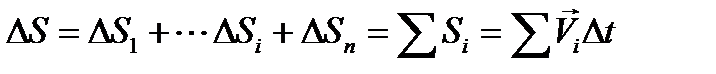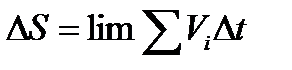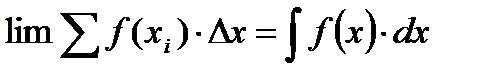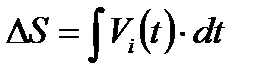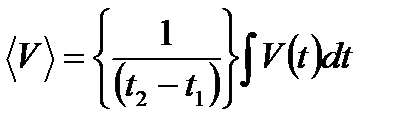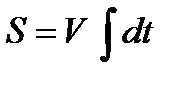Этот способ применяют тогда, когда траектория точки известна заранее. Положение точки А определяют дуговой координатой 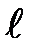 – расстоянием вдоль траектории от выбранного начала отсчета до данной точки (Рис.3.2). При этом устанавливают (произвольно) положительное направление отсчета координаты l, например так, как показано стрелкой на траектории.
– расстоянием вдоль траектории от выбранного начала отсчета до данной точки (Рис.3.2). При этом устанавливают (произвольно) положительное направление отсчета координаты l, например так, как показано стрелкой на траектории.
Выберем единичный вектор 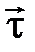 в точке А, направленной по касательной к траектории в данной точке в сторону возрастания дуговой координаты.
в точке А, направленной по касательной к траектории в данной точке в сторону возрастания дуговой координаты.
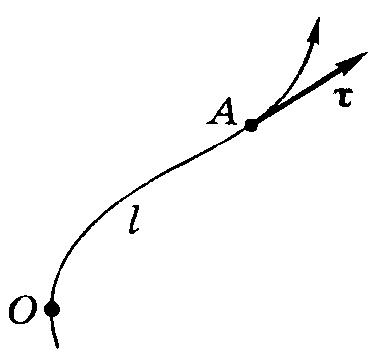
Рис. 3.2.
Движение точки определено, если:
· известна ее траектория;
· начало отсчета О;
· положительное направление дуговой координаты l;
· и закон движения точки, т.е. зависимость l = l (t).
Скорость
Для характеристики движения МТ вводится векторная величина - скорость. Она характеризует как быстроту движения, так и его направление в данный момент. Рассмотрим движение МТ по некоторой криволинейной траектории.
В момент времени t положение МТ характеризуется –
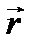 1
1; в
(t +Δ t) 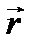 2
2; за промежуток времени
Δ t МТ проходит путь
Δ S, а радиус вектор получает приращение -
Δ 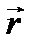
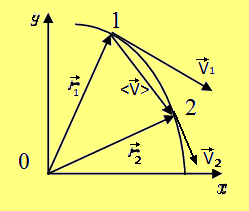
Рис. 4.1. Направление векторов скоростей: средней - < 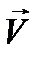 > и мгновенных -
> и мгновенных - 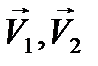
Равномерным движением - называется такое движение, при котором за любые равные, сколь угодно малые промежутки времени Dt частица (МТ) проходит одинаковые пути - DS.
Вектор скорости равномерного движения определяется формулой (4.1):
|
| 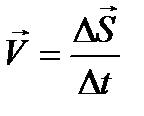
| (4.1)
|
Модуль вектора скорости равномерного движения - равен пути, проходимому в единицу времени.
Для неравномерного движения вводят понятие модуля средней скорости (среднюю путевую скорость) и вектора средней скорости.
Вектор средней скорости определяется соотношением:
|
| 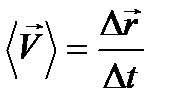 ; ; 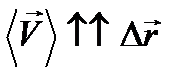
| (4.2)
|
Средняя путевая скорость равна:
|
| 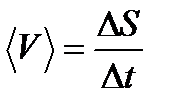
| (4.3)
|
Для прямолинейного движения: 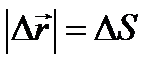 и тогда
и тогда
|
| 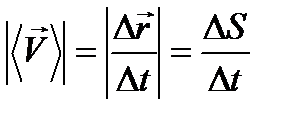
| (4.4)
|
Чтобы определить скорость в некоторый момент времени t, необходимо чтобы промежуток времени движения Dt→0, тогда средняя скорость устремится к предельному значению, называемому мгновенной скоростью.
Вектор мгновенной скорости, это ВФВ, равная первой производной радиуса - вектора движущейся МТ по времени:
|
| 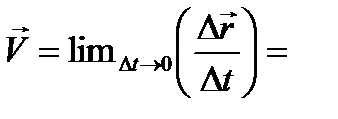 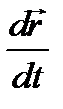
| (4.5)
|
Вектор мгновенной скорости совпадает по направлению с касательной, проведенной к траектории в данную точку, и направлен в сторону движения.
Модуль вектора мгновенной скорости равен модулю первой производной радиус-вектора по времени (формула (4.6.)).
|
| 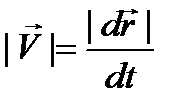
| (4.6)
|
Но радиус-вектор в общем случае можно представить в виде векторной суммы трех составляющих (4.7)
|
| 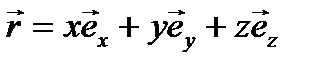
| (4.7)
|
Тогда вектор мгновенной скорости будет равен (4.8):
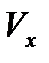 ,
, 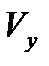 ,
, 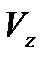 - проекции вектора мгновенной скорости на соответствующие координатные оси или ее компоненты.
- проекции вектора мгновенной скорости на соответствующие координатные оси или ее компоненты.
Из формулы (4.9.)следует: компоненты скорости равны производным соответствующих координат по времени.
Зная модуль скорости в каждый момент времени, можно вычислить путь, пройденный МТ (частицей) за промежуток времени Δt=t2-t1. Разобьем этот промежуток времени на N малых промежутков, обозначим 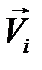 , ti- модуль скорости и время i -го участка, i пробегает значения от 1 до N. Тогда:
, ti- модуль скорости и время i -го участка, i пробегает значения от 1 до N. Тогда:
|
| 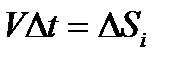
| (4.10)
|
а весь пройденный путь:
|
| 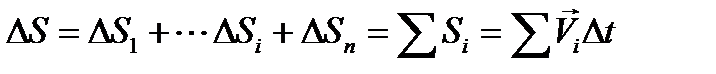
| (4.11)
|
Если Dt®0, то:
|
| 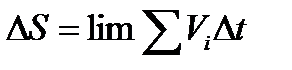
| (4.12)
|
В математике выражение вида (4.13):
|
| 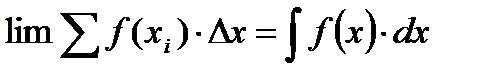
| (4.13)
|
составленное для значений x, заключенных в пределах от x1=a до x2=b называют определенным интегралом от функции f(x) взятым по переменной x между нижним x1=a и верхним x2=b пределами.
Тогда длину пройденного пути можно представить так:
|
| 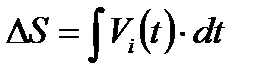
| (4.14)
|
Определенный интеграл (4.14.) численно равен площади фигуры, ограниченной кривой V(t), осью t, и с боков прямыми: t = t 1, t = t 2.
Векторную функцию в виде графика изобразить нельзя.
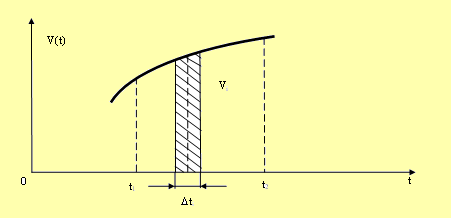
Рис.4.3. Площадь заштрихованной полоски приближенно равна ViΔti
Средняя скорость определяется формулой:
|
| 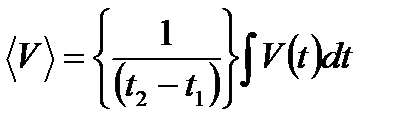
| (4.15)
|
Аналогично вычисляются средние значения любых скалярных или векторных функций.
Если движение равномерное, то длина пройденного пути равна:
|
| 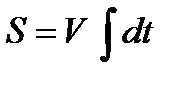
| (4.16)
|





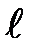 – расстоянием вдоль траектории от выбранного начала отсчета до данной точки (Рис.3.2). При этом устанавливают (произвольно) положительное направление отсчета координаты l, например так, как показано стрелкой на траектории.
– расстоянием вдоль траектории от выбранного начала отсчета до данной точки (Рис.3.2). При этом устанавливают (произвольно) положительное направление отсчета координаты l, например так, как показано стрелкой на траектории.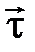 в точке А, направленной по касательной к траектории в данной точке в сторону возрастания дуговой координаты.
в точке А, направленной по касательной к траектории в данной точке в сторону возрастания дуговой координаты.
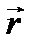 1; в (t +Δ t)
1; в (t +Δ t) 
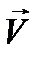 > и мгновенных -
> и мгновенных - 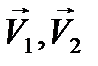
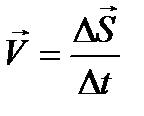
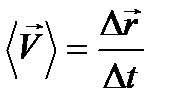 ;
; 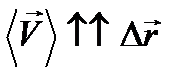
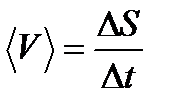
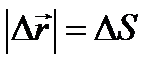 и тогда
и тогда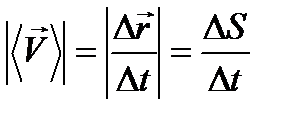
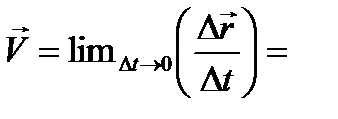
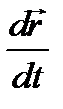
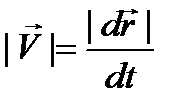
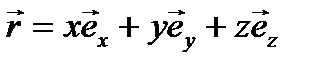
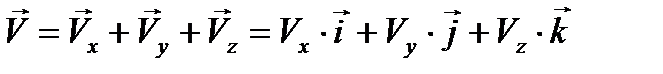
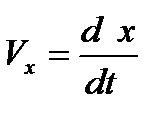 ,
, 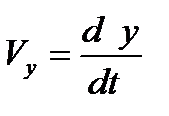 ,
, 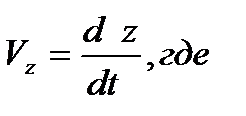
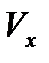 ,
, 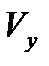 ,
, 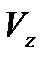 - проекции вектора мгновенной скорости на соответствующие координатные оси или ее компоненты.
- проекции вектора мгновенной скорости на соответствующие координатные оси или ее компоненты.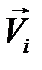 , ti- модуль скорости и время i -го участка, i пробегает значения от 1 до N. Тогда:
, ti- модуль скорости и время i -го участка, i пробегает значения от 1 до N. Тогда: