Минором некоторого элемента определителя n -го порядка называется определитель (n -1) -го порядка, получающийся их исходного определителя путем вычеркивания столбца и строки, на пересечении которых находится рассматриваемый элемент.
Алгебраическим дополнением некоторого элемента определителя  называется его минор, взятый со своим или противоположным знаком по следующему правилу
называется его минор, взятый со своим или противоположным знаком по следующему правилу 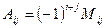 , где
, где 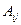 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента  ,
, 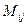 - минор этого элемента.
- минор этого элемента.
П р и м е р. Для определителя четвертого порядка
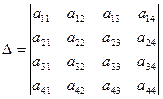
найти миноры и алгебраические дополнения элементов 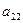 и
и 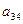 .
.
Р е ш е н и е.
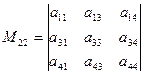 ,
,  ,
,
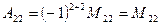 ,
, 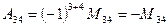 .
.
Правило разложения определителя по элементам некоторого ряда: всякий определитель равен сумме произведений элементов некоторого (любого) ряда на их алгебраические дополнения.
Так, например,
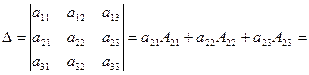
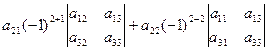 +
+ 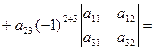
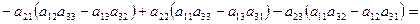
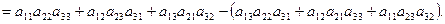
Записано разложение определителя третьего порядка по элементам второй строки. Последняя строка, в приведенных вычислениях, полностью совпадает со значением определителя, вычисленного ранее по правилу Саррюса.
Таким образом, определяя определитель n – го порядка, как квадратную структуру состоящую из 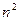 элементов, расположенных в n столбцах и n строках, сможем вычислять такие определители путем последовательного понижения порядков, разлагая их по элементам того или иного ряда.
элементов, расположенных в n столбцах и n строках, сможем вычислять такие определители путем последовательного понижения порядков, разлагая их по элементам того или иного ряда.
П р и м е р.
Для данного определителя 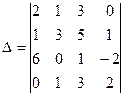
найти миноры и алгебраические дополнения элементов 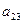 и
и 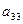 .
.
Используя свойства определителей, вычислить определитель 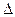 :
:
a) разложив его по элементам второй строки;
б) разложив его по элементам третьего столбца;
в) получив предварительно нули во второй строке;
г) получив предварительно нули под главной диагональю.
Р е ш е н и е.
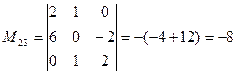 ,
, 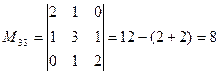 ,
,
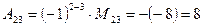 ,
, 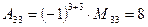 .
.
а) 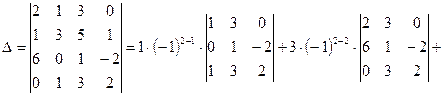
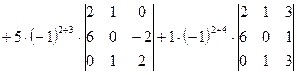 =
=
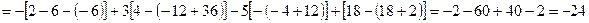 .
.
б) 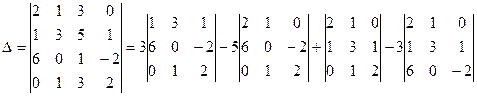 =
=
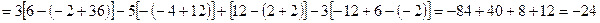 .
.
в) 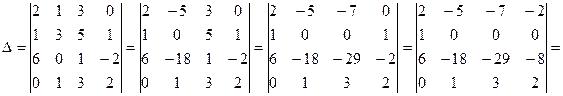
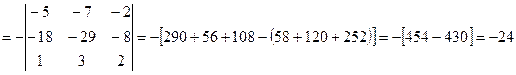 .
.
Последовательно из первого определителя получили второй определитель путем прибавления к элементам второго столбца соответствующих элементов первого столбца умноженных на -3 (получили во втором определителе 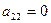 ). Из второго определителя получили третий путем прибавления к элементам третьего столбца соответствующих элементов первого столбца умноженных на -5 (получили в третьем определителе
). Из второго определителя получили третий путем прибавления к элементам третьего столбца соответствующих элементов первого столбца умноженных на -5 (получили в третьем определителе 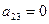 ). Из третьего определителя получили четвертый путем прибавления к элементам четвертого столбца соответствующих элементов первого столбца домноженных на -1 (получили в четвертом определителе
). Из третьего определителя получили четвертый путем прибавления к элементам четвертого столбца соответствующих элементов первого столбца домноженных на -1 (получили в четвертом определителе  ). Теперь вторая строка определителя содержит три нулевых элемента, и определитель четвертого порядка представляется одним определителем третьего порядка (при разложении по элементам второй строки).
). Теперь вторая строка определителя содержит три нулевых элемента, и определитель четвертого порядка представляется одним определителем третьего порядка (при разложении по элементам второй строки).
г) 
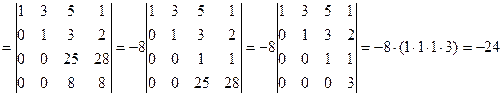 .
.
Последовательно из первого определителя получили второй определитель путем перестановки местами первой и второй строки (во втором определителе получили 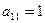 ). Из второго определителя получили третий путем прибавления к элементам второй и третьей строки соответствующих элементов первой строки, предварительно домножив их соответственно на -2 и -6 (получили в третьем определителе
). Из второго определителя получили третий путем прибавления к элементам второй и третьей строки соответствующих элементов первой строки, предварительно домножив их соответственно на -2 и -6 (получили в третьем определителе 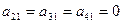 ). Из третьего определителя получили четвертый путем перестановки местами второй и четвертой строк (получили в четвертом определителе
). Из третьего определителя получили четвертый путем перестановки местами второй и четвертой строк (получили в четвертом определителе 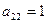 ). Из четвертого пятый определитель получили путем прибавления к элементам третьей и четвертой строк соответствующих элементов второй строки, предварительно помножив их соответственно на 18 и на 5 (получили в пятом определителе
). Из четвертого пятый определитель получили путем прибавления к элементам третьей и четвертой строк соответствующих элементов второй строки, предварительно помножив их соответственно на 18 и на 5 (получили в пятом определителе 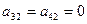 ). Из пятого определителя получили шестой путем вынесения за знак определителя восьмерки - общего для четвертой строки множителя и перестановки местами третьей и четвертой строк (получили в шестом определителе
). Из пятого определителя получили шестой путем вынесения за знак определителя восьмерки - общего для четвертой строки множителя и перестановки местами третьей и четвертой строк (получили в шестом определителе 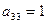 ). Из шестого определителя седьмой получили путем прибавления к элементам четвертой строки соответствующих элементов третьей строки, предварительно домножив их на -25 (получили в седьмом определителе
). Из шестого определителя седьмой получили путем прибавления к элементам четвертой строки соответствующих элементов третьей строки, предварительно домножив их на -25 (получили в седьмом определителе 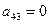 ). У последнего седьмого определителя под главной диагональю имеем нули, а такой определитель равен произведению элементов стоящих на главной диагонали.
). У последнего седьмого определителя под главной диагональю имеем нули, а такой определитель равен произведению элементов стоящих на главной диагонали.
Матрицы
Основные определения
Матрицей размерности m 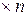 называется прямоугольная таблица элементов, расположенных в m строках и n столбцах:
называется прямоугольная таблица элементов, расположенных в m строках и n столбцах:
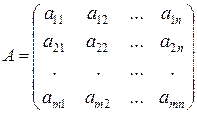 .
.
Элементами матрицы могут быть необязательно числа. Однако в математике нас интересуют, как правило, числовые матрицы.
Если m = 1, то имеем матрицу-строку
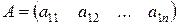 .
.
Если n = 1, то имеем матрицу-столбец
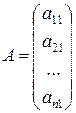 .
.
Если n =т= n, то имеем квадратную матрицу n -го порядка
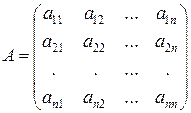 .
.
В квадратной матрице различают элементы 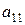 ,
, 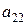 ,...,
,..., 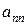 , стоящие на главной диагонали матрицы и элементы
, стоящие на главной диагонали матрицы и элементы 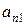 ,
, 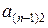 ,...,
,..., 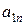 , стоящие на побочной диагонали.
, стоящие на побочной диагонали.
Если в квадратной матрице все элементы, кроме элементов стоящих на главной диагонали, равны нулю, то матрица называется диагональной
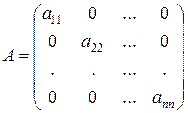 .
.
Если элементы диагональной матрицы, стоящие на главной диагонали, равны единицам, то матрица называется единичной матрицей соответствующего порядка и обозначается через Е:
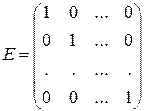 .
.
Две матрицы равны тогда и только тогда, когда они имеют одинаковую размерность и когда в одинаковых ячейках (на одинаковых местах) матриц стоят одинаковые элементы.
Действия с матрицами
Умножение матрицы на число. При умножении матрицы на число, все элементы матрицы множатся на это число
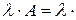
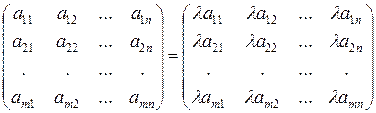 .
.
Таким образом, сомножитель общий для всех элементов матрицы можно выносить за знак матрицы.
Сложение матриц. Складываться могут лишь матрицы одинаковой размерности. При сложении двух матриц одинаковой размерности, складываются их соответствующие элементы
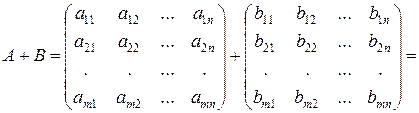
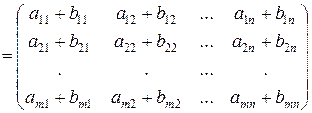 .
.
При вычитании двух матриц одинаковой размерности, из элементов матрицы-уменьшаемого вычитаются соответствующие элементы матрицы-вычитаемого.
Перемножение матриц. Пусть имеем две матрицы A - первая матрица-сомножитель (матрица-множимое) и B - вторая матрица-сомножитель (матрица-множитель). Операция умножения матриц 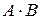 имеет смысл только тогда, когда количество столбцов матрицы-множимого (матрицы А) равно количеству строк матрицы-множителя (матрицы B). В результате умножения двух матриц получаем новую матрицу С, элемент которой
имеет смысл только тогда, когда количество столбцов матрицы-множимого (матрицы А) равно количеству строк матрицы-множителя (матрицы B). В результате умножения двух матриц получаем новую матрицу С, элемент которой 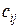 (элемент, стоящий в i – той строке и в j– том столбце матрицы-произведения) получается как результат суммирования произведений элементов i –той строки матрицы А на соответствующие элементы j– того столбца матрицы В, например,
(элемент, стоящий в i – той строке и в j– том столбце матрицы-произведения) получается как результат суммирования произведений элементов i –той строки матрицы А на соответствующие элементы j– того столбца матрицы В, например,
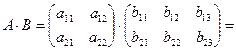
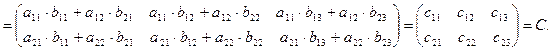
Таким образом, например, 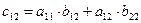 . Матрица А имеет два столбца, матрица В имеет две строки и поэтому их перемножение возможно. Матрица-произведение С содержит столько строк, сколько их имеет матрица-множимое А и столько столбцов сколько их имеет матрица множитель В.
. Матрица А имеет два столбца, матрица В имеет две строки и поэтому их перемножение возможно. Матрица-произведение С содержит столько строк, сколько их имеет матрица-множимое А и столько столбцов сколько их имеет матрица множитель В.
П р и м е р 1.
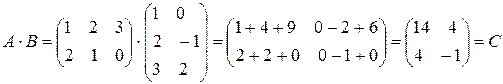 .
.
П р и м е р 2.
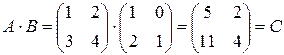 .
.
П р и м е р 3.
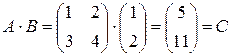 .
.
Обращение матриц. Квадратной матрице 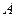 , можно поставить в соответствие ее определитель. Так, например, если матрица имеет вид
, можно поставить в соответствие ее определитель. Так, например, если матрица имеет вид
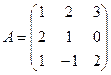 ,
,
то соответствующий ей определитель (детерминант) будет
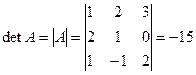 .
.
В случае, если 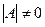 , говорят, что матрица А невырожденная или неособенная, если
, говорят, что матрица А невырожденная или неособенная, если 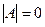 , то А – вырожденная или особенная матрица.
, то А – вырожденная или особенная матрица.
Квадратная матрица 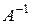 называется обратной по отношению к квадратной матрице А, если их произведение дает единичную матрицу соответствующего порядка
называется обратной по отношению к квадратной матрице А, если их произведение дает единичную матрицу соответствующего порядка 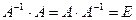 .
.
Необходимое и достаточное условие существования обратной матрицы. Для того чтобы квадратная матрица А имела обратную матрицу необходимо и достаточно, чтобы матрица А была невырожденной.
Схема отыскания обратной матрицы
1. Для квадратной матрицы А находится 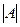 . Убеждаемся, что последний определитель не равен нулю.
. Убеждаемся, что последний определитель не равен нулю.
2. Строится матрица В – матрица алгебраических дополнений членов определителя 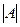 .
.
3. Строится матрица 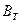 - транспонированная матрица В.
- транспонированная матрица В.
4. Строится матрица 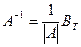 .
.
П р и м е р. Найти обратную матрицу для матрицы
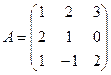 .
.
Р е ш е н и е.
1. 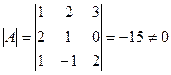 .
.
2. Находим алгебраические дополнения элементов определителя 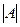 :
:
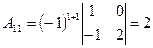 ,
, 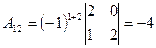 ,
, 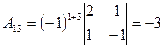 ,
,
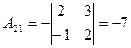 ,
, 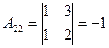 ,
, 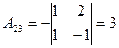 ,
,
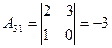 ,
, 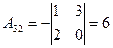 ,
, 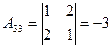 .
.
Теперь
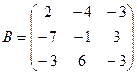 .
.
3. 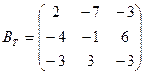 .
.
4. 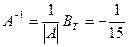
 .
.
П р о в е рк а:
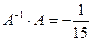
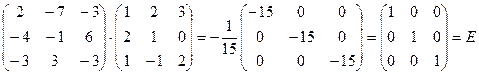 .
.
В результате перемножения А на 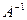 получили единичную матрицу, следовательно обратная матрица найдена верно.
получили единичную матрицу, следовательно обратная матрица найдена верно.



 называется его минор, взятый со своим или противоположным знаком по следующему правилу
называется его минор, взятый со своим или противоположным знаком по следующему правилу 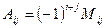 , где
, где 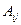 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 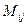 - минор этого элемента.
- минор этого элемента.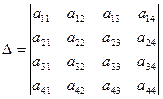
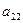 и
и 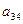 .
.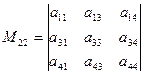 ,
,  ,
,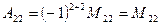 ,
, 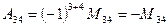 .
.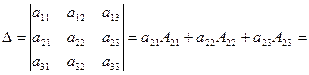
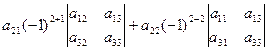 +
+ 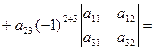
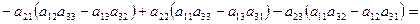
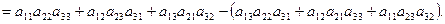
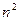 элементов, расположенных в n столбцах и n строках, сможем вычислять такие определители путем последовательного понижения порядков, разлагая их по элементам того или иного ряда.
элементов, расположенных в n столбцах и n строках, сможем вычислять такие определители путем последовательного понижения порядков, разлагая их по элементам того или иного ряда.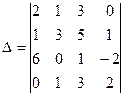
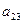 и
и 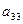 .
.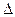 :
: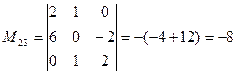 ,
, 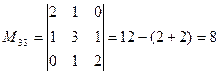 ,
,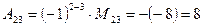 ,
, 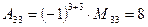 .
.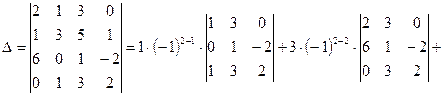
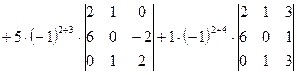 =
=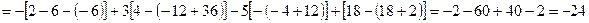 .
.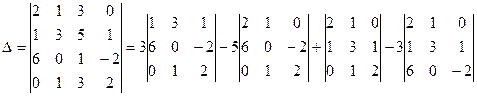 =
=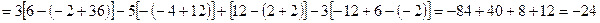 .
.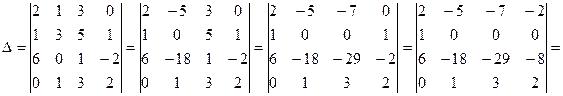
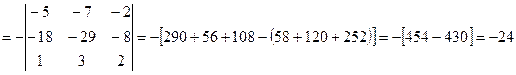 .
.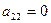 ). Из второго определителя получили третий путем прибавления к элементам третьего столбца соответствующих элементов первого столбца умноженных на -5 (получили в третьем определителе
). Из второго определителя получили третий путем прибавления к элементам третьего столбца соответствующих элементов первого столбца умноженных на -5 (получили в третьем определителе 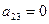 ). Из третьего определителя получили четвертый путем прибавления к элементам четвертого столбца соответствующих элементов первого столбца домноженных на -1 (получили в четвертом определителе
). Из третьего определителя получили четвертый путем прибавления к элементам четвертого столбца соответствующих элементов первого столбца домноженных на -1 (получили в четвертом определителе 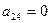 ). Теперь вторая строка определителя содержит три нулевых элемента, и определитель четвертого порядка представляется одним определителем третьего порядка (при разложении по элементам второй строки).
). Теперь вторая строка определителя содержит три нулевых элемента, и определитель четвертого порядка представляется одним определителем третьего порядка (при разложении по элементам второй строки).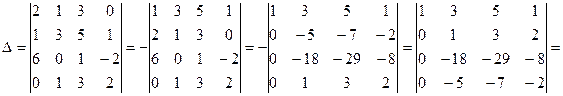
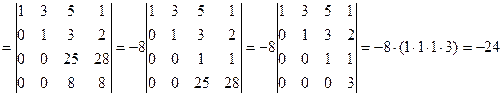 .
.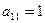 ). Из второго определителя получили третий путем прибавления к элементам второй и третьей строки соответствующих элементов первой строки, предварительно домножив их соответственно на -2 и -6 (получили в третьем определителе
). Из второго определителя получили третий путем прибавления к элементам второй и третьей строки соответствующих элементов первой строки, предварительно домножив их соответственно на -2 и -6 (получили в третьем определителе 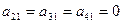 ). Из третьего определителя получили четвертый путем перестановки местами второй и четвертой строк (получили в четвертом определителе
). Из третьего определителя получили четвертый путем перестановки местами второй и четвертой строк (получили в четвертом определителе 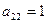 ). Из четвертого пятый определитель получили путем прибавления к элементам третьей и четвертой строк соответствующих элементов второй строки, предварительно помножив их соответственно на 18 и на 5 (получили в пятом определителе
). Из четвертого пятый определитель получили путем прибавления к элементам третьей и четвертой строк соответствующих элементов второй строки, предварительно помножив их соответственно на 18 и на 5 (получили в пятом определителе 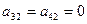 ). Из пятого определителя получили шестой путем вынесения за знак определителя восьмерки - общего для четвертой строки множителя и перестановки местами третьей и четвертой строк (получили в шестом определителе
). Из пятого определителя получили шестой путем вынесения за знак определителя восьмерки - общего для четвертой строки множителя и перестановки местами третьей и четвертой строк (получили в шестом определителе 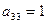 ). Из шестого определителя седьмой получили путем прибавления к элементам четвертой строки соответствующих элементов третьей строки, предварительно домножив их на -25 (получили в седьмом определителе
). Из шестого определителя седьмой получили путем прибавления к элементам четвертой строки соответствующих элементов третьей строки, предварительно домножив их на -25 (получили в седьмом определителе 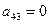 ). У последнего седьмого определителя под главной диагональю имеем нули, а такой определитель равен произведению элементов стоящих на главной диагонали.
). У последнего седьмого определителя под главной диагональю имеем нули, а такой определитель равен произведению элементов стоящих на главной диагонали.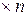 называется прямоугольная таблица элементов, расположенных в m строках и n столбцах:
называется прямоугольная таблица элементов, расположенных в m строках и n столбцах: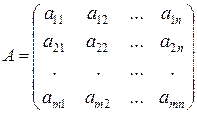 .
. 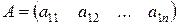 .
.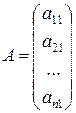 .
.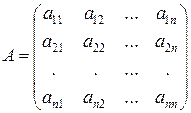 .
.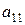 ,
, 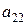 ,...,
,..., 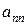 , стоящие на главной диагонали матрицы и элементы
, стоящие на главной диагонали матрицы и элементы 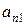 ,
, 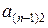 ,...,
,..., 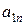 , стоящие на побочной диагонали.
, стоящие на побочной диагонали.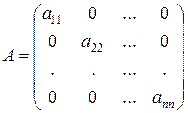 .
.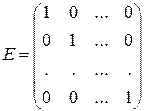 .
.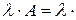
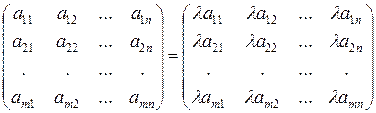 .
.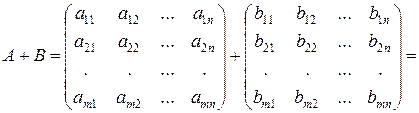
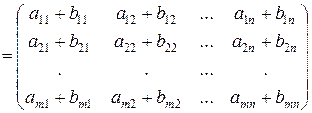 .
.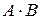 имеет смысл только тогда, когда количество столбцов матрицы-множимого (матрицы А) равно количеству строк матрицы-множителя (матрицы B). В результате умножения двух матриц получаем новую матрицу С, элемент которой
имеет смысл только тогда, когда количество столбцов матрицы-множимого (матрицы А) равно количеству строк матрицы-множителя (матрицы B). В результате умножения двух матриц получаем новую матрицу С, элемент которой 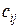 (элемент, стоящий в i – той строке и в j– том столбце матрицы-произведения) получается как результат суммирования произведений элементов i –той строки матрицы А на соответствующие элементы j– того столбца матрицы В, например,
(элемент, стоящий в i – той строке и в j– том столбце матрицы-произведения) получается как результат суммирования произведений элементов i –той строки матрицы А на соответствующие элементы j– того столбца матрицы В, например,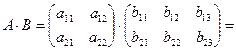
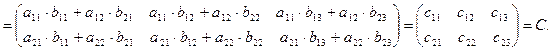
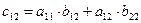 . Матрица А имеет два столбца, матрица В имеет две строки и поэтому их перемножение возможно. Матрица-произведение С содержит столько строк, сколько их имеет матрица-множимое А и столько столбцов сколько их имеет матрица множитель В.
. Матрица А имеет два столбца, матрица В имеет две строки и поэтому их перемножение возможно. Матрица-произведение С содержит столько строк, сколько их имеет матрица-множимое А и столько столбцов сколько их имеет матрица множитель В.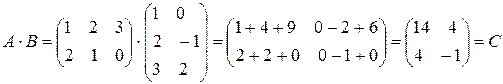 .
.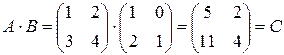 .
.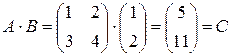 .
.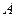 , можно поставить в соответствие ее определитель. Так, например, если матрица имеет вид
, можно поставить в соответствие ее определитель. Так, например, если матрица имеет вид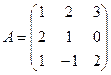 ,
,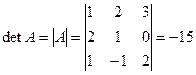 .
.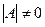 , говорят, что матрица А невырожденная или неособенная, если
, говорят, что матрица А невырожденная или неособенная, если 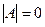 , то А – вырожденная или особенная матрица.
, то А – вырожденная или особенная матрица.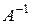 называется обратной по отношению к квадратной матрице А, если их произведение дает единичную матрицу соответствующего порядка
называется обратной по отношению к квадратной матрице А, если их произведение дает единичную матрицу соответствующего порядка 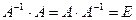 .
.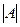 . Убеждаемся, что последний определитель не равен нулю.
. Убеждаемся, что последний определитель не равен нулю.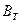 - транспонированная матрица В.
- транспонированная матрица В.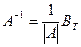 .
.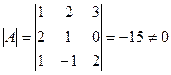 .
.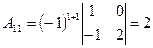 ,
, 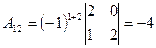 ,
, 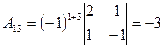 ,
,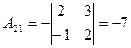 ,
, 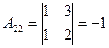 ,
, 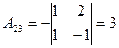 ,
,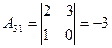 ,
, 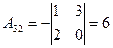 ,
, 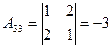 .
.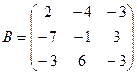 .
.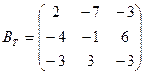 .
.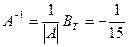
 .
.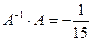
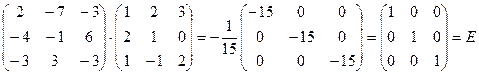 .
.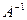 получили единичную матрицу, следовательно обратная матрица найдена верно.
получили единичную матрицу, следовательно обратная матрица найдена верно.


