В.Н.Филатов
ВЫСШАЯ МАТЕМАТИКА
Учебное пособие 1
К изучению курса
для студентов специальности 290800
Саратов – 2005
УДК 512+514+517(075)
ББК 22.11
Ф 51
Рецензенты:
Институт повышения квалификации и переподготовки работников образования (доктор физико-математических наук, профессор В.А.Молчанов)
Доктор физико-математических наук, профессор
Саратовского государственного университета А.И.Землянухин
Одобрено
редакционно-издательским советом
Саратовского государственного технического университета
Филатов В.Н.
Ф 51 Высшая математика: учеб. пособие.
/ В.Н.Филатов. Саратов: Сарат. гос. тех. ун-т, 2005. – 72 с.
ISBN 5-7433-1455-1
В учебном пособии приводятся формулировки теорем, определения, формулы и понятия по линейной и векторной алгебре, аналитической геометрии и введению в анализ - материал, осваиваемый студентами в первом семестре обучения.
Предназначено для методического обеспечения курса вышей математики и может быть полезным при подготовке к практическим занятиям, зачетам, коллоквиумам и экзаменам.
УДК 512+514+517(075)
ББК 22.11
C Саратовский государственный
технический университет, 2005
ISBN 5-7433-1455-1 C Филатов В.Н., 2005
ПРЕДИСЛОВИЕ
Учебное пособие издается в соответствии с постановлением учебно-методической комиссии по специальности «Водоснабжение и водоотведение» (протокол № от июня 2003 г.) и редакционно-издательского совета СГТУ. По мнению УМКС ВиВ в настоящее время по многим дисциплинам интенсивность обучения заметно снизилась. Тому есть много причин:
- недостатки школьного образования;
- возможность поступить на определенные виды образования без конкурсного отбора;
- резкая недостаточность централизованного издания учебников и учебных пособий.
Особенно это присуще обучению студентов на трех начальных курсах. Отмечено, что заметную роль в успешном изучении дисциплины играет быстрота и степень усвоения основных ее понятий. Студенты первых курсов еще не владеют навыками точного переноса понятия или определения в свой конспект, быстрого отыскания их в учебной литературе. Они при подготовке к экзаменам или отчету по модулям затрачивают на это неоправданно много времени.
Цель данного собрания понятий и определений по дисциплине «Высшая математика» заключается в облегчении их поиска, усвоению формулировок и овладением способностью свободной их трактовке и применению. В сборнике помещены рисунки, облегчающие понимание формул и определений. К минимуму в пособии сведено решение примеров, которые также решаются для пояснения определений и свойств математических понятий.
Все замечания и предложения, направленные на улучшение и пополнение учебного пособия будут приняты с благодарностью, обсуждены на заседании УМКС ВиВ и учтены в последующей работе над совершенствованием пособия.
Председатель УМКС ВиВ,
профессор Л.И. Высоцкий
Свойства определителей
Сформулируем свойства и проследим их выполнение на числовых примерах.
1. Определитель не изменит своего значения, если в нем строки заменить соответствующими столбцами. Определитель, в котором строки заменены соответствующими столбцами, называется транспонированным по отношению к исходному определителю.
П р и м е р. Пусть исходный определитель
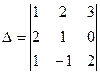 .
.
Тогда транспонированный определитель
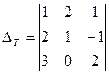 .
.
Первая строка определителя 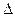 стала первым столбцом определителя
стала первым столбцом определителя 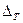 . Первый, второй, третий (слева направо) элементы этой первой строки в
. Первый, второй, третий (слева направо) элементы этой первой строки в 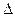 стали соответственно первым, вторым, третьим (сверху вниз) элементами первого столбца в
стали соответственно первым, вторым, третьим (сверху вниз) элементами первого столбца в 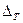 . Аналогично строятся второй и третий столбцы определителя
. Аналогично строятся второй и третий столбцы определителя 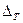 . Определитель
. Определитель 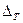 получится из определителя
получится из определителя 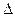 , если элементы определителя
, если элементы определителя 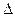 повернуть относительно главной диагонали, как вокруг фиксированной оси, на
повернуть относительно главной диагонали, как вокруг фиксированной оси, на 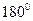 .
.
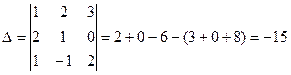 ,
, 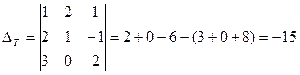 .
.
Таким образом, на примере показали, что 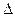 =
= 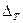 .
.
Из этого первого свойства следует равноправие строк и столбцов в определителе и впредь мы будем их называть рядами.
2. Если в определителе поменять местами два параллельных ряда, то знак определителя изменится на противоположный, абсолютная величина его не изменится.
П р и м е р.
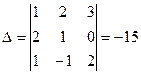 ,
, 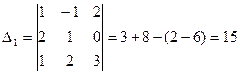 .
.
В 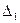 по сравнениюс
по сравнениюс 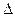 мы поменяли местами первый и третий горизонтальные ряды и показали, что
мы поменяли местами первый и третий горизонтальные ряды и показали, что 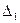 =
= 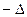 .
.
С л е д с т в и е. Определитель имеющий два одинаковых параллельных ряда равен нулю.
П р и м е р.
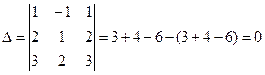 .
.
3. При умножении определителя на число, на это число можно умножить любой ряд определителя.
П р и м е р.
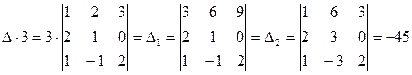 .
.
В случае 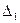 на тройку умножили первый горизонтальный ряд определителя
на тройку умножили первый горизонтальный ряд определителя 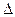 , в случае
, в случае 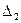 умножали на тройку второй вертикальный ряд.
умножали на тройку второй вертикальный ряд.
Таким образом, сомножитель общий для элементов некоторого ряда определителя можно выносить за знак определителя.
С л е д с т в и я:
1) определитель, содержащий целый ряд нулей равен нулю;
2) определитель, содержащий два пропорциональных параллельных ряда равен нулю.
4. Если элементы некоторого ряда определителя представлены в виде суммы двух (или большего числа) слагаемых, то исходный определитель можно представить в виде суммы двух (или большего числа) определителей.
П р и м е р.
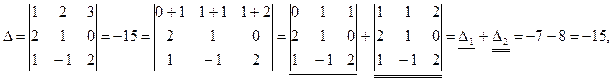 где
где
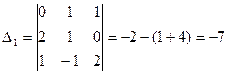 ,
, 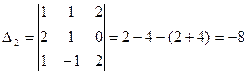 .
.
С л е д с т в и е.Если к элементам некоторого рядаприбавить соответствующие элементы параллельного ряда, предварительно умножив их на одно и то же число, то значение определителя не изменится.
П р и м е р.
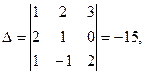
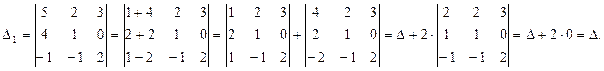 Определитель
Определитель 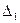 получен путем прибавления к элементам первого столбца определителя
получен путем прибавления к элементам первого столбца определителя 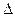 соответствующих элементов второго столбца,
соответствующих элементов второго столбца,
помноженных на два.
Матрицы
Основные определения
Матрицей размерности m 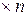 называется прямоугольная таблица элементов, расположенных в m строках и n столбцах:
называется прямоугольная таблица элементов, расположенных в m строках и n столбцах:
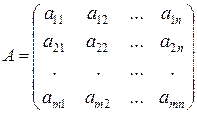 .
.
Элементами матрицы могут быть необязательно числа. Однако в математике нас интересуют, как правило, числовые матрицы.
Если m = 1, то имеем матрицу-строку
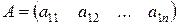 .
.
Если n = 1, то имеем матрицу-столбец
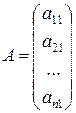 .
.
Если n =т= n, то имеем квадратную матрицу n -го порядка
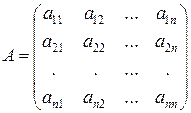 .
.
В квадратной матрице различают элементы 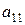 ,
, 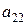 ,...,
,..., 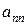 , стоящие на главной диагонали матрицы и элементы
, стоящие на главной диагонали матрицы и элементы 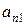 ,
, 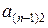 ,...,
,..., 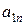 , стоящие на побочной диагонали.
, стоящие на побочной диагонали.
Если в квадратной матрице все элементы, кроме элементов стоящих на главной диагонали, равны нулю, то матрица называется диагональной
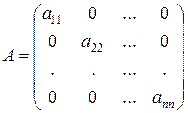 .
.
Если элементы диагональной матрицы, стоящие на главной диагонали, равны единицам, то матрица называется единичной матрицей соответствующего порядка и обозначается через Е:
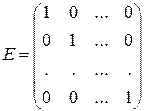 .
.
Две матрицы равны тогда и только тогда, когда они имеют одинаковую размерность и когда в одинаковых ячейках (на одинаковых местах) матриц стоят одинаковые элементы.
Действия с матрицами
Умножение матрицы на число. При умножении матрицы на число, все элементы матрицы множатся на это число
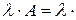
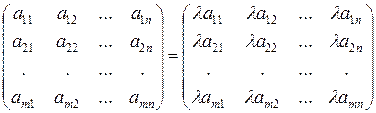 .
.
Таким образом, сомножитель общий для всех элементов матрицы можно выносить за знак матрицы.
Сложение матриц. Складываться могут лишь матрицы одинаковой размерности. При сложении двух матриц одинаковой размерности, складываются их соответствующие элементы
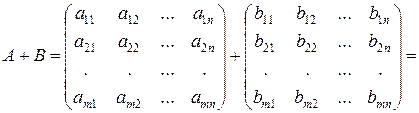
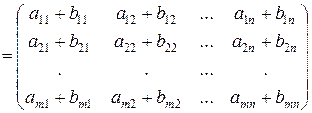 .
.
При вычитании двух матриц одинаковой размерности, из элементов матрицы-уменьшаемого вычитаются соответствующие элементы матрицы-вычитаемого.
Перемножение матриц. Пусть имеем две матрицы A - первая матрица-сомножитель (матрица-множимое) и B - вторая матрица-сомножитель (матрица-множитель). Операция умножения матриц 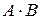 имеет смысл только тогда, когда количество столбцов матрицы-множимого (матрицы А) равно количеству строк матрицы-множителя (матрицы B). В результате умножения двух матриц получаем новую матрицу С, элемент которой
имеет смысл только тогда, когда количество столбцов матрицы-множимого (матрицы А) равно количеству строк матрицы-множителя (матрицы B). В результате умножения двух матриц получаем новую матрицу С, элемент которой 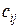 (элемент, стоящий в i – той строке и в j– том столбце матрицы-произведения) получается как результат суммирования произведений элементов i –той строки матрицы А на соответствующие элементы j– того столбца матрицы В, например,
(элемент, стоящий в i – той строке и в j– том столбце матрицы-произведения) получается как результат суммирования произведений элементов i –той строки матрицы А на соответствующие элементы j– того столбца матрицы В, например,
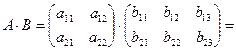
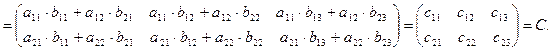
Таким образом, например, 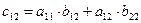 . Матрица А имеет два столбца, матрица В имеет две строки и поэтому их перемножение возможно. Матрица-произведение С содержит столько строк, сколько их имеет матрица-множимое А и столько столбцов сколько их имеет матрица множитель В.
. Матрица А имеет два столбца, матрица В имеет две строки и поэтому их перемножение возможно. Матрица-произведение С содержит столько строк, сколько их имеет матрица-множимое А и столько столбцов сколько их имеет матрица множитель В.
П р и м е р 1.
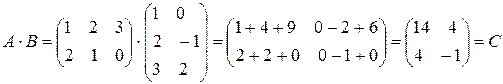 .
.
П р и м е р 2.
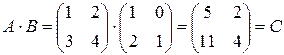 .
.
П р и м е р 3.
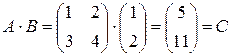 .
.
Обращение матриц. Квадратной матрице 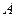 , можно поставить в соответствие ее определитель. Так, например, если матрица имеет вид
, можно поставить в соответствие ее определитель. Так, например, если матрица имеет вид
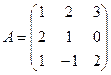 ,
,
то соответствующий ей определитель (детерминант) будет
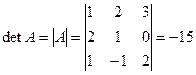 .
.
В случае, если 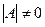 , говорят, что матрица А невырожденная или неособенная, если
, говорят, что матрица А невырожденная или неособенная, если 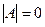 , то А – вырожденная или особенная матрица.
, то А – вырожденная или особенная матрица.
Квадратная матрица 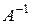 называется обратной по отношению к квадратной матрице А, если их произведение дает единичную матрицу соответствующего порядка
называется обратной по отношению к квадратной матрице А, если их произведение дает единичную матрицу соответствующего порядка 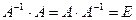 .
.
Необходимое и достаточное условие существования обратной матрицы. Для того чтобы квадратная матрица А имела обратную матрицу необходимо и достаточно, чтобы матрица А была невырожденной.
Схема отыскания обратной матрицы
1. Для квадратной матрицы А находится 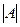 . Убеждаемся, что последний определитель не равен нулю.
. Убеждаемся, что последний определитель не равен нулю.
2. Строится матрица В – матрица алгебраических дополнений членов определителя 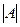 .
.
3. Строится матрица 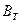 - транспонированная матрица В.
- транспонированная матрица В.
4. Строится матрица 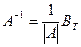 .
.
П р и м е р. Найти обратную матрицу для матрицы
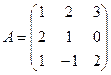 .
.
Р е ш е н и е.
1. 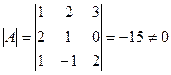 .
.
2. Находим алгебраические дополнения элементов определителя 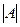 :
:
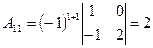 ,
, 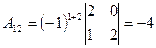 ,
, 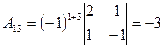 ,
,
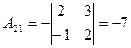 ,
, 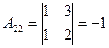 ,
, 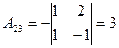 ,
,
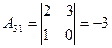 ,
, 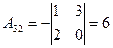 ,
, 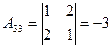 .
.
Теперь
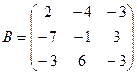 .
.
3. 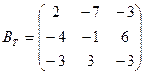 .
.
4. 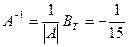
 .
.
П р о в е рк а:
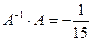
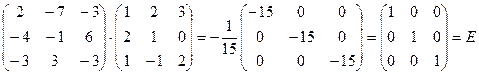 .
.
В результате перемножения А на 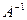 получили единичную матрицу, следовательно обратная матрица найдена верно.
получили единичную матрицу, следовательно обратная матрица найдена верно.
Метод Крамера
Определитель, составленный из коэффициентов при неизвестных системы (1.1) называется главным определителем системы:
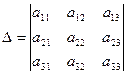 .
.
Теорема Крамера: Если главный определитель системы (1.1) отличен от нуля (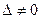 ), то система (1.1) имеет единственное решение. При этом любое неизвестное
), то система (1.1) имеет единственное решение. При этом любое неизвестное 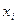 (i = 1, 2, 3) определяется по формуле
(i = 1, 2, 3) определяется по формуле 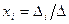 , где
, где 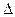 - главный определитель системы,
- главный определитель системы, 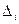 - определитель, получающийся из главного определителя системы путем замены в нем столбца коэффициентов при неизвестной
- определитель, получающийся из главного определителя системы путем замены в нем столбца коэффициентов при неизвестной 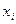 столбцом свободных членов.
столбцом свободных членов.
П р и м е р. С использованием теоремы Крамера (методом Крамера)
решить систему:
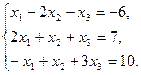
Р е ш е н и е.
Главный определитель системы
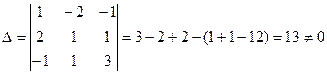 .
.
Вспомогательные определители
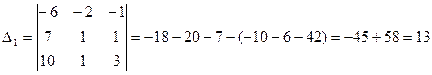 ,
,
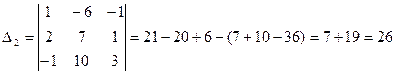 ,
,
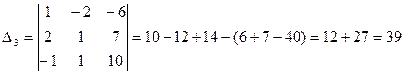 .
.
Теперь 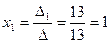 ,
, 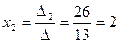 ,
, 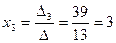 .
.
П р о в е р к а полученного решения
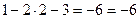 ,
,
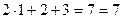 ,
,
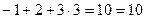 .
.
Все три уравнения при найденном решении 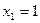 ,
, 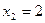 ,
, 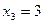 проверились точно. Следовательно, решение верно.
проверились точно. Следовательно, решение верно.
Матричный способ решения
Обозначим
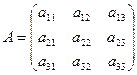 ,
, 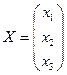 ,
, 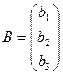 ,
,
где 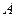 - матрица коэффициентов при неизвестных,
- матрица коэффициентов при неизвестных, 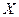 - матрица-столбец неизвестных,
- матрица-столбец неизвестных, 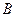 - матрица свободных членов в системе (1.1). Тогда систему (1.1) в матричной форме можно записать в виде
- матрица свободных членов в системе (1.1). Тогда систему (1.1) в матричной форме можно записать в виде
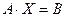 , (1.2)
, (1.2)
поскольку
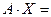
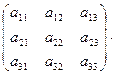
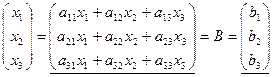 .
.
Из равенства подчеркнутых матриц в цепи следует система (1.1).
Решение матричной системы (1.2) будет
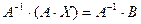
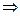
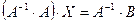
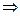
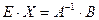
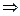
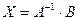 .
.
Таким образом, матрица неизвестных 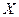 равна произведению матрицы
равна произведению матрицы 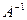 - матрице обратной по отношению к матрице коэффициентов
- матрице обратной по отношению к матрице коэффициентов 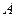 на матрицу свободных членов
на матрицу свободных членов 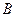 .
.
П р и м е р. Решим матричным способом (с использованием обратной матрицы) систему ранее решенную методом Крамера:
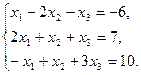
Р е ш е н и е. Для рассматриваемой системы
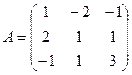 ,
, 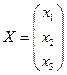 ,
, 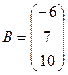 .
.
Строим матрицу 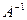 :
:
определитель 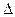 , соответствующий матрице
, соответствующий матрице 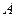 , будет
, будет
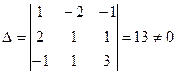 ,
,
алгебраические дополнения элементов определителя 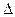 , будут
, будут
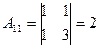 ,
, 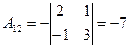 ,
, 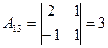 ,
,
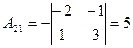 ,
, 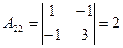 ,
, 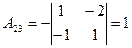 ,
,
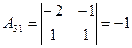 ,
, 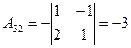 ,
, 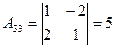 ;
;
матрица 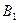 - матрица алгебраических дополнений определителя
- матрица алгебраических дополнений определителя 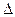
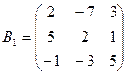 ;
;
матрица
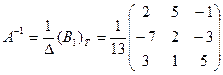 .
.
П р о в е р к а
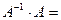
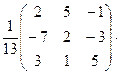
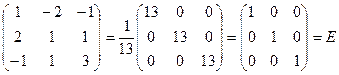 ,
,
обратная матрица найдена, верно.
Теперь
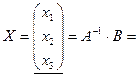
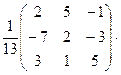
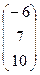 =
= 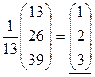 ,
,
из подчеркнутых частей цепи 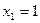 ,
, 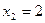 ,
, 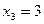 .
.
Векторы и действия с ними
Основные определения
Величина, полностью определяемая своим численным значением, называется скалярной величиной или скаляром.
Величина, определяемая кроме численного значения еще и направлением действия, называется векторной величиной. Схематически вектор – направленный отрезок определенной длины.
 В
В
A
Когда вектор хотят задать точками начала и конца вектора, то вектор обозначают 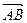 (направление от точки А к точке В), когда достаточно указать, что имеют дело с векторной величиной, то пишут
(направление от точки А к точке В), когда достаточно указать, что имеют дело с векторной величиной, то пишут 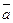 . Длина (модуль) соответствующего вектора обозначается
. Длина (модуль) соответствующего вектора обозначается 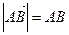 или
или 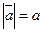 .
.
Векторы называются коллинеарными, если они параллельны одной прямой. Так если два вектора 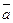 и
и 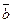 коллинеарные, то пишут
коллинеарные, то пишут 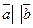
Два вектора 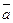
 и
и 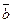 называются равными, если они коллинеарные, равны по длине и одинаково направлены. В этом случае пишут
называются равными, если они коллинеарные, равны по длине и одинаково направлены. В этом случае пишут 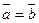 . Если же векторы коллинеарные, равны по длине и направлены в противоположные стороны, то такие векторы называются противоположными, что записывается
. Если же векторы коллинеарные, равны по длине и направлены в противоположные стороны, то такие векторы называются противоположными, что записывается 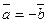 .
.
Векторы называются компланарными, если они параллельны одной плоскости.
В векторной алгебре вводится понятие нулевого вектора – вектора нулевой длины, произвольного направления.
Аффинные координаты
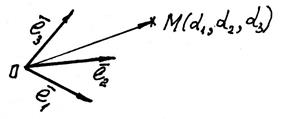
Аффинные координаты в пространстве определяются (рис. 4) заданием базиса
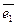
,
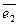
,
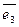
и точки
О – начала координат (
affinis – смежный, соседний).
Рис. 4
Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат: первая – ось абсцисс; вторая – ось ординат; третья – ось аппликат. Плоскости, проходящие через оси координат – координатные плоскости.
Пусть в пространстве задана точка М. 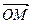 - радиус-вектор точки М. Тогда разложение по векторам базиса
- радиус-вектор точки М. Тогда разложение по векторам базиса 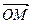 =
= 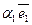 +
+ 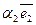 +
+ 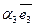 . Аффинными координатами точки М называются координаты - радиус-вектора
. Аффинными координатами точки М называются координаты - радиус-вектора
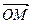 в рассматриваемой системе координат, пишут
в рассматриваемой системе координат, пишут 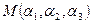 , где
, где 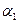 - абсцисса,
- абсцисса, 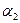 - ордината,
- ордината, 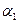 - аппликата точки М. В заданной аффинной системе координат координаты фиксированной точки определяются однозначно. С другой стороны, если задана система координат, то в ней каждой упорядоченной тройке чисел ставится в соответствие единственная точка. Аффинная система координат на плоскости
- аппликата точки М. В заданной аффинной системе координат координаты фиксированной точки определяются однозначно. С другой стороны, если задана система координат, то в ней каждой упорядоченной тройке чисел ставится в соответствие единственная точка. Аффинная система координат на плоскости 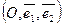 определяет такое же соответствие между точками и упорядоченными парами чисел.
определяет такое же соответствие между точками и упорядоченными парами чисел.
З а д а ч а. Пусть в заданной аффинной системе
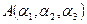
и
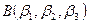
. Требуется найти координаты вектора
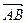
.
Рис. 5
Р е ш е н и е. Из чертежа (рис. 5) видно 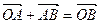 , тогда
, тогда
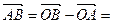
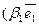 +
+ 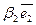 +
+ 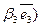
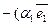 +
+ 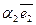 +
+ 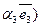 =
=
= 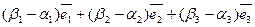 .
.
Таким образом, 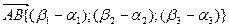 , то есть, координаты вектора равны разности соответствующих координат конца и начала вектора.
, то есть, координаты вектора равны разности соответствующих координат конца и начала вектора.
Проекция вектора на ось
Ориентированной осью называется прямая, на которой закреплена точка - начало отсчета, выбрана единица длины и направление отсчета.
Рис. 6
Проекцией вектора 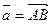 на ось
на ось 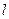
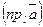 называется величина, численно равная длине отрезка
называется величина, численно равная длине отрезка 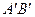 между основаниями перпендикуляров, опущенных из точек А и В на l. Эта длина берется со знаком плюс, если направление от
между основаниями перпендикуляров, опущенных из точек А и В на l. Эта длина берется со знаком плюс, если направление от 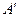 к
к 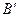 совпадает с направлением оси l и минус в противном случае (рис. 6). Аналогично определяется проекция одного вектора на другой.
совпадает с направлением оси l и минус в противном случае (рис. 6). Аналогично определяется проекция одного вектора на другой.
Углом между осью и вектором называется угол, 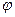 на который нужно повернуть ось до совмещения с вектором кратчайшим образом (так чтобы их стрелки совпали). Из такого определения следует, что
на который нужно повернуть ось до совмещения с вектором кратчайшим образом (так чтобы их стрелки совпали). Из такого определения следует, что 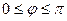 .
.
Свойства проекции вектора на ось.
1.Проекция равна нулю тогда и только тогда, когда вектор перпендикулярен оси (говорят, вектор ортогонален оси).
2. При параллельном переносе вектора его проекция не меняется.
3. Проекция вектора на ось равна произведению длины вектора на
косинус угла между вектором и осью.
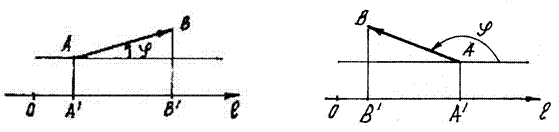
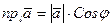 .
.
Рис. 7 Рис. 8
В этой формуле знак проекции регулируется знаком косинуса:
- если 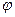 острый угол (рис. 7), то
острый угол (рис. 7), то 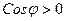 и
и 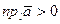 ;
;
- если 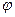 тупой угол (рис. 8), то
тупой угол (рис. 8), то 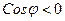 и
и 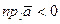 .
.
4. Скалярный множитель можно выносить за знак проекции
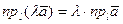 .
.
5. Проекция суммы векторов равна сумме проекций слагаемых
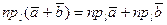 .
.
В.Н.Филатов
ВЫСШАЯ МАТЕМАТИКА
Учебное пособие 1
К изучению курса
для студентов специальности 290800
Саратов – 2005
УДК 512+514+517(075)
ББК 22.11
Ф 51
Рецензенты:
Институт повышения квалификации и переподготовки работников образования (доктор физико-математических наук, профессор В.А.Молчанов)
Доктор физико-математических наук, профессор
Саратовского государственного университета А.И.Землянухин
Одобрено
редакционно-издательским советом
Саратовского государственного технического университета
Филатов В.Н.
Ф 51 Высшая математика: учеб. пособие.
/ В.Н.Филатов. Саратов: Сарат. гос. тех. ун-т, 2005. – 72 с.
ISBN 5-7433-1455-1
В учебном пособии приводятся формулировки теорем, определения, формулы и понятия по линейной и векторной алгебре, аналитической геометрии и введению в анализ - материал, осваиваемый студентами в первом семестре обучения.
Предназначено для методического обеспечения курса вышей математики и может быть полезным при подготовке к практическим занятиям, зачетам, коллоквиумам и экзаменам.
УДК 512+514+517(075)
ББК 22.11
C Саратовский государственный
технический университет, 2005
ISBN 5-7433-1455-1 C Филатов В.Н., 2005
ПРЕДИСЛОВИЕ
Учебное пособие издается в соответствии с постановлением учебно-методической комиссии по специальности «Водоснабжение и водоотведение» (протокол № от июня 2003 г.) и редакционно-издательского совета СГТУ. По мнению УМКС ВиВ в настоящее время по многим дисциплинам интенсивность обучения заметно снизилась. Тому есть много причин:
- недостатки школьного образования;
- возможность поступить на определенные виды образования без конкурсного отбора;
- резкая недостаточность централизованного издания учебников и учебных пособий.
Особенно это присуще обучению студентов на трех начальных курсах. Отмечено, что заметную роль в успешном изучении дисциплины играет быстрота и степень усвоения основных ее понятий. Студенты первых курсов еще не владеют навыками точного переноса понятия или определения в свой конспект, быстрого отыскания их в учебной литературе. Они при подготовке к экзаменам или отчету по модулям затрачивают на это неоправданно много времени.
Цель данного собрания понятий и определений по дисциплине «Высшая математика» заключается в облегчении их поиска, усвоению формулировок и овладением способностью свободной их трактовке и применению. В сборнике помещены рисунки, облегчающие понимание формул и определений. К минимуму в пособии сведено решение примеров, которые также решаются для пояснения определений и свойств математических понятий.
Все замечания и предложения, направленные на улучшение и пополнение учебного пособия будут приняты с благодарностью, обсуждены на заседании УМКС ВиВ и учтены в последующей работе над совершенствованием пособия.
Председатель УМКС ВиВ,
профессор Л.И. Высоцкий
ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРА
1.1. Определители
Основные определения
Определителем второго порядка называется число, которое символически записывается в виде квадратной структуры из четырех элементов (чисел), расположенных в двух строках и двух столбцах:
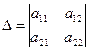 .
.
Здесь числа 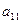 ,
, 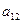 ,
, 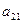 ,
, 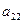 - элементы определителя. Читается, например,
- элементы определителя. Читается, например, 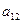 - a один, два (первый индекс указывает на то в какой строке находится рассматриваемый элемент, второй индекс указывает номер столбца в котором находится рассматриваемый элемент).
- a один, два (первый индекс указывает на то в какой строке находится рассматриваемый элемент, второй индекс указывает номер столбца в котором находится рассматриваемый элемент). 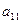 ,
, 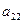 - элементы, стоящие на главной диагонали определителя (диагонали, идущей из левого верхнего угла определителя в нижний правый его угол);
- элементы, стоящие на главной диагонали определителя (диагонали, идущей из левого верхнего угла определителя в нижний правый его угол); 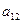 ,
, 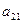 - элементы, стоящие на второй (побочной) диагонали определителя. Определитель второго порядка
- элементы, стоящие на второй (побочной) диагонали определителя. Определитель второго порядка 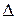 равен разности произведений элементов, стоящих на главной диагонали и на побочной:
равен разности произведений элементов, стоящих на главной диагонали и на побочной:
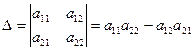 .
.
Определителем третьего порядка называется число, которое символически записывается в виде квадратной структуры из девяти элементов, расположенных в трех строках и трех столбцах и вычисляется по правилу Саррюса
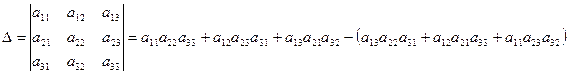 .
.
 Правило Саррюса можно понять из следующих схем, на которых элементы, входящие в одно произведение с указанным знаком, соединены отрезками:
Правило Саррюса можно понять из следующих схем, на которых элементы, входящие в одно произведение с указанным знаком, соединены отрезками:
Аналогично можно дать определение определителей высших порядков, но уже правило вычисления определителя четвертого порядка, типа правила Саррюса, будет трудно понять и запомнить. Позже мы вернемся к вычислению определителей высших порядков. Сейчас же рассмотрим свойства определителей на примере определителей третьего порядка. Эти свойства сохраняют свой вид для определителей любых порядков.
Свойства определителей
Сформулируем свойства и проследим их выполнение на числовых примерах.
1. Определитель не изменит своего значения, если в нем строки заменить соответствующими столбцами. Определитель, в котором строки заменены соответствующими столбцами, называется транспонированным по отношению к исходному определителю.
П р и м е р. Пусть исходный определитель
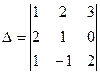 .
.
Тогда транспонированный определитель
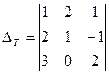 .
.
Первая строка определителя 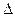 стала первым столбцом определителя
стала первым столбцом определителя 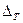 . Первый, второй, третий (слева направо) элементы этой первой строки в
. Первый, второй, третий (слева направо) элементы этой первой строки в 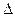 стали соответственно первым, вторым, третьим (сверху вниз) элементами первого столбца в
стали соответственно первым, вторым, третьим (сверху вниз) элементами первого столбца в 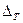 . Аналогично строятся второй и третий столбцы определителя
. Аналогично строятся второй и третий столбцы определителя 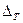 . Определитель
. Определитель 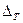 получится из определителя
получится из определителя 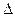 , если элементы определителя
, если элементы определителя 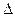 повернуть относительно главной диагонали, как вокруг фиксированной оси, на
повернуть относительно главной диагонали, как вокруг фиксированной оси, на 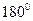 .
.
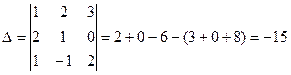 ,
, 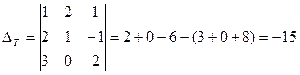 .
.
Таким образом, на примере показали, что 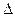 =
= 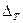 .
.
Из этого первого свойства следует равноправие строк и столбцов в определителе и впредь мы будем их называть рядами.
2. Если в определителе поменять местами два параллельных ряда, то знак определителя изменится на противоположный, абсолютная величина его не изменится.
П р и м е р.
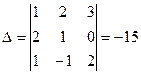 ,
, 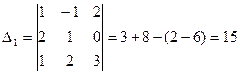 .
.
В 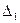 по сравнениюс
по сравнениюс 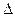 мы поменяли местами первый и третий горизонтальные ряды и показали, что
мы поменяли местами первый и третий горизонтальные ряды и показали, что 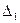 =
= ![]()



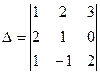 .
.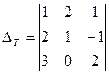 .
.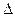 стала первым столбцом определителя
стала первым столбцом определителя 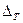 . Первый, второй, третий (слева направо) элементы этой первой строки в
. Первый, второй, третий (слева направо) элементы этой первой строки в 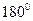 .
.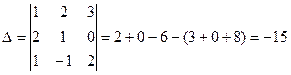 ,
, 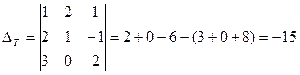 .
.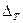 .
.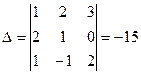 ,
, 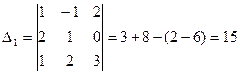 .
.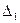 по сравнениюс
по сравнениюс 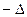 .
.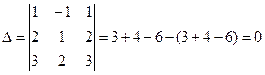 .
.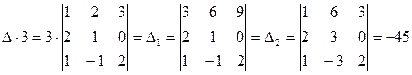 .
.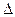 , в случае
, в случае 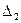 умножали на тройку второй вертикальный ряд.
умножали на тройку второй вертикальный ряд.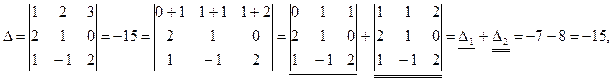 где
где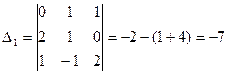 ,
, 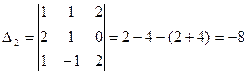 .
.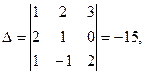
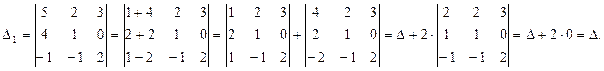 Определитель
Определитель 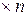 называется прямоугольная таблица элементов, расположенных в m строках и n столбцах:
называется прямоугольная таблица элементов, расположенных в m строках и n столбцах: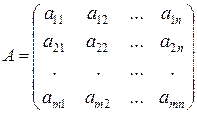 .
. 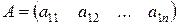 .
.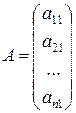 .
.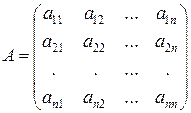 .
.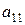 ,
, 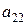 ,...,
,..., 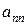 , стоящие на главной диагонали матрицы и элементы
, стоящие на главной диагонали матрицы и элементы 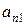 ,
, 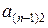 ,...,
,..., 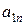 , стоящие на побочной диагонали.
, стоящие на побочной диагонали.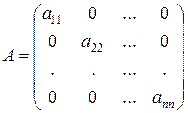 .
.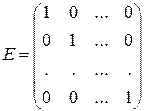 .
.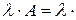
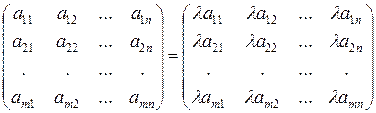 .
.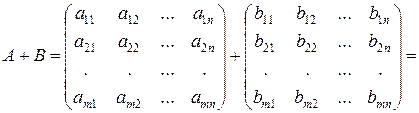
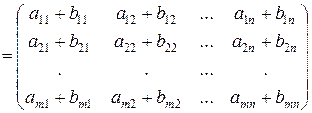 .
.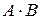 имеет смысл только тогда, когда количество столбцов матрицы-множимого (матрицы А) равно количеству строк матрицы-множителя (матрицы B). В результате умножения двух матриц получаем новую матрицу С, элемент которой
имеет смысл только тогда, когда количество столбцов матрицы-множимого (матрицы А) равно количеству строк матрицы-множителя (матрицы B). В результате умножения двух матриц получаем новую матрицу С, элемент которой 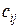 (элемент, стоящий в i – той строке и в j– том столбце матрицы-произведения) получается как результат суммирования произведений элементов i –той строки матрицы А на соответствующие элементы j– того столбца матрицы В, например,
(элемент, стоящий в i – той строке и в j– том столбце матрицы-произведения) получается как результат суммирования произведений элементов i –той строки матрицы А на соответствующие элементы j– того столбца матрицы В, например,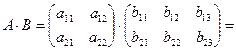
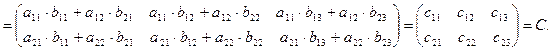
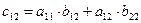 . Матрица А имеет два столбца, матрица В имеет две строки и поэтому их перемножение возможно. Матрица-произведение С содержит столько строк, сколько их имеет матрица-множимое А и столько столбцов сколько их имеет матрица множитель В.
. Матрица А имеет два столбца, матрица В имеет две строки и поэтому их перемножение возможно. Матрица-произведение С содержит столько строк, сколько их имеет матрица-множимое А и столько столбцов сколько их имеет матрица множитель В.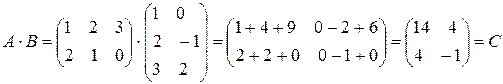 .
.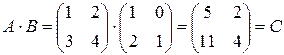 .
.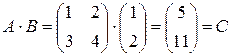 .
.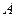 , можно поставить в соответствие ее определитель. Так, например, если матрица имеет вид
, можно поставить в соответствие ее определитель. Так, например, если матрица имеет вид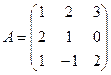 ,
,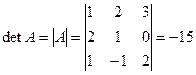 .
.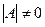 , говорят, что матрица А невырожденная или неособенная, если
, говорят, что матрица А невырожденная или неособенная, если 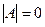 , то А – вырожденная или особенная матрица.
, то А – вырожденная или особенная матрица.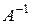 называется обратной по отношению к квадратной матрице А, если их произведение дает единичную матрицу соответствующего порядка
называется обратной по отношению к квадратной матрице А, если их произведение дает единичную матрицу соответствующего порядка 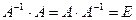 .
.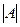 . Убеждаемся, что последний определитель не равен нулю.
. Убеждаемся, что последний определитель не равен нулю.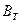 - транспонированная матрица В.
- транспонированная матрица В.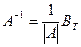 .
.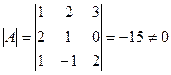 .
.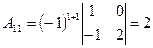 ,
, 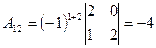 ,
, 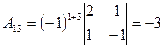 ,
,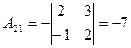 ,
, 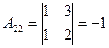 ,
, 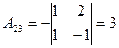 ,
,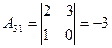 ,
, 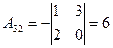 ,
, 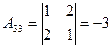 .
.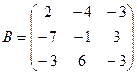 .
.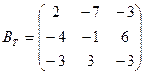 .
.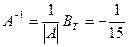
 .
.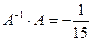
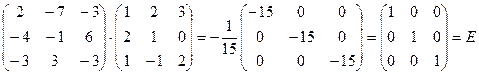 .
.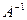 получили единичную матрицу, следовательно обратная матрица найдена верно.
получили единичную матрицу, следовательно обратная матрица найдена верно.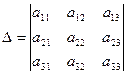 .
.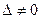 ), то система (1.1) имеет единственное решение. При этом любое неизвестное
), то система (1.1) имеет единственное решение. При этом любое неизвестное 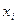 (i = 1, 2, 3) определяется по формуле
(i = 1, 2, 3) определяется по формуле 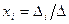 , где
, где 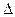 - главный определитель системы,
- главный определитель системы, 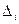 - определитель, получающийся из главного определителя системы путем замены в нем столбца коэффициентов при неизвестной
- определитель, получающийся из главного определителя системы путем замены в нем столбца коэффициентов при неизвестной 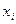 столбцом свободных членов.
столбцом свободных членов.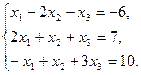
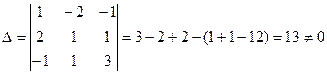 .
.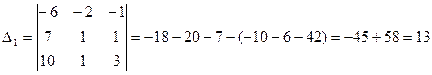 ,
,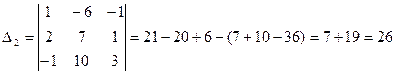 ,
,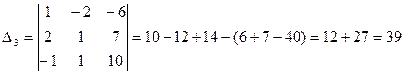 .
.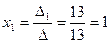 ,
, 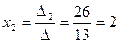 ,
, 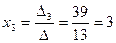 .
.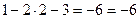 ,
,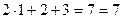 ,
,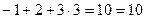 .
.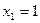 ,
, 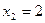 ,
, 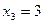 проверились точно. Следовательно, решение верно.
проверились точно. Следовательно, решение верно.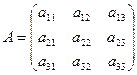 ,
, 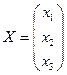 ,
, 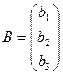 ,
,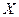 - матрица-столбец неизвестных,
- матрица-столбец неизвестных, 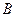 - матрица свободных членов в системе (1.1). Тогда систему (1.1) в матричной форме можно записать в виде
- матрица свободных членов в системе (1.1). Тогда систему (1.1) в матричной форме можно записать в виде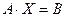 , (1.2)
, (1.2)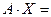
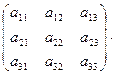
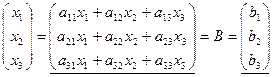 .
.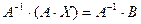
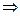
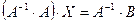
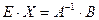
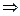
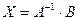 .
.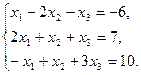
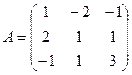 ,
, 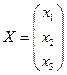 ,
, 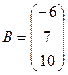 .
.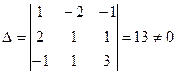 ,
,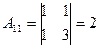 ,
, 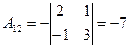 ,
, 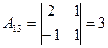 ,
,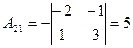 ,
, 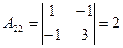 ,
, 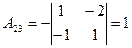 ,
,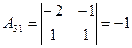 ,
, 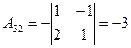 ,
, 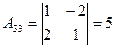 ;
;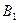 - матрица алгебраических дополнений определителя
- матрица алгебраических дополнений определителя 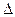
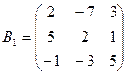 ;
;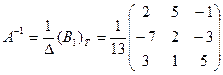 .
.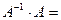
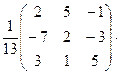
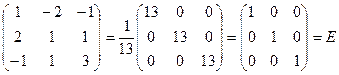 ,
,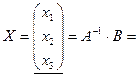
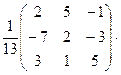
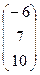 =
= 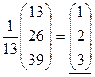 ,
,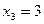 .
. В
В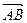 (направление от точки А к точке В), когда достаточно указать, что имеют дело с векторной величиной, то пишут
(направление от точки А к точке В), когда достаточно указать, что имеют дело с векторной величиной, то пишут 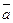 . Длина (модуль) соответствующего вектора обозначается
. Длина (модуль) соответствующего вектора обозначается 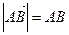 или
или 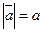 .
.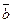 коллинеарные, то пишут
коллинеарные, то пишут 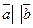
 и
и 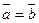 . Если же векторы коллинеарные, равны по длине и направлены в противоположные стороны, то такие векторы называются противоположными, что записывается
. Если же векторы коллинеарные, равны по длине и направлены в противоположные стороны, то такие векторы называются противоположными, что записывается 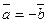 .
.
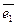 ,
, 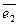 ,
, 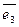 и точки О – начала координат (affinis – смежный, соседний).
и точки О – начала координат (affinis – смежный, соседний).
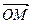 - радиус-вектор точки М. Тогда разложение по векторам базиса
- радиус-вектор точки М. Тогда разложение по векторам базиса 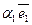 +
+ 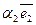 +
+ 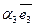 . Аффинными координатами точки М называются координаты - радиус-вектора
. Аффинными координатами точки М называются координаты - радиус-вектора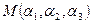 , где
, где 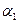 - абсцисса,
- абсцисса, 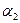 - ордината,
- ордината, 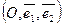 определяет такое же соответствие между точками и упорядоченными парами чисел.
определяет такое же соответствие между точками и упорядоченными парами чисел.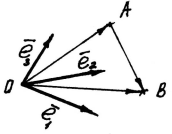
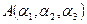 и
и 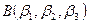 . Требуется найти координаты вектора
. Требуется найти координаты вектора 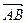 .
.
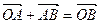 , тогда
, тогда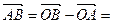
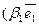 +
+ 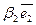 +
+ 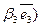
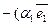 +
+ 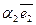 +
+ 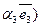 =
=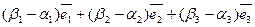 .
.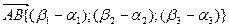 , то есть, координаты вектора равны разности соответствующих координат конца и начала вектора.
, то есть, координаты вектора равны разности соответствующих координат конца и начала вектора.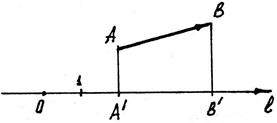
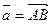 на ось
на ось 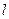
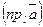 называется величина, численно равная длине отрезка
называется величина, численно равная длине отрезка 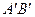 между основаниями перпендикуляров, опущенных из точек А и В на l. Эта длина берется со знаком плюс, если направление от
между основаниями перпендикуляров, опущенных из точек А и В на l. Эта длина берется со знаком плюс, если направление от 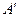 к
к 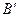 совпадает с направлением оси l и минус в противном случае (рис. 6). Аналогично определяется проекция одного вектора на другой.
совпадает с направлением оси l и минус в противном случае (рис. 6). Аналогично определяется проекция одного вектора на другой.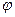 на который нужно повернуть ось до совмещения с вектором кратчайшим образом (так чтобы их стрелки совпали). Из такого определения следует, что
на который нужно повернуть ось до совмещения с вектором кратчайшим образом (так чтобы их стрелки совпали). Из такого определения следует, что 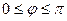 .
.
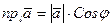 .
.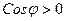 и
и 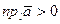 ;
;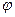 тупой угол (рис. 8), то
тупой угол (рис. 8), то 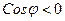 и
и 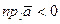 .
.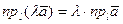 .
.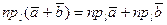 .
.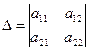 .
.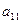 ,
, 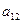 ,
, 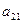 ,
, 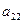 - элементы определителя. Читается, например,
- элементы определителя. Читается, например, 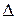 равен разности произведений элементов, стоящих на главной диагонали и на побочной:
равен разности произведений элементов, стоящих на главной диагонали и на побочной: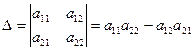 .
.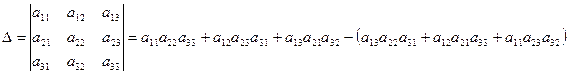 .
. Правило Саррюса можно понять из следующих схем, на которых элементы, входящие в одно произведение с указанным знаком, соединены отрезками:
Правило Саррюса можно понять из следующих схем, на которых элементы, входящие в одно произведение с указанным знаком, соединены отрезками:


