АЛГЕБРА И ГЕОМЕТРИЯ
КОНСПЕКТЫ ЛЕКЦИЙ
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
| Содержание
|
| 1. Уравнения прямой линии на плоскости
| 3
| 1.10. Расстояние от точки до прямой
| 8
|
| 1.1. Общее уравнение прямой
| 3
| 2. Взаимное расположение двух прямых
| 8
|
| 1.2. Неполные уравнения прямой
| 4
| 2.1. Условие параллельности двух прямых, заданных общими уравнениями
| 8
|
| 1.3. Уравнение прямой с угловым коэффициентом
| 4
| 2.2. Условие параллельности двух прямых, заданных с угловыми коэффициентами
| 9
|
| 1.4. Уравнение прямой в «отрезках»
| 5
| 2.3. Условие перпендикулярности двух прямых, заданных общими уравнениями
| 10
|
| 1.5. Каноническое уравнение прямой
| 6
| 2.4. Условие перпендикулярности двух прямых, заданных с угловыми коэффициентами
| 10
|
| 1.6. Уравнение прямой, проходящей через две точки
| 6
| 2.5. Угол между двумя прямыми
| 11
|
| 1.7. Уравнение прямой, проходящей через данную точку параллельно данному направлению
| 6
| 2.6. Угол между двух прямых, заданных с угловыми коэффициентами
| 11
|
| 1.8. Уравнение прямой, проходящей через данную точку перпендикулярно данному направлению
| 7
| 2.7. Угол между двух прямых, заданных общими уравнениями
| 12
|
| 1.9. Нормальное уравнение прямой
| 7
| 2.8. Уравнение пучка прямых
| 12
|
Лекция
Уравнения прямой линии на плоскости. Общее уравнение прямой. Неполные уравнения прямой. Уравнение прямой с угловым коэффициентом. Каноническое уравнение прямой. Уравнение прямой, проходящей через две точки. Уравнение прямой, проходящей через данную точку параллельно данному направлению. Уравнение прямой, проходящей через данную точку перпендикулярно данному направлению. Нормальное уравнение прямой. Расстояние от точки до прямой. Взаимное расположение двух прямых. Условие параллельности двух прямых, заданных общими уравнениями. Условие параллельности двух прямых, заданных с угловыми коэффициентами. Условие перпендикулярности двух прямых, заданных общими уравнениями. Условие перпендикулярности двух прямых, заданных с угловыми коэффициентами. Угол между двух прямых, заданных с угловыми коэффициентами. Угол между двух прямых, заданных общими уравнениями. Уравнение пучка прямых.
Общее уравнение прямой
Линейное уравнение от двух переменных
|
|
|
|
|
|
| 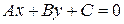 , ,
|
|
|
|
|
| (1)
|
где 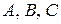 – коэффициенты уравнения, причём
– коэффициенты уравнения, причём 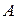 и
и 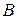 не обращаются в нуль одновременно
не обращаются в нуль одновременно
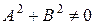 , (2)
, (2)
называется общим уравнением прямой на плоскости.
Любой вектор, перпендикулярный данной прямой, называется нормальным вектором этой прямой. Примером нормального вектора прямой (1) является вектор
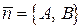 , (3)
, (3)
Любой вектор, параллельный данной прямой, называется направляющим вектором этой прямой. Примером направляющего вектора прямой (1) является вектор
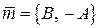 . (4)
. (4)
Это следует из перпендикулярности векторов 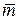 и
и 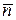 :
: 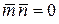 .
.
Неполные уравнения прямой
Если хотя бы один из коэффициентов 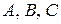 уравнения прямой (1) равен нулю, то оно называется неполным уравнением прямой.
уравнения прямой (1) равен нулю, то оно называется неполным уравнением прямой.
Рассмотрим возможные случаи:
1) 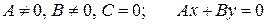 – прямая проходит через начала координат и не совпадает с координатными осями;
– прямая проходит через начала координат и не совпадает с координатными осями;
2) 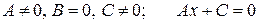 – прямая параллельна оси
– прямая параллельна оси 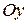 и пересекает ось
и пересекает ось 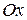 в точке
в точке 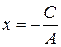 ;
;
3) 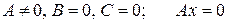 или
или 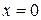 – уравнение координатной оси
– уравнение координатной оси 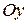 ;
;
4) 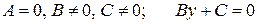 – прямая параллельна оси
– прямая параллельна оси 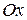 и пересекает ось
и пересекает ось 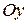 в точке
в точке 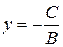 ;
;
5) 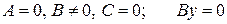 или
или 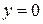 – уравнение координатной оси
– уравнение координатной оси 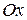 .
.
Если, в общем уравнение прямой (1) все коэффициенты ненулевые, то оно называется полным уравнением прямой.
Нормальное уравнение прямой
Пусть на плоскости 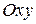 дана прямая
дана прямая 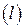 . Отложим от начала координат вектор
. Отложим от начала координат вектор 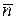 , перпендикулярный данной прямой. Очевидно, что вектор
, перпендикулярный данной прямой. Очевидно, что вектор 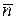 является нормальным вектором прямой
является нормальным вектором прямой 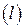 . Длину вектора
. Длину вектора 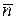 обозначим
обозначим 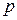
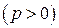 . Угол между этим вектором и осью
. Угол между этим вектором и осью 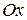 обозначим
обозначим 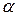 . Тогда уравнение прямой
. Тогда уравнение прямой  может быть записано в виде
может быть записано в виде
|
|
|
|
|
| 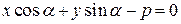 . .
|
|
|
|
| (17)
|
Уравнение (17) называется нормальным уравнением прямой.
Общее уравнение прямой (1) умножением на нормирующий множитель
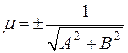 (18)
(18)
приводится к нормальному виду
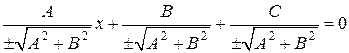 . (19)
. (19)
Из двух знаков выбирается тот, который противоположен знаку 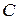 .
.
Заданных общими уравнениями
Если прямые 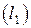 и
и 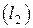 заданы общими уравнениями (22), то условием их перпендикулярности является равенство
заданы общими уравнениями (22), то условием их перпендикулярности является равенство
|
|
|
|
|
|
|
| 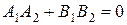 . .
|
|
|
|
|
|
| (31)
|
Действительно, имеем
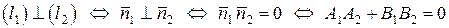 . (32)
. (32)
Угол между двумя прямыми
Пересекающиеся прямые образуют пару вертикальных углов. Меньший из этих вертикальных углов называется углом между прямыми (рис. 2.).
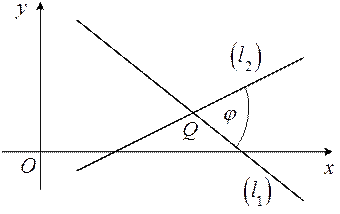
Рис. 2.
Угол между двух прямых,
Угол между двух прямых,
Заданных общими уравнениями
Пусть прямые 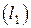 и
и 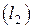 заданы общими уравнениями (27). Так как угловые коэффициенты этих прямых определяются равенствами
заданы общими уравнениями (27). Так как угловые коэффициенты этих прямых определяются равенствами
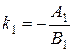 ,
, 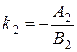 , (38)
, (38)
то нетрудно из равенства (37) вывести формулу
|
|
|
|
|
|
|
| 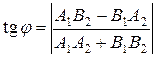 . .
|
|
|
|
|
|
| (39)
|
Если 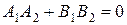 . то имеет место равенство (31) и, следовательно, прямые
. то имеет место равенство (31) и, следовательно, прямые 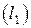 и
и 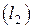 перпендикулярны, а угол между ними прямой.
перпендикулярны, а угол между ними прямой.
Уравнение пучка прямых
Пусть на плоскости 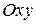 дана некоторая точка
дана некоторая точка 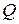 . Совокупность прямых, проходящих через точку
. Совокупность прямых, проходящих через точку 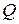 , называется пучком прямых, точка
, называется пучком прямых, точка 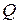 его центром.
его центром.
Уравнения пучка прямых, проходящих через точку 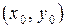 , кроме прямой, параллельной оси
, кроме прямой, параллельной оси 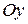 имеют вид
имеют вид
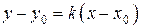 , (40)
, (40)
где 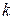 – произвольное вещественное число – угловой коэффициент прямой.
– произвольное вещественное число – угловой коэффициент прямой.
Уравнением пучка прямых, проходящих через точку пересечения двух прямых
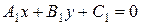 и
и 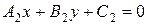 (41)
(41)
является
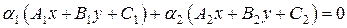 , (42)
, (42)
где 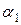 и
и 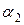 принимают всевозможные вещественные значения.
принимают всевозможные вещественные значения.
АЛГЕБРА И ГЕОМЕТРИЯ
КОНСПЕКТЫ ЛЕКЦИЙ
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
| Содержание
|
| 1. Уравнения прямой линии на плоскости
| 3
| 1.10. Расстояние от точки до прямой
| 8
|
| 1.1. Общее уравнение прямой
| 3
| 2. Взаимное расположение двух прямых
| 8
|
| 1.2. Неполные уравнения прямой
| 4
| 2.1. Условие параллельности двух прямых, заданных общими уравнениями
| 8
|
| 1.3. Уравнение прямой с угловым коэффициентом
| 4
| 2.2. Условие параллельности двух прямых, заданных с угловыми коэффициентами
| 9
|
| 1.4. Уравнение прямой в «отрезках»
| 5
| 2.3. Условие перпендикулярности двух прямых, заданных общими уравнениями
| 10
|
| 1.5. Каноническое уравнение прямой
| 6
| 2.4. Условие перпендикулярности двух прямых, заданных с угловыми коэффициентами
| 10
|
| 1.6. Уравнение прямой, проходящей через две точки
| 6
| 2.5. Угол между двумя прямыми
| 11
|
| 1.7. Уравнение прямой, проходящей через данную точку параллельно данному направлению
| 6
| 2.6. Угол между двух прямых, заданных с угловыми коэффициентами
| 11
|
| 1.8. Уравнение прямой, проходящей через данную точку перпендикулярно данному направлению
| 7
| 2.7. Угол между двух прямых, заданных общими уравнениями
| 12
|
| 1.9. Нормальное уравнение прямой
| 7
| 2.8. Уравнение пучка прямых
| 12
|
Лекция
Уравнения прямой линии на плоскости. Общее уравнение прямой. Неполные уравнения прямой. Уравнение прямой с угловым коэффициентом. Каноническое уравнение прямой. Уравнение прямой, проходящей через две точки. Уравнение прямой, проходящей через данную точку параллельно данному направлению. Уравнение прямой, проходящей через данную точку перпендикулярно данному направлению. Нормальное уравнение прямой. Расстояние от точки до прямой. Взаимное расположение двух прямых. Условие параллельности двух прямых, заданных общими уравнениями. Условие параллельности двух прямых, заданных с угловыми коэффициентами. Условие перпендикулярности двух прямых, заданных общими уравнениями. Условие перпендикулярности двух прямых, заданных с угловыми коэффициентами. Угол между двух прямых, заданных с угловыми коэффициентами. Угол между двух прямых, заданных общими уравнениями. Уравнение пучка прямых.
Уравнения прямой линии на плоскости
Пусть на плоскости задана прямоугольная система координат 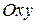 . Положение каждой прямой линии (прямой) на плоскости относительно системы координат
. Положение каждой прямой линии (прямой) на плоскости относительно системы координат 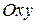 определяется различными способами. Прямая однозначно определяется, если известны:
определяется различными способами. Прямая однозначно определяется, если известны:
1) её угловой коэффициент и отрезок, отсекаемый ею на оси 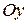 ;
;
2) две точки, через которых она проходит;
3) точка, через которой она проходит параллельно данному направлению;
4) точка, через которой она проходит перпендикулярно данному направлению;
5) два отрезка, отсекаемые ею на координатных осях; и т. д.
В зависимости от способа задания прямой, рассматриваются различные виды ее уравнения.
Отметим, что если речь идёт об уравнении прямой, то имеется в виду, что на плоскости задана прямоугольная система координат 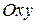 , даже когда это не оговаривается.
, даже когда это не оговаривается.
Общее уравнение прямой
Линейное уравнение от двух переменных
|
|
|
|
|
|
| 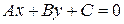 , ,
|
|
|
|
|
| (1)
|
где 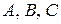 – коэффициенты уравнения, причём
– коэффициенты уравнения, причём 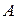 и
и 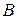 не обращаются в нуль одновременно
не обращаются в нуль одновременно
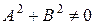 , (2)
, (2)
называется общим уравнением прямой на плоскости.
Любой вектор, перпендикулярный данной прямой, называется нормальным вектором этой прямой. Примером нормального вектора прямой (1) является вектор
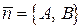 , (3)
, (3)
Любой вектор, параллельный данной прямой, называется направляющим вектором этой прямой. Примером направляющего вектора прямой (1) является вектор
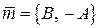 . (4)
. (4)
Это следует из перпендикулярности векторов 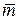 и
и 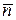 :
: 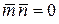 .
.
Неполные уравнения прямой
Если хотя бы один из коэффициентов 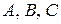 уравнения прямой (1) равен нулю, то оно называется неполным уравнением прямой.
уравнения прямой (1) равен нулю, то оно называется неполным уравнением прямой.
Рассмотрим возможные случаи:
1) 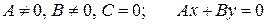 – прямая проходит через начала координат и не совпадает с координатными осями;
– прямая проходит через начала координат и не совпадает с координатными осями;
2) 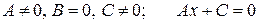 – прямая параллельна оси
– прямая параллельна оси 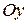 и пересекает ось
и пересекает ось 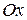 в точке
в точке 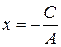 ;
;
3) 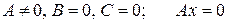 или
или 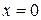 – уравнение координатной оси
– уравнение координатной оси 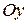 ;
;
4) 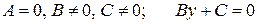 – прямая параллельна оси
– прямая параллельна оси 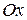 и пересекает ось
и пересекает ось 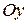 в точке
в точке 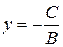 ;
;
5) 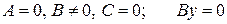 или
или 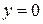 – уравнение координатной оси
– уравнение координатной оси 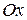 .
.
Если, в общем уравнение прямой (1) все коэффициенты ненулевые, то оно называется полным уравнением прямой.




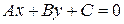 ,
,
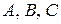 – коэффициенты уравнения, причём
– коэффициенты уравнения, причём 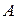 и
и 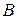 не обращаются в нуль одновременно
не обращаются в нуль одновременно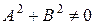 , (2)
, (2)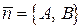 , (3)
, (3)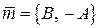 . (4)
. (4)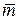 и
и 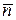 :
: 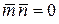 .
.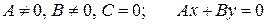 – прямая проходит через начала координат и не совпадает с координатными осями;
– прямая проходит через начала координат и не совпадает с координатными осями;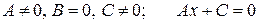 – прямая параллельна оси
– прямая параллельна оси 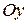 и пересекает ось
и пересекает ось 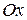 в точке
в точке 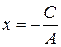 ;
;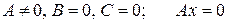 или
или 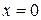 – уравнение координатной оси
– уравнение координатной оси 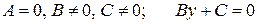 – прямая параллельна оси
– прямая параллельна оси 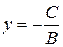 ;
;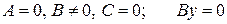 или
или 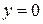 – уравнение координатной оси
– уравнение координатной оси 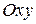 дана прямая
дана прямая 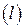 . Отложим от начала координат вектор
. Отложим от начала координат вектор 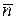 , перпендикулярный данной прямой. Очевидно, что вектор
, перпендикулярный данной прямой. Очевидно, что вектор 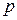
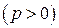 . Угол между этим вектором и осью
. Угол между этим вектором и осью 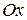 обозначим
обозначим 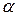 . Тогда уравнение прямой
. Тогда уравнение прямой 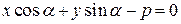 .
.
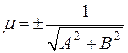 (18)
(18)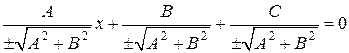 . (19)
. (19)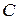 .
.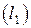 и
и 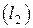 заданы общими уравнениями (22), то условием их перпендикулярности является равенство
заданы общими уравнениями (22), то условием их перпендикулярности является равенство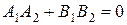 .
.
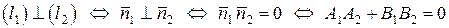 . (32)
. (32)
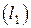 и
и 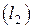 заданы общими уравнениями (27). Так как угловые коэффициенты этих прямых определяются равенствами
заданы общими уравнениями (27). Так как угловые коэффициенты этих прямых определяются равенствами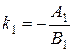 ,
, 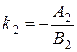 , (38)
, (38)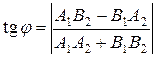 .
.
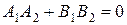 . то имеет место равенство (31) и, следовательно, прямые
. то имеет место равенство (31) и, следовательно, прямые 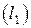 и
и 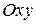 дана некоторая точка
дана некоторая точка 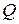 . Совокупность прямых, проходящих через точку
. Совокупность прямых, проходящих через точку 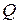 его центром.
его центром.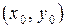 , кроме прямой, параллельной оси
, кроме прямой, параллельной оси 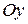 имеют вид
имеют вид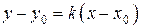 , (40)
, (40)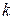 – произвольное вещественное число – угловой коэффициент прямой.
– произвольное вещественное число – угловой коэффициент прямой.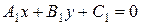 и
и 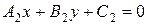 (41)
(41)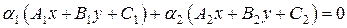 , (42)
, (42)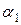 и
и 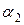 принимают всевозможные вещественные значения.
принимают всевозможные вещественные значения. . Положение каждой прямой линии (прямой) на плоскости относительно системы координат
. Положение каждой прямой линии (прямой) на плоскости относительно системы координат 


