2°. Покажем, как решаются задачи о скоростях и ускорениях, если функция положения известна (составлена). Предположим, что ведущее звено вошло во вращательную кинематическую пару со стойкой. Закон движения его задан зависимостью
φ1 = φ1 (t), тогда его угловая скорость ω1 =  , а угловое ускорение ε1 =
, а угловое ускорение ε1 = 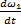 .
.
Линейную скорость υj ведомой точки j или угловую скорость ω j ведомого звена j находят следующим образом:
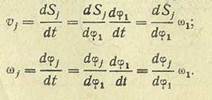
| (20)
(21)
|
Выражение  и
и  называются аналогами скорости или передаточными отношениями. Обозначаем их так:
называются аналогами скорости или передаточными отношениями. Обозначаем их так:
аналог линейной скорости:  или
или  или (υ j)φ1 или i j1;
или (υ j)φ1 или i j1;
аналог угловой скорости:  или φ̍ jφ 1 или (ω j)φ1 или i j1
или φ̍ jφ 1 или (ω j)φ1 или i j1
Линейное касательное ускорение,  ведомой точки ε j или угловое ускорение е. ведомого звена j определяют из выражений:
ведомой точки ε j или угловое ускорение е. ведомого звена j определяют из выражений:

Из формул (20) — (23) видно, что характер изменения скорости и ускорения ведомой точки или ведомого звена механизма зависит от вида функции положения (18) или (19). Численные значения этих параметров определяются конкретными значениями скорости и ускорения ведущего звена.
Из сказанного следует такой порядок аналитического решения задач кинематического анализа механизма.
1. Составляется функция положения.
2. Дифференцированием функции положения находится аналог скорости.
3. Дифференцированием аналога скорости определяется аналог ускорения.
Решим ряд примеров на составление функции положения, попутно найдем выражения для аналогов скорости и ускорения.
Пример 1. Дан синусный механизм (рис. 31). Ведущее звено 1-АВ, его длина lAB — известна, φ1 — координата этого звена, ох — ось отсчета угла φ1 и перемещения S 3 ведомого звена 3.

| Требуется составить функцию положения для звена 3.
Решение. Из треугольника АВК сразу получаем
 аналог скорости
аналог скорости
 аналог ускорения
аналог ускорения

|
Пример 2. Дан тангенсный механизм (рис. 32 ). Ведущее звено 1, расстояние а от центра шарнира А до оси звена 3 известно, φ1 — координата ведущего звена, ох —ось отсчета угла φ1, иперемещения S 3 ведомого звена 3. Требуется составить функцию положения для звена 3.

| Решение. Из треугольника ABK находим.
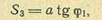 аналог скорости
аналог скорости
 аналог ускорения
аналог ускорения

|
Пример 3. Дана фрикционная Передача с круглыми катками (рис. 33). Радиусы R 1 и R 2 катков известны, φ1 — координата ведущего звена, ох — ось отсчета угла φ1 и угла φ2. Требуется составить функцию положения для звена 2. Положение его определяется углом — φ2 (знак минус указывает, что отсчет этого угла противоположен отсчету угла φ1). Предполагается, что проскальзывание катков одного по другому отсутствует.

Решение. За один и тот же промежуток времени оба катка (1 и 2) повернутся на углы φ1 и φ2, стягиваемые равными дугами S 1 и S 2. Эти дуги равны. S 1 = φ1 R 1; S 2 = φ2 R 2. откуда искомая функция

аналог скорости

аналог ускорения

Для составления выражения функции положения Вяч. А. Зиновьев предложил метод векторных контуров [2].
3°. В том случае, когда выражение для функции положения оказывается громоздким (неудобным для дифференцирования), ее можно построить графически (рис. 34, а ) и её производные (аналоги скорости и ускорения) получить графическим дифференцированием.

Рис. 34. Графики:
а - функции положения; б - первой производной от функции положения.
Пусть график функции положения построен (рис. 34, а) с масштабами по осям координат.
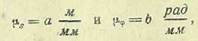
где a и b— некоторые числа.
Аналог скорости
 (24)
(24)
tg αj - тангенс угла αj наклона касательной с осью абсцисс, проведенной к кривой Sj = Sj (φ1) для выбранного угла φ1
Задавшись масштабом аналога скоростей µsj, можно построить его график (рис. 34,6):

ЛЕКЦИЯ ЧЕТВЕРТАЯ
Графический метод.
Метод планов (планы положений, скоростей и ускорений)
1°. Все задачи кинематического анализа методом планов решаются применительно к группам
Ассура, образовавшим механизм. Прежде чем начинать анализ механизма, его следует разложить на группы Ассура. Анализу в первую очередь подлежит группа Ассура, присоединенная к ведущему звену и стойке, т. е. присоединенная первой, и затем надо переходить к группе Ассура, присоединенной во вторую очередь, и т. д.
Методика решения задач анализа специфична для групп Ассура
соответствующего класса.
2°. Планы положений для групп Ассура второго класса. Эта задача для групп второго класса решается методом засечек (с помощью циркуля и линейки). Решение ее покажем на ряде конкретных примеров.
Пример 1. Дан механизм шарнирного четырехзвенника (рис. 35, а). Известны размеры звеньев: 1ав — 0,06 м, 1ВС — 0,18 м, Icd = 0,10 м, Iad — 0,20 м. Положение ведущего звена определяется углом φ1 = 45ᵒ.
Решение. 1) Разделяем механизм на группы Ассура. Это группа — В CD (звенья 2 и 3).
2)Задаемся длиной звена 1, которую удобно отложить на чертеже. АВ = 30 мм. Масштаб
схемы 
3) Определяем длины звеньев, которые следует отложить на чертеже:
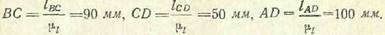
4) Строим на чертеже (рис. 35, б) положение ведущего звена и
Положение центра шарнира D.
5) Строим положение группы Ассура второго класса, первого
вида
Положения центров шарниров В и D построены. Положение центра шарнира С найдется в точке пересечения окружностей радиусов ВС и CD. Решений будет два (точки С и С̍), выбираем то, которое определяется положением С. Это положение соответствует заданной схеме механизма (рис. 35, а). Следует указать, что при аналитическом решении ответов будет четыре, так как две кривые второго порядка имеют четыре точки пересечения. Для нашего случая будут два действительных и два мнимых решения.
Если решить задачу для ряда последовательных значений угла φ1,то мы получим представление о положениях звеньев механизма за определенный интервал движения ведущего звена; обычно исследование ведется для одного кинематического цикла движения механизма. В нашем примере это будет соответствовать одному обороту ведущего звена 1.

Если задача о положениях решена для ряда последовательных положений ведущего звена, то выявляются траектории всех точек, принадлежащих различным звеньям механизма. В частности, определяются траектории точек шатуна, эти траектории носят название шатунных кривых (рис. 35, в). На этом рисунке показана шатунная кривая, построенная для точки М. Шатунная кривая шарнирного четырехзвенника описывается уравнением шестой степени.
Пример 2. Дан кривошипно-шатунный (ползунный) механизм (рис. 36, а). Известны размеры звеньев: lAB = 0,06 м, l ВС = 0,18 м. Положение ведущего звена определяется углом φ1= 45°
Решение. 1) Разделяем механизм на группы Ассура. Этих групп — одна, второго класса, второго вида (она образована звеньями 2 и 3).



2) Задаемся длиной звена 1 — отрезком АВ = 30 мм, масштаб схемы будет µl =  = 0,002
= 0,002 
3) Определяем длины отрезков, которыми будут определяться
размеры звеньев на чертеже: ВС =  = 90 мм.
= 90 мм.
4) Строим на чертеже (рис. 36, б) положения центра шарнира А и направляющей поступательной пары хх.
5) Строим положение группы Ассура второго класса, второго вида.
Положение центра шарнира B и направляющих хх известно. Положение центра шарнира С найдем, если из центра шарнира В проведем окружность радиуса ВС до пересечения с линией хх Решений будет два: С и С', выбираем С, так как оно соответствует заданной схеме (рис. 36, а). На рис. 36, в построена шатунная кривая для точки М, для этого механизма она будет кривой четвертого порядка.
Пример 3. Дана схема механизма строгального станка (рис. 37, а). Известны размеры звеньев механизма: lАВ =0,1 м, lAC = 0,2 м, lCD = 0,3 м, lED = 0,15 м, Н = 0,1 м. Положение ведущего звена 1 определяется углом φ1 = 300°.
Решение. 1) Разделяем механизм на группы Ассура. Этих групп две: группа второго класса, второго вида (звенья 5 и 4) и группа второго класса, третьего вида (звенья 3 и 2).
2) Задаемся длиной отрезка АВ, изображающего на чертеже
звено 1, AB = 25 мм, масштаб схемы µ l =  = 0.004
= 0.004  .
.
3) Определяем длины отрезков, изображающих не схеме остальные размерные параметры:
AC =  = 50 мм, CD =
= 50 мм, CD =  = 0.004 = 75 мм, ED =
= 0.004 = 75 мм, ED =  = 37.5 мм; h =
= 37.5 мм; h =  = 25 мм
= 25 мм
4) Строим на чертеже (рис. 37,6) положения центров шарниров А, С и направляющей хх, а также положение ведущего звена 1.
5) Строим положение группы второго класса, третьего вида (звенья 2 и 3), для чего через центры шарниров С и В проводим прямую Су. Вычерчиваем положение ползуна (камня).
6) Строим положение группы второго класса, второго вида (звенья 4 и 5). Отмечаем на линии Су положение центра шарнира D, из этого центра засечкой радиуса DE находим положение центра шарнира Е на линии хх.
3°. Планы положений для групп Ассура третьего класса. Для этих групп чаще всего применяется метод шаблонов. Пусть дана группа третьего класса BCFEGD (рис. 38, а), положения центров шарниров В, Е, и D известны. Центры шарниров С, G и F должны располагаться, соответственно, на окружностях аа, ββ и γγ- Заготовляя шаблон CGF (рис. 38,6), мы располагаем его на чертеже так, чтобы вершины С, G и F легли бы на соответствующие окружности, тем самым будет решена задача о положениях для группы третьего класса.
Из рассмотрения методов решения задачи о положениях видно, что они различны для групп Ассура разных классов. Они усложняются с повышением номера (разряда) класса.
4°. Планы скоростей (планы аналогов скоростей). Порядок решения задачи о скоростях сохраняется тем же, каким он был при

решении задачи о положениях (механизм разделяется на группы Ассура и анализ начинается с группы Ассура, непосредственно присоединенной к ведущему звену и стойке).
Основные зависимости (10), (12), (14) и (16), которые будут необходимы для решения, даны в третьей лекции. Напомним, что задачу следует считать решенной, если известны скорости двух точек каждого звена механизма или скорости одной точки и угловая скорость звена. В соответствии с этим указанием и надо выбирать необходимые для решения указанные зависимости.
Разницы между планами скоростей и планами их аналогов нет, так как они отличаются только масштабами, поэтому в дальнейшем будет идти речь о планах скоростей. Для получения аналогов скоростей надо будет только пересчитать масштаб построения.
Для большей наглядности решение задачи показано на ряде конкретных примеров.
Пример 1. Дан механизм шарнирного четырехзвенника (рис. 39, а).
Известны: ведущее звено 1, его положение, определяемое углом φ1 и его угловая скорость ω1; размеры звеньев: l AB, l BC, l CD, l AD,

Решение. 1) Разделяем механизм на группы Ассура. В нашем случае одна группа, второго класса, первого вида (звенья 2 и 3).
2) По заданным размерам и положению ведущего звена 1 строим положение механизма (рис. 39, а).
Выбираем необходимые уравнения для решения задачи. Скорости центров шарниров В и D группы нам известны. Если определить скорость центра шарнира С, то задача для группы будет решена. Это вытекает из равенства (10), так как будут известны скорости двух точек каждого звена группы. Искомые урав-нения отвечают формуле (16), написанной для звена 2 и звена 3.
4) План скоростей группы строим по уравнениям типа (16):

где  — скорость (искомая) центра шарнира С:
— скорость (искомая) центра шарнира С:
 —скорость центра шарнира В;
—скорость центра шарнира В;
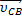 — скорость центра шарнира С при вращении звена 2 около центра шарнира В
— скорость центра шарнира С при вращении звена 2 около центра шарнира В
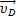 —скорость центра шарнира D (в нашем случае она равна нулю);
—скорость центра шарнира D (в нашем случае она равна нулю);
 — скорость центра шарнира С при вращении звена 3 около центра шарнира D.
— скорость центра шарнира С при вращении звена 3 около центра шарнира D.
Решая совместно векторные равенства, получим план скоростей группы (рис. 39, б).
Отточки р (начала или полюса плана) откладываем отрезок р b, перпендикулярный линии АВ (этот отрезок пропорционален скорости  ), из точки b проводим линию, перпендикулярную линии ВС, — направление скорости υ CB. Это построение отвечает правой части первого равенства. Строим правую часть второго равенства; для этого от точки р откладываем отрезок pd, пропорциональный скорости υD, но она равна нулю, поэтому точка d совпадает с точкой р, из точки d (p) проводим линию, перпендикулярную линии CD, — направление скорости υCD. Пересечение линий, перпендикулярных ВС и CD, даст точку с — конец вектора скорости центра шарнира С — υc Треугольник pbc называется планом скоростей группы, а если в полюс р поместить точку а, отвечающую концу скорости центра шарнира А (эта скорость равна нулю), то эта фигура будет называться планом скоростей механизма.
), из точки b проводим линию, перпендикулярную линии ВС, — направление скорости υ CB. Это построение отвечает правой части первого равенства. Строим правую часть второго равенства; для этого от точки р откладываем отрезок pd, пропорциональный скорости υD, но она равна нулю, поэтому точка d совпадает с точкой р, из точки d (p) проводим линию, перпендикулярную линии CD, — направление скорости υCD. Пересечение линий, перпендикулярных ВС и CD, даст точку с — конец вектора скорости центра шарнира С — υc Треугольник pbc называется планом скоростей группы, а если в полюс р поместить точку а, отвечающую концу скорости центра шарнира А (эта скорость равна нулю), то эта фигура будет называться планом скоростей механизма.
Масштаб плана скоростей
 (25)
(25)
где µ l — масштаб схемы механизма.
Масштаб плана аналогов скоростей
 (26)
(26)
На решенном примере укажем основные свойства плана скоростей.
1) Векторы абсолютных скоростей всех точек механизма имеют своим начало полюс плана p
2) Правило подобия. Концы векторов абсолютных скоростей точек одного звена образуют на плане скоростей фигуру, подобную той, которую одноименные точки образовали на самом звене.
Докажем это правило. Пусть надо найти скорость точки М звена 2 (рис. 39, а). Для этой точки можно записать два равенства типа (16):

где  — скорость точки М при вращении звена 2 около точки B
— скорость точки М при вращении звена 2 около точки B
 — скорость точки М при вращении звена 2 около точки С.
— скорость точки М при вращении звена 2 около точки С.
Решаем эти равенства. Проводим из точки b плана (рис. 39,6) линию, перпендикулярную ВМ, а из точки с — линию, перпендикулярную МС, точка их пересечения даст конец вектора абсолютной скорости точки М, а отрезок рт будет пропорционален этой скорости. Так как линии b с и ВС, bm и ВМ, тс и МС взаимно перпендикулярны, то треугольник b тс подобен треугольнику ВМС. По этому правилу на рис. 39, 6 найдена скорость точки К звена 2. Она найдена из соотношения

Необходимо указать, что получающиеся подобные фигуры на звене и на плане являются сходственно расположенными (чтение их вершин в одном и том же направлении однозначно).
3) Угловые скорости звеньев по плану с учетом формулы (25)
 (27)
(27)
4) План скоростей считается построенным в масштабе кривошипа, если отрезок pb, изображающий вектор скорости ведущей точки В, равен отрезку АВ, изображающему длину этого звена на чертеже, т. е. pb = АВ. В этом случае масштаб плана скоростей
 (28)
(28)
а масштаб плана аналогов скоростей
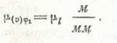 (29)
(29)
5) Повернутыми планами скоростей называются такие, в которых все векторы скоростей повернуты на 90° от своего естественного направления (рис. 39, в). Эти планы содержат меньше графических ошибок и, кроме того, находят применение при решении задач рычагом Жуковского (об этом позже).
Пример 2. Дан кривошипно-шатунный (ползунный) механизм (рис. 40, а). Известны: ведущее звено 1, его положение, определяемое углом φ1 и его угловая скорость ω1; размеры звеньев: l AB,
l ВС.

Решение. 1) Разделяем механизм на группы Ассура. Этих групп — одна, второго класса, второго вида (звенья 2 и 3).
2) По заданным размерам и положению ведущего звена строим положение механизма (рис. 40, а).
3) Выбираем уравнения для решения задачи. Скорость центра шарнира В, а также угловая скорость ω3 звена 3 (она равна нулю) известны. Если по формуле (10) найдем скорость центра шарнира С, то задача будет решена, так как для звена 2 будут известны скорости двух точек, а для звена 3 — скорость одной точки и угловая скорость звена.
4) План скоростей группы строим по уравнению (16):

Решение этого равенства даст план скоростей группы (рис. 40, б). От точки р откладываем отрезок pb, перпендикулярный линии АВ, он пропорционален скорости υB, из точки b проводим линию, перпендикулярную ВС, направление скорости υCB, а из полюса р линию, параллельную хх, направление скорости центра шарнира С. Точка пересечения с этих линий даст конец вектора искомой скорости υ c, а отрезок рс будет ей пропорционален. Помещаем в полюс точку а и тем самым получаем план скоростей всего механизма. Масштабы планов скоростей и их аналогов найдем по формулам (25) и (26)
Пример 3. Дан кулисный механизм Витворта (рис. 41, а). Известны: ведущее звено 1, его положение, определяемое углом φ1 и его угловая скорость ω1 размеры звеньев l AB, l AC.

Решение. 1) Разделяем механизм на группы Ассура. Из этих групп берем одну второго класса, третьего вида (звенья 2 и 3).
2) По заданному положению ведущего звена и заданным размерам строим положение механизма (рис. 41, а).
3) Выбираем уравнения для решения. Скорость центра шарнира В известна. Угловые скорости звеньев 2 и 3 одинаковы (неизвестны), следует найти скорость точки Б3, лежащей под центром шарнира В. В этом случае будут известны скорости двух точек звена 3 (точки В3 и центра шарнира С), а для звена 2 скорость центра шарнира В известна, угловую скорость ω2, равную угловой скорости звена 3, определяем из плана скоростей по формуле типа (27).
4) План скоростей группы строим по уравнению (14). Решение его даст искомый план скоростей группы (рис. 41,6):
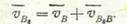
От точки р отложим отрезок pb, перпендикулярный линии AB, скорость υ B, из точки b проведем линию, параллельную линии Су, направление скорости υ B 3 B а из полюса p проведем линию
, перпендикулярную Су,, направление скорости υ B 3 (точнее направление скорости υ B 3 C, но так как центр шарнира С неподвижен, то υ B 3 = υ B 3 C). В точке пересечения этих линий найдем точку b 3 — конец вектора скорости точки В3. Поместим точку а в полюс плана и окончательно получим план скоростей механизма. Угловая скорость звена 3
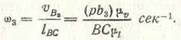
Масштабы планов найдем по формулам (25) и (26).
Пример 4. Дан кривошипный механизм с качающимся, ползуном (рис. 42, а). Известны: ведущее звено 1, его положение, определяемое углом φ1 и его угловая скорость ω1; размеры звеньев: l AB, l AC.

Решение. 1) Разделяем механизм на группы Ассура. Этих групп — одна, второго класса, третьего вида.
2) По заданным размерам и положению ведущего звена строим положение механизма (рис. 42, а).
3) Выбираем уравнения для решения задачи. Скорости центров шарниров В и С известны (скорость υ С = 0). Угловые скорости звеньев 2 и 3 равны между собою (неизвестны). Задачу решим, если найдем скорость точки С 2, звена 2, лежащей под центром шарнира С. Для звена 2 будем знать скорость двух точек: центра шарнира В — υB и точки С2 — υc 2, а для звена 3 скорость центра шарнира С известна и равна нулю (vc3 = 0). Угловую скорость его найдем из плана скоростей.
4) План скоростей группы строим по уравнениям типа (16) и (14) (рис. 42,6).

От точки р откладываем отрезок pb, перпендикулярный линии АВ, скорость υB, из точки b проводим линию, перпендикулярную линии ВС, направление скорости υC 2 B. От точки р следовало бы отложить отрезок рс3 — скорость центра шарнира С, но она равна нулю, поэтому точку с3 совмещаем с полюсом р. Из точки с3(р) проводим направление скорости υC 2 C 3 параллельно линии ВС, пересечение ее с линией, проведенной через точку b, даст точку с2 — конец вектора скорости точки С 2. В полюсе помещаем точку а — план скоростей механизма построен. Масштабы найдем по формулам (25) и (26). Угловая скорость звена 3

5°. Задачи о положениях и скоростях для кулачковых механизмов. Задача о положениях решается методом обращения движения (рис. 43). Сообщаем мысленно всему механизму угловую скорость,

равную угловой скорости кулачка, но противоположной ей по знаку. Теперь кулачок 1 остановится, а стойка 3 и штанга 2 будут двигаться с угловой скоростью ω1. Относительная линейная скорость штанги относительно стойки сохранит свое значение. Пусть кулачок повернется на угол φ1. Надо определить перемещение штанги, соответствующее этому углу поворота. Начальное положение штанги определяется линией А у и конец штанги В2 лежит на профиле кулачка 1. При повороте кулачка на угол φ1 линия Ау в относительном движении повернется на угол — φ1 и займет положение Ау', а конец штанги займет положение В2̍. Проведя окружность радиуса АВ2̍, найдем положение конца штанги при повороте кулачка на угол φ1 Это положение обозначено В2". Перемещение штанги соответственно будет равно В2В2".
Задачу о скоростях для этих механизмов можно решать двояко: либо, предварительно построив заменяющий механизм, строить планы для соответствующих групп Ассура, либо решить уравнение типа (14).
На рис. 44, а показан кулачковый механизм. Уравнение типа (14) для него будет
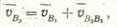
где  —скорость точки B 1 принадлежащей кулачку;
—скорость точки B 1 принадлежащей кулачку;
 —скорость точки В2, принадлежащей штанге и совпадающей с точкой В1 кулачка;
—скорость точки В2, принадлежащей штанге и совпадающей с точкой В1 кулачка;
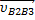 — скорость скольжения точки В2 штанги относительно точки B 1 кулачка.
— скорость скольжения точки В2 штанги относительно точки B 1 кулачка.
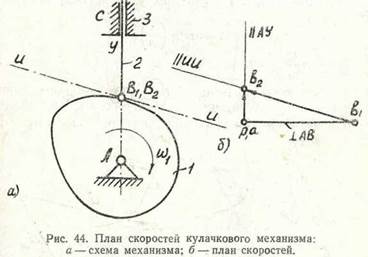
Она направлена параллельно линии ии, касательной к профилю кулачка.
План скоростей изображен на рис. 44, б. От точки р отложим отрезок pb 1 перпендикулярный АВ — вектор скорости υB 1; через точку b 1 проведем направление скорости υB 2 B 1 —линию, параллельную ии, а из полюса р линию, параллельную Ау, — направление скорости υB 2. В пересечении этих линий найдем точку b 2 — конец вектора скорости точки υB 2. План скоростей построен. Масштаб его найдем по формулам (25) и (26).
Во избежание ошибок планы ускорений следует строить для заменяющего махенизм
ЛЕКЦИЯ ПЯТАЯ
(Продолжение четвертой лекции)
6°. Планы ускорений (планы аналогов ускорений).
Задача об ускорениях решается в той же последовательности, что и задача о скоростях. Ее решение будет основываться на соотношениях типа (11), (15) и (17). Основные свойства планов ускорений будут аналогичны основным свойствам планов скоростей.
Эти свойства следующие.
1) Векторы абсолютных ускорений всех точек механизма имеют
своим началом полюс (начало) плана π.
2) Правило подобия. Концы векторов абсолютных ускорений точек одного звена образуют на плане ускорений фигуру, подобную той, которую одноименные точки образовали на самом звене.
Замечание. В планах скоростей стороны подобных фигур составляют угол 90˚ (обычные планы) или параллельны (повернутые планы). В планах же ускорений эти стороны наклонены одна к другой под углом δ, который определяется формулой
 (30)
(30)
ε—- угловое ускорение звена:
ω — угловая скорость его.
На рис. 45, а показано звено ВСМ, вращающееся с угловой скоростью ω и угловым ускорением ε, а на рис. 45, б построен план ускорений этого звена. Так как модули векторов  и
и  пропор
пропор

циональны расстояниям ВС и ВМ, то треугольники ВМС и bm с подобны.
3) Угловые ускорения звеньев
ε = 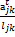 (31)
(31)
здесь ε — угловое ускорение звена;
ajk — касательное ускорение точки j при вращении звена относительно точки k;
l jk - расстояние между точками j и k
4) Масштабы планов ускорений и их аналогов связаны соотношением:
 (32)
(32)
где µ a — масштаб плана ускорений;
µ( a ) φ1— масштаб плана аналогов ускорений;
ω1 — угловая скорость ведущего звена.
Построение планов ускорений для групп Ассура второго класса проследим на примерах построения их для отдельных механизмов. Будем считать, что для всех механизмов известны: размерные параметры, ведущее звено (ему будем приписывать номер один), положение ведущего звена (оно задано углом φ1), угловая скорость ω1 ведущего звена (она считается постоянной). Кроме того, для этих механизмов задачи о положениях и скоростях решены.
Пример 1. Дан механизм шарнирного четырехзвенника (рис. 46, а). Этот механизм образован присоединением к ведущему звену 1 группы Ассура второго класса, первого вида (звенья 2 и 3)

Решение. Задача о положениях решена (рис. 46, а), также решена задача о скоростях: построен план скоростей (рис. 46, б)
Строим план ускорений. Ускорение центра шарнира В, аВ = 
и направлено параллельно ВА, ускорение центра шарнира D равно нулю: aD =0. Имея в виду соотношение (11), можно утверждать, что, определив ускорение центра шарнира С, решим задачу об ускорениях для группы BCD (так как мы будем знать ускорения двух точек каждого звена группы).
Напишем формулу типа (17) для звена 2 и звена 3:

где  —ускорение центра шарнира С;
—ускорение центра шарнира С;
 — нормальное ускорение центра шарнира В, оно же будет» и полным ускорением его, так как звено 1 вращается; равномерно;
— нормальное ускорение центра шарнира В, оно же будет» и полным ускорением его, так как звено 1 вращается; равномерно;
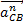 — нормальное ускорение центра шарнира С при вращении
— нормальное ускорение центра шарнира С при вращении
звена 2 около центра шарнира В, a n CB = 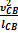 и направлено
и направлено
параллельно линии СВ от С к В;
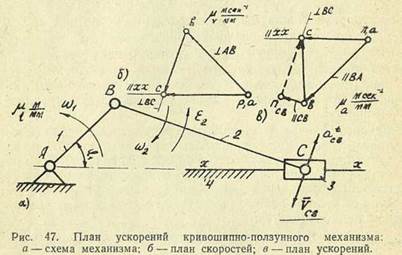
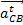 — касательное (тангенциальное) ускорение центра шарнира С, а t CB = ε2 lBC и направлено перпендикулярно линии ВС;
— касательное (тангенциальное) ускорение центра шарнира С, а t CB = ε2 lBC и направлено перпендикулярно линии ВС;
 —ускорение центра шарнира D, оно равно нулю;
—ускорение центра шарнира D, оно равно нулю;
 — нормальное ускорение центра шарнира С при вращении
— нормальное ускорение центра шарнира С при вращении
звена 3 около центра шарнира D, a nCD =  и направлено параллельно линии CD от С к D;
и направлено параллельно линии CD от С к D;
 — касательное ускорение центра шарнира С при вращении звена 3 около центра шарнира D, atCD = ε3 l CD и направлено перпендикулярно линии CD.
— касательное ускорение центра шарнира С при вращении звена 3 около центра шарнира D, atCD = ε3 l CD и направлено перпендикулярно линии CD.
Совместное решение двух равенств типа (17) и даст искомый план. От точки π начала плана откладываем отрезок π b (рис. 46, в), параллельный линии BA, он пропорционален ускорению aB
Масштаб плана ускорений
 (33)
(33)
Вычисляем длину отрезка b п св, изображающего в плане ускорение а n CB,
 (34)
(34)
и откладываем его от точки b — конца вектора a B,
параллельно линии СВ: через точку nCB проводим линию, перпендикулярную линий СВ, — направление ускорения а t CB. Теперь строим правую часть второго равенства.
От точки π следует отложить ускорение а D, оно равно нулю, поэтому конец его d совмещаем с точкой π (полюсом плана). От точки d отложим отрезок dnCD, величину которого найдем по формуле (34): dnCD =  , через точку n CD проводим линию, перпендикулярную линии CD,— направление ускорения а t CD. Пересечение этой линии с ранее проведенной через точку п CB даст точку с — конец вектора искомого ускорения центра шарнира С, а сам вектор определится, если соединить точки π и с. Соединив точки b и с, получим вектор полного ускорения центра шарнира С, которое у него будет при вращении звена 2 около центра шарнира В, — ускорение а CB.
, через точку n CD проводим линию, перпендикулярную линии CD,— направление ускорения а t CD. Пересечение этой линии с ранее проведенной через точку п CB даст точку с — конец вектора искомого ускорения центра шарнира С, а сам вектор определится, если соединить точки π и с. Соединив точки b и с, получим вектор полного ускорения центра шарнира С, которое у него будет при вращении звена 2 около центра шарнира В, — ускорение а CB.
Ускорение точки М звена 2 найдем, если на стороне b с в плане построим треугольник b ст, подобный треугольнику ВСМ на звене 2. Стороны треугольника b ст легко определить графически. Для этого на стороне ВС (рис. 46, а) отложим отрезок b с, равный отрезку b с на плане. Проведя через точку с линию, параллельную СМ до пересечения со стороной ВМ, найдем точку т, тем самым и длины всех сторон треугольника b тс.
Угловое ускорение звена 2 определим по формуле (31):

аналогично может быть найдено угловое ускорение звена 3.
Совместив точку а с точкой π, получим не только план ускорений группы, но и план ускорений всего механизма.
В заключение укажем, что при построении планов в масштабе кривошипа значительно сокращаются все вычислительные операции. Так, если р b = АВ (на плане скоростей) и π b = АВ (на плане ускорений), то масштабы планов

Тогда, например, отрезок bпCB будет определяться так

Отсюда надо запомнить правило для нахождения отрезков в плане ускорений (при условии, что планы скоростей, и ускорений построены в масштабе кривошипа): в формулы, по которым определяются те или иные ускорения, следует вставлять не значения скоростей и длин, а отрезки из плана скоростей и плана положений, которые замеряются по чертежу. Если эти отрезки измерены в миллиметрах, то и отрезок, изображающий соответствующее ускорение, будет измеряться в миллиметрах.
Пример 2. Дан кривошипно-шатунный (ползунный) механизм (рис. 47, а). Этот механизм образован присоединением к ведущему звену 1 группы Ассура второго класса, второго вида (звенья 2 и 3).
Решение. Задача о положениях решена (рис. 47, а), также решена задача о скоростях: построен план скоростей (рис. 47,6). Строим план ускорений. Ускорение центра шарнира
В известно: a B =  , направлено параллельно линии ВА. Угловое ускорение звена 3 равно нулю. Имея в виду соотношение (11), можно утверждать, что, определив ускорение центра шарнира С, мы решим задачу об ускорениях для группы, состоящей из звеньев 2 и 3 (так как мы будем знать для звена 2 ускорения двух точек, а для звена 3 — ускорение одной точки и угловое ускорение звена). •
, направлено параллельно линии ВА. Угловое ускорение звена 3 равно нулю. Имея в виду соотношение (11), можно утверждать, что, определив ускорение центра шарнира С, мы решим задачу об ускорениях для группы, состоящей из звеньев 2 и 3 (так как мы будем знать для звена 2 ускорения двух точек, а для звена 3 — ускорение одной точки и угловое ускорение звена). •
Напишем формулу типа (17) для звена 2:

где ас —ускорение центра шарнира С, его величина неизвестна, а направлено оно параллельно линии хх;
а в— ускорение центра шарнира В, ав=  и направлено
и направлено
параллельно линии ВА от В к А
anCB - нормальное ускорение



 , а угловое ускорение ε1 =
, а угловое ускорение ε1 = 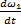 .
.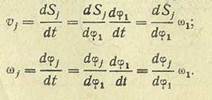
 и
и  называются аналогами скорости или передаточными отношениями. Обозначаем их так:
называются аналогами скорости или передаточными отношениями. Обозначаем их так: или (υ j)φ1 или i j1;
или (υ j)φ1 или i j1; ведомой точки ε j или угловое ускорение е. ведомого звена j определяют из выражений:
ведомой точки ε j или угловое ускорение е. ведомого звена j определяют из выражений:

 аналог скорости
аналог скорости
 аналог ускорения
аналог ускорения


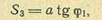 аналог скорости
аналог скорости
 аналог ускорения
аналог ускорения






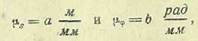
 (24)
(24)

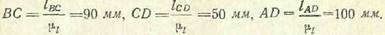




 = 0,002
= 0,002 
 = 90 мм.
= 90 мм. = 0.004
= 0.004  .
. = 50 мм, CD =
= 50 мм, CD =  = 0.004 = 75 мм, ED =
= 0.004 = 75 мм, ED =  = 37.5 мм; h =
= 37.5 мм; h =  = 25 мм
= 25 мм


 — скорость (искомая) центра шарнира С:
— скорость (искомая) центра шарнира С: —скорость центра шарнира В;
—скорость центра шарнира В;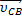 — скорость центра шарнира С при вращении звена 2 около центра шарнира В
— скорость центра шарнира С при вращении звена 2 около центра шарнира В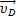 —скорость центра шарнира D (в нашем случае она равна нулю);
—скорость центра шарнира D (в нашем случае она равна нулю); — скорость центра шарнира С при вращении звена 3 около центра шарнира D.
— скорость центра шарнира С при вращении звена 3 около центра шарнира D. (25)
(25) (26)
(26)
 — скорость точки М при вращении звена 2 около точки B
— скорость точки М при вращении звена 2 около точки B — скорость точки М при вращении звена 2 около точки С.
— скорость точки М при вращении звена 2 около точки С.
 (27)
(27) (28)
(28)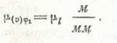 (29)
(29)


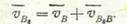
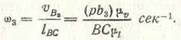




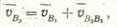
 —скорость точки B 1 принадлежащей кулачку;
—скорость точки B 1 принадлежащей кулачку; —скорость точки В2, принадлежащей штанге и совпадающей с точкой В1 кулачка;
—скорость точки В2, принадлежащей штанге и совпадающей с точкой В1 кулачка;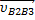 — скорость скольжения точки В2 штанги относительно точки B 1 кулачка.
— скорость скольжения точки В2 штанги относительно точки B 1 кулачка.
 (30)
(30) и
и  пропор
пропор
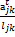 (31)
(31) (32)
(32)


 —ускорение центра шарнира С;
—ускорение центра шарнира С; — нормальное ускорение центра шарнира В, оно же будет» и полным ускорением его, так как звено 1 вращается; равномерно;
— нормальное ускорение центра шарнира В, оно же будет» и полным ускорением его, так как звено 1 вращается; равномерно;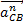 — нормальное ускорение центра шарнира С при вращении
— нормальное ускорение центра шарнира С при вращении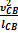 и направлено
и направлено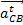 — касательное (тангенциальное) ускорение центра шарнира С, а t CB = ε2 lBC и направлено перпендикулярно линии ВС;
— касательное (тангенциальное) ускорение центра шарнира С, а t CB = ε2 lBC и направлено перпендикулярно линии ВС; —ускорение центра шарнира D, оно равно нулю;
—ускорение центра шарнира D, оно равно нулю; — нормальное ускорение центра шарнира С при вращении
— нормальное ускорение центра шарнира С при вращении и направлено параллельно линии CD от С к D;
и направлено параллельно линии CD от С к D; — касательное ускорение центра шарнира С при вращении звена 3 около центра шарнира D, atCD = ε3 l CD и направлено перпендикулярно линии CD.
— касательное ускорение центра шарнира С при вращении звена 3 около центра шарнира D, atCD = ε3 l CD и направлено перпендикулярно линии CD. (33)
(33) (34)
(34) , через точку n CD проводим линию, перпендикулярную линии CD,— направление ускорения а t CD. Пересечение этой линии с ранее проведенной через точку п CB даст точку с — конец вектора искомого ускорения центра шарнира С, а сам вектор определится, если соединить точки π и с. Соединив точки b и с, получим вектор полного ускорения центра шарнира С, которое у него будет при вращении звена 2 около центра шарнира В, — ускорение а CB.
, через точку n CD проводим линию, перпендикулярную линии CD,— направление ускорения а t CD. Пересечение этой линии с ранее проведенной через точку п CB даст точку с — конец вектора искомого ускорения центра шарнира С, а сам вектор определится, если соединить точки π и с. Соединив точки b и с, получим вектор полного ускорения центра шарнира С, которое у него будет при вращении звена 2 около центра шарнира В, — ускорение а CB.




 и направлено
и направлено


