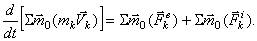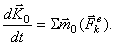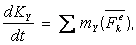Вопрос Условия равновесия произвольной плоской системы сил
Для равновесия любой плоской системы сил необходимо и достаточно, чтобы выполнялись условия (4.2.5):
Записывая условия равновесия в аналитической форме, можно привести три их классических вида:
1. Основная форма условий равновесия:
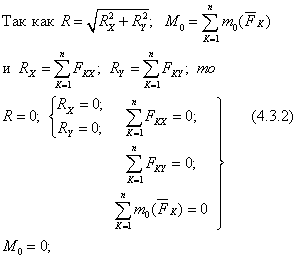
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций на оси координат были равны нулю и сумма моментов всех сил относительно центра О была равна нулю.
2. Вторая форма условий равновесия.
Для равновесия произвольной плоской системы необходимо и достаточно, чтобы сумма моментов относительно двух произвольно взятых точек тела была равна нулю и сумма проекций сил на одну из осей координат была равна нулю:
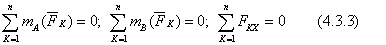
3. Уравнения трех моментов.
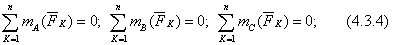
Дополнительное условие: А, В, С не лежат на одной прямой.
Вопрос 6
Теорема Вариньона о моменте равнодействующей относительно оси
Данная теорема формулируется совершенно аналогичным образом как и для плоской системы в разделе 3.7.
Теорема: если данная система имеет равнодействующую, то момент этой равнодействующей относительно любой оси равен алгебраической сумме моментов слагаемых сил относительно той же оси.
Пусть на тело действует система сил 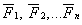 (рис.35
(рис.35  )
)
Пусть эта система приводится к равнодействующей, проходящей через точку С. Приложив в этой точке силу 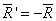 мы приведем систему сил
мы приведем систему сил 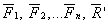 в равновесие и для нее будут выполняться условия (5.3.2). В частности для оси Ох:
в равновесие и для нее будут выполняться условия (5.3.2). В частности для оси Ох:
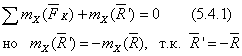
Сделав замену в (5.4.1) получаем:
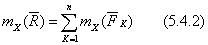
что и требовалось доказать.
Вопрос 7. Кинематические характеристики вращательного движения точки
Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами.
Теорема о проекциях векторов скоростей напрямую, соед. их начало.
Теорема о проекциях скоростей двух точек тела
Определение скоростей точек плоской фигуры (или тела, движущегося плоскопараллельно) связано обычно с довольно сложными расчетами. Однако можно получить ряд других, практически более удобных и простых методов определения скоростей точек фигуры (или тела).
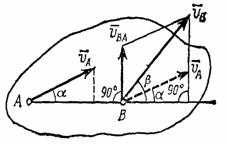
Рис.32
Один из таких методов дает теорема: проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу. Рассмотрим какие-нибудь две точки А и В плоской фигуры (или тела). Принимая точку А за полюс (рис.32), получаем 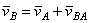 . Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор
. Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор 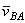 перпендикулярен АВ, находим
перпендикулярен АВ, находим
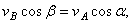
и теорема доказана.
Рис.48
Рассмотрим точку М, движущуюся по отношению к подвижно системе отсчета Oxyz, которая в свою очередь как-то движется относительно другой системы отсчета 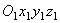 , которую называем основной или условно неподвижной (рис. 48). Каждая из этих систем отсчета связана, конечно, с определенным телом, на чертеже не показанным. Введем следующие определения.
, которую называем основной или условно неподвижной (рис. 48). Каждая из этих систем отсчета связана, конечно, с определенным телом, на чертеже не показанным. Введем следующие определения.
1. Движение, совершаемое точкой М по отношению к подвижной системе отсчета (к осям Oxyz), называется относительным движением (такое движение будет видеть наблюдатель, связанный с этими осями и перемещающийся вместе с ними). Траектория АВ, описываемая точкой в относительном движении, называется относительной траекторией. Скорость точки М по отношению к осям Oxyz называется относительной скоростью (обозначается 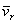 ), a ускорение - относительным ускорением (обозначается
), a ускорение - относительным ускорением (обозначается 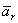 ). Из определения следует, что при вычислении
). Из определения следует, что при вычислении 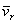 и
и 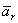 можно движение осей Oxyz во внимание не принимать (рассматривать их как неподвижные).
можно движение осей Oxyz во внимание не принимать (рассматривать их как неподвижные).
2. Движение, совершаемое подвижной системой отсчета Oxyz (и всеми неизменно связанными с нею точками пространства) по отношению к неподвижной системе 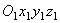 , является для точки М переносным движением.
, является для точки М переносным движением.
Скорость той неизменно связанной с подвижными осями Oxyz точки m, с которой в данный момент времени совпадает движущаяся точка М, называется переносной скоростью точки М в этот момент (обозначается 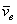 ), а ускорение этой точки m - переносным ускорением точки М (обозначается
), а ускорение этой точки m - переносным ускорением точки М (обозначается  ). Таким образом,
). Таким образом,
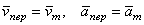 .
.
Если представить себе, что относительное движение точки происходит по поверхности (или внутри) твердого тела, с которым жестко связаны подвижные оси Oxyz, то переносной скоростью (или ускорением) точки М в данный момент времени будет скорость (или ускорение) той точки т тела, с которой в этот момент совпадает точка М.
3. Движение, совершаемое точкой по отношению к неподвижной системе отсчета 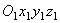 , называется абсолютным или сложным. Траектория CD этого движения называется абсолютной траекторией, скорость - абсолютной скоростью (обозначается
, называется абсолютным или сложным. Траектория CD этого движения называется абсолютной траекторией, скорость - абсолютной скоростью (обозначается 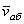 ) и ускорение - абсолютным ускорением (обозначается
) и ускорение - абсолютным ускорением (обозначается 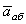 ).
).
В приведенном выше примере движение шара относительно палубы парохода будет относительным, а скорость - относительной скоростью шара; движение парохода по отношению к берегу будет для шара переносным движением, а скорость той точки палубы, которой в данный момент времени касается шар будет в этот момент его переносной скоростью; наконец, движение шара по отношению к берегу будет его абсолютным движением, а скорость - абсолютной скоростью шара.
При исследовании сложного движения точки полезно применять «Правило остановки». Для того, чтобы неподвижный наблюдатель увидел относительное движение точки, надо остановить переносное движение.
Тогда будет происходить только относительное движение. Относительное движение станет абсолютным. И наоборот, если остановить относительное движение, переносное станет абсолютным и неподвижный наблюдатель увидит только это переносное движение.
В последнем случае, при определении переносного движения точки, обнаруживается одно очень важное обстоятельство. Переносное движение точки зависит от того в какой момент будет остановлено относительное движение, от того, где точка находится на среде в этот момент. Так как, вообще говоря, все точки среды движутся по-разному. Поэтому логичнее определять переносное движение точки как абсолютное движение той точки среды, с которой совпадает в данный момент движущаяся точка.
Вопрос
Рис.32
Поэтому в механике вводится еще одна характеристика распределения масс - момент инерции. Моментом инерциитела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси
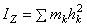
Из определения следует, что момент инерции тела (или системы) относительно любой оси является величиной положительной и не равной нулю.
Заметим также, что момент инерции тела – это геометрическая характеристика тела, не зависящая от его движения.
Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т.е. что осевой момент инерции является мерой инертности тела при вращательном движении.
Согласно формуле момент инерции тела равен сумме моментов инерции всех его частей относительно той же оси. Для одной материальной точки, находящейся на расстоянии h от оси,  .
.
Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси О z называется линейная величина  , определяемая равенством
, определяемая равенством
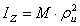 ,
,
где М - масса тела. Из определения следует, что радиус инерции геометрически равен расстоянию от оси О z той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.
В случае сплошного тела, разбивая его на элементарные части, найдем, что в пределе сумма, стоящая в равенстве 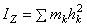 , обратится в интеграл. В результате, учитывая, что
, обратится в интеграл. В результате, учитывая, что 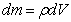 , где
, где 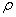 - плотность, а V- объем, получим
- плотность, а V- объем, получим
 или
или 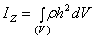
Интеграл здесь распространяется на весь объем V тела, а плотность 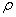 и расстояние h зависят от координат точек тела.
и расстояние h зависят от координат точек тела.
Моменты инерции некоторых однородных тел:
1.Тонкий однородный стержень длины l и массы М. Вычислим его момент инерции относительно оси А z, перпендикулярной к стержню и проходящей через его конец А (рис. 33).

Рис.33
Направим вдоль АВ координатную ось Ах. Тогда для любого элементарного отрезка длины dx величина h = x, а масса 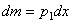 , где
, где 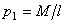 - масса единицы длины стержня. В результате
- масса единицы длины стержня. В результате
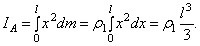
Заменяя здесь  его значением, найдем окончательно:
его значением, найдем окончательно:
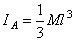
2. Тонкое круглое однородное кольцо радиуса R и массы М. Найдем его момент инерции относительно оси Cz, перпендикулярной плоскости кольца и проходящей через его центр (рис.34, а). Так как все точки кольца находятся от оси Cz на расстоянии hk = R, то

Следовательно, для кольца 
Очевидно, такой же результат получится для момента инерции тонкой цилиндрической оболочки массы М и радиуса R относительно ее оси.
3. Круглая однородная пластина или цилиндр радиуса R и массы М. Вычислим момент инерции круглой пластины относительно оси С z, перпендикулярной к пластине и проходящей через ее центр (см. рис.34, а). Для этого выделим элементарное кольцо радиуса r и ширины dr (рис.34, б).
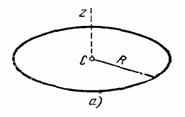
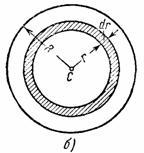
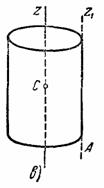
Рис.34
Площадь этого кольца равна 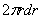 , а масса
, а масса 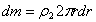 , где
, где 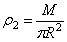 - масса единицы площади пластины. Тогда для выделенного элементарного кольца будет
- масса единицы площади пластины. Тогда для выделенного элементарного кольца будет
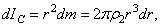
а для всей пластины  . Заменяя здесь
. Заменяя здесь 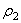 его значением, найдем окончательно
его значением, найдем окончательно 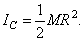
Такая же формула получится, очевидно, и для момента инерции 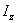 однородного круглого цилиндра массы М и радиуса R относительно его оси О z (риc.34, в).
однородного круглого цилиндра массы М и радиуса R относительно его оси О z (риc.34, в).
4. Прямоугольная пластина, конус, шар. Опуская выкладки, приведем формулы, определяющие моменты инерции следующих тел:
а) сплошная прямоугольная пластина массы М со сторонами АВ = а и BD = b (ось х направлена вдоль стороны AB, ось у - вдоль BD):

б) прямой сплошной круглый конус массы М с радиусом основания R (ось z направлена вдоль оси конуса):
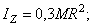
г) сплошной шар массы М и радиуса R (ось z направлена вдоль диаметра): 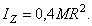
Рис.37
Оси x, y и z – главные центральные оси инерции, т.к. они являются осями симметрии.
Тогда 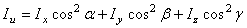 , где
, где 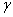 - угол между осями u и z; угол
- угол между осями u и z; угол 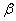 - угол между осями u и y, равный
- угол между осями u и y, равный 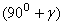 ; угол
; угол 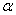 - угол между осями u и x, равный 90°. Поэтому
- угол между осями u и x, равный 90°. Поэтому
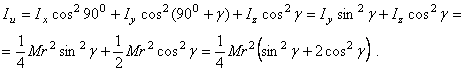
№21) Теорема об изменении главного момента количеств движения системы (теорема моментов).
Теорема моментов для одной материальной точки будет справедлива для каждой из точек системы. Следовательно, если рассмотреть точку системы с массой 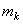 , имеющую скорость
, имеющую скорость  , то для нее будет
, то для нее будет
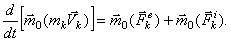
где 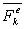 и
и 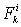 - равнодействующие всех внешних и внутренних сил, действующих на данную точку.
- равнодействующие всех внешних и внутренних сил, действующих на данную точку.
Составляя такие уравнения для всех точек системы и складывая их почленно, получим:
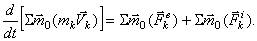
Но последняя сумма по свойству внутренних сил системы равна нулю. Тогда найдем окончательно:
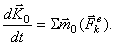
Полученное уравнение выражает следующую теорему моментов для системы: производнаяпо времени от главногомомента количеств движения системы относительно некоторого неподвижного центра, равна сумме моментов всех внешних сил системы относительно того же центра.
Проектируя обе части равенства на неподвижные оси Оху z, получим:

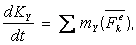

Уравнения выражают теорему моментов относительно любой неподвижной оси.
В кинематике было показано, что движение твердого тела в общем случае слагается из поступательного движения вместе с некоторым полюсом и вращательного движения вокруг этого полюса. Если за полюс выбрать центр масс, то поступательная часть движения тела может быть изучена с помощью теоремы о движении центра масс, а вращательная - с помощью теоремы моментов.
Практическая ценность теоремы моментов состоит еще в том, что она, аналогично теореме об изменении количества движения, позволяет при изучении вращательного движения системы исключать из рассмотрения все наперед неизвестные внутренние силы.
2. Теорема о моментах инерции твёрдого тела относительно параллельных осей.
Момент инерции твердого тела относительно некоторой оси равен моменту инерции тела относительно параллельной оси проходящей через его центр масс, сложенному с произведением массы тела на квадрат расстояния между осями. Допустим, что задана ось Oz1. Для доказательства теоремы проведём через центр масс тела С три взаимно перпендикулярные оси, из которых ось Сz параллельна заданной оси Oz1, а ось Су лежит в плоскости параллельных осей Сz и Oz1 (рис а, в). Обозначим d — расстояние между осями Cz и Oz1. для вычисления моментов инерции тела относительно осей Cz и Oz1 опустим из каждой точки Mi рассматриваемого тела перпендикуляры ri и hi на оси Cz и Oz1. Выразим длины этих перпендикуляров через координаты этих точек:
ri2 = xi2 + yi2, hi2 = xi2 + (yi — d)2 = xi2 + yi2 + d2 — 2yid = ri2 + d2 — 2yid. (a)
Определим моменты инерции тела относительно осей Cz и Oz1:
JCz = ∑ miri2, Jz1 = ∑ mihi2.
Применив зависимость (а): Jz1 = ∑ miri2 + ∑ mid2 — 2∑miyid. (в)
Здесь ∑ mi = m. — масса тела. Из формулы yc = ∑ miyi/m, получим:
∑ miyi = myc, так как yc = 0, то ∑miyi = 0. Подставляя это значение в равенство (в), получаем зависимость, установленную теоремой:
Jz1 = Jcz + md2. (г). Формула (г) показывает, что из совокупности паралельных осей ось, проходящая через центр масс тела, характеризуется наименьшим моментом инерции. Полярный момент тв. тела относительно центра масс: Jc = ½ * (Jcx + Jcy + Jcz). Отсюда следут, что ценр масс тела явл. полюсом, относительно которго полярный момент инерции тела имеет наименьшее возможное значение.
Воспользуемся формулой (г) для установления зависимости между радиусами инерции твёрдого тела icz и iz1относительно осей Cz и Oz1.
Jz1 = miz12, Jcz = micz2, тогда miz12 = mcz2 + md2, откуда iz12 = icz2 + d2.
3. Теорема об изменении количества движения механической системы.
Изменение количества движения мех. сис. за некотрый промежуток времени равно геометрической сумме импульсов внешних сил приложенных к системе за тотже промежуток времени.
K = ∑ mкυк; K = ∑ mкdrк/dt = d/dt * ∑mкrк = d/dt * mrc = mdrc/dt = mυc => K = mυc. Найдём призводную: dK/dt = d(mυc)/dt = mdυc/dt = mac Но из теоремы о движении ценра масс мех. сис. mac = RE = ∑ PкE; dK /dt = ∑ PкE. Проинтегрируем это выражение: ∫к1к2dK = ∫t1t2∑PкEdt;
k2-k1=∑SкE — ч.т.д.
вопрос Условия равновесия произвольной плоской системы сил
Для равновесия любой плоской системы сил необходимо и достаточно, чтобы выполнялись условия (4.2.5):
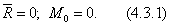
Записывая условия равновесия в аналитической форме, можно привести три их классических вида:
1. Основная форма условий равновесия:
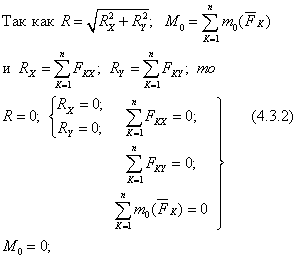
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций на оси координат были равны нулю и сумма моментов всех сил относительно центра О была равна нулю.
2. Вторая форма условий равновесия.
Для равновесия произвольной плоской системы необходимо и достаточно, чтобы сумма моментов относительно двух произвольно взятых точек тела была равна нулю и сумма проекций сил на одну из осей координат была равна нулю:
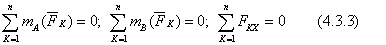
3. Уравнения трех моментов.
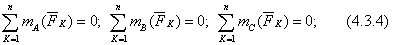
Дополнительное условие: А, В, С не лежат на одной прямой.



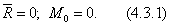
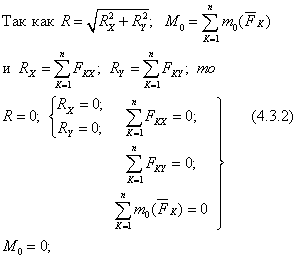
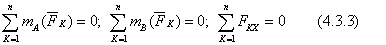
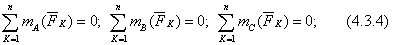
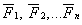 (рис.35
(рис.35  )
)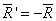 мы приведем систему сил
мы приведем систему сил 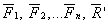 в равновесие и для нее будут выполняться условия (5.3.2). В частности для оси Ох:
в равновесие и для нее будут выполняться условия (5.3.2). В частности для оси Ох: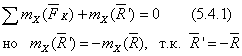
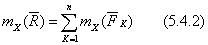

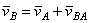 . Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор
. Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор 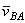 перпендикулярен АВ, находим
перпендикулярен АВ, находим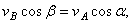
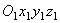 , которую называем основной или условно неподвижной (рис. 48). Каждая из этих систем отсчета связана, конечно, с определенным телом, на чертеже не показанным. Введем следующие определения.
, которую называем основной или условно неподвижной (рис. 48). Каждая из этих систем отсчета связана, конечно, с определенным телом, на чертеже не показанным. Введем следующие определения.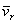 ), a ускорение - относительным ускорением (обозначается
), a ускорение - относительным ускорением (обозначается 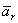 ). Из определения следует, что при вычислении
). Из определения следует, что при вычислении 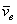 ), а ускорение этой точки m - переносным ускорением точки М (обозначается
), а ускорение этой точки m - переносным ускорением точки М (обозначается  ). Таким образом,
). Таким образом,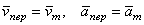 .
.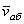 ) и ускорение - абсолютным ускорением (обозначается
) и ускорение - абсолютным ускорением (обозначается 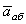 ).
).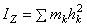
 .
. , определяемая равенством
, определяемая равенством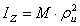 ,
,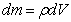 , где
, где 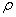 - плотность, а V- объем, получим
- плотность, а V- объем, получим или
или 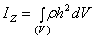

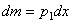 , где
, где 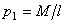 - масса единицы длины стержня. В результате
- масса единицы длины стержня. В результате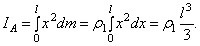
 его значением, найдем окончательно:
его значением, найдем окончательно: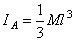





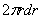 , а масса
, а масса 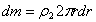 , где
, где 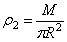 - масса единицы площади пластины. Тогда для выделенного элементарного кольца будет
- масса единицы площади пластины. Тогда для выделенного элементарного кольца будет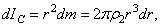
 . Заменяя здесь
. Заменяя здесь 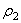 его значением, найдем окончательно
его значением, найдем окончательно 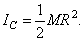
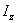 однородного круглого цилиндра массы М и радиуса R относительно его оси О z (риc.34, в).
однородного круглого цилиндра массы М и радиуса R относительно его оси О z (риc.34, в).
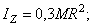
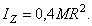
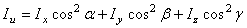 , где
, где 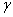 - угол между осями u и z; угол
- угол между осями u и z; угол 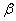 - угол между осями u и y, равный
- угол между осями u и y, равный 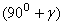 ; угол
; угол 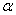 - угол между осями u и x, равный 90°. Поэтому
- угол между осями u и x, равный 90°. Поэтому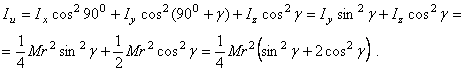
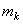 , имеющую скорость
, имеющую скорость  , то для нее будет
, то для нее будет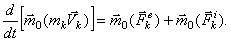
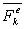 и
и 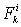 - равнодействующие всех внешних и внутренних сил, действующих на данную точку.
- равнодействующие всех внешних и внутренних сил, действующих на данную точку.