Практическая работа 4. Двойственные задачи линейного программирования. 33
Практическая работа 5. Транспортные задачи линейного программирования. Решение методом потенциалов. 53
Практическая работа 6. Матричные игры. Чистые и смешанные стратегии. Решение задач теории игр Графическое решение. 66
Практическая работа № 7. Доминирование строк и столбцов матрицы. Сведение матричной игры к задаче линейного программирования. 72
Практическая работа 8. Сетевая модель. Порядок и правила построения сетевых графиков. Анализ и оптимизация сетевого графика. 78
Литература: 92
Введение
Цель дисциплины – формирование обще-профессиональных компетенций по направлению подготовки 09.03.03 "Прикладная информатика" ОПК-2 (способностью анализировать социально-экономические задачи и процессы с применением методов системного анализа и математического моделирования), а также изучение основных понятий и методов исследования операций, возможностей и особенностей использования математических методов в решении экономических задач.
Теоретической и практической основой для изучения курса являются дисциплины «Математический анализ», «Линейная алгебра и аналитическая геометрия», «Теория систем и системный анализ».
Дисциплина «Исследование операций» является общим теоретическим и методологическим основанием для изучения последующих дисциплин:
"Имитационное моделирование экономических процессов", "Моделирование информационных систем в экономике","Научно-исследовательская работа".
В результате изучения дисциплины обучающийся должен знать:
- основные понятия и определения теории исследования операций;
- постановка задач линейного программирования;
- методы решения задач линейного программирования;
- двойственные задачи, их постановка и совместное решение;
- основные термины и определения теории игр, методы решения задач теории игр;
Уметь:
- проводить экономико-математический анализ на основе оптимальных решений;
- использовать методы решения задач линейного программирования;
- использовать графический метод решения задач линейного программирования;
- анализировать экономико-математические модели на чувствительность к изменению параметров;
Владеть:
- навыками экономико-математического анализ на основе оптимальных решений;
- навыками решения задач линейного программирования;
- навыками графический метод решения задач линейного программирования;
- навыками анализа экономико-математических моделей на чувствительность к изменению параметров.
Практическая работа 1. Задачи линейного программирования, примеры их постановки и графическое решение
Цель: Ознакомить студентов с методикой постановки задач линейного программирования и способом графического их решения.
В результате проработки темы студент должен научиться переводить словесное описание задачи в математическую постановку в виде линейных уравнений, неравенств, определять область допустимых решений и графически находить оптимальное решение задачи.
Актуальность темы: Постановка задач является ключевым моментомпри математическом моделировании. Графический метод решения – простейший для задач линейного программирования.
Теоретическая часть
На основе известных законов (природы, физики, экономики и других) составляются уравнения, неравенства или их системы, описывающие либо равновесие спроса и предложения, либо баланс материальных и денежных ресурсов, а также физические законы сохранения материи, энергии, вещества, соотношения денежного обмена и т. п. Составление этих математических задач как раз и является сутью математического моделирования, а результаты их решения описывают различные аспекты моделируемого явления.
Примеры постановки задач линейного программирования
Задача 1. (об ассортименте)
Для производства различных моделей А и В используется три вида сырья. На изготовление единицы изделия А требуется затратить сырья первого вида а1 = 12 кг, сырья второго вида а2 = 4 кг, сырья третьего вида а3 = 3кг. На изготовление единицы изделия В требуется затратить сырья первого вида b1 = 3 кг, сырья второго вида b2 = 5 кг, сырья третьего вида b3 =14 кг.
Производство обеспечено сырьем первого вида в количестве р1 = 264 кг, сырьем второго вида в количестве р2 = 136 кг, сырьем третьего вида в количестве р3 = 266 кг.
Прибыль от реализации единицы готового изделия А составит а = 6 руб., а изделия В: b = 4 руб. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
Постановка задачи
Процесс построения математической модели начинается с ответов на три вопроса:
1. Каковы переменные задачи? Их обозначаем 
2. Какие ограничения должны учитываться для переменных?
3. В чем состоит цель задачи, то есть что представляет собой целевая функция?
Рассмотрим процесс построения математической модели на примере нашей задачи. Оформим данные задачи в виде таблицы.
| Вид сырья
| Вид изделия
| Запасы сырья
|
| А
| В
|
| Первое
Второе
Третье
|
|
|
|
| Прибыль, руб.
|
|
|
|
Введем переменные.
Обозначим:  1 (ед.) – количество изделий А;
1 (ед.) – количество изделий А;
 2 (ед.) – количество изделий В;
2 (ед.) – количество изделий В;
U (руб.) – прибыль от реализации всей продукции.
Совокупность неизвестных ( 1;
1;  2) называется планом производства. Очевидно, должны соблюдаться условия неотрицательности:
2) называется планом производства. Очевидно, должны соблюдаться условия неотрицательности:
 1 ≥ 0,
1 ≥ 0,  2 ≥ 0.
2 ≥ 0.
Составим ограничения по сырью каждого вида. На изготовление  1 единиц изделий А расходуется 12∙
1 единиц изделий А расходуется 12∙  1 (кг) сырья первого вида, на изготовление
1 (кг) сырья первого вида, на изготовление  2 единиц изделий В расходуется 3 ∙
2 единиц изделий В расходуется 3 ∙  2 (кг) сырья первого вида. Полный расход сырья первого вида составит (12
2 (кг) сырья первого вида. Полный расход сырья первого вида составит (12  1 + 3
1 + 3  2) кг, и не должен превышать запасов этого сырья в количестве 264 кг, т. е. 12
2) кг, и не должен превышать запасов этого сырья в количестве 264 кг, т. е. 12  1 + +3
1 + +3  2 ≤ 264.
2 ≤ 264.
Аналогично для сырья второго вида 4  1 + 5
1 + 5  2 ≤ 136 и для сырья третьего вида 3
2 ≤ 136 и для сырья третьего вида 3  1 + 14
1 + 14  2 ≤ 266.
2 ≤ 266.
По условию задачи прибыль от реализации единицы изделия А составляет 6 руб., а следовательно, прибыль от реализации всех  1 единиц изделий А составит 6 ∙
1 единиц изделий А составит 6 ∙  1 руб., прибыль от реализации
1 руб., прибыль от реализации  2 единиц изделий В составит 4 ∙
2 единиц изделий В составит 4 ∙  2 руб.
2 руб.
Общая прибыль от реализации всех изделий U = (6  1 +4
1 +4  2) руб. U называется целевой функцией задачи. Ее значение должно быть максимальным, т. е. U = 6
2) руб. U называется целевой функцией задачи. Ее значение должно быть максимальным, т. е. U = 6  1 +4
1 +4  2 - > МАХ.
2 - > МАХ.
Система полученных линейных неравенств – ограничений по сырью вместе с условием неотрицательности и целевой функцией образует математическую модель задачи стандартного вида:
12  1 + 3
1 + 3  2 ≤ 264;
2 ≤ 264;
4  1 + 5
1 + 5  2≤ 136; (1)
2≤ 136; (1)
3  1 + 14
1 + 14  2 ≤ 266;
2 ≤ 266;
 1 ≥ 0
1 ≥ 0  2 ≥ 0;
2 ≥ 0;
U = 6  1 +4
1 +4  2 - > МАХ.
2 - > МАХ.
Полученная математическая модель (1) называется задачей линейного программирования (ЗЛП), т. к. линейны все неравенства системы ограничений и целевая функция U.
Допустимый план – это пара значений ( 1;
1;  2), удовлетворяющая системе ограничений и условиям неотрицательности.
2), удовлетворяющая системе ограничений и условиям неотрицательности.
Оптимальный план – это допустимый план, доставляющий максимум (или минимум) целевой функции U.
Если неравенства в модели (1) непротиворечивы, то имеется, вообще говоря, бесчисленное множество допустимых планов, из которых нужно выбрать оптимальный (наилучший).
Задача 2. (об использовании ресурсов, одна из задач планирования производства).
Для изготовления двух видов продукции  и
и  используют четыре вида ресурсов
используют четыре вида ресурсов  и
и  . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице (цифры условные).
. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице (цифры условные).
Таблица 1.
| Вид ресурса
| Запас ресурса
| Число единиц, затрачиваемых на изготовление единицы
продукции
|

| 
|

|
|
|
|

|
|
|
|

|
| −
|
|

|
|
| −
|
Прибыль, получаемая от единицы продукции  и
и  , − соответственно 2 и 3 руб.
, − соответственно 2 и 3 руб.
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.
Решение.
Составим экономико-математическую модель задачи.
Обозначим 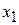 ,
,  − число единиц продукции соответственно
− число единиц продукции соответственно  и
и  , запланированных к производству. Для их изготовления (см. табл. 1) потребуется
, запланированных к производству. Для их изготовления (см. табл. 1) потребуется 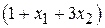 единиц ресурса
единиц ресурса  ,
,  единиц ресурса
единиц ресурса  ,
, 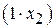 единиц ресурса
единиц ресурса  и
и  единиц ресурса
единиц ресурса  . Так как потребление ресурсов
. Так как потребление ресурсов  и
и  не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
 (2)
(2)
По смыслу задачи переменные
 . (3)
. (3)
Суммарная прибыль  составит
составит  руб. от реализации продукции
руб. от реализации продукции  и
и  руб. − от реализации продукции
руб. − от реализации продукции  , т.е.
, т.е.
 . (4)
. (4)
Итак, экономико-математическая модель задачи:
найти такой план выпуска продукции  , удовлетворяющий системе (2) и условию (3), при котором функция (4) принимает максимальное значение.
, удовлетворяющий системе (2) и условию (3), при котором функция (4) принимает максимальное значение.




 1 (ед.) – количество изделий А;
1 (ед.) – количество изделий А; и
и  используют четыре вида ресурсов
используют четыре вида ресурсов  и
и  . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице (цифры условные).
. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице (цифры условные).


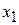 ,
,  − число единиц продукции соответственно
− число единиц продукции соответственно 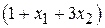 единиц ресурса
единиц ресурса  единиц ресурса
единиц ресурса  ,
, 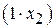 единиц ресурса
единиц ресурса  единиц ресурса
единиц ресурса  (2)
(2) . (3)
. (3) составит
составит  руб. от реализации продукции
руб. от реализации продукции  руб. − от реализации продукции
руб. − от реализации продукции  . (4)
. (4) , удовлетворяющий системе (2) и условию (3), при котором функция (4) принимает максимальное значение.
, удовлетворяющий системе (2) и условию (3), при котором функция (4) принимает максимальное значение.

