Цель: Ознакомить студентов с методикой постановки задач на основе алгебры матриц.
В результате проработки темы студент должен освоить основы линейной алгебры, уметь выполнять действия над алгебраическими объектами, использовать их при решении задач.
Актуальность темы: Математическое моделирование начинается с перевода словесного описания модели на язык математических формул.
Теоретическая часть
Исходной информацией при построении математической модели объекта служат данные о его назначении и условиях работы. Эта информация определяет цель моделирования и позволяет сформулировать требования к математической модели.
На основе известных законов (природы, физики, экономики и других) составляются уравнения, неравенства или их системы, описывающие либо равновесие спроса и предложения, либо баланс материальных и денежных ресурсов, а также физические законы сохранения материи, энергии, вещества, соотношения денежного обмена и т. п. Составление этих математических задач как раз и является сутью математического моделирования, а результаты их решения описывают различные аспекты моделируемого явления.
Постановка задачи при моделировании предполагает ответы на три вопроса:
1. Каковы переменные этой задачи, то есть что требуется в ней найти? Переменные мы вводим и обозначаем сами.
2. Какие ограничения должны быть наложены на переменные, согласно условиям задачи?
3. Какова цель задачи?
Пример простейшей модели планирования производства
Предприятие производит два вида продукции П1 и П2 (например, туфли и ботинки) и использует два вида сырья (кожу и резину) ежедневные запасы которых соответственно b1 и b2 условных единиц. Согласно технологии производства, аij количество i – го вида сырья идущего на изготовление единицы j – ой продукции (например,  - количество кожи, идущей на один ботинок). Требуется спланировать работу так, чтобы ежедневно использовать полностью запасы сырья.
- количество кожи, идущей на один ботинок). Требуется спланировать работу так, чтобы ежедневно использовать полностью запасы сырья.
В нашей задаче нужно определить количество  и
и  - продукции видов П1 и П2 соответственно. Можно сказать, что нужно найти вектор -план
- продукции видов П1 и П2 соответственно. Можно сказать, что нужно найти вектор -план  с координатами
с координатами  ,
,  . Для постановки задач часто удобно использовать балансовую таблицу (здесь - таблица 1), в которую можно вписать все данные и используемые переменные, причем информацию о технологии производства впишем в уголки ячеек.
. Для постановки задач часто удобно использовать балансовую таблицу (здесь - таблица 1), в которую можно вписать все данные и используемые переменные, причем информацию о технологии производства впишем в уголки ячеек.
Таблица 1 Балансовая таблица данных задачи
 Продукт
Сырье Продукт
Сырье
| П1
| П2
| Запасы
сырья
|
| А
| 

| 

| 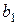
|
| Б
| 

| 

| 
|
Из таблицы легко вытекают балансовые соотношения по расходу сырья (ограничения):
 (1)
(1)
Получилась система двух уравнений с двумя неизвестными  и
и  . В данной задаче целью является полное использование сырья, поэтому строгие равенства в балансовых соотношениях служат как ограничениями, так и целевой характеристикой задачи.
. В данной задаче целью является полное использование сырья, поэтому строгие равенства в балансовых соотношениях служат как ограничениями, так и целевой характеристикой задачи.
Решая систему школьным методом алгебраического сложения, получим:

или  ; аналогично
; аналогично  (2)
(2)
Очевидно, что эти формулы легче запомнить если ввести в рассмотрение матрицу коэффициентов, т.е. таблицу чисел:
 (3)
(3)
(в данной задаче она является технологической матрицей), где первый индекс показывает номер строки, второй – номер столбца, на которых находится элемент. В числителе и знаменателе формул (2) стоят числа, обозначим их буквами D1, D2, D, так что
 ;
;  , (4)
, (4)
где 
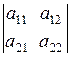 (5)
(5)
- число, которое находится как разность произведений чисел, лежащих на главной и побочной диагоналях определителя (5), полученного из матрицы (3). Аналогично вычисляются определители
 ;
;  (6)
(6)
Заметим, что формулы (4) представляют собой правило Крамера для решения системы двух линейных алгебраических уравнений с двумя неизвестными.
Таким образом, при описании поставленной проблемы средствами математики мы использовали в этой задаче разные математические формы обработки одной и той же информации: систему уравнений, матрицу, определители, вектор. Это родственные математические понятия, но каждое имеет свои особенности и правила преобразований, используя которые, можно найти наиболее простой путь решения задачи.
Задание: Повторить из курса математики темы: определители, матрицы, системы линейных алгебраических уравнений.
Задание к практическому занятию:
Задания выполняются в соотвктсвии со своим вариантом.
Базовый уровень:
Вычислить определители:
1.1. 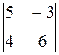 .
1.4. .
1.4.  .
1.7. .
1.7.  . .
| 1.2.  .
1.5. .
1.5.  .
1.8. .
1.8.  . .
| 1.3.  .
1.6. .
1.6.  .
1.9. .
1.9.  . .
|
1.10.  . .
| 1.11.  . .
|
1.12.  . .
| 1.13.  . .
|
1.14.  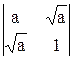 . .
| 1.15.  . .
|
1.16.  . .
| 1.17.  . .
|
1.18. 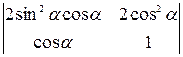 . .
|
1.19.  . .
| 1.20.  . .
|
| | | | |
Вычислить определители, предварительно упростив их:
1.21. 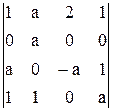 . .
| 1.22.  . .
|
1.23.  . .
| 1.24. 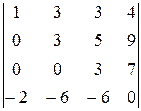 . .
|
1.25.  . .
| 1.26.  . .
|
1.27.  . .
| 1.28. 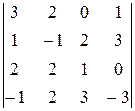 . .
|
1.29.  . .
| 1.30.  . .
|
Решить уравнения и выполнить проверку подстановкой корней в определитель:
1.31.  =0. =0.
| 1.32.  =0. =0.
|
1.33.  =0. =0.
| 1.34.  =0. =0.
|
1.35.  =0. =0.
| 1.36.  =0. =0.
|
1.37.  =0. =0.
| 1.38.  =0. =0.
|
1.39.  =0. =0.
| 1.40.  =0. =0.
|
Выполнить действия над матрицами:
1.41. C = 2A + B, где A = 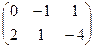 , B =
, B =  .
.
1.42. C = A · B, где A =  , B =
, B =  .
.
| 1.43. D = (2A + B) · C, где
A = (4 0 –2 3 1),
B = (1 –1 6 8 0),
|  . .
|
1.44. D = A · B · C, где
A =  ; B =
; B =  ; C =
; C =  ;
;
1.45. D = A2, где A =  ;
;
1.46. D = A3, где A =  ;
;
1.47. D = A4, где A =  ;
;
Найти f(A):
1.48. f(x) = 3x2 – 4, A = 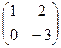 ;
;
1.49. f(x) = x2 + x, A = 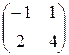 ;
;
1.50. f(x) = 3x2 – 2x + 1, A =  ;
;
Найти транспонированные и обратные для следующих матриц:
1.51.  ; ;
| 1.52.  ; ;
|
1.53.  ; ;
| 1.54.  ; ;
|
1.55. 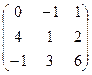 ; ;
| 1.56.  ; ;
|
1.57.  ; ;
| 1.58. 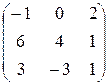 ; ;
|
1.59.  ; ;
| 1.60.  . .
|
Решить матричные уравнения:
1.61.  · X =
· X =  . 1.62. X ·
. 1.62. X ·  =
=  .
.
1.63. X ·  =
= 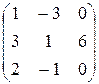 .
.
1.64. X ·  =
=  .
.
Доказать равенства:
| 1.65. a) (AT)T = A;
| b) (A + B)T = AT + BT;
|
| 1.66. (A · B)T = BT · AT ;
| 1.67. (α · A)–1 =  A–1; A–1;
|
| 1.68. (A–1)T = (AT)–1;
| 1.69. (A · B)–1 = B–1 · A–1.
|
1.70. Вычислить: A · AT и AT · A для A =  .
.
Ранг матрицы
Если выделить в матрице из m × n элементов k строк и k столбцов, где k – число меньшее или равное меньшему из чисел m и n, то определитель порядка k, составленный из элементов выделенных k строк и k олбцов, называется минором, порожденным матрицей A.
Базисным минором называется всякий отличный от нуля определитель, порядок которого равен рангу матрицы.
Методы нахождения ранга матрицы:
1. Метод единиц и нулей. Путем элементарных преобразований матрицу приводим к виду, когда каждый ее ряд содержит только нули и одну единицу. Число оставшихся единиц и определяет ранг исходной матрицы.
2. Метод окаймляющих миноров. Минор Mk+1 порядка k + 1, содержащий в себе минор Mk порядка k, называется окаймляющим минором Mk. Если матрица A имеет минор Mk ≠ 0, а все окаймляющие его миноры Mk+1 = 0, то ранг матрицы равен k. (rang A = k).
Пример
Найти ранг матрицы методом окаймляющих миноров.
A =  M2 =
M2 =  = –8 + 20 = 12 ≠ 0.
= –8 + 20 = 12 ≠ 0.
Для M2 окаймляющими будут:
 = 0,
= 0, 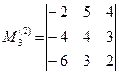 = 0. М
= 0. М
Поэтому rang A = 2.
Задание к практическому занятию:
Задания выполняются в соответсвии со своим вариантом.
Базовый уровень:
Найти ранг матрицы:
1.71.  . .
| 1.72.  . .
|
1.73.  . .
| 1.74.  . .
|
1.75.  . .
| 1.76.  . .
|
1.77.  . .
| 1.78.  . .
|
1.79.  . .
| 1.80.  . .
|



 - количество кожи, идущей на один ботинок). Требуется спланировать работу так, чтобы ежедневно использовать полностью запасы сырья.
- количество кожи, идущей на один ботинок). Требуется спланировать работу так, чтобы ежедневно использовать полностью запасы сырья. и
и  - продукции видов П1 и П2 соответственно. Можно сказать, что нужно найти вектор -план
- продукции видов П1 и П2 соответственно. Можно сказать, что нужно найти вектор -план  с координатами
с координатами  Продукт
Сырье
Продукт
Сырье




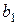





 (1)
(1)
 ; аналогично
; аналогично  (2)
(2) (3)
(3) ;
;  , (4)
, (4)
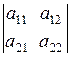 (5)
(5) ;
;  (6)
(6)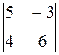 .
1.4.
.
1.4.  .
1.7.
.
1.7.  .
.
 .
1.5.
.
1.5.  .
1.8.
.
1.8.  .
.
 .
1.6.
.
1.6.  .
1.9.
.
1.9.  .
.
 .
.
 .
.
 .
.
 .
.

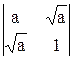 .
.
 .
.
 .
.
 .
.
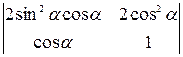 .
.
 .
.
 .
.
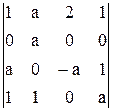 .
.
 .
.
 .
.
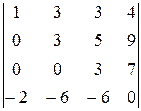 .
.
 .
.
 .
.
 .
.
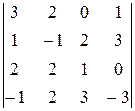 .
.
 .
.
 .
.
 =0.
=0.
 =0.
=0.
 =0.
=0.
 =0.
=0.
 =0.
=0.
 =0.
=0.
 =0.
=0.
 =0.
=0.
 =0.
=0.
 =0.
=0.
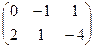 , B =
, B =  .
. , B =
, B =  .
. .
.
 ; B =
; B =  ; C =
; C =  ;
; ;
; ;
; ;
;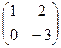 ;
;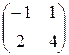 ;
; ;
; ;
;
 ;
;
 ;
;
 ;
;
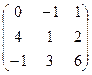 ;
;
 ;
;
 ;
;
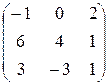 ;
;
 ;
;
 .
.
 · X =
· X =  . 1.62. X ·
. 1.62. X ·  =
=  .
. =
= 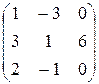 .
. =
=  .
. A–1;
A–1;
 .
. M2 =
M2 =  = –8 + 20 = 12 ≠ 0.
= –8 + 20 = 12 ≠ 0. = 0,
= 0, 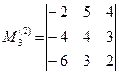 = 0. М
= 0. М .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.

