Косвенные измерения предполагают наличие известной функциональной связи между искомой величиной y и независимыми аргументами, которые могут быть найдены прямыми измерениям

| (8)
|
Очевидно, погрешность в оценке y зависит от погрешности при измерении аргументов. При этом могут иметь место два случая: аргументы взаимонезависимы и взаимозависимы. Для независимых аргументов абсолютная погрешность Δy искомой величины близка к понятию полного дифференциала функции (8)
Запишем выражение для полного дифференциала функции y.

По определению полный дифференциал функции – это приращение функции, вызванное малым приращением ее аргументов.
Учитывая, что погрешность измерения аргументов всегда являются малыми величинами по сравнению с номинальными значениями аргументов можно заменить дифференциалы аргументов  на границы абсолютных погрешностей аргументов
на границы абсолютных погрешностей аргументов  , а дифференциал dy на абсолютную погрешность результата измерений
, а дифференциал dy на абсолютную погрешность результата измерений 

| (9)
|
В полученную формулу входят частные производные 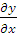 , которые могут быть как положительными, так и отрицательными величинами. Опыт показывает, что при увеличении источников погрешностей (аргументы функции х1; х2…хn) результирующая погрешность, т.е. погрешность косвенного измерения, всегда увеличивается в связи с этим абсолютную погрешность косвенного измерения Δy определяют по формуле
, которые могут быть как положительными, так и отрицательными величинами. Опыт показывает, что при увеличении источников погрешностей (аргументы функции х1; х2…хn) результирующая погрешность, т.е. погрешность косвенного измерения, всегда увеличивается в связи с этим абсолютную погрешность косвенного измерения Δy определяют по формуле
 = = 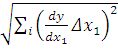
| (10)
|
По аналогичной формуле можно определить и среднеквадратичную погрешность косвенного измерения σу, поскольку ее размерность так же как и для абсолютной погрешности  совпадает с размерностью измеряемой величины
совпадает с размерностью измеряемой величины
 = = 
| (11)
|
Применяя формулу (9), получим несколько простых правил оценивания, т.е. нахождения приближенного значения погрешности косвенного измерения [2 c 53].
Правило1. Погрешности в суммах или разностях. Если 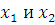 измерены с погрешностями
измерены с погрешностями  и измеренные значения используются для вычисления суммы или разности
и измеренные значения используются для вычисления суммы или разности  , то при нахождении погрешности косвенного измерения
, то при нахождении погрешности косвенного измерения  суммируются абсолютные погрешности величин
суммируются абсолютные погрешности величин  и
и  без учёта их знака
без учёта их знака  ,
,
Правило 2. Погрешности в произведениях и частных. Если измеренные значения 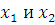 используются для вычисления
используются для вычисления  или
или  то суммируются относительные погрешности
то суммируются относительные погрешности  , где
, где  .
.
Если нужно найти абсолютную погрешность  , то она найдется по формуле
, то она найдется по формуле

Правило 3. Измеренная величина умножается на постоянное число. Если x используется для вычисления произведения y=B  x, в котором В не имеет погрешности, то
x, в котором В не имеет погрешности, то  Или для абсолютной погрешности
Или для абсолютной погрешности  .
.
Правило 4. Возведение в степень. Если x используется для вычисления степени  , то
, то  Или для абсолютных погрешностей
Или для абсолютных погрешностей 
Правило 5. Погрешность в произвольной функции одной переменной. Если x используется для вычисления функции y=f(x), то  . Или для абсолютных погрешностей
. Или для абсолютных погрешностей  .
.
Вывод этих правил не приводится и может быть легко сделан самостоятельно. Использование правил позволяет получить оценку предельной погрешности косвенного измерения при числе аргументов n<5.
Пример. Производится косвенное измерение мощности рассеиваемой на резисторе сопротивлением R при протекании по нему тока I.Так как  , то применяя правило 2 и 4, получим
, то применяя правило 2 и 4, получим  По определению
По определению  . Тогда для абсолютной погрешностей косвенного измерения мощности получим
. Тогда для абсолютной погрешностей косвенного измерения мощности получим  Причем
Причем  могут быть найдены по классам точности амперметра и омметра.
могут быть найдены по классам точности амперметра и омметра.







 на границы абсолютных погрешностей аргументов
на границы абсолютных погрешностей аргументов  , а дифференциал dy на абсолютную погрешность результата измерений
, а дифференциал dy на абсолютную погрешность результата измерений 

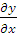 , которые могут быть как положительными, так и отрицательными величинами. Опыт показывает, что при увеличении источников погрешностей (аргументы функции х1; х2…хn) результирующая погрешность, т.е. погрешность косвенного измерения, всегда увеличивается в связи с этим абсолютную погрешность косвенного измерения Δy определяют по формуле
, которые могут быть как положительными, так и отрицательными величинами. Опыт показывает, что при увеличении источников погрешностей (аргументы функции х1; х2…хn) результирующая погрешность, т.е. погрешность косвенного измерения, всегда увеличивается в связи с этим абсолютную погрешность косвенного измерения Δy определяют по формуле =
= 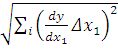
 =
= 
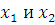 измерены с погрешностями
измерены с погрешностями  и измеренные значения используются для вычисления суммы или разности
и измеренные значения используются для вычисления суммы или разности  , то при нахождении погрешности косвенного измерения
, то при нахождении погрешности косвенного измерения  и
и  без учёта их знака
без учёта их знака  ,
, или
или  то суммируются относительные погрешности
то суммируются относительные погрешности  , где
, где  .
.
 x, в котором В не имеет погрешности, то
x, в котором В не имеет погрешности, то  Или для абсолютной погрешности
Или для абсолютной погрешности  .
. , то
, то  Или для абсолютных погрешностей
Или для абсолютных погрешностей 
 . Или для абсолютных погрешностей
. Или для абсолютных погрешностей  .
. , то применяя правило 2 и 4, получим
, то применяя правило 2 и 4, получим  По определению
По определению  . Тогда для абсолютной погрешностей косвенного измерения мощности получим
. Тогда для абсолютной погрешностей косвенного измерения мощности получим  Причем
Причем  могут быть найдены по классам точности амперметра и омметра.
могут быть найдены по классам точности амперметра и омметра.


