Линейное векторное метрическое нормированное пространство

3.1. Понятия и определения

 

Говорят, что множество имеет структуру, если между элементами множества установлены определенные соотношения. Множество, наделенное структурой, называют пространством.

Пусть X – произвольное множество. Свяжем с каждой парой элементов из X некоторое вещественное неотрицательное число d³0. Это число называют расстоянием или метрикой в X, если для любых x, y, zÎX оно удовлетворяет следующим трем аксиомам:

1) аксиома идентичности: d(x, y)=0 тогда и только тогда, когда x=y (аксиома идентичности);

2) аксиома симметрии: d(x, y)=d(y, x);

3) аксиома треугольника: для любой тройки x, y, zÎX имеет место d(x, y)£d(x, y)+d(y, z).

Метрическим пространством называют пару (X, d), то есть множество X с определенной на нем метрикой d. Элементы множества X называют точками метрического пространства (X, d).

Метрическое пространство называется линейным, если оно удовлетворяет следующим условиям:

1) каждой паре элементов x, yÎX однозначно определен третий элемент zÎX, называемый их суммой и обозначаемый x+y, причем

x+y=y+x (коммутативность);

x+(y+v)=(x+y)+v (ассоциативность);

в X существует такой элемент 0, что x+0=x для всех xÎX (существование нуля);

2) для любого числа a и любого элемента xÎX определен элемент axÎX, причем

(a+b)x=ax+bx; a(x+y)=ax+ay.

Условия 1 и 2 называют условиями аддитивности и однородности линейного пространства. Множества, элементы которых допускают выполнение операций сложения и умножения на скаляр, весьма разнообразны. Однако в дальнейшим сосредоточим свое внимание на линейных пространствах, элементами которых являются векторы или вектор-столбцы. Такое пространство называется векторным пространством.

Совокупность векторов  называется линейно-независимой, если существуют действительные числа k1, k2,…, kn, среди которых хотя бы одно не равнялось нулю, такие, что выполняется условие

Чтобы определить линейную зависимость или независимость совокупности векторов, можно использовать несколько способов.

1) Квадратная матрица называется особенной, если ее строки или столбцы линейно-зависимы. В этом случае det A=0.

2) Правило вырожденности Сильвестра. Дефект произведения двух матриц не меньше дефекта каждой из матриц и не выше суммы дефектов матриц.

3) Определитель Грама. Определитель Грама для системы векторов строится в предположении, что выполняется соотношение

Записывая последовательно скалярные произведения xi и обеих частей этого уравнения, получим систему уравнений

Система однородных уравнений имеет нетривиальное решение для ki только в том случае, если определитель матрицы с коэффициентами [<xi, xj>] равен нулю. Этот определитель называется определителем Грама и равен

 

Следовательно, система векторов линейно независима тогда и только тогда, когда определитель Грама для этой системы векторов равен нулю. Отметим, что в случае ортогогальных векторов определитель Грама является диагональным определителем.

Базисом называется упорядоченное множество линейно-независимых векторов. Базисов в конкретном векторном пространстве может быть бесконечно много. Однако число векторов в базисе всегда меньше или равно определенному значению. Максимальное число линейно-независимых векторов в данном векторном пространстве называется размерностью данного векторного пространства.

Любой вектор векторного пространства можно разложить по базису этого пространства и представить в виде:

,где – базисные векторы пространства, а коэффициенты k1, k2,…, kn называются координатами данного вектора в базисе =

Линейное пространство называют нормированным линейным пространством, если для каждого xÎX существует неотрицательное число ||x||, называемое нормой x, которое удовлетворяет следующим условиям:

||x||=0 тогда и только тогда, когда x=0;

||ax||=|a|×||x||;

||x+y||£||x||+||y||.

Нетрудно установить, что величина ||x–y|| обладает всеми свойствами расстояния d(x, y) в метрическом пространстве.

3.2. Линейное преобразование

 

Преобразованием линейного n-мерного пространства X называют оператор A, отображающий это пространство в m-мерное пространство Y:

A: X®Y.

Таким образом, преобразование A ставит в соответствие каждому вектору x пространства X вектор

y=Ax

пространства Y. В частном случае может быть Y=X. При этом преобразование A ставит в соответствие каждому вектору x пространства X вектор Ax того же самого пространства.

Преобразование A называют линейным, если выполняется условие

A(k1x1+k2x2)=k1 Ax1 + k2 Ax2.

Это условие будет выполняться, если между компонентами x(j) и y(i) векторов x и y имеется линейная зависимость вида

,

где aij – произвольные числа. Совокупность чисел aij, i=1, 2,…, m; j=1, 2, …, n образует матрицу A=[aij], которую называют матрицей линейного преобразования.

Среди линейных преобразований линейного пространства особую роль играют два:

1. Нулевое преобразование, ставящее в соответствие каждому вектору нулевой вектор o: Ox=o.

2. Единичное преобразование, ставящее в соответствие каждому вектору x тот же самый вектор: Ix=x.

Подпространство

 

Рассмотрим произвольное конечное множество точек S={x1, …, xm} линейного пространства X. Множество

при всевозможных ai также представляет собой линейное пространство, являющееся подмножеством линейного пространства X и называемое линейным подпространством.

4. Матричные преобразования

 

Матрица B эквивалентна матрице А в том случае, если существуют такие две неособенные матрицы P и Q, что

B=PAQ.

 

4.1. Преобразовани е подобия

 

Рассмотрим линейное преобразование

y=Ax,

где x и y определяются в n-мерном пространстве с базисом zi. Предположим теперь, что требуется перейти от данного базиса к системе векторов wi. В этом состоит общая проблема преобразования координат. Пусть x и y соответственно переходят в новом базисе в координаты x’ и y’. Так как для zi и wi составляют два базисы в n-мерном пространстве, то должна существовать такая неособенная матрица P, что

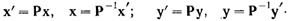
Найдем связь между y’ и x’ в новой системе координат. Для этого умножим слева обе части этого уравнения на P и получим Py=Pax. Из уравнения выше следует, что

или

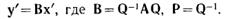
Матрица B, связывающая в новой системе координат x’ и y’, получается из A на основе преобразования подобия.

Преобразования подобия обладают важными свойствами:

1. Если матрица в одном базисе невырождена, то и в другом базисе она будет невырождена.

2. Определители, равно как и следы подобных матриц равны.

4.2. Ортогональное преобразование

Рассмотрим линейное преобразование

x=Qx’, P-1=Q,

где вектор x определяется в ортогональной системе координат. Если новая система координат также ортогональна, то длина вектора x’ в новой системе координат должна совпадать с длиной вектора x в первоначальной системе координат. Следовательно

<x, x>=<x’, x’>.

Выражая это соотношение посредством матрицы Q, имеем

Для этого необходимо, чтобы QT=Q-1.

Следовательно, при переходе от одного ортогонального базиса к другому матрица преобразования Q, ставящая в соответствие вектору в первоначальной системе координат вектор в новой системе координат, должна удовлетворят условию QT=Q-1. Данное преобразование называют ортогональным преобразованием. Матрица Q называется ортогональной матрицей. Ортогональное преобразование является частным случаем преобразования подобия. Оно оставляет неизменными длины и углы.

Из условия QT=Q-1 как следствие вытекает

|QT| |Q| = 1 или |Q| = ±1.

Знак минус в определителе означает, что ортогональное преобразование можно получить путем вращения или отражения. Косинусы углов между осью i' и осями 1, 2, …, n обозначаются соответственно элементами матрицы Q. Эти величины называются направляющими косинусами или направлениями новых осей по отношению к старым.

 

4.3. Конгруэнтное преобразование

 

Две матрицы называются конгруэнтными, если существует неособенная матрица Q, удовлетворяющая равенству

B=QTAQ.